基于负荷密度指标法的现代城镇电力负荷预测

徐亚玲，黄民德

(天津城建大学 控制与机械工程学院，天津 300384)

基于负荷密度指标法的现代城镇电力负荷预测

徐亚玲，黄民德

(天津城建大学 控制与机械工程学院，天津 300384)

安全、稳定、充裕的电力网络是现代城镇发展的基础．做好电网规划，首先要进行电力负荷预测．以往负荷密度指标的选取通常采用简单类比和经验判断得到，难以满足精度要求．通过引入模糊贴近度理论，使负荷密度指标的选取更科学精准，并以安徽省某现代城镇电力负荷预测为例，得到负荷密度指标值．实例表明，该方法结构合理，思路清晰，实用性较强．

电力网络；电力负荷预测；负荷密度指标；模糊贴近度

电力是城市发展的基础．随着中国城镇化进程的持续推进，城镇经济高速发展，越来越多的小城镇正向着现代化城镇迈进．安全、稳定、充裕的电力网络是现代城镇发展的基础，而做好电网供电规划，首先就要进行电力负荷预测．合理且精确的负荷预测可以有效避免资源浪费，提高电力系统的经济效益是电网规划成功的必要前提．另外，城市的供电规模、变电站(所)的容量、输电线路的输电能力等均依据电力负荷预测结果来确定．如果变电站和输电线路的容量选择过大，将造成设备的积压和浪费；反之，如果容量选择过小，则不能满足城市生产、生活的需要，阻碍城市各项事业的发展[1-3]．

负荷预测的方法很多，国内外学术界和工程界对电力负荷特性方面的研究颇多，取得了诸多重大成果．目前常用的方法有经验技术与经典技术、趋势外推技术、回归模型技术、其他预测技术等[4]．肖白等[5]提出了基于元胞历史负荷数据的负荷密度指标法，但该方法属于自上而下的空间负荷预测，需要大量历史数据，且适用于土地规划不明确的地块，在我国城网规划中成功应用的案例并不多见；孙威和杨修宇[6-7]提出了基于负荷密度指标法的配电网空间负荷预测方法，解决了对无历史数据的、无法依靠时间序列进行新城区空间负荷预测的问题；朱前进[8]在文献[6-7]的基础上引入模糊贴近度理论，加入了区域详细用地规划，使负荷的分类更加精细，并建立了影响因素的隶属函数，通过求取贴近度值，判断负荷密度指标范围，使之更加科学和精确．

但是，上述方法在构造单个影响因素对样本的隶属函数时缺乏科学依据，对标准样本的确定界定不清，数据陈旧，不能让人很好理解．由此，通过采用加权贴近度公式，计算不同等级标准样本和待测区样本对低水平样本的贴近度，以岭形分布的中间分布函数做隶属函数，用变异系数法确定各影响因素权重，从而提高预测的准确性和科学性．

1 模糊贴近度理论

模糊贴近度是用来反映两个模糊集合A与B的贴近程度的度量．其定义为：设论域为U，满足U={u1,u2,u3,…,un}，集合A和B是U上的两个模糊子集，若A与B的映射n(A,B)满足：①0≤n(A,B)≤1；②n(A,B)=n(B,A)；③n(A,A)=1,n(φ,U)=0；④A⊆B⊆C⇒n(A,C)≤n(A,B)∧n(B,C),则称n(A,B)为模糊集合A与B的贴近度．

贴近度计算公式有多种，在实际工程中，针对不同问题有不同的具体计算方法，需要根据模糊集合的特点，选择合适的贴近度计算公式．常用的贴近度公式如下．

(1)距离法确定贴近度．n(A,B)=1-cda(A,B)，其中：a、c为参数；称为闵科夫斯基距离，(p≥1)；当p＝1时，d(A,B)称为海明距离；当p＝2时，d(A,B)称为欧式距离．

(2)最大最小贴近度．

(3)最小平均贴近度．

(4)加权贴近度．

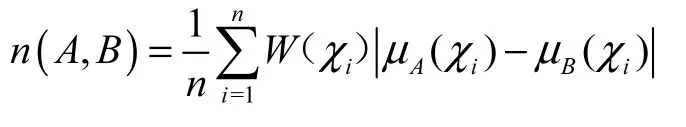
模糊贴近度理论是以模糊数学为基础，将模糊综合评判与贴近度公式结合，按照一定标准对某一系统进行综合评判．考虑被评对象的各种有关因素，将影响因素进行解析，并量化处理，最终得到贴近度结果．再根据贴近度结果得到取值范围．

2 负荷密度指标的选取

精细的负荷分类可以提高预测的准确性．将负荷类型按性质细分为15类：居住用地、行政办公用地、金融商业用地、文化娱乐用地、商业休闲用地、医疗卫生用地、教育科研用地、商住用地、工业用地、仓储用地、对外交通用地、市政用地、城市绿地用地、道路广场用地和水域．图1为该区域用地性质划分及编号图．针对每一类性质用地的负荷密度指标大小，按精确程度分为低、较低、中、较高、高5类，以满足模型辨别精确要求．

图1 用地性质划分及编号

假设某被评对象为集合X，X的取值区间不确定，故为模糊集合．模糊集X的n个影响因素构成影响因素集U＝{μ1,μ2,…,μn}；对模糊集X进行评判，构造评语集V＝{ν1,ν2,…,νm}＝{低，较低，中，较高，高}．标准样本集A的选取须满足贴近度的单调性原则，故选择低水平或高水平样本两种边缘情况作为基准较为合适．在各标准样本中，低水平样本比高水平样本的数据来源更广泛、更稳定，故本文采用低水平样本作为标准样本集A．

对低水平样本的n个影响因素构建一个隶属度为1的隶属函数，表示为，式中，表示影响因素i对样本的完全隶属度，且则模糊集X对样本的隶属度必定落在[0,1]区间内，且，式中，表示影响因素i对低水平样本的隶属度，且

通过模糊贴近度理论确定负荷密度指标的流程如图2所示．

3 算例分析

以安徽省凤台县城市规划中的居住用地负荷密度指标的选取为例，阐述引入模糊贴近度理论求取负荷密度指标的过程．

3.1 构造标准样本集和标准样本指标集

根据GB50293—1999《城市电力规划规范》[9]规定，居住用地用电指标为100～400,kW/hm2．由于各城市发展程度不同，故居民生活水平相差较大．调研整理部分参考样本住宅负荷密度指标，并结合城市规划预期，初步将居住用地负荷密度指标确定为200～300,kW/hm2．将样本均分成5份，采用低水平样本为标准样本，则标准样本集为A＝{200～220,kW/ hm2}．

调查统计表明，影响居住用地负荷密度指标的因素有地理位置、地理环境、占地面积、建筑面积、建筑功能与结构、区域经济发展水平、人均GDP值、城市定位、地区最高温度等．通过对多地区住宅样本和凤台县历年用电量数据分析，确定4个因素为主要影响因素：①城市定位1μ；②地理位置2μ；③人均GDP值3μ；④地区最高温度4μ．由此得到因素集U＝{1μ，2μ，3μ，4μ}．取每类样本的评价因素几何平均值构造5级标准样本指标表，见表1．

表1 5级标准样本指标

根据负荷预测统计数据以及凤台县城市总体概况、气候特点、地形地貌特征等相关资料，分析得到μ1-μ4的量化处理后数据分别为72，0.7，2,300美元，38.1,℃．

3.2 构造隶属函数，确定各影响因素权重

以μ4为例，建立“地区最高温度”对标准样本A的隶属函数，通过“参照函数法”作出其大致曲线图，发现曲线与岭形分布的中间型函数曲线十分相似，故选择岭形分布的中间型函数作为“地区最高温度”的隶属函数．岭形分布的中间型函数为

根据各地区负荷预测统计数据，得到地区最高温度的最低值为30.2,℃，最高值为42.1,℃，几何平均值为37.5,℃，即a1＝30.2，a2＝37.5，a3＝42.1，代入方程(1)得

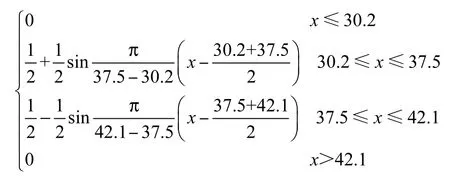
将μ4的量化数据38.1,℃(即x＝38.1)代入得到A(μ4)=0.5101，即为影响因素μ4对标准样本A(低水平样本)的隶属度．

同理可以得到影响因素μ1、μ2、μ3对标准样本A的隶属度分别为0.111,2、0.172,4、0.206,3．

3.3 计算贴近度，确定模糊集X的最终范围

本例中模糊集X和标准样本A的贴近度与模糊距离有关，距离越小，说明两个集合越贴近，其贴近度值就越大．故采用距离法中的海明贴近距离公式求取贴近度；同时考虑各影响因素的权重，进行加权处理，用变异系数法确定各影响因素权重．

假设影响因素iμ的变异系数为iδ，则有：，其中，D表示第i个影响因素的均方差；表示第i个影响因素的均值．

计算得到影响因素1μ、2μ、3μ、4μ的权重值(归一化后)分别为0.33、0.12、0.36、0.19．

则模糊集X对标准样本A的贴近度为

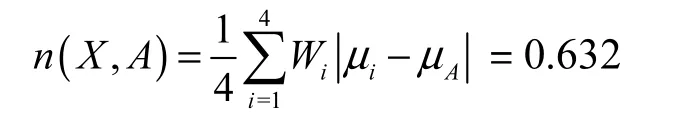
贴近度大小与归属等级划分如表2所示．

表2 贴近度大小与归属等级划分

由表2可知，模糊集X落在较低等级上，由此得到模糊集X的较为精确的取值范围，即居住用地负荷密度指标为220～240,kW/hm2，满足实际工程要求．

4 结 语

通过采用加权贴近度公式和岭形分布的中间分布函数做隶属函数，能较好地解决模糊贴近度理论求取负荷密度指标的问题，使其分辨能力和适用性有所增强．

［1］ 王炳坤. 城市规划中的工程规划[M]. 天津：天津大学，2011.

［2］ 谷卓木. 农村电网规划方法的研究与实现[M]. 哈尔滨：东北农业大学，2009.

［3］ 李玉龙，孙元慧. 智能化新型城镇电网[J]. 农业电气化，2014(4)：12-16.

［4］ 牛晓东，曹树华，卢建昌，等. 电力负荷预测技术及其应用[M]. 北京：中国电力出版社，2009：11-15.

［5］ 肖 白，杨修宇，穆 刚，等. 基于元胞历史负荷数据的负荷密度指标法[J]. 电网技术，2014，38(4)：1,014-1,019.

［6］ 孙 威. 基于负荷密度指标的配电网空间负荷预测方法研究[D]. 重庆：重庆大学，2010.

［7］ 杨修宇. 基于负荷密度指标的空间负荷预测方法研究[D]. 吉林：东北电力大学，2014.

［8］ 朱前进. 模糊贴近度理论在空间负荷预测中的应用[J]. 广西电力，2009(3)：27-30.

［9］ GB50293—1999，城市电力规划规范[S].

The Power Load Forecasting of Modern Town Based on Load Density Method

XU Ya-ling，HUANG Min-de
(School of Control and Mechanical Engineering，Tianjin Chengjian University，Tianjin 300384，China)

Safe,stable and adequate power network is the foundation of modern towns’ development. However it is the first thing to forecast power load of power planning. Previous the load density index is usually obtained by simple analogy and experience which can hardly meet the accuracy requirements．This article,using the theory of fuzzy nearness,makes the load density index more scientific and accurate. By taking a modern town in Anhui Province as an example of power load forecasting,the authors calculate the load density index values. Example shows that the method is reasonable,clear,and practical.

power network；power load forecasting；load density index method；fuzzy nearness

TM715.1

A

2095-719X(2015)02-0139-05

2014-09-26；

2014-11-14

徐亚玲（1989—），女，安徽安庆人，天津城建大学硕士生．