方法检出限三个评估方法标准解读与比较

李玉武 任立军 王婧瑞 狄一安

（国家环境分析测试中心，100029北京）

方法检出限三个评估方法标准解读与比较

李玉武 任立军 王婧瑞 狄一安

（国家环境分析测试中心，100029北京）

文献中有多项方法检出限评估标准，如何正确理解和运用这些标准得到可比较的参数对基层实验室具有指导意义。对目前国内外方法检出限评估方法标准进行了系统总结和梳理，介绍了不同方法的特点、适用范围和注意事项。利用实验室实例和文献数据，比较了三种代表性方法计算结果。基于科学性和可操作性的原则，针对不同需求，提出了检出限评估改进建议及实施方案。

分析化学；方法检出限；评估方法标准

0 前言

检出限是分析方法基本性能参数之一，无论是开发新方法，制修订标准，以及实验室检测能力确认，常规检测报告附录，都会涉及方法检出限的实验设计和评估。这是评估实验室对于低浓度样品检测能力和质量保证的一个重要指标。对检出限的分类、方法探讨、结果比较一直是研究热点［1-13］。根据美国EPA［14］、国际组织IUPAC［15］、美国ASTM标准［16］以及ISO标准［17］制定的国内标准，如国家环境保护标准HJ 168-2010［18］，GB/T 17378.2-2007［19］，GB/T 27415-2013［20］为规范检出限评估奠定了良好基础。这些标准分别代表了不同方法原理，不同计算途径和不同的适用范围。这些方法的特点、使用条件、公式推导、结果合理性判断及相互之间计算结果的比较文献中很少报道。

本文对目前国内外方法检出限评估标准进行了系统梳理，介绍了不同方法的特点、适用范围和注意事项，利用实验室实测数据和文献数据，比较了同一套数据、不同评估方法的计算结果。基于科学性和可操作性的原则，针对不同需求，提出了改进检出限评估方法建议及实验方案。

1 实验部分

1.1 数据来源

方法检出限计算所采用的测量数据来自文献和笔者所在实验室。因篇幅有限未在本文列出，读者需要时可向本文作者索取。

1.2 计算方法

1.2.1 单浓度样品

此方法以美国EPA标准［14］为代表，国内环境保护标准HJ 168-2010［18］等效采用了此标准。按下列步骤准备一系列已知目标物浓度溶液或基体加标样品：

（1）根据分析方法标准、文献值、仪器说明书或仪器设备准确度估计方法检出限；

（2）准备第一批两份5倍检出限预估值溶液或加标样品；

（3）按照分析方法操作全程序（如需要样品消解，应包括消解步骤）准备样品，测量，记录结果；

（4）如果样品测定结果回收率在70%～130%，则转入以下步骤，否则重新估计检出限，增大样品加标浓度；

（5）配备5份或更多同样浓度样品。注意最好不要在同一天或同一批次完成所有样品制备。建议每天制备两份样品，这样可以得到更具代表性方法重复性数据；

（6）计算全部测量结果的平均值和标准偏差，按下列公式计算检出限：LD＝t（1-0.01，n-1）×s（其中LD为方法检出限；s为测量数据标准偏差；t为自由度为n-1，置信度为99%时的t分布（单侧）；

（7）得到检出限计算结果后，按下列核查点评估结果合理性：

① 加标量是否小于检出限计算值10倍？如果是，表示样品浓度或加标量满足要求；

②加标量是否大于检出限，且两者比值在2～5之间？如果是，表示样品浓度或加标量合适；

③检出限实验过程是否满足方法标准要求？

④信号与噪音比值（S/N）是否在适当范围（测量值平均值/测量值标准偏差≥5，或3～10）？

⑤各样品测量结果回收率平均值及范围是否合理（70%～130%）？

如果通过了所有这些核查点，则可以根据检出限判断实验室是否满足实际样品检测需求，否则应改进方法，或更换仪器。

（8）取另一份样品溶液（单目标化合物：2～3倍检出限，多组分目标化合物：1～4倍）进行检测，是否能够检测出。

（9）对于多点加标测量数据，如果各浓度点测量值标准偏差无显著性差别，可将各标准偏差进行合并处理［18］。

1.2.2 工作曲线法

此方法以ISO标准［18］为代表，国内标准GB/T 17378.2—2007［19］附录和文献［11-12］均有介绍。主要步骤如下：

（1）根据分析方法标准、文献值、仪器说明书或仪器设备准确度估计方法检出限；根据方法检出限预估值设计工作曲线浓度范围（如0，1/4，1/2，1，2，4，8倍检出限预估值），最大值建议不超过预估值10倍；工作曲线各点应涉及样品制备各环节；

（2）根据浓度设计方案，取不同浓度水平（I≥5），每个浓度水平重复制备J个样品（J≥3），建议每个样品重复测量2次，取平均值；

（3）根据统计学原理，判断实验数据中是否存在离群值；根据浓度与相同浓度样品测量重复性数据（标准偏差）之间的函数关系判断工作曲线类型：同方差或异方差。函数关系为常数者为同方差，标准偏差随浓度增加而明显增加者为异方差；

（4）同方差模型：数据采用经典最小二乘法（OLS）计算工作曲线斜率（b），截距，得到残差均方根（sy）。按公式（1）计算方法检出限（假定实际样品重复制备1次，t和δ可查表求得［17］）：

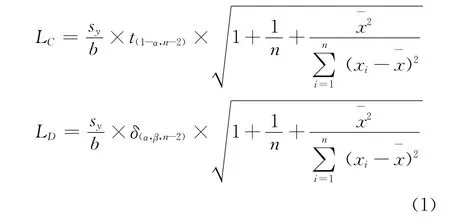
当α＝β，I≥5时，LD＝2×LC。

式（1）中LD为检出限，Lc为空白溶液临界限；sy为测量数据yi与回归拟合公式计算值差值均方根：sy＝，n为参与测量的样品个数，xi某样品浓度值；b为工作曲线斜率；t和δ分别为t分布和分位数值。

（5）异方差模型：数据采用权重最小二乘法（WLS）计算工作曲线斜率，截距，得到残差均方根。文献［17］采用迭代法计算权重因子。采用文献［21］提供的MDL＿Estimator?软件可以得到相近结果。

1.2.3 数学模型法

数学模型法以美国ASTM标准［16］为代表。国内标准GB/T 27415-2013［20］等效采用了ASTM标准。此标准中，方法检出限有下列新定义：

实验室间检出限LD：能以较高概率检出的最小浓度，即在90%置信水平下，浓度是LD的样品被检出的实验室比例为95%，浓度是0的样品不被检出的实验室比例是99%。

实验室间临界值LC：在90%置信水平下，浓度为0的样品正确不被检出的实验室的比例是99%。

实验方案主要步骤如下：

选择痕量或接近痕量浓度的分析物。校准模型R应涵盖0到工作曲线最大浓度范围内的样品。工作曲线点至少选择5个，例如：0，LD/4，LD/2，LD，2×LD，4×LD。

作浓度关于标准偏差s的散点图，并使用最小二乘法（OLS），对s与浓度c进行线性回归，如果是常数模型，LD＝（k1＋k2）×s，其中k1，k2为单侧区间统计容忍系数，可查表求得［23］。

如果是线性模型，浓度与标准偏差关系式如下：s＝g＋h×c（回归系数为g和h，其它还有指数模型s＝g×eh×c等可供选择）。校准模型R拟合采用加权最小二乘法（WLS）：

y＝a＋b×c（回归系数为a和b）；权重因子w＝1/s2。

使用直线或指数模型时，可分别按式（2），（3）进行迭代计算：将每次迭代所估计的LD代入到递归式中，给出新的LD，直至迭代求得连续LD之差小于1%。

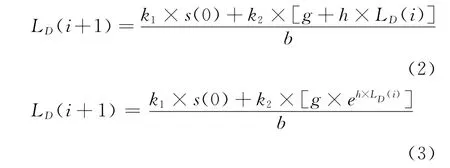
其中初始值按式LD（i＝0）＝2×LC；LC＝k1×s（0）/b计算，其中s（0）＝g，斜率b是加权最小二乘法计算结果。

2 结果与讨论

根据方法检出限实验方案选取浓度水平的多少，可将文献中方法检出限评估标准分为两大类：以美国EPA（1997）标准和IUPAC（1998）为代表的单浓度水平重复实验数据评估方法和以ISO 11843.2-2000和美国ASTM D6091-2007为代表的多浓度水平工作曲线法。各种处理途径之间关系见图1。

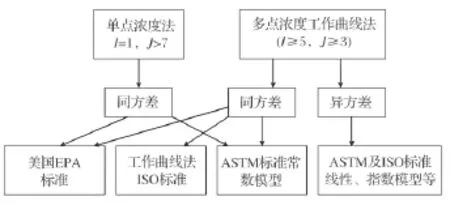
图1 方法检出限常见评估标准方案示意图Figure 1 Schematic diagram of the evaluation standards of MDL.

2.1 美国EPA标准：单浓度重复实验方法

目前文献中或检测报告中大多采用根据单浓度重复实验结果评估得到的“检出限”，实际上是空白溶液的测试上限（LC），即与空白溶液有明显差别的值（临界值）。如果按此浓度配制样品溶液，测试方法能检出目标物的几率仅为50%。容易犯“假阳性”错误（Ⅱ类错误）［10］。在美国EPA标准条款中，建议在得到“检出限”结果后应该按2倍的LC检查响应值。有明显信号检出，检出限评估工作才算告一段落。实际工作中，这一步骤经常被忽略。这里的2倍的LC，有时也称为“保证限”［2223］，这相当于其它计算检出限方法标准［16，20］中定义的检出限LD。

此方法标准有一个重要前提，即假定实验数据是同方差模型。如果在加标浓度范围内，测量数据标准偏差与浓度函数关系不是常数（或不同浓度测量数据标准偏差存在显著性差异），可考虑用工作曲线法中的异方差模型处理数据，但首选降低浓度进行下一轮实验。此方法标准原则上仅适合实验室内部方法检出限评估，未涉及实验室间方法检出限测量数据的处理。

2.2 ISO标准：工作曲线法

2.2.1 同方差模型

工作曲线法有两种应用类型，取决于浓度标称值（x）与仪器响应值（或浓度测量值）y标准偏差数据关系是“同方差”还是“异方差”。同方差是指y测量数据标准偏差与浓度大小基本无关，如相关则是异方差。GB/T 17378.2-2007附录涉及的是工作曲线法（同方差）计算公式，ISO 11843.2-2000同时提供了同方差和异方差两种条件下的计算公式。原则上，整套实验数据中应包括同一浓度水平的重复性配制样品测试数据才能运用工作曲线法，如MDL＿Estimator?免费计算软件对此有明确要求。如果没有重复性数据，也可根据公式（2）进行计算，其依据基于以下考虑：工作曲线回归分析得到的方差可分解为线性模型可解释的方差及实验数据重复性方差。大多数情况下，分析方法的线性关系已经得到确认，此时回归分析结果残差均方根代表了不同浓度点的平均重复性标准偏差。因此，即使每一个浓度只测量了一次，同样可以根据工作曲线法得到一段低浓度范围测量值平均标准偏差，进而根据相关公式计算检出限。但其应用范围仅限于同方差模型。由此计算得到的检出限可以作为3.1节方法检出限预估值。值得指出的是，其结果可靠性肯定不及有重复性测试数据得到的计算结果。

GB/T17378.2-2007和ISO11843.3-2000中的计算公式大同小异，都涉及LC和LD计算。ISO标准中规定两种风险率均为0.05，且推出简化计算式：LD＝2×LC。这个系列标准强调的是α＝β＝0.05的置信区间（非容忍区间），也就是说仅强调了对α的控制，并不注重于β的控制。

将文献［17，19］中计算公式进行简化得到（4）式，在ExcelR○软件平台上采用迭代法编写模板进行计算。

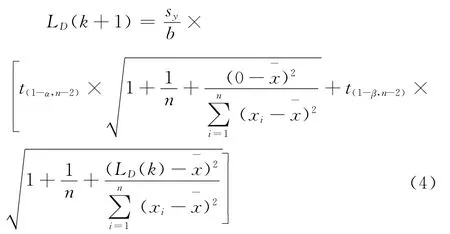
其中b为工作曲线斜率，sy为回归分析残差均方根。上述公式推导如下。

根据线性回归分析相关计算公式，在空白溶液和检出限附近，浓度为0和LD（检出限）测量值标准偏差分别为（参见图2）：

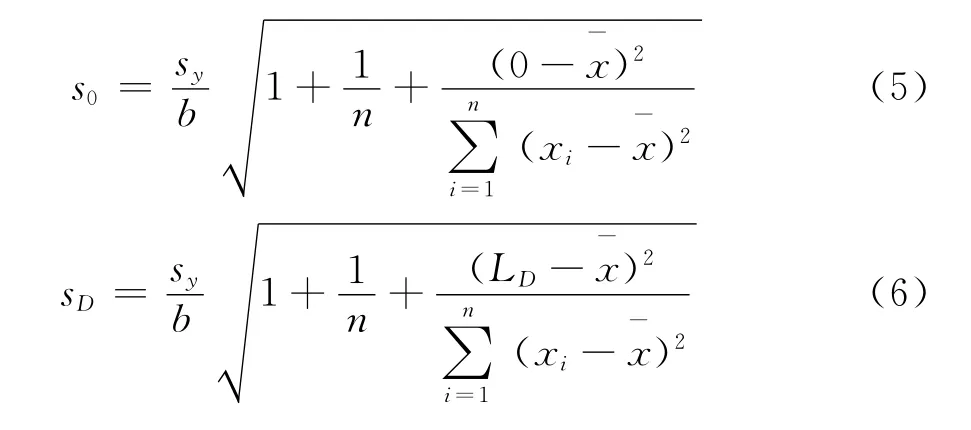
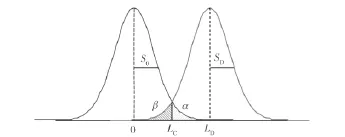
图2 工作曲线法检出限迭代计算公式推导示意图Figure 2 Schematic diagrams for iterative calculation formula derivation of MDL by linear calibration model.

根据统计学基本原理有：

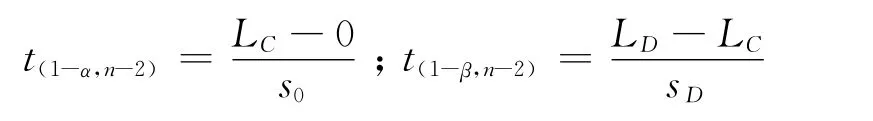
由上式可以分别得出，LC＝t（1-α，n-2）×s0；LC＝LD-t（1-β，n-2）×sD

将两式重新整理可得：LD＝t（1-α，n-2）×s0＋t（1-β，n-2）×sD

将公式（5），（6）代入，则有：

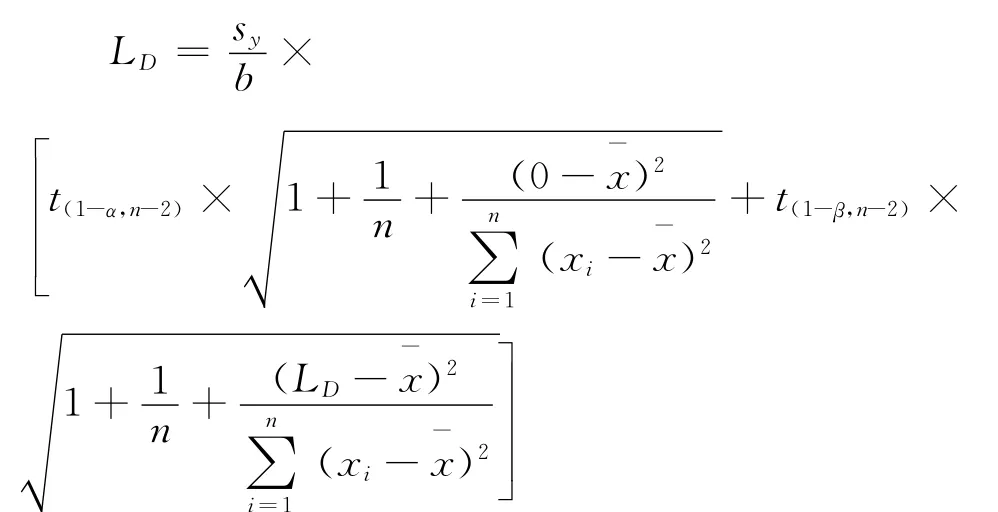
从上述公式中可以看出，等式左、右两侧同时含未知量LD。这时可以采用迭代法处理。其计算途径是先计算LD初始参数LD（k＝0）＝2×LC，代入计算公式右侧，得到LD（k＝1）计算结果，然后再代入计算公式右侧，得到LD（k＝2）计算结果，如此反复，迭代数轮后直到前后两次结果在第三位有效数字上无区别。这种计算公式推导与原标准［17，19］相比，思路清晰，易于理解，算法很容易在常见办公软件平台上实现。

与ISO 11843.2不同，此计算公式可根据实际需要设定t（1-α，n-2）和t（1-β，n-2），假阴性和假阳性两种风险率可以自由设定。t临界值（单尾，对应于α＝0.01，β＝0.05）可以在ExcelR○软件平台上利用计算函数tinv（2×0.01，n-2）和tinv（2×0.05，n-2）得到。应用公式（1）或公式（4）时，应注意下列几点：

（1）与日常检测分析未知样品的校准计算用工作曲线不同，用于计算检出限的工作曲线浓度范围应控制在预计检出限LD的1/2到10倍。工作曲线范围内，不同浓度的测量值标准偏差是常数。在低浓度区域，大多数情况下容易满足此公式同方差计算条件。根据每个浓度水平重复配制样品的测量数据，很容易判别是否满足同方差条件。但如果每个浓度水平仅有一个样品的测量值，可以尝试采用下列方式进行判断［25］：回归分析结果与实验值残差绝对值｜ei｜与样品浓度水平无关，则为同方差。如果显著相关，则为异方差。如果是异方差数据采用同方差模型计算，其方法检出限结果会明显偏高。

（2）工作曲线的数据点n，应等于浓度水平点设计个数（I）乘以每个浓度点样品重复配制个数（J）。与每个样品溶液在仪器上重复测量次数（L）无关。如果重复性配制样品测试数据分散在数周或数月内完成，其代表性更好。这与top-down方法评估测量不确定度涉及的期间精密度概念相同［26-27］。原则上工作曲线法对应于每个浓度水平均应有重复配制样品。如果没有重复样品，计算公式也能给出结果，但其可靠性降低。好结果需要投入相应的工作量。

（3）α，β设定值不同，LC和LD计算结果也不同。根据统计容忍区间的概念，也可以得到下列条件下的计算结果：在90%置信水平下，浓度是LD的样品被检出的实验室的比例为95%，浓度是0的样品不被检出的实验室的比例是99%。此时公式（1）中t（1-α，n-2）和t（1-β，n-2）将由k1和k2取代。k1和k2值可以从文献［27］查得。但此时如直接采用ASTM标准数学模型法的常数模型，计算过程将更为简单。常数模型时，（k1＋k2）/k1＝1.72，约等于2，可用作简便处理：LD＝LC×2，与ISO11843.2简化计算式相同。推导如下：根据ASTM标准中常数模型计算公式，LD＝（k1＋k2）×s，根据美国EPA标准有计算公式；LC＝t1×s，根据同方差假设，两式相除，LD/LC＝（k1＋k2）/t1，因为k1＞t1，因此有（k1＋k2）/t1＞1.72。模拟计算结果表明，（k1＋k2）/t1数值范围为2.0～2.2，故有LD≈LC×2。

2.2.2 异方差模型

当浓度与标准偏差关系不是常数模型时，应用公式（1）或公式（4）时计算结果会明显偏高。异方差工作曲线法计算途径主要思路是利用不同浓度水平实验数据标准偏差，取其平方的倒数设定为不同浓度点权重因子的初始值。采用迭代法不断更新此权重因子。得到权重因子后对浓度与响应值进行权重最小二乘法（WLS）得到工作曲线斜率。然后根据相关公式［17］计算检出限。由于低浓度点标准偏差小，因而权重因子大，这就意味着在进行浓度与响应值、浓度与标准偏差的函数关系回归分析时，检出限附近低浓度点将发挥更大作用。

ASTM标准数学模型法同样根据浓度与标准偏差关系拟合表达式，取不同浓度下标准偏差计算值作为权重因子，但计算权重因子时不涉及迭代计算。对于某些特殊情况，其拟合精度可能不及ISO标准法。但ASTM模型法还可以选用指数或二次函数等模型描述浓度与标准偏差关系，而不仅仅是线性模型。ISO标准法仅限定于线性函数模型。如果线性模型不合适时（如有时线性模型外推到浓度为0时，超出实验范围），异方差模型计算结果会偏低。

2.2.3 应用MDL＿Estimator?免费软件计算检出限

MDL＿Estimator?免费软件［22］采用了ISO 11843.2标准方法原理，对同一套数据可方便、快速提供依据同方差（OLS）和异方差（WLS）两种算法得到的检出限计算结果。但软件要求同时提供有样品配制重复性要求的不同浓度水平数据。如果同一浓度水平样品没有重复测量数据，软件无法计算。根据软件编制者建议，当OLS和WLS提供的结果相差不大时，可判定为同方差类型，此时建议采用OLS算法计算结果。两者相差较大时，可判定为异方差类型，建议采用WLS计算结果。实验数据结果表明，两者有明显区别时，首先考虑缩小工作曲线浓度范围（但仍需保留5个浓度水平），观察两者差别是否已经减小。可以结合对数据sd（c）函数关系（常数、线性等）及两种结果（OLS和WLS）比值小于2来进行判断、验证。原则上，如果不是常数模型，则应更多关注低浓度点数据，即采用WLS计算结果。但最终结果需要根据多条途径对合理性进行判断，并根据检出限计算值配制样品加标溶液进行验证。

多套数据验证结果表明（参见表1），MDL＿Estimator?免费软件同方差数据计算结果与ISO标准算法两种风险率控制率均为0.05，计算结果基本相同。由此推断，软件计算结果基本上采用了ISO标准算法，缺点是相关参数（如α、β）仍无法根据实验室需要进行调整。这个算法同样强调的是α＝β＝0.05的置信区间（非容忍区间），也就是说仅强调了α的控制，并不注重于β的控制。

2.3 ASTM标准：数学模型法

与ISO标准工作曲线法利用预测区间标准偏差计算式评估检出限不同，ASTM标准提出的s（c）数学模型法直接利用浓度与标准偏差函数关系拟合、权重最小二乘法及检出限定义得到迭代计算式。其结果准确性直接与浓度与标准偏差函数关系拟合精度相关。根据其实验方案设计要求，工作曲线浓度范围应控制在（1/4～4）倍预估检出限浓度内。准确建立此浓度范围内的重复性标准偏差函数关系是采用此方法评估检出限的关键环节。其拟合精度可以根据残差均方根和R2来判断。

此标准有下列主要特点：

（1）概念定义遵循了Currie原则［1］，并规范了检出限术语定义；

（2）建立标准偏差随水平浓度显著变化的数学模型，采用多点实验数据进行拟合。常数模型仅是其中一个特例。此方法重点是处理异方差实验数据；

（3）给出基于实验点n的90%置信下单侧容忍区间，重点强调要同时考虑α和β的水平控制。

（4）计算方法基于不同实验室间检出限实验数据，由此得到的方法检出限与低浓度样品实验室间再现性标准偏差有关。

根据ASTM标准关于方法检出限实验方案顶层设计要求，需收集（7～10个）不同实验室对统一实验方案开展的协同测试数据，然后再进行下一步数据处理。此方法需要来自多家实验室的原始测量数据，实验进度不易控制，成本大，要求不容易满足。此方法原则上可推广应用于实验室内部方法检出限评估。即使全部工作集中在一个实验室完成，实验进度有保证。但实验工作量也明显大于经典的基于单浓度重复实验的美国EPA标准方法。工作曲线法（同方差，I≥5，J＝1）工作量与单浓度法相当，但结果可信度显然不及多点、多次重复配制样品（J≥3）、更全面的实验方案。

ASTM数学模型法有扎实的数理统计基础，浓度与标准偏差之间存在明显的函数关系且这种函数关系拟合质量高是取得可靠结果的重要前提。选用不同数学函数表达式时，应首先对浓度与标准偏差数据作图，观察数据分布情况。选择不同函数表达式应优先照顾低浓度点。结果的可靠性与采用的统计分析方法、实验数据数量和质量直接相关，三者圆满结合才可达到实验目的。

与ISO标准一样，异方差计算公式比较繁杂，ASTM标准计算过程需要有经验的人指导，不便于基层实验室使用。将ISO标准异方差模型条件下计算公式和ASTM标准计算编写成可在Excel通用办公软件上使用的小程序，将是推广普及这二项标准的有效途径。

2.4 检出限不同评估方法结果比较

为保证计算结果的准确性和一致性，首先采用ISO标准和ASTM标准附录示例数据，通过与示例计算结果对本文编写的计算公式及程序进行了验证。同方差模型数据：原ISO标准附录结果为LC＝0.086，LD＝0.17，本文计算结果分别为0.086和0.17。异方差模型数据：原ASTM D6091标准附录计算结果为LC＝0.511，LD＝1.32（mg/L），本文计算结果分别为0.508和1.32；原ISO标准附录计算结果：LC＝5.63，LD＝16.0（pg/100mL），本文计算结果分别为5.63和16.0。验证结果表明，本文计算结果与原标准示例结果完全一致，计算公式和程序通过检验。

根据从标准附录和文献中收集的检出限实验数据，用三项检出限评估标准方法计算同一套数据（分为同方差和异方差两种类型），结果分别见表1，表2。为便于核对，表1和表2还列出了原始数据来源及相关计算参数，如α，β，t值或分位数。

表1汇集的计算结果表明：

（1）同一计算方法，α风险率取值不同（α＝0.01或0.05）直接得到不同的t值，其结果有差别。α＝0.01对应的结果大于α＝0.05计算所得结果。ASTM标准采用统计容忍区间系数k1和k2，其值也明显大于置信区间系数t1和t2。

（2）取全部测量数据或仅取相同浓度水平数据的平均值参与计算，对结果有影响。这主要反映在t值的取值对结果的影响和参加回归分析数据个数对残差均方根的影响。数据个数多，t值小。与全部数据参与计算相比，取平均值参与计算，回归分析结果残差均方根小。根据ISO标准的要求，推荐全部测量数据参与计算。

（3）MDL＿Estimator?软件与ISO标准计算结果基本吻合。这表明，此软件采用的算法和α取值与ISO标准完全相同（α＝0.05）。

（4）ASTM标准与ISO标准两种方法计算结果基本吻合。用美国EPA标准求得临界值LC后，再乘以2，得到的检出限与多点工作曲线法（ISO标准）和ASTM标准计算结果基本一致。但单点实验方案的工作量会明显减少。

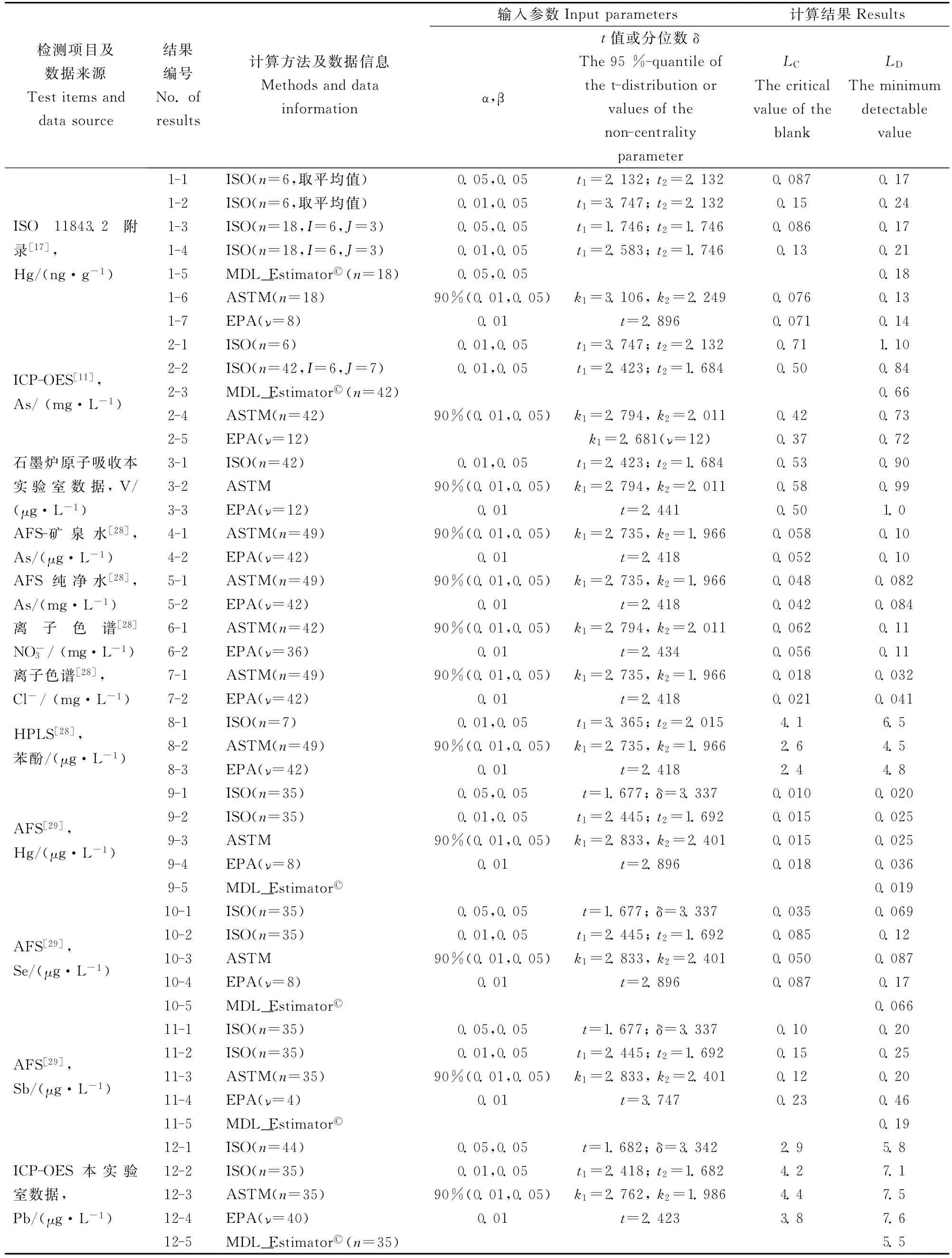
表1 同方差模型检出限不同计算方法结果比较Table 1 Comparison results of MDL by different evaluation standards using homoscedasticity variance model

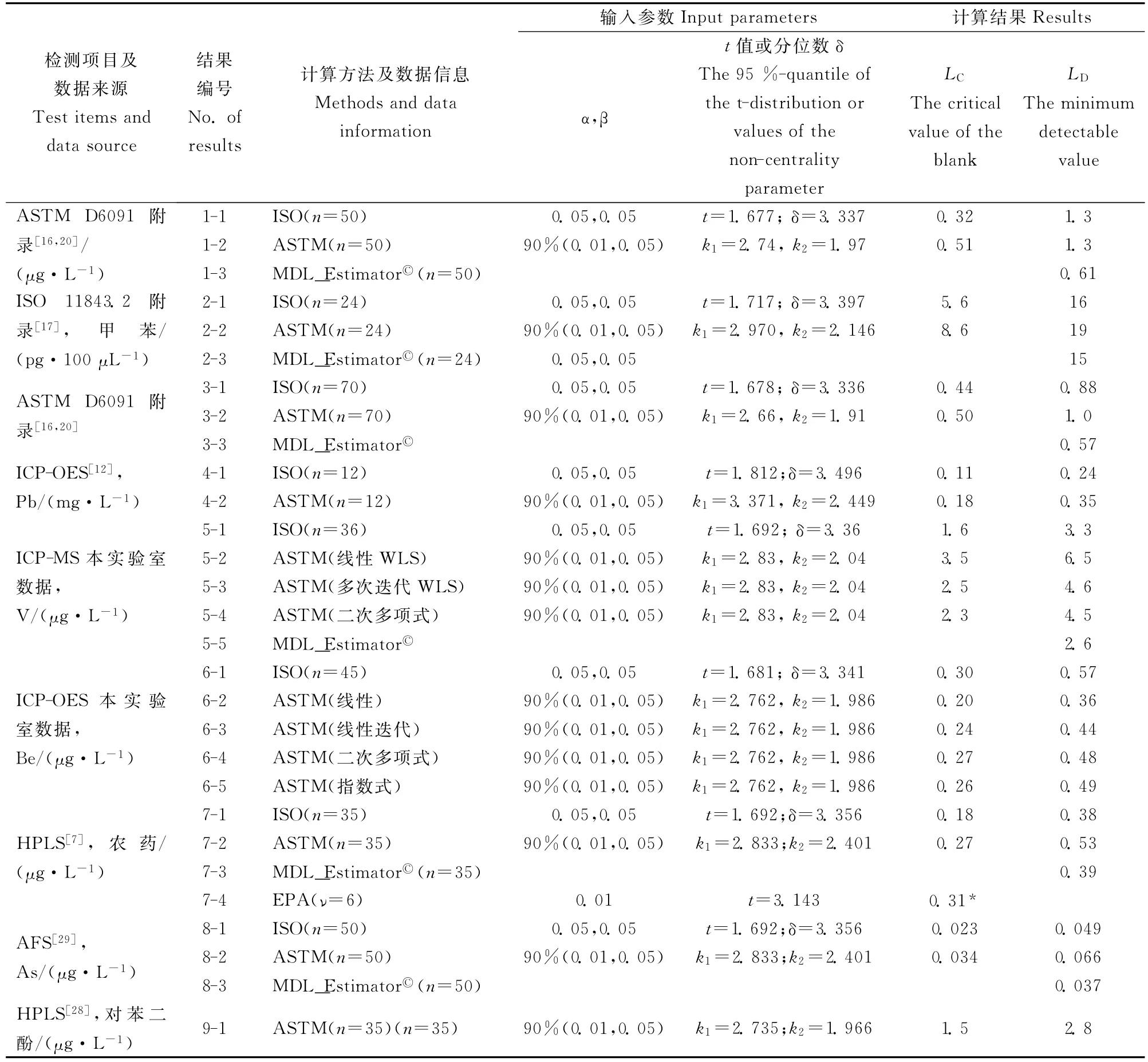
表2 异方差模型检出限不同计算方法结果比较Table 2 Comparison results of MDL by different evaluation standards by heteroscedasticity variance model

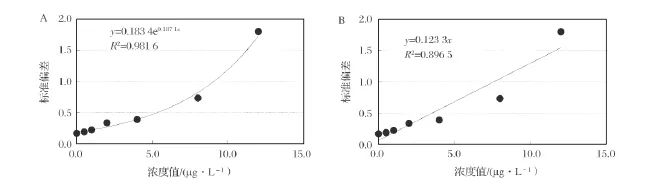
图3 ASTM标准中模型选择对结果的影响（A：指数模型；B：线性模型）Figure 3 Effect of models in ASTM standard on MDL result（A：Eexponential model；B：Linear model）.

表2列举了异方差数据计算结果。从表2数据可以看出，ISO标准和ASTM标准采用的方法基于不同计算原理，但结果基本相同。采用ASTM标准方法时，拟合模型为多次迭代WLS和二次多项式对结果无明显影响。但对于某些数据 （参见图3和表2第6套数据）线性模型与指数模型结果有所差别。线性模型外推到浓度为0时，与实验值明显不符。选择模型时应优先照顾低浓度点。使用MDL＿Estimator?软件得到的结果与ISO标准计算结果基本相同，有可比性。

3 结论

目前文献中常见的根据美国EPA标准单浓度样品重复实验结果评估得到的“检出限”，大多是空白溶液的测试上限（LC），即能与空白溶液有明显差别的值。如果按此浓度配制样品溶液，测试方法能正确检出的几率仅为50%。方法检出限结果偏低。以ISO和ASTM标准为代表的工作曲线法和数学模型法充分考虑了低浓度区间目标物浓度与测量值标准偏差之间函数关系，其计算公式有坚实的数理统计基础。在人力、物力有保证的条件下，是评估方法检出限的首选方案。缩小浓度区间可有效避免异方差情形的出现。浓度与标准偏差之间是否存在明显的函数关系且能得到高质量函数关系拟合表达式是异方差情形下取得可靠结果的重要前提。综合考虑三项标准计算方法的特点及可操作性，推荐考虑下列实验方案：首先通过低浓度范围工作曲线（I＝5，J＝1）估计方法检出限，在此基础上以5倍左右预估值设计单浓度实验方案。根据实验数据计算临界值LC。然后与ASTM标准常数模型的处理方案相结合，LD＝2×LC。核对并判断方法检出限计算结果的合理性。这是在有限的实验工作量情况下，有望达到事半功倍效果的一条途径，值得尝试。

［1］Currie L A.Detection：International update，and some emerging di-lemmas involving calibration，the blank，and multiple detection decisions［J］.Chemometrics and intelligent laboratory systems，1997，37（2）：151-181.

［2］Thomsen V，Schatzlein D，Mercuro D.Limits of detection in Spectroscopy［J］.Spectroscopy，2003，18（12）：112-114.

［3］Ernesto Bernal.Limit of Detection and Limit of Quantification Determination in Gas Chromatography［EB/OL］.（2014-2-26）［2014-8-15］.http：//dx.doi.org/10.5772/57341.

［4］Voigtman E.Limits of detection and decision：part 1［J］.Spectrochimica Acta：Part B，2008，63（2）：115-128.

［5］Corley J.Best practices in establishing detection and quantification limits for pesticide residues in foods［M］//Phillip W.Lee，Hiroyasu Aizawa，Aldos C.Barefoot，John J.Murphy.Handbook of Residue Analytical Methods for Agrochemicals.John Wiley ＆Sons Ltd，2003：1-18（http：//files.instrument.com.cn/Files-Center/20100911/2010911131837145539.pdf）.

［6］冉敬，杜谷，杨乐山，等.关于检出限的定义及分类的探讨［J］.岩矿测试（RockandMineralAnalysis），2008，27（2）：155-157.

［7］丁怡，彭程.多种方法评估液相色谱方法检出限的初步探讨［J］.现代食品科技（ModernFoodScienceand Technology），2009，25（11）：1372-1373，1314.

［8］蔡潞莎，胡奇，芮三亚.蔬菜中有机磷农药多残留分析：方法检出限的对比研究［J］.食品科学（FoodScience），2006，27（11）：449-454.

［9］鲁静，付凌燕，王旭.质量分析方法验证中检出限和定量限测定方法探讨［J］.中国药品标准（DrugStandards ofChina），2012，13（1）：33-35.

［10］Calfstone.带您了解检出限［EB/OL］.（2008-8-15）［2014-8-15］.http：//wenku.baidu.com/view/dd231524aaea998fcd220e00.html.

［11］Kircher Carl C.，Detection and Quantitation or How to Make Something out of Nothing［EB/OL］.（2013-11-25）［2014-8-15］.http：//wenku.baidu.com/view/c8c713b1e53a580217fcfe0e.html.

［12］Calculations of MDL by Hubaux and Vos Method［EB/OL］.（2004）［2014-8-15］.http：//www.chemiasoft.com/chemd/node/59.

［13］Hubaux A，Vos G..Decision and Detection Limits for Linear Calibration Curves［J］.Analytical Chemistry，1970，42（8）：849-855.

［14］U S environmental protection agency.Guidelines establishing test procedures for the analysis of pollutants［S］.（appendix B，part 136，definition and procedures for the determination of method detection limit），1997：265-267.

［15］The International Union of Pure and Applied Chemistry（IUPAC）.IUPAC compendium of Analytical Nomenelature［S］.1998.

［16］ASTM Committee Dl9on Water and ASTM of Subcommittee D19.02on General Specifications，Technical Resources，and Statistical Methods.ASTM D6091-2007，Standard Practice for 99%/95%Inter-laboratory Detection Estimate（IDE）for Analytical Methods with Negligible Calibration Error［S］.

［17］Technical Committee ISO/TC 69，Applications of statistical methods，Subcommittee SC 6，Measurement methods and results.ISO 11843.2—2000，Capability of detection-Part 2：Methodology in the linear calibration case［S］.

［18］环保部科技司标准处.HJ 168-2010环境监测分析方法标准制修订技术导则［S］.北京：中国环境科学出版社，2010.

［19］全国海洋标准化技术委员会.GB 17378.2-2007海洋监测规范 第2部分：数据处理与分析质量控制［S］.北京：中国标准出版社，2007.

［20］全国认证认可标准化技术委员会.GB 27415-2013分析方法检出限和定量限评估［S］.北京：中国标准出版社，2013.

［21］SEMI International，Guide for Determination of Method Detection Limits，SEMI International Standards 1998：Book of SEMI Standards，Process Chemicals（or Gases）Volume（1998）［EB/OL］.（2010-10-10）［2014-8-15］.http：//bbs.instrument.com.cn/shtml/20101010/2850614/.

［22］理学电机工业株式会社应用研究中心、中国理学XRF光谱仪用户协会.X-射线荧光分析原理与应用［M］.北京，1997：75.

［23］陆晓华.化学计量学［M］.武汉：华工理工大学出版社，1997.

［24］刘振亚.计量经济学教程［M］.北京：中国人民大学出版社，1997：190.

［25］狄一安，孙海容，孙培琴，等.用质控图和稳健统计-迭代法评估环境检测实验室测量不确定度［J］.岩矿测试（RockandMineralAnalysis），2014，33（1）：57-66.

［26］周瑞，狄一安，于跃，等.用质控图法和稳健统计法评估热裂解-原子吸收光谱法测量固体样品汞含量的不确定度［J］.中国无机分析化学（ChineseJournalof InorganicAnalyticalChemistry），2015，5（2）：1-8.

［27］全国统计方法应用标准化技术委员会.GB/T 3359-2009数据的统计处理和解释-统计容忍区间的确定［S］.北京：中国标准出版社，2009.

［28］李君霞.分析检出限的实验测量和计算方法的研究［D］.北京：北京化工大学，2012.

［29］环保部科技司标准处.HJ/T 674-2014水质-Hg、As、Se、Bi、Sb的测定-原子荧光法［S］.北京：中国环境科学出版社，2014

Interpretation and Comparison of Three Evaluation Methods of Method Detection Limit

LI Yuwu，REN Lijun，WANG Jingrui，DI Yian
（NationalResearchCenterforEnvironmentalAnalysisandMeasurements，Beijing100029，China）

Several evaluation standards of method detection limit（MDL）have been reported in literatures.It is important to understand and use correctly these standards so that it could obtain reliable parameters for guiding base laboratories.In this paper，the evaluation standards of MDL at home and aboard were systemic analyzed and summarized，and their features，application scope and key points were introduced.Comparison results of three typical evaluation standards were presented using real data sets from literatures and the author’s laboratory.The modified procedure for the evaluation of MDL was proposed for different laboratory requirements according to scientific and maneuverability principles.

analytical chemistry；method detection limit；evaluation standard

O651

A

2095-1035（2015）03-0024-10

2015-04-22

2015-05-24

国家重大科学仪器设备开发专项（2011YQ140147；2011YQ170065；2014YQ060773）资助

李玉武，男，研究员，主要从事分析化学数据处理研究。E-mail：liyuwu＠cneac.com

10.3969/j.issn.2095-1035.2015.03.007