认识与超越：小学数学教学的应然取向

江苏扬州市广陵区教育局（225000） 汤雪峰

当前，小学数学课程以学生数学“四基”的获得，“四能”的发展，以及对数学的情感、态度的培养作为重要目标。换言之，就是让学生通过有限知识的学习，掌握探索无限世界之本领。这就需要教师站在更高的视角去审视小学数学教学，实现从一般认识到理性超越。本文主要从文本之中与文本之外相结合的视角，以“审视课标、审视教材、尊重知识、尊重儿童”作为研究重点，探索小学数学教学实践的应然取向。

缘由

课标、教材、知识和儿童，是除教师之外最重要的教学要素。作为对小学数学教学的认识和超越，我们既要理解作为文本的课标和教材，更要读懂文本之外的数学教学知识和教育教学对象——儿童，真正做到审视课标、审视教材、尊重知识、尊重儿童。

课标和教材不是一成不变，而是经常变化的，所以我们一方面要认识作为文本的课标和教材，另一方面要超越文本，关注课标和教材的历史发展走向，及其背后的教育思想、教育原理、教育方法的演变，把握其实质，辨别其合理性，以改进我们的教育教学。

一百多年以来，小学数学课标和教材的多变性、不确定性，制约了其可靠性，所以我们在理解课标和教材的同时，要学会以科学的数学观、哲学观、教育观和历史观去审视之，实现认识上的超越。同时值得注意的是，现代数学基础确立以后，小学数学基础知识是相对稳定的，在小学数学教学研究和实践中，要给予足够的重视和尊重。此外，教育教学对象是活生生的儿童，我们要充分研究儿童，尊重儿童的年龄特征、个体差异，以及认知基础和认知经验的发展水平。

审视课标

课程标准是具有法规性质的课程改革纲领性文件，从1902年8月15日我国第一部由政府颁布，兼有小学数学课程标准功能的《钦定学堂章程》问世算起，一百多年间，我国小学数学课程标准前后发生了很大的变化。每一次变化都值得认真研究和对待。

比如，《全日制义务教育数学课程标准（实验稿）》倡导：在教学内容上，“学生的数学学习内容应当是现实的、有意义的、富有挑战性的，这些内容要有利于学生主动地进行观察、实验、猜测、验证、推理与交流等数学活动。内容的呈现应采用不同的表达方式，以满足多样化的学习需求。”在学习方式上，“有效的数学学习活动不能单纯地依赖模仿与记忆，动手实践、自主探索与合作交流是学生学习数学的重要方式。”在教学方式上，“教师应激发学生的学习积极性，向学生提供充分从事数学活动的机会，帮助他们在自主探索和合作交流的过程中真正理解和掌握基本的数学知识与技能、数学思想和方法，获得广泛的数学活动经验。”在教学活动中的师生关系上，“学生是数学学习的主人，教师是数学学习的组织者、引导者与合作者”。

然而，《义务教育数学课程标准（2011年版）》认为：“课程内容要反映社会的需要、数学的特点，要符合学生的认知规律。它不仅包括数学的结果，也包括数学结果的形成过程和蕴涵的数学思想方法。”“教学活动是师生积极参与、交往互动、共同发展的过程。有效的教学活动是学生学与教师教的统一，学生是学习的主体，教师是学习的组织者、引导者与合作者。”“学习应当是一个生动活泼的、主动的和富有个性的过程。认真听讲、积极思考、动手实践、自主探索、合作交流等都是学习数学的重要方式。学生应当有足够的时间和空间经历观察、实验、猜测、计算、推理、验证等活动过程。”

通过比较，不难发现：课标所倡导的，无论是课程内容、教学方式以及师生关系，十年前后变化就很大。可见，课标不是绝对真理，而且也很不稳定。

此外，二十一世纪以来我国义务教育数学课程改革在课程理念、课程目标、教材编制以及教学方式等几个方面和美国的很多做法极其相似。例如，在课程理念上，课程标准（实验稿）强调数学课程要实现“人人学有价值的数学；人人都能获得必需的数学；不同的人在数学上有不同的发展”，而美国1989年数学课程标准（NCTM）中提出“每个人都要学数学，他们学人人都需要的数学的机会是均等的”。在课程目标体系上，参照美国1989年数学课程标准，我国小学数学课程目标原来的“算术学科核心型结构”调整为美国特色的“条目并列型”结构。但是，中美两国的教育基础、教学传统以及社会价值等方面都存在很大的差异，因而我们在学习和理解课程标准时，一定不能盲从，要坚持积极而又审慎的态度，很有必要梳理一百多年来的小学数学课程标准的嬗变与坚守，遵循数学知识的本质、儿童的本性和教育的本义，探索出课程改革发展的应然走向，为儿童的数学学习扎实思想根基。

审视教材

有人认为“课本、课本，教学的根本”，这话有一定道理，但也未必全对。2001年，教育部颁布了《中小学教材编写审定管理暂行办法（试行）》，鼓励和支持有条件的单位、团体和个人参与中小学教材的编写工作。目前，全国已有10多种小学数学教科书在教学一线使用，出现了多种版本教科书竞相发展的局面。

现行小学数学教科书在编写结构上基本采用“大螺旋式”编排，即在六个年级教学内容的整体编排上采用螺旋式，而在每个单元上采用直线式。这样强调了数学内容内部每一领域的连续性与系统性。利用这种“小步子”“高密度”的方式编排单元知识，时间跨度大，学生容易遗忘，而且不能很好体现知识整体结构的系统性。这应该引起我们一线教师的重视。

另一方面，数学知识和数学思想是数学教科书编排的两条主线。数学知识是一条明线，它被明明白白地写在教材里，而数学思想则是一条暗线，需要教师挖掘、提炼，并在教学中凸显。数学思想相比数学知识，具有更高的概括性和包容性，所以数学思想对学生的数学学习品质，以及学生的成长和发展具有更重要的影响，它应成为数学教育的重要内容。

例如，苏教版小学数学教科书一年级下册（2012年版）第1页“20以内的退位减法”（如图）。

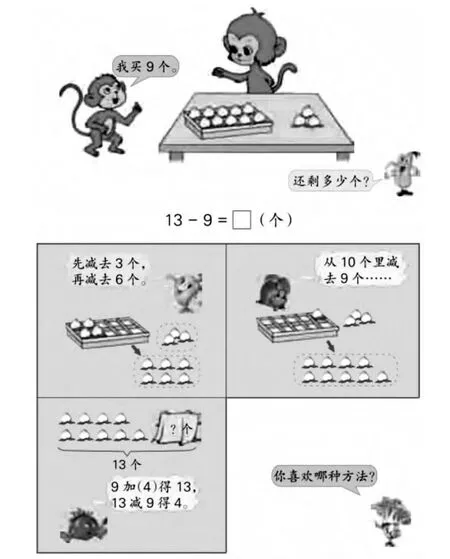
这里应该利用好几种算法，比如第3种算法“算减想加”。我们都知道要引导学生思考：要算13－9＝？想9＋？＝13。因为 9＋4＝13，所以 13－9＝4。这样的过程就是根据“减法的意义”进行演绎推理。这样，也就适时进行了推理思想的教学。

尊重知识

先弄清数学知识的来龙去脉、纵横联系，以及背后的精神、思想和方法，再根据本班学生的情况进行教学设计和实施，这应该是小学数学教学的上乘境界。

学生学习数学的过程实际上是一个数学认知的过程，在这个过程中学生在教师的引导下，把数学知识结构转化成自己的数学认知结构。教师只有充分把握数学知识自身的结构（主要包括数学知识的来龙去脉、纵横联系以及背后的精神、思想和方法等）、教材的编排结构，以及学生已有的认知基础、认知经验，这样才能帮助学生在进一步的学习中不断丰富和发展自己的数学认知结构。

例如，苏教版小学数学教科书四年级下册“用数对确定位置”一课，在数学知识自身结构上，用有序数对确定物体的位置是点的坐标的雏形，而坐标的概念则是解析几何的基本概念，解析几何不仅是创立微积分的基础，又与微分几何、高维空间几何等有着密切联系，它们共同构成坐标几何体系；在教材编排结构上，学生在一、二年级已经学习了“上、下、左、右、前、后”以及“第几排第几个”等相关知识，这里是在此基础上学习“用数对表示物体的位置”，而将来到了中学则要学习通过建立直角坐标系来研究图形的位置与运动；从学生的认知基础和认知经验来看，学生不仅具有上述一、二年级学习的相关书本知识，在日常生活中学生已经具有用数对确定物体的经验，如确定教室、电影院里的座位等。

尊重儿童

现代认知心理学认为，学生学习数学的过程实际上是一个数学认知的过程，在这个过程中学生在教师的指导下，把数学知识结构转化成自己的数学认知结构。奥苏伯尔提出，有意义学习过程的实质，就是符号所代表的新知识与学习者认知结构中已有的适当观念建立非人为的（nonarbitrary）和实质性的（substantive）联系。

“非人为的”联系，即新知识与认知结构中有关观念在某种合理的或逻辑基础上的联系。在数学知识的学习问题上，“非人为的”的联系一般是依托数学知识自身的结构来实现的，前面已经有所论述。例如教学“分数的再认识”时，通过让学生讨论分数“是什么”、“怎么做”、“为什么”的教学环节，使学生体经历了分数概念的“再创造”的过程后对整个过程进行梳理和反思，充分实现了新知识和学生已有认知结构的非人为的联系。“实质性的”联系，是指新的符号或符号所代表的观念与学习者的认知结构中的已有的表象、已经有意义的符号、概念或命题的联系。在“分数的再认识”的新课教学时，先引导学生思考“以领带度量沙发长时，沙发没有一个领带长，怎么办呢？你有办法吗？”学生得出“用分数来表示”的结论，这是因为学生在三年级已经学习了“分数的初步认识”，虽未形成真正意义上的分数概念，却已经具有分数的“前科学概念”。很快，学生就得出“沙发是7／8个领带长”。

除了要依据学生的认知基础和认知经验教学外，我们还要尊重学生的思维发展水平，依托学生的思维水平改善我们的教学实施。例如教学苏教版四年级上册“可能性”一课时，就得关注儿童的思维能力。皮亚杰和印海德（Piaget＆ Inheldel，1975）的研究表明，7 岁以前的儿童尚无法区分事件的必然性与可能性；7～14岁儿童已能认清事件的必然性与可能性，但无法系统地产生一系列关于概率的概念。四年级学生基本处于9～10岁，也就是说开始具有区分简单事件的必然性与可能性的能力，但是这个能力还不是很稳定，需要不断强化发展。

整体把握

审视课标、审视教材、尊重知识、尊重儿童，这些都是实现对当前小学数学教学的认识和超越的重要视角。我们在具体教学实践中，要从整体上去把握这四个不同的层面，它们既有区别又彼此联系，并统一于小学数学教学的理论研究与教学实践之中。一方面，我们从文本的视角研究课标和教材时，要深入思考文本背后所蕴含的哲学思想、教育理论、教学原理和方法，实现文本认知到理性思考的超越；另一方面，我们不仅要对作为文本的课标和教材进行认识和审思，更要对文本之外的数学本体知识和儿童现实作出深刻把握。简言而之，遵循教育的本义、数学的本质和儿童的本性，永远是小学数学教育研究与教学实践的应然取向。