在解决问题中有效渗透模型思想

江苏盐城市第一小学（224000） 邵伟丰

在数学学习中，构建数学模型是解决问题的重要环节，教师要灵活渗透模型思想，引导学习者体验建模过程，学会由实际问题情境中发掘蕴含的数学模型，会用数学语言来描述现实原型。那么，在小学数学教学中，教师该如何在解决问题中有效渗透模型思想，提高学生解决问题的能力呢？对此，笔者提出了如下建议，以供参考。

一、引入情境，逐步感知

由数学新课程来看，在教学过程中，教师需要以学习者已具有的生活体验与经验为出发点，使其参与把实际问题合理抽象转化为数学模型并且应用数学知识来解释与解决实际问题的过程，加深对知识的理解与印象，也培养学生各方面的能力，升华情感。另外，由生活实际引出问题，有助于培养学生以数学眼光来看待问题，将生活原型上升到数学模型，初步感知数学模型。

所以，在小学数学教学中，进行建模活动时，教师要由学生比较熟悉的日常生活背景中合理选取贴近他们实际水平的、富有探究性的学习素材，设置真实自然的学习情境，诱导学生发掘情境中、生活中蕴含的数学问题，提炼信息，形成数学模型意识。如教学“解决问题的策略”时，课本中展示了2杯果汁的数学主题图（如图1所示），提出的问题是：原先甲乙2杯果汁分别是多少毫升？主题图虽然简单却隐含着丰富信息，引导同学们观察与思考后，他们可提炼出关键信息：现在两杯果汁同样是200毫升。这样，通过展示生活化情境，激活学生生活经验，促其发掘数学问题，分析与提炼出有用信息，给后续解题中形成思路与策略、构建数学模型打好坚实基础。

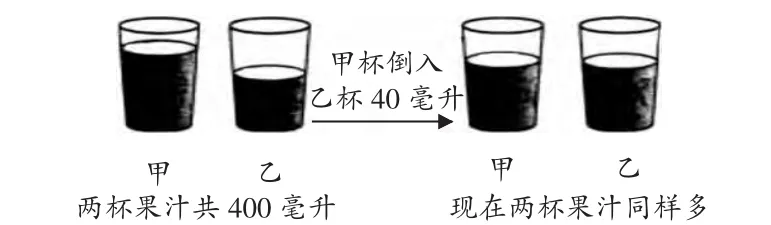
图1

二、引导发现，形成策略

在小学数学教学中，面对所给情境，产生数学问题，形成建模雏形后，还要认真分析多种因素，探寻主要因素，并对其展开抽象与综合，形成解题策略，建立正确的数学模型，化繁为简。但在具体解题过程中，不少学生在粗略浏览题目后，便急于列算式计算，由于缺少数学化过程，面对复杂问题情境时，学生就容易陷入思维困境，出现解题困难与错误。所以，教师还要引导学生经历分析、比较、抽象、综合等思维过程，提炼相关数量，发现有关联系，感悟解决问题的策略，有效建立相应数学模型。

例如：四边形ABCD是正方形（如图2所示），A是圆心，四边形ABCD的面积S正＝10cm2，请求出圆的面积。

图2

有的同学习惯性的根据S圆＝πr2的数学公式进行套算，但却不能算出半径的值。这时，教师提问引思：求圆的面积除了给出r、d或周长c的条件之外，是否还可以用其他已知条件来求解？引导学生再次审视圆的面积公式，意识到已知r2即正方形面积也能求解。而后继续因势利导，促其探寻解题突破口，形成思路与策略，提炼数量关系式，建立数学模型：以正方形的某个顶点为圆心，以正方形边长为半径的圆的面积等于πS正。

三、建模应用，解决问题

在小学数学教学中，渗透模型思想的最终目的在于让学生发掘问题本质，探寻规律，能够灵活建立与运用数学模型来分析与解决实际问题，沟通现实生活与数学的联系，做到学以致用，而不单单是通过提炼概括而建立的数学模型。所以，在小学数学教学中，教师还需要选取生活化问题，指导学生展开深层探究，用自己的语言来表述解题过程，分享解题经验，更好地形成解题策略，深化模型思想。

例如：现有一块正方形钢板，已知其面积S＝40dm2，从中截取一块最大的圆形钢板，请求圆形钢板的面积。（如图3所示）。结合前面的图2，可以看出图3所示的大正方形是图2所示的小正方形变大而成的，进行逆向思维，则可以发现图3中的大正方形中隐藏了一个与图2中类似的小正方形（如图4所示），可以求解出S圆＝

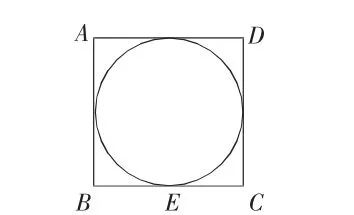
图3

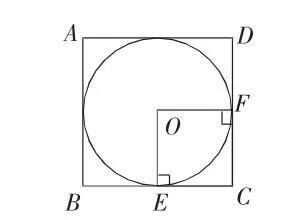
图4

总之，教师要善于让学生从现实情境、生活问题等表象中抽象概括出数学模型，学会迁移运用，提高学生思维能力、解题能力，为今后的学习奠定良好基础。