基于ANSYS的直流电磁铁温度场仿真分析

， 　， 　，

(1.西北工业大学 航天学院， 陕西 西安　710072； 2.西安航天动力研究所， 陕西 西安　710100)

引言

液体火箭发动机的推进剂供应系统中大量使用电磁阀作为开关执行元件，控制推进剂供应的开启和关闭，实现发动机的多次重复启动和脉冲工作，电磁阀的性能和可靠性对液体火箭发动机的工作可靠性有着重要影响。在电磁阀通电工作过程中，电磁铁线圈发热量大且散热条件差是一个突出的问题。线圈温升过大，不仅会影响电磁阀响应速度等使用性能，严重时会造成线圈绝缘性能降低，甚至出现匝间击穿、短路，以致烧毁。

在电磁阀的实际工程研制中，通常利用经验公式校核初步设计的电磁阀结构是否满足温升要求，这种计算方法往往具有一定的经验性和不确定性，所以，在电磁铁的工程设计中，能够较准确的预估其通电工作时线圈的温度和电磁铁其它部分的温度场分布具有重要的意义。在以往文献中利用ANSYS有限元软件对电磁铁温度场进行仿真时，加载的热载荷和边界条件都是定值，并通过调节散热系数的方法计算出与实际情况相符的结果，实际应用中如果不能准确的预估热载荷和散热系数，将不能得到准确的结果。本研究对以往计算方法进行改进，考虑热载荷和边界条件随时间的变化，基于ANSYS Workbench平台对某型发动机控制阀电磁铁温度场分别进行稳态计算和瞬态计算，并进行电磁铁线圈发热试验。

1　ANSYS热分析基本理论

1.1　热平衡方程

热分析用于研究结构在热载荷下的热响应，其理论基础是基于傅里叶定律的热传导方程。在ANSYS程序中，热分析主要包括稳态热分析和瞬态热分析。

如果系统的净热流率为0，即流入系统的热量加上系统自身产生的热量等于流出系统的热量，则系统处于热稳态，在稳态热分析中任一节点的温度都不随时间的变化而变化，根据能量守恒原理，稳态热平衡方程可以表达为：

[K]{T}={Q}

(1)

式中, [K]为热传导矩阵，包含导热系数、对流系数及辐射率和形状系数；{T}为节点温度向量；{Q}为节点热流率向量，包含热生成。

ANSYS程序是利用模型几何参数、材料属性参数以及所施加的边界条件，生成[K]、{T}及{Q}。

瞬态传热过程中系统的温度、热流率、热边界条件以及系统内能随时间都有明显变化，瞬态热分析的能量平衡方程为：

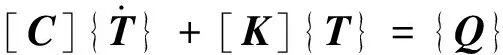
(2)

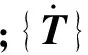
1.2　边界条件

热分析中为了使节点的热平衡方程具有唯一解，需要附加一定的边界条件和初始条件，热分析中一共有三类边界条件。

第一类边界条件是指物体边界上的温度函数为已知，用公式表示为：

TΓ=f(x,y,z)

(3)

式中, Γ为物体边界；f(x,y,z)为温度函数(随时间位置而变)。

第二类边界条件是指物体边界上热流密度为已知，用公式表示为：

(4)

式中,λ为导热系数，W/m·℃；g(x,y,z)为热流密度函数(随时间位置而变)。

第三类边界条件是指与物体相接触流体介质的温度Tf和热交换系数α为已知，用公式表示为：

(5)

式中，Tf和α可以是常数，也可以是随时间和位置变化的函数。

2　电磁铁温度场稳态计算

电磁铁线圈通电工作时，由于线圈电阻产生的焦耳热会使电磁铁各部分的温度逐渐升高，在某一时刻，线圈生成的热量等于电磁铁所有部分散发的热量，此时电磁铁温度场每一点的温度不随时间变化，电磁铁温度场处于热稳态。本研究首先对电磁铁温度场进行稳态热计算，得到稳态情况下的电磁铁温度场分布规律。

2.1　电磁铁有限元模型

1) 三维物理模型的建立

本研究所分析的螺管式电磁铁具有轴对称结构，为了提高计算效率，只需建立四分之一的模型。图1所示为在Ansys Workbench平台下建立的某型电磁铁三维实体模型和网格划分结果。

图1　电磁铁三维模型及网格划分结果

对电磁铁的温度场进行稳态计算只需要定义的材料属性是热传导率，表1所示为电磁铁中各部分材料的热传导率。需要说明的是，材料的热传导率随着温度的变化而变化，但由于电磁铁通电工作时温度一般相对较低，而且变化范围较小，对材料热传导率的影响有限，从而可以忽略温度对材料热传导率的影响。

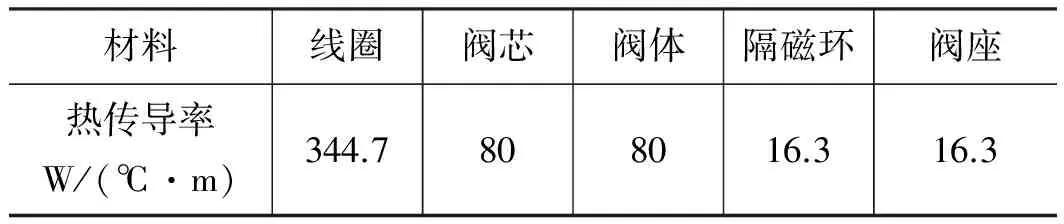
表1　材料热传导率

2) 载荷及边界条件的确定

电磁铁工作时，通电线圈由于电阻损耗的作用产生焦耳热，起到内热源的作用，所以在温度场稳态计算中，把线圈部分的生成热作为热载荷。在以往文献中利用ANSYS有限元软件对电磁铁温度场的仿真计算中，线圈的热生成功率都是取恒定值，这个恒定值一般是线圈工作过程中的平均发热功率，线圈平均发热功率的取值带有很大的经验性，从而影响了电磁铁温度场计算结果的准确性。

在电磁铁实际工作过程中，在工作电压不变的情况下，线圈的电阻值随着温度的增加而增加，从而线圈的发热功率随着温度的增加而降低。如图2所示为线圈的发热功率随时间的变化曲线，仿真模型里把线圈的发热功率除以线圈体积得到的生热率加载到线圈上。

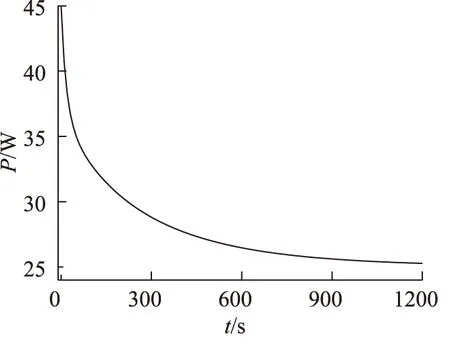
图2　线圈发热功率随时间变化曲线

边界条件的确定也是影响温度场计算准确性的重要因素，对于本研究的螺管式电磁铁的边界条件主要是和空气之间的对流散热系数。根据参考文献[3]得到的结论，线圈表面的散热系数可由公式(6)确定，把散热系数和温度之间的关系加载到电磁铁散热表面。

(6)

式中,kt为线圈表面的综合散热系数，W/(m2·℃)；S为线圈散热面积，cm2；θp为线圈每一时刻的温度，℃；θ0为环境温度，℃。

2.2　计算结果及分析

根据以上材料属性、热载荷和边界条件，对电磁铁进行稳态热计算，由于加载的热载荷和边界条件都是随着时间和温度变化的，所进行的热计算是非线性的，计算需要的时间也会长一些，最终得到的电磁铁稳态温度场分布云图和热梯度矢量图如图3所示。

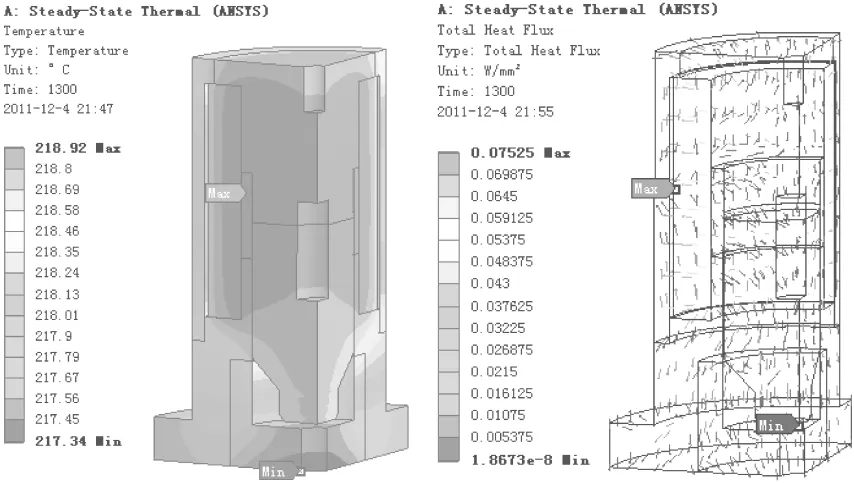
图3　电磁铁温度场分布云图及热梯度矢量图

从图3电磁铁温度场分布云图可以看出，电磁铁线圈部分温度最高，这是由于线圈部分起内热源的作用，远离线圈的阀体温度相对较低。从电磁铁温度场的具体数值可以看出，电磁铁所有部分的温度相差较小，这是由于线圈直接绕在阀体上，而且电磁铁各部分都是导热性能良好的材料，在稳态计算的条件下，温度相差必然会很小。利用ANSYS有限元软件进行稳态计算得到的线圈稳态温度为218.9 ℃，线圈发热试验中线圈的温度最终稳定在216.8 ℃左右，这说明利用ANSYS有限元软件对电磁铁温度场进行稳态计算，可以得到较为准确的结果，但前提是所加载的热载荷和边界条件合适。

3　电磁铁温度场瞬态计算

为了得到电磁铁通电工作时每一时刻的温度场分布规律，下面对电磁铁温度场进行瞬态计算。电磁铁温度场的瞬态计算和稳态计算的物理模型、热载荷和边界条件都相同，不同之处是瞬态计算中不仅需要定义材料的热传导率，而且需要定义材料的密度和比热容，如表2所示电磁铁各部分材料的密度和比热容。另外，瞬态计算中需要设置计算结束的时间及时间步长。

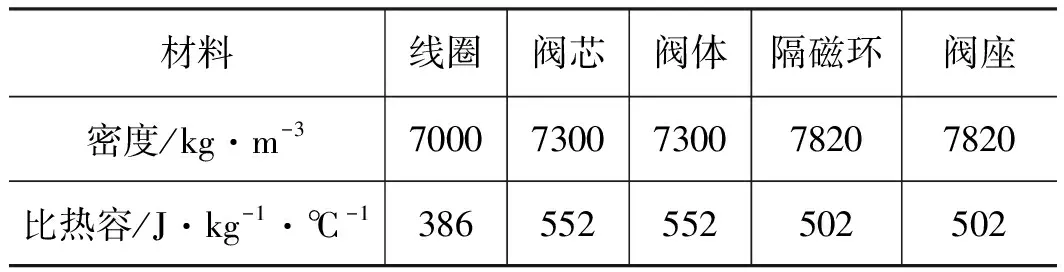
表2　材料属性

对电磁铁温度场进行瞬态计算，设置计算结束时间为1200 s，时间步长为60 s，图4～图5所示为60 s时刻和120 s时刻电磁铁温度场分布云图及热梯度矢量图。从图中可以看出，每一时刻线圈部分的温度最高，和线圈直接接触的部分由于金属导热的作用温度也较高，离线圈较远的地方温度较低。电磁铁通电工作60 s和120 s时， 线圈的瞬态温度分别为98.8 ℃和121.5 ℃，线圈发热试验得到的结果分别是98.3 ℃和122.3 ℃，这说明ANSYS瞬态计算可以较为准确的得到电磁铁每一时刻的温度场分布规律。

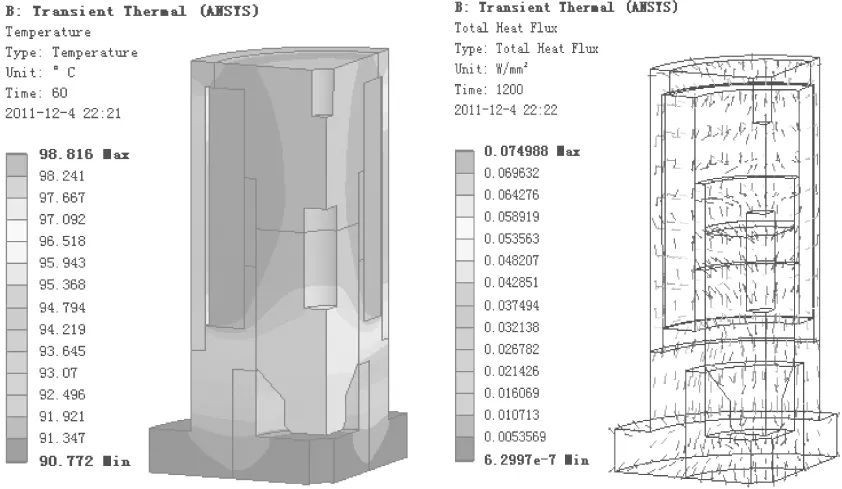
图4　60 s时刻温度场分布云图及热梯度矢量图

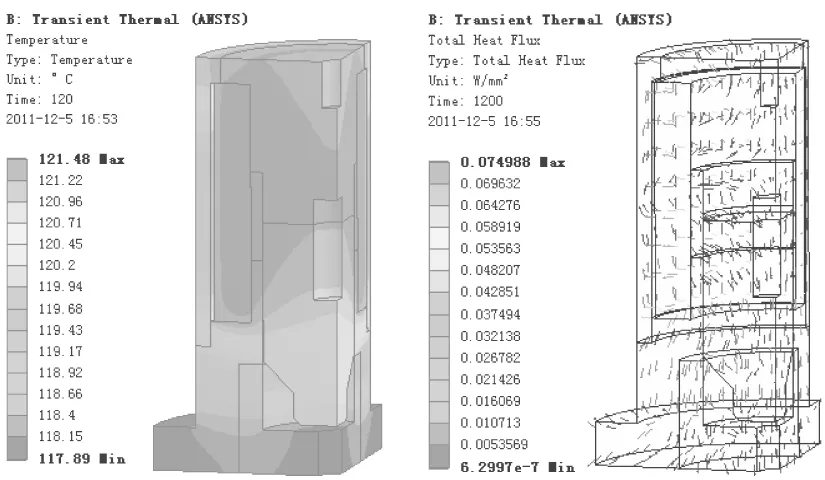
图5　120 s时刻温度场分布云图及热梯度矢量图

图6中计算曲线所示为线圈部分的温度随时间的变化曲线，从图中计算曲线可以看出，线圈温度随时间呈指数形式增长，符合实际情况，这是由于在利用ANSYS 对电磁铁进行数值计算时，所加载的热载荷和边界条件都是随温度和时间非线性变化的。在以往文献中的类似问题，由于加载的生热率和散热系数都是定值，最终得到的温度随时间的变化曲线都是线性的，这不符合实际情况。从图中还可以看出，线圈的温度最终基本稳定在219 ℃左右，这和稳态计算结果相符。

4　试验验证及分析

为了验证基于ANSYS的电磁铁温度场仿真结果的正确性，对电磁铁线圈进行发热试验。线圈温升一般采用电阻法测量，电阻法测量温升的原理是被测电磁铁线圈的电阻值随线圈温度的升高而线性增加。试验中给线圈接通直流电压，每隔1 min测量一次线圈电流，然后根据欧姆定律求得线圈每一时刻的电阻值R2，每一时刻线圈温升θ按下式计算：

(7)

式中,θ为线圈温升，℃；R1为0时刻线圈电阻，Ω；R2为线圈通电后每一时刻电阻，Ω；θ0为发热试验开始时环境温度，℃；θ2为线圈通电后每一时刻的温度，℃。

图6所示为基于ANSYS有限元软件计算得到的线圈温升曲线和试验结果对比图。从图中看出，线圈通电刚开始一段时间内，温升上升的较快，线圈通电10 min以后，线圈温升上升缓慢，总体上计算曲线和试验曲线基本吻合。试验结果验证了基于ANSYS有限元软件建立的温度场仿真模型和仿真结果的正确性，表明基于ANSYS有限元软件够准确的计算出线圈温升随时间的变化规律。

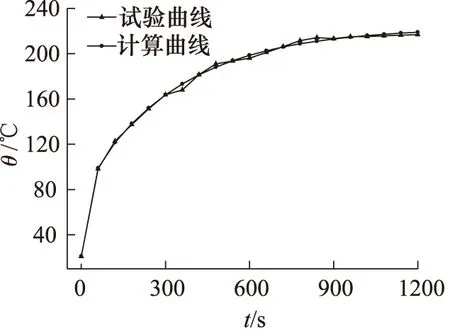
图6　线圈温升曲线对比

5　结论

基于ANSYS有限元软件对电磁铁温度场进行了仿真，仿真模型中，考虑了热载荷和边界条件随时间的变化，改进了以往文献中利用ANSYS有限元软件计算电磁铁温度场的方法，使得仿真结果更加准确。对电磁铁进行了线圈发热试验，试验结果表明本研究建立的电磁铁温度场仿真模型能够准确的计算出线圈温度随时间的变化规律。利用ANSYS有限元软件不仅能够计算电磁铁线圈温度随时间的变化，而且能够清晰、直观的反映出电磁铁整个温度场的分布规律，为研究电磁铁热性能和提高电磁阀的工作可靠性具有一定的工程应用价值。

参考文献：

[1]王宝龄.电磁电器设计基础[M].北京:国防工业出版社，1989.

[2]朱宁昌，刘国球.液体火箭发动机设计[M].北京：宇航出版社，1994.

[3]王春民，沙超，魏学峰.直流螺管式电磁阀线圈温升研究[J].液压与气动，2014,(8)：60-63.

[4]李继山，林祜亭，李和平.基于ANSYS电空制动EP阀线圈稳态温升的研究[J].铁道机车车辆，2005(4)：28-29.

[5]Richard L Huftalen. Next Generation Propellant Isolation Valve Design and Development[R].USA:AIAA,2006：2006-4879.

[6]林抒毅，许志红.交流电磁阀三维温度特性仿真分析[J].中国电机工程学报，2012,32(36):156-163.

[7]黄琳敏，陈德桂.应用瞬态热路法计算直流电磁铁的温升[J].低压电器，2003,(2)：12-15.

[8]王晓峰，唐武进，耿英三.利用ANSYS软件进行直流螺管式电磁铁温度场分析[J].电机电器技术，2002,(6)：45-47.

[9]赵凯华， 陈熙谋. 电磁学[M]. 北京：高等教育出版社， 2003.