基于ReliefF算法和相关度计算结合的故障特征降维方法及其应用

， ， ， 　

(1.燕山大学 河北省重型机械流体动力传输与控制重点实验室， 河北 秦皇岛　066004；2.燕山大学 先进锻压成形技术与科学教育部重点实验室， 河北 秦皇岛　066004)

引言

旋转机械的故障诊断[1]就是在设备不解体的情况下，研究故障的外在表现与故障本质的联系，进而根据外在信息判别出故障的类型。在分类问题中，决定一个样本属于哪一类的所有信息都应包含在描述该样本的特征向量中[2]。为了对旋转机械进行故障诊断，必需提取与旋转机械工作状态相关的特征信息。为了使获取的样本含有大量的故障信息，通常从时域、频域和时频域选取特征指标，形成具有众多特征参数的原始特征向量，实现模式到特征的转换。然而，维数过高不仅会使计算量按指数级增长，导致“维数灾难”问题；而且，由于众多特征中存在很多冗余的、与分类不相关的甚至会对分类产生干扰的特征，识别效率反而会下降[3]。因此，有必要对原始各特征的分类能力进行评价，选择出分类能力强的特征，剔除无效的和冗余的特征，以降低特征向量的维数，从而简化分类器的设计。

为此，本研究采用ReliefF加权特征选择算法对原始特征向量进行特征选择，去除对分类无效的特征，保留分类能力较强的特征；再结合特征相关度算法从保留的特征中剔除冗余特征，用剩余的有效特征组成最终的降维特征向量进行故障分类，实现故障特征的降维。

1　原始特征向量的提取

在幅值域上评价信号特征的指标有两类，第一类是有量纲特征参数，主要包括：均值、峰值、均方根值、方根幅值、斜度、峭度等；第二类是无量纲特征参数，主要包括：波形指标、峰值指标、脉冲指标、裕度指标、峭度指标等。这些特征参数可直接用于设备状态的在线监测，也可作为其他诊断方法的特征参数，用于辅助诊断。

(1)

xp=maxxi

(2)

(3)

(4)

(5)

(6)

上述参数都具有明确的物理意义，例如均值指标代表信号的直流分量；峰值代表信号的最大幅值，常用于表征信号的强度；均方根值主要反映信号的平均功率的大小；峭度通常对信号的冲击成分敏感，当旋转机械发生故障时都会由异常元件产生冲击信号，这时峭度指标会有很大变化。

上述有量纲参数不仅对设备故障敏感，而且还依赖于外部因素(如转速、负荷状态等)的变化，所以将它们直接用于故障诊断效果不够理想。而无量纲参数能够克服上述有量纲参数的缺陷，受外部因素影响较小，所以通常作为诊断的特征参量[4]。幅值域无量纲参数主要有峰值指标Cf、脉冲指标If、波形指标Wf、裕度指标Lf和峭度指标Kf。它们的计算公式如下：

(7)

(8)

(9)

(10)

(11)

峰值指标和脉冲指标对冲击信号较敏感；裕度指标对磨损程度较敏感。峭度指标对冲击振动灵敏度较高，但它与故障的关系并不稳定，故障发生的早期，它的值会显著增大；但当故障发展到一定程度后，它的值反而减小。

由于不同故障的振动信号其小波包分解后的子带能量的分布不同，因此将旋转机械振动信号进行小波包分解并分析各子频带的能量分布情况，可从中提取出具有分类意义的重要信息[5]。

小波包子带能量的计算步骤为：

(1) 对所要分析的信号进行M层小波包分解，得到2M个子频带的分解系数；

(2) 对各个子带的分解系数进行重构，即可提取原始信号中第M层从低频到高频共2M个子带信号。各子带重构信号分别记为s1,s2,…,si,…,s2M；

(4) 将各子带能量进行归一化处理，可得到子带归一化能量的分布：

Ti=Ei/E,i=1,2,…,2M

(12)

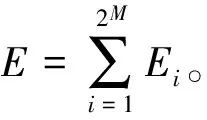
2　原始特征向量的特征降维

2.1　基于ReliefF算法的特征选择

单词relief是缓和、减轻的意思，用在特征选择方面就是指把高维降到低维。Relief算法[6]是Kira等于1992年提出的，只适用于两类分类问题。为了处理不完整数据问题，Kononerko[7]将其扩展，相继提出了ReliefA、ReliefB、ReliefC、ReliefD算法。为了处理多类分类问题他又提出了ReliefE、ReliefF算法。Relief系列算法是一种依据权重选择特征的方法，能够选出那些与类别相关性强的特征，去掉无效的特征以降低原始特征向量的维数。

ReliefF 算法具体实现步骤如下：

输入：训练样本集D(m×n)，由m个样本构成，每个样本由n个特征A1,A2,…,Al,…,An表示；输出：特征权值向量w(1×n)，w(Al)表示特征Al的权值。

(1) 设置向量w初始值为零向量；循环次数为r，r≤m；样本集D中样本类别号为c，c为大于等于2的正整数。

(2) fori= 1 tor：

ⓐ 从样本集D中随机挑选出一个样本Ri；

ⓑ 在Ri的同类中找出与Ri最近邻的k个样本Hj，j=1,2,…,k；

ⓒ 在Ri的每个不同类中找与Ri最近邻的k个样本Mj，j=1,2,…,k；

ⓓ forl= 1 ton，对于每个特征权值进行如下更新：

(13)

式中，class(Ri)表示样本Ri的类别号。

(3) 输出特征权值向量w。

对于某维特征Al，若它有利于分类，则应使同类样本接近而使其异类样本远离。权值更新公式(13)便遵循这一原则设计，即来自同一类别的两样本在特征Al上的距离 diff(Al,Ri,Hj)越小，并且来自不同类别的两样本在特征Al上的距离diff(Al,Ri,Mj)越大，其获得的权值w(Al)就越大。

式中，P(c)是第c类样本数占样本总数的比例，即：

(14)

diff(Al,S1,S2)表示两个样本的欧氏距离，用来度量两样本的相异度，它的计算方法如下：

对于离散特征：

(15)

对于连续特征：

(16)

式中，S1，S2是两个样本，value(Al,S1)是样本S1在特征Al处的值。

为了去掉对分类无效的特征，把特征按照权值的大小进行排列，然后把权值高于设定阈值的那些特征挑选出来，摒弃其它权值较小的特征，用挑选出来的特征构成新的特征子集，便完成特征选择过程。

2.2　基于特征相关度计算的冗余特征剔除

经ReliefF算法选取的特征子集都是与类别具有较强的相关性。但由于ReliefF算法并没有考虑特征之间的相关性，所以所选特征中难免存在冗余特征。为了从中剔除分类能力接近的冗余特征，可通过特征相关度算法来实现。本研究采用Pearson积矩相关系数公式[3]剔掉分类能力接近的冗余特征。

假设样本集D中有N个样本，x和y是两个特征变量， N个样本的x和y的取值分别为xi和yi， 其中i=1,2,…,N。Pearson积矩相关系数公式如下：

(17)

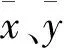
相关性系数的取值范围为[-1，+1]。当相关系数小于0时，称为负相关；大于0时，称为正相关；等于0时，称为零相关。r(x,y)的绝对值越大，x的变动引起y的变动就越大。r(x,y)>0.8时为高度相关，当r(x,y)<0.3时为低度相关，其它情况下为中度相关。

通过上述论述可知，将ReliefF算法和特征相关度计算结合，可以去除对分类无效和冗余的特征。本研究先用ReliefF算法计算出每个特征的权值，按降序排列，然后选出使故障训练样本集故障诊断正确率大于95%的前几个特征，再用相关度计算公式分别计算这几个特征的相关性系数，对于相关性系数大于0.8的两个特征剔除其中权值较小的一个。

3　基于ReliefF算法和相关度计算结合的故障诊断

3.1　故障原始样本的获取

实验分析所用信号为某液压泵状态监测与故障诊断系统中采集的斜盘式轴向柱塞泵振动信号与机械故障综合模拟实验台(MFS-MG)上采集的轴承振动信号。液压泵故障振动信号采集系统如图1所示，液压泵额定转速为1470 r/min，实验中采样频率为50 kHz。轴承故障模拟实验台如图2所示，电机转速调定为1800 r/min，轴承振动信号采样频率为50 kHz。

由于旋转机械的振动信号通常存在调制现象，并且叠加强噪声，所以首先要对实验采集的原始振动信号进行解调和消噪预处理，然后提取原始故障特征向量。

振动信号进行解调和消噪预处理的过程： 对采集的振动信号，使用小波包频带能量分析确定共振频带，并完成带通滤波和消噪；接着采用Hilbert包络解调法对经带通滤波和消噪后的信号进行解调，得到包络信号[9]。由于感兴趣的故障特征频率及其前几阶高次谐波成分分布在0～1000 Hz的频率范围内，所以在信号经过解调后， 对得到的包络信号进行采样频率为2 kHz 的重采样，故重采样后包络信号的Nyquist频率为1 kHz。

图1　液压泵故障振动信号采集系统

图2　轴承故障模拟实验台

原始故障特征向量提取过程：分别提取泵和轴承正常工作及各故障状态下包络信号的幅值域无量纲特征参数(峰值指标、脉冲指标、波形指标、裕度指标、峭度指标，共计5个，分别用A1，A2，A3，A4，A5表示)、时频域特征参数(对包络信号进行3层小波包分解得到的八个子频带归一化能量，共计8个，分别用A6，A7，A8，A9，A10，A11，A12，A13表示)，构造一个 13维的特征向量。其中8个子带对应的频率范围依次为：0～125 Hz，125～250 Hz，250～375 Hz，375～500 Hz，500～625 Hz，625～750 Hz，750～875 Hz，875～1000 Hz。

依据上述信号预处理和原始特征向量提取过程，获得用于故障诊断的样本集[8]。

液压泵故障样本集由四类(正常、松靴、滑靴磨损和斜盘磨损)样本组成，每类样本200个，将其分为训练样本(每类样本100个)和测试样本(每类样本100个)。

轴承故障样本集由四类(正常状态、外圈故障、内圈故障和滚动体故障)样本组成，每类样本200个，将其分为训练样本(每类样本100个)和测试样本(每类样本100个)。

3.2　液压泵故障信号原始特征向量的降维

对于液压泵的训练样本集，在组成样本的13个原始特征中，事先并不知道哪些特征对分类有利，采用ReliefF加权特征选择算法对13个原始特征进行选择，按权值从大到小进行排列，评价结果如表1所示。

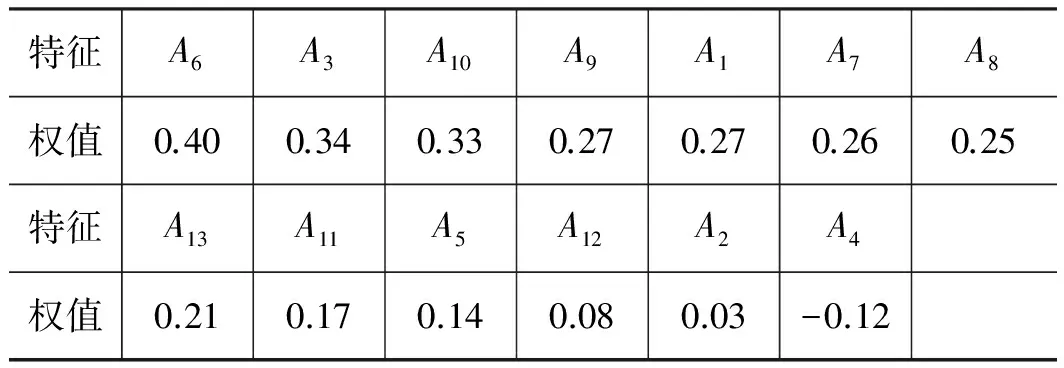
表1　液压泵故障各原始特征分类能力的权值

分析计算发现，当只选用表1中权值最高的前三个特征A6、A3、A10表示泵的故障样本集时，用K均值聚类算法进行分类，对训练样本集诊断正确率已达95%以上，所以选择出前三个特征A6、A3、A10。其中，特征A3对应波形指标，特征A6对应小波包第1子带归一化能量，特征A10对应小波包第5子带归一化能量。

由于ReliefF算法并没有考虑特征之间的冗余性，为了剔除冗余特征，实现特征进一步降维，需要进行特征相关度的计算。采用式(17)，通过相关系数计算得到，r(A6，A3) = 0.1045，r(A6，A10)=0.8974，表明特征A6与特征A3的相关性很小而其与A10的相关性较大，说明特征A10为冗余特征，因此去掉特征A10，最后选择特征A3和A6组成最终的二维特征向量。

图3为采用ReliefF加权特征选择算法对训练样本集降维后的样本分布图。

为了对比，对液压泵的训练样本集进行主元分析(PCA，Principal Component Analysis)降维，分别选取贡献率最高的前2个主元和前3个主元组成新的特征集，此时的样本分布如图4和图5所示。

对比图3、图4和图5可以说明，对于液压泵故障训练样本，ReliefF算法能够有效地评价特征的分类能力，经过特征选择和降维后，同类样本聚成一小簇，不同类样本没有交集，很好地区分了各类样本。而主元分析方法降到二维和三维时，分类效果均没有ReliefF降维算法理想。

图3　液压泵故障的训练样本分布图(ReliefF算法降维)

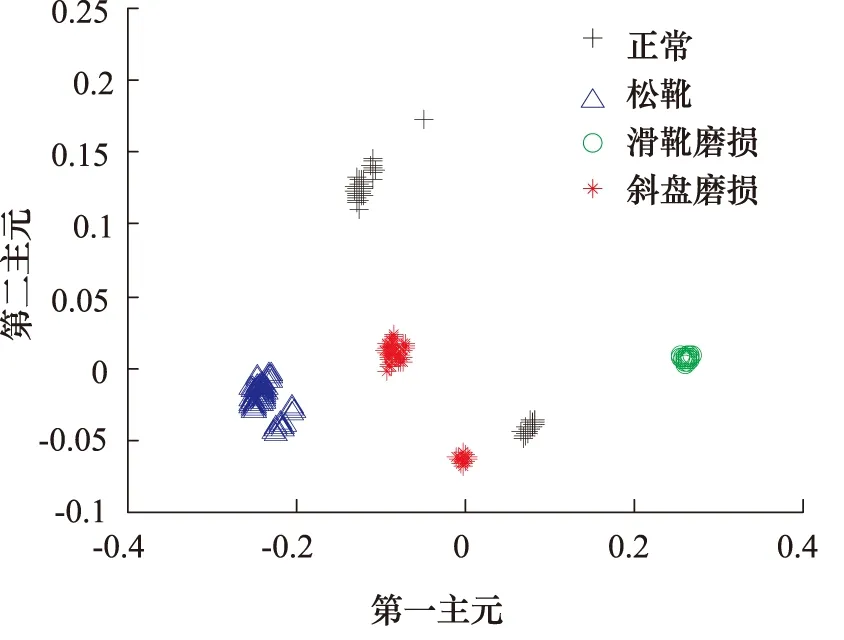
图4　液压泵故障的训练样本分布图(PCA法降到2维)

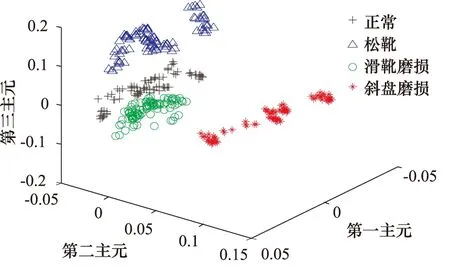
图5　液压泵故障的训练样本分布图(PCA法降到3维)

3.3　轴承故障信号原始特征向量的降维

与液压泵数据处理过程相同，对轴承的训练样本集，采用ReliefF加权特征选择算法对13个原始特征进行选择，评价结果如表2所示。

表2　轴承故障各原始特征分类能力的权值

经计算分析，用表2中权值最大的前四个特征A6、A10、A11、A8表示轴承的故障训练样本集时，诊断正确率可达95%以上，所以选择出权值最大的前四个特征A6、A10、A11、A8。通过相关系数计算得到，r(A6，A10)=0.8432，r(A6，A11)=0.8584，r(A6，A8)=0.1432，表明特征A6和特征A10、A11间有冗余，而特征A6和A8间的相关性较小，因此剔除特征A10和A11，选择特征A6、A8组成最终的二维特征向量。其中特征A6、A8分别对应小波包第1子带和第3子带归一化能量。

轴承故障特征采用ReliefF算法降维后的样本分布图与采用主元分析法降维后的样本分布图分别如图6、图7和图8所示。对比三个图可见，图6中四类样本区分效果很好，说明对轴承故障训练样本，采用ReliefF 算法进行降维比采用主元分析降维分类效果更佳。

3.4　实验结果与分析

为了验证ReliefF 算法在信号特征降维方面的优势，数据降维方法分别采用ReliefF特征选择算法和一种传统的线性降维方法-主元分析方法[11]进行对比。下面通过构造分类器对降维后的测试样本进行聚类，聚类方法采用K均值聚类算法[10]。

图6　轴承故障的训练样本分布图(ReliefF算法降维)

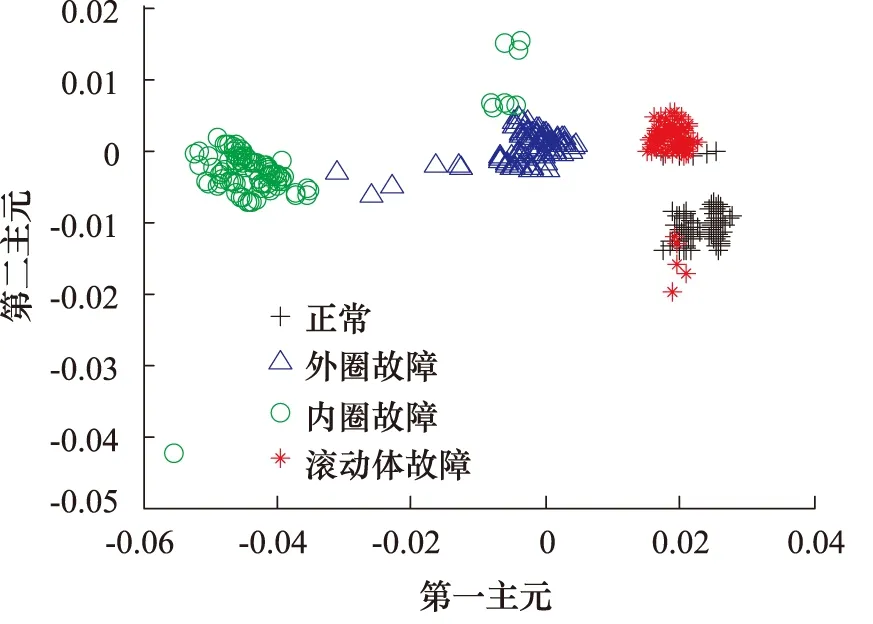
图7　轴承故障的训练样本分布图(PCA法降到2维)

图8　轴承故障的训练样本分布图(PCA法降到3维)

在对液压泵故障的样本集和轴承故障的样本集进行主元分析(PCA)降维时，分别选取贡献率较高的前2个和前3个主元组成新的特征子集。

用K均值聚类算法对分别采用上述两种方法降维后的测试样本(每种状态100个样本)进行聚类，故障识别结果分别如表3和表4所示。

表3　液压泵故障的识别结果

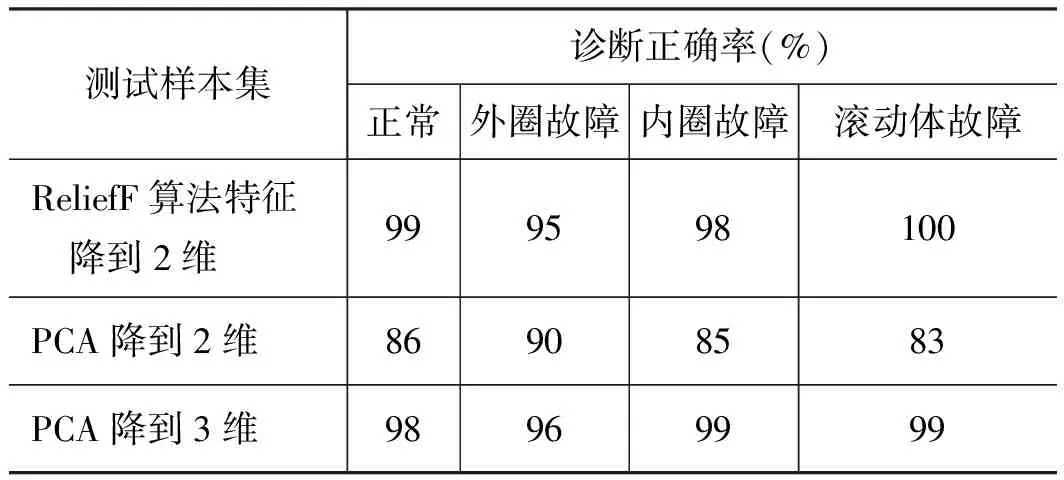
表4　轴承故障的识别结果

从表3和表4可以看出，ReliefF加权特征选择算法在液压泵和轴承数据集上产生的特征子集与传统的主元分析特征降维方法降至相同维数时相比，故障诊断正确率有了显著提高。换句话说，在保证故障诊断正确率的前提下，ReliefF算法可以降到更低的维数，有利于缩短运算时间，提高诊断效率。

3.5　本研究方法的优势

而主元分析是一种特征变换方法，可以描述成这样一个过程，对特征向量x=[x1,x2,…,xN]T施加线性变换：y=h(x)，最终产生出新的特征向量y=[y1,y2,…,yN]T，在新的特征向量中选出累计贡献率不小于85%的前k个主元组成新的特征向量y′=[y1,y2,…,yk]T，其中k

从上述描述过程可以看出，ReliefF算法特征选择较主元分析特征变换的优势有以下两点：

(1) 由特征变换产生的新特征是原有特征的线性组合，它通常只具有数学意义，一般情况下其物理含义不够明确。与此不同，ReliefF特征选择是从原始特征集中直接选出特征，并不丧失原特征的物理意义；

(2) 在多数情况下，因为从特征变换产生的特征是原始特征的线性组合，所以当用其进行故障诊断的时候，原始特征参数仍然要全部测量计算。而ReliefF特征选择后，对那些被摒弃和剔除的无效和冗余特征不再需要测量计算，只需测量计算最终被选出的那些优良特征即可，也就是在保证决策精度的前提下减少了数据处理的计算量。

4　结论

本研究提出了基于ReliefF算法和相关度计算结合的故障特征降维方法。对旋转机械振动信号首先进行包络解调并消噪，提取包络信号幅值域无量纲特征和小波包分解各子带归一化能量特征，然后通过ReliefF 算法和特征相关度算法剔除无效特征和冗余特征，选出分类能力较强的特征作为最终的识别特征进行故障诊断，实现了特征的有效降维。通过液压泵和轴承的故障诊断实验分析，结果表明：与传统的主元分析方法相比较，本方法故障诊断正确率有较大的提高，且降维后的特征保留了其原来直观的物理含义，具有广泛的工程实用价值。

参考文献：

[1]夏松波,张嘉钟,徐世昌,等.旋转机械故障诊断技术的现状与展望[J].振动与冲击,1997,16(2):5-9.

[2]刘依恋.模式分类中特征选择算法研究[D].哈尔滨:哈尔滨理工大学,2014.

[3]苏映雪.特征选择算法研究[D].长沙:国防科学技术大学,2006.

[4]姜万录,刘思远,张齐生.液压故障的智能信息诊断与监测[M].北京:机械工业出版社,2013.

[5]王冬云,张文志.基于小波包变换的滚动轴承故障诊断[J].中国机械工程,2012,23(3):295-298.

[6]Kira K, Rendell L A. The Feature Selection Problem: Traditional Methods and a New Algorithm[C]//Proceedings of the Ninth National Conference on Artificial Intelligence, Menlo Park,1992.

[7]Kononenko I. Estimation Attributes: Analysis and ex-tension of Relief[C]//The 1994 Euro-pean Conference on Machine Learning, San Francisco, USA: IEEE Press,1994.

[8]王友荣.ReliefF加权特征选择方法在旋转机械故障诊断中的应用研究[D].秦皇岛:燕山大学,2015.

[9]Jiang Wanlu, Sarah K. Spurgeon, John A. Twiddle, Fernando S. Schlindwein. Wavelet Cluster Based Envelope Demodulation Approach and its Application to Fault Diagnosis[J]. 仪器仪表学报, 2007, 28(6): 973-979.

[10]蒋帅.K-均值聚类算法研究[D].西安:陕西师范大学,2010.

[11]张煜东,霍元铠,吴乐南,等.降维技术与方法综述[J].四川兵工学报,2010,31(10):1-7.