汽车非线性液压转向系统控制策略研究

， 　(内蒙古科技大学 机械工程学院, 内蒙古 包头　014010)

引言

汽车转向系统基本要求是车轮能快速、稳定而准确地转到指定位置，所以转向系统的响应速度和稳定性对实现快速转向和安全行驶具有重要作用。一般的汽车转向系统常出现转向沉重、转向滞后、转向不稳等缺点，现在国内外主要从事电动助力转向系统和电控转向系统方面的研究，缺乏对汽车线控液压转向系统响应特性的研究，并且其作为一种新型的液压转向系统可以适用于各种路况，有着巨大优势[1-3]。本研究利用AMESim提供的HDC液压库建立了液压转向系统的模型，用MATLAB中的Simulink分别建立了模糊自适应PID控制和模糊控制模型，最后二者联合仿真，得出了油缸的位移曲线，分析出模糊自适应PID控制策略和模糊控制策略对汽车线控液压转向系统响应特性的影响。

1　非线性液压转向系统的工作原理

非线性液压转向系统的工作原理为：当方向盘转动时，转角传感器检测出相应的转角信号，传送给电子控制单元(ECU)，而ECU进行相关运算和处理，把转角信号转换成电压信号，传送给液压系统中电液比例换向阀的电磁铁，电磁铁通电时会产生推力或拉力，使阀芯运动产生相应位移，从而控制比例阀输出流量，供给液压缸，使液压缸产生相应的位移，液压缸推动着连杆机构，实现车轮转向[4]，如图1所示。

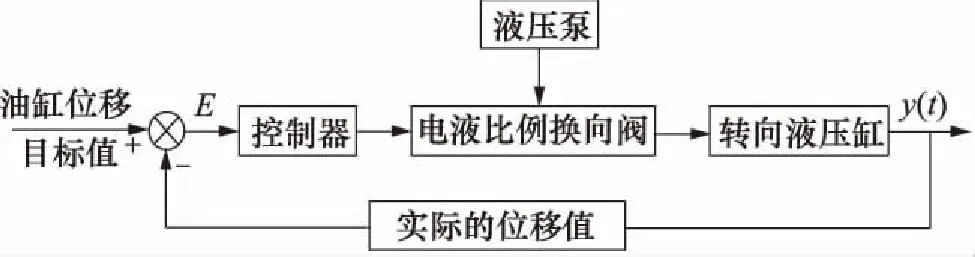
图1　非线性液压转向系统的控制原理

2　非线性液压转向系统的数学模型

对于电液比例换向阀，把线圈产生的推力简化为输入电压u的线性函数，即F=Btu,假设由阀芯运动产生的库伦摩擦力Ff为常数，其传递函数为：

(1)

式中：x—— 阀芯位移

m—— 阀芯质量

c—— 黏性摩擦阻尼系数

k—— 弹簧刚度

Bt—— 滑阀结构系数

电液比例换向阀的流量为：

(2)

假设d=const将式(2)线性化后拉氏变换得：

对于比例放大器，可简化为比例环节，其数学模型为：

(4)

式中：I(s) —— 比例放大器输出电流(A)

U(s) —— 为数字控制器输出经D/A转换成的模拟电压信号(V)

Ka—— 为比例放大器增益

综上所述，输入为电控单元的控制电压U，输出为液压缸的位移y，则以电压U为输入、缸活塞位移y为输出的三位四通电液比例阀控缸动力机构的传递函数为[5]：

式中：Kuv—— 阀的输入电压-缸运动速度增益

(m·s-1·V-1)

TR—— 电控器斜坡发生器的时间常数(s)，响应比较快的阀一般取0

TXv—— 阀芯运动的时间常数(s)

ωn—— 固有频率(rad·s-1)

ξ—— 无因次阻尼比

若去掉式中的积分环节，即可以得到以缸活塞速度v为输出的动力机构的传递函数。

3　液压转向系统的控制策略

3.1　模糊控制的仿真模型

在本液压转向系统中，可知偏差e的基本论域为[-90，90] mm，偏差变化ec的基本论域为[-10，10] mm，取输出量的基本论域均为[-6，6]。根据大量仿真得出：Ke=0.52，Kec=0.001；控制器的输入和输出的模糊论域均为{-6，-5，-4，-3，-2，-1，0，1，2，3，4，5，6}，模糊子集为：{NB，NM，NS，Z，PS，PM，PB}。为保证转向系统的快速性和平稳性，隶属函数采用三角型隶属函数。根据液压转向系统的要求，确定模糊控制规则如表1所示，模糊控制器如图2所示。

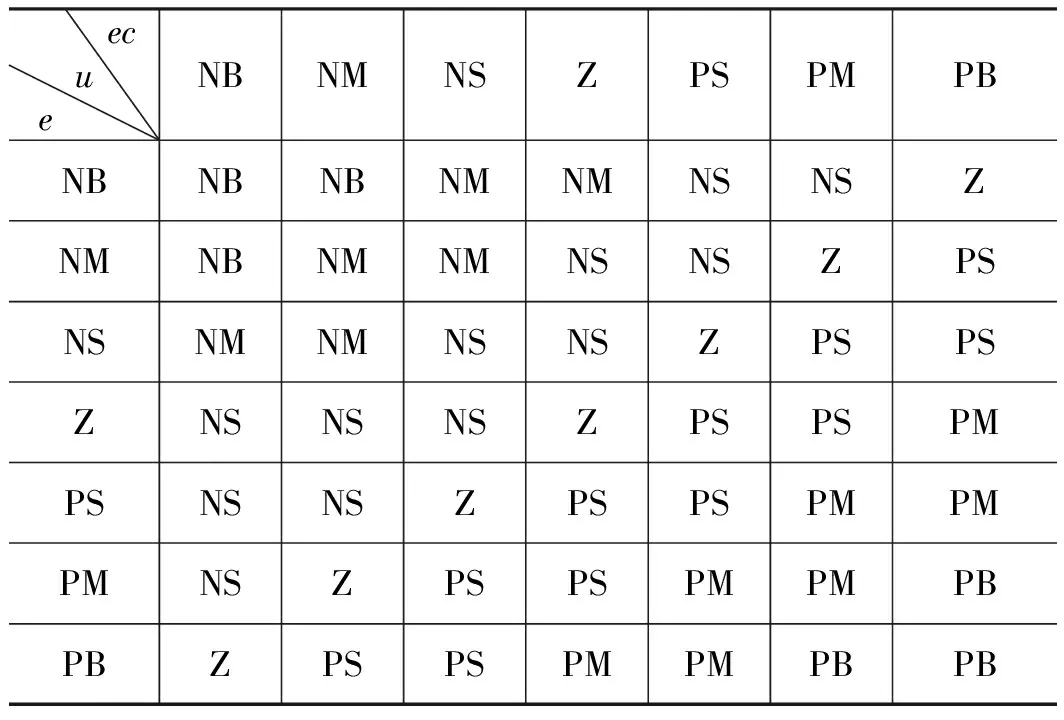
表1　模糊控制规则表

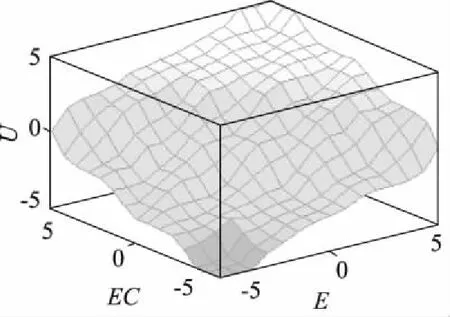
图2　模糊控制器

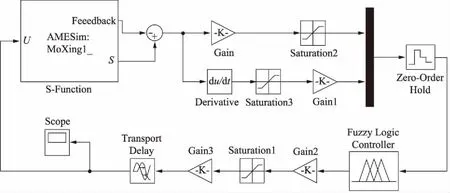
图3　模糊控制

模糊控制是建立在模糊推理基础上的一种非线性控制策略，可以控制那些不需要精确数学模型的系统，当系统负载参数变化较大时或者受到非线性因素影响时，也能取得很好的控制效果[6]。本研究根据线控液压转向系统的原理，利用MATLAB/Simulink建立模糊控制的仿真模型，如图3所示。

3.2　模糊自适应PID控制仿真模型

模糊 PID 控制器是由模糊控制器和 PID 控制器组成，偏差范围较大时利用模糊推理的方法输出控制量，实现快速且稳定的调节；在偏差范围较小时转换为PID控制，以消除稳态误差[7]。

模糊自适应PID控制的偏差e、偏差变化ec、输出量的基本论域与3.1中的模糊控制参数一样。根据大量仿真得出：Ke=0.1，Kec=0.01，Kp=3.2，Ki=0.055，Kd=0.01；控制器的输入和输出的模糊论域均为{-6，-5，-4，-3，-2，-1，0，1，2，3，4，5，6}，模糊子集为：{NB，NM，NS，Z，PS，PM，PB}。为保证转向系统的快速性和平稳性，隶属函数采用三角型隶属函数。根据转向系统的要求，确定模糊控制器如图4所示。

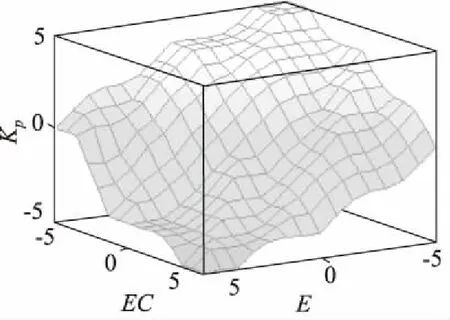
图4　模糊自适应PID控制器

根据液压转向系统的控制原理，利用MATLAB/Simulink建立模糊自适应PID的仿真模型，如图5所示。

4　液压转向系统的仿真模型

AMESim是当今领先的流体、传动系统和液压机械系统建模、仿真及动力学分析软件，其为用户提供了一个系统工程设计的完整平台，可以建立复杂的多学科领域系统的数学模型，并在此基础上进行仿真计算和深入的分析[8、9]。根据线控液压转向系统的原理，用AMESim仿真软件建立了液压系统模型，如图6所示。

5　仿真及对比分析

本研究采用AMESim和Simulink两个软件联合仿真，AMESim作为一个完整的系统工程仿真平台，MATLAB/Simulink作为一个控制系统设计的仿真平台，把二者结合起来，就能避免了不同平台之间建立模型的复杂性和重复的建立模型[8]。

5.1　阶跃信号下的仿真对比分析

输入信号为阶跃信号和液压缸的反馈信号，阶跃幅值分别设为0.05 m和0.09 m，仿真时间为3 s，得出液压缸位移(y)曲线。仿真结果如图7和图8所示。

由图7和图8可知，有、无控制都能使液压缸达到指定位置，但是从控制效果来看，控制存在着较大的差异，无控制策略使液压缸到达指定位置的时间大约是2 s左右；模糊控制使液压缸到达指定位置的时间大约是0.65 s左右；模糊自适应PID控制使液压缸到达指定位置的时间大约是0.5 s左右，比模糊控制快0.15 s，比无控制快1.5 s，所以模糊自适应PID控制明显比模糊控制和无控制响应时间短，即响应速度快，且基本无超调。

5.2　正弦信号下的仿真对比分析

输入信号为正弦信号和液压缸的反馈信号，正弦信号数据分别为幅值为0.05 m、周期为20 s和幅值为0.09 m、周期为10 s，仿真结果如图9和图10所示。

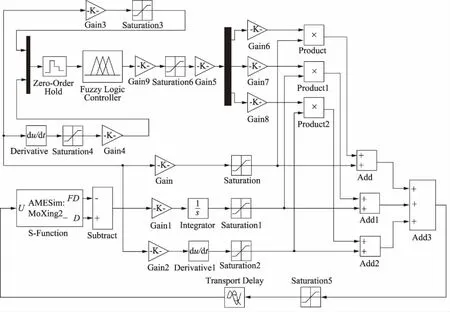
图5　模糊自适应PID控制

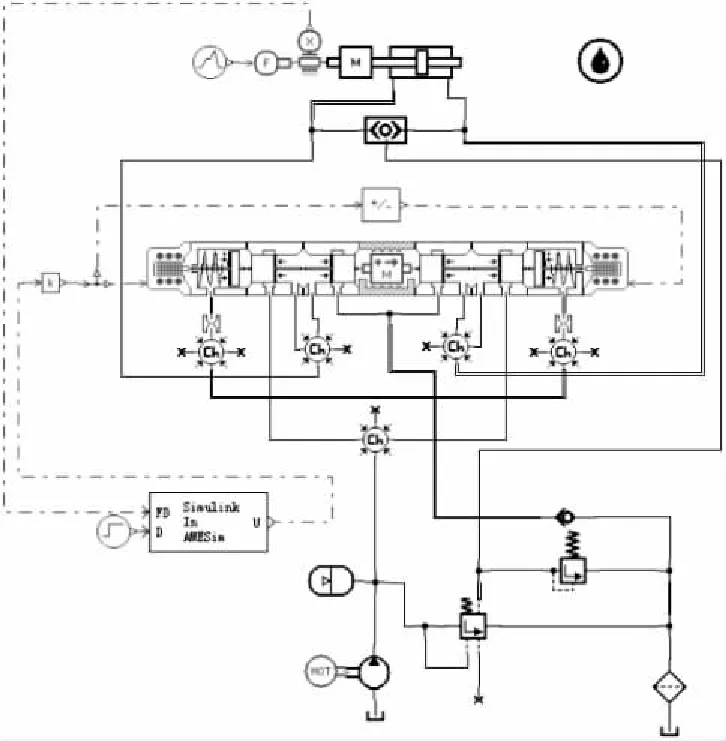
图6　液压系统模型

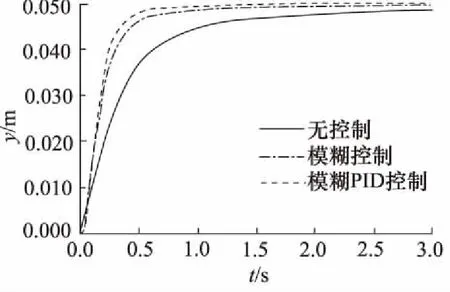
图7　幅值为0.05 m的仿真曲线对比

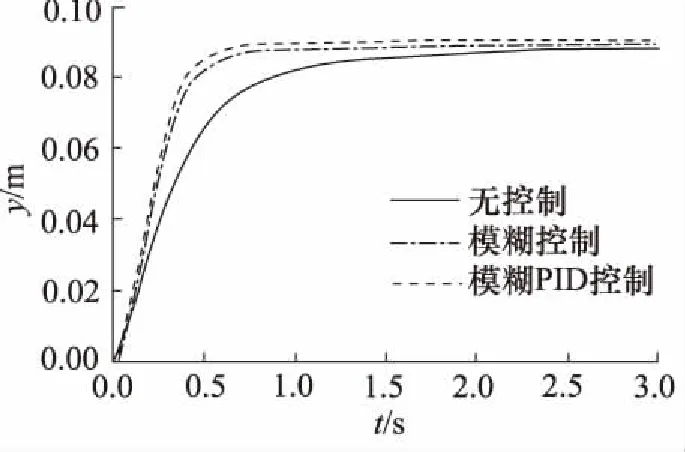
图8　幅值为0.09 m的仿真曲线对比

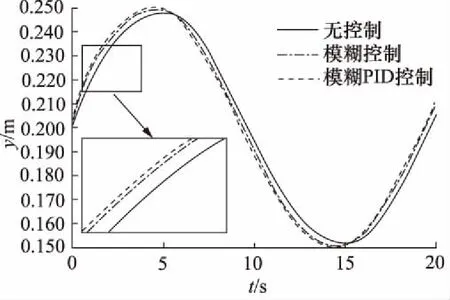
图9　幅值为0.05 m、周期为20 s的仿真曲线对比

由图9和图10可知，模糊自适应PID控制使液压缸到达指定位置的时间比模糊控制快0.3 s，比无控制快0.7 s，所以模糊自适应PID控制明显比模糊控制和

无控制响应时间短，即响应速度快，且基本无超调。

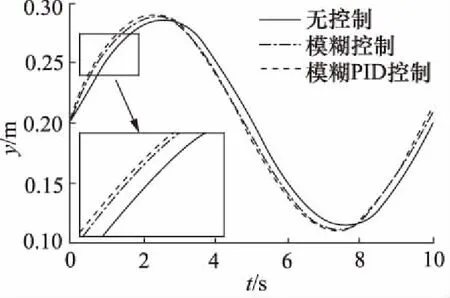
图10　幅值为0.09 m、周期为10 s的仿真曲线对比

5.3　方波信号下的仿真对比分析

输入信号为方波信号和液压缸的反馈信号，方波信号数据分别为幅值为0.05 m、频率0.05 Hz和幅值为0.09 m、频率为0.1 Hz，仿真时间分别为35 s和25 s。仿真结果如图11和图12所示。

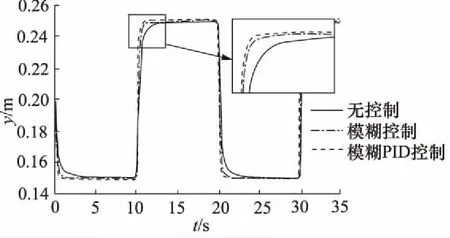
图11　幅值为0.05 m、频率0.05 Hz的仿真曲线对比

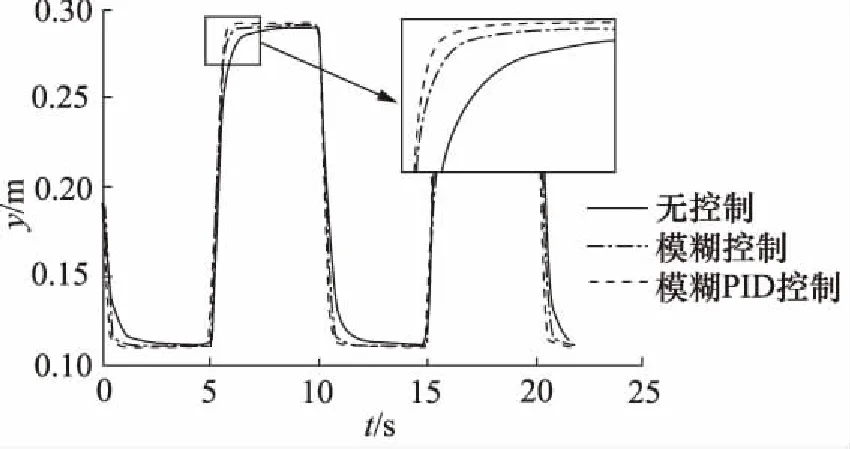
图12　幅值为0.09 m、频率0.1 Hz的仿真曲线对比

由图9和图10可知，模糊自适应PID控制使液压缸到达指定位置的时间比模糊控制快0.3 s，比无控制快1.1 s，所以模糊自适应PID控制明显比模糊控制和无控制响应时间短，即响应速度快，且基本无超调。

6　结论

研究了线控液压转向系统的响应特性，分析了在阶跃信号、正弦信号和方波信号下模糊自适应PID控制和模糊控制对系统响应特性的影响。

根据仿真分析，结果表明：模糊自适应PID控制与模糊控制相比，其响应速度大约提高了0.3 s；模糊适应PID控制与无控制相比，其响应速度大约提高了1 s左右。模糊自适应PID控制与模糊控制基本均无震荡。所以模糊自适应PID控制明显比模糊控制和无控制响应时间短，即响应速度快。对今后设计和研究新型线控液压转向系统具有指导意义。

参考文献：

[1]M K Hassan, N A M Azubira, H M I Nizam. Optimal Design of Electric Power Assisted Steering System (EPAS) Using GA-PID Method[J]. Procedia Engineering,2012,(41):614-621.

[2]Ji-Hoon Kim, Jae-Bok Song.Control Logic for an Electric Power Steering System Using Assist Motor[J].Mechatronics, 2002, 12(3):447-459.

[3]董鹏娜,李爱琴.电控液压动力转向系统的检测与故障诊断[J].液压与气动, 2012,(7):116-117.

[4]陆垚忠.基于模糊控制的线控液压转向系统的研究与实现[D].南京：南京农业大学,2010.

[5]肖体兵,肖世耀,廖辉,吴百海.三位四通电液比例阀控缸动力机构的数学建模[J].机床与液压,2008,36(8):80-82.

[6]张传红,陆静平,徐亚茹.电动助力转向系统模糊控制算法研究[J].装备制造技术,2014,(2):33.

[7]牛志刚,张建民.应用于直线电机的平滑切换模糊PID控制方法[J].中国电机工程学报,2006,26(8):132-136.

[8]江玲玲,张俊俊.基于AMESim与MATLAB/Simulink联合仿真技术的接口与应用研究[J].机床与液压，2008,36(1):148-149.

[9]Hui Cao, Hui Guo.Optimization of PID Parameters of Hydraulic System of Elevating Wheelchair Based on AMESim[J]. Procedia Engineering, 2011,(15):3710-3714.