船舶调桨液压系统大流量锁止阀设计与分析

　， ， ， 　(.同济大学 机械与能源工程学院， 上海　0804； .中船重工集团公司 上海第704研究所， 上海　0003)

引言

近年来，随着计算机和电子信息技术的快速发展，液压仿真软件朝着多学科、集成化方向发展，各种集机、电、液、热、电气和控制技术的仿真软件不断涌现，如AMESim，Hypneu和Easy 5等。液压仿真软件使得工程技术人员能够避免繁琐的代码编写和调试，但如何有效地将这些集成化的仿真软件应用于液压元器件的开发和系统设计，缩短产品研发周期，提高产品质量，仍然是困扰广大工程技术人员的问题之一。

本研究以大型船舶调桨液压系统中应用的大流量锁止阀设计为例，根据实际要求，采用仿真计算原理，建立锁止阀的仿真模型，在AMESim软件中模拟实际工况，对该阀进行计算分析，解析其静态和动态性能，为大流量锁止阀设计提供理论指导。

船舶可变螺距螺旋桨，简称调距桨，是20世纪中期发展起来的一种船舶推进装置，目前广泛应用于各种类型的船舶推进系统。采用调距桨的船舶可以在不改变船舶螺旋浆转向和转速的前提下，利用装置遥控操纵系统，使船舶很方便地实现前进、后退、变速、停止等动作，从而大大提高和改善了船舶的机动性和操作性能。

1　锁止阀液压回路分析

在某型船舶调距桨液压系统中，采用锁止阀实现对调距桨的稳距控制，该锁止阀是由两个液控单向阀A、B并联组合而成，如图1所示。

1.泵源　2.溢流阀　3.电液换向阀　4.双向锁止阀 5.液压缸　6.外接负载

调距桨系统工作时，电液换向阀3处左位，主油路进入锁止阀的A1端将阀A开启，油液进入液压缸5无杆腔；同时油液通过控制油路进入到锁止阀B的控制油腔，推动控制活塞将阀B开启，此时液压缸5有杆腔油液通过阀B回油。电液换向阀3中位时，锁止阀4处闭合状态，可保持调距桨桨距。电液换向阀3处右位，锁止阀4反向开启，液压缸5有杆腔进油，无杆腔回油。

2　锁止阀设计模型

在锁止阀的设计中，选用某公司的LC型二通插装阀作为锁止阀的阀芯组件。图2所示为插装阀结构图，图3所示为插装阀原理图。

1.盖板　2.插件　3.阀套　4.调整圈　5.座阀 6.带阻尼的锥颈　7.不带阻尼的锥颈　8.复位弹簧

图3　二通插装阀的原理图

选用该公司A、B、C三种型号的插装阀芯进行模拟测试，分析比较，绘制三种不同型号下的数据曲线，为优化设计提供理论依据。三种型号的插装阀主要技术参数如表1所示。

表1　插装阀主要技术参数

二通插装阀的数学模型可以用以下两个方程进行描述：

阀芯力平衡方程：

p1·A>F+Fv+kx

(1)

式中，p1—— 为进油腔压力

A—— 阀芯接触面积

F—— 为阀芯预紧力

Fv—— 为油液阻力

k—— 弹簧刚度

x—— 弹簧压缩量

阀口流量方程：

(2)

式中：qpv—— 出口流量

AT—— 通流面积

p2—— 出口腔压力

ρ—— 液压油密度

Cd—— 流量系数

3　锁止阀仿真分析

根据设计结构与模型要求，在仿真软件中设定该系统中元件主要参数，见表2。

根据调距桨液压系统原理，建立锁止阀测试系统AMEsim模型如图4所示。

表2　主要参数设置表

1.泵源　2.溢流阀　3.电液换向阀　4.锁止阀 5.液压缸　6.外接负载

3.1　流量对锁止阀特性的影响

对装有三种型号插装阀的锁止阀的特性进行模拟测试。在不同流量下，考察锁止阀单向开启时阀口压差的变化。

现将A、B、C三种型号的插装阀分别放置于锁止阀测试系统中，设置阀口为最大开口量并对其特性进行仿真分析。测试过程中，使系统流量从0 L/min升至600 L/min，读取并计算出每组实验中的锁止阀阀口压差，记录数据并绘制相应的流量-压差曲线(如图5)，进行比较。

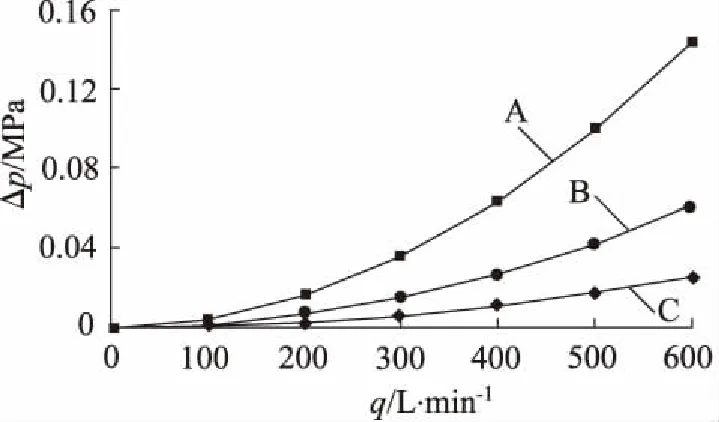
图5　锁止阀单向开启时流量-压差曲线图

某型船舶液压系统工作流量的范围为350～450 L/min， 锁止阀装配A型插装阀时最大压力损失为0.09 MPa，装配C型插装阀时候最大压力损失仅为0.02 MPa。显然选用大通径插装阀阀芯有利于降低锁止阀的压力损失。

3.2　不同阀芯开口量对锁止阀开启特性的影响

对装有A、B、C三种型号插装阀的锁止阀的特性进行设计时，考察不同阀芯开口量对锁止阀开启特性的影响。仿真过程中设定阀芯开口量L为4 mm、8 mm、12 mm以及该型号下阀芯全开的开口量。

在实验中，对每一种型号，每一个开口量进行模拟测试，使系统流量从0 L/min变化至600 L/min，读取并计算出每组测试后的阀口压差，记录数据，根据测试数据绘制相应的流量-压差曲线(如图6～图8)。

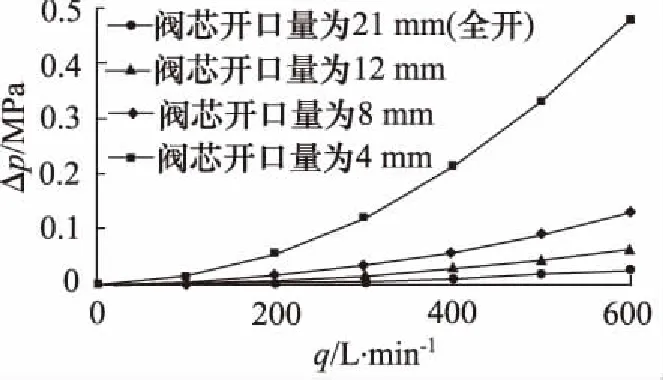
图6　A型插装阀不同开口量下的流量-压差曲线

图7　B型插装阀不同开口量下的流量-压差曲线

图8　C型插装阀不同开口量下的流量-压差曲线

以上流量-压差曲线表明：阀芯的开口量越小，锁止阀正向开启和反向开启的进出口压差变化越是明显，损失越大。当阀芯开口量为12 mm以及阀芯全开时，它们的流量-压差曲线的增长幅度接近，都在0.2 MPa 的范围之内。故在使用该锁止阀时选用阀芯开口量要达到最大值，使得液压油在通过单向阀时压力损失最小。

3.3　控制活塞直径对锁止阀开启特性的影响

控制活塞的有效作用面积AK大于单向阀阀座口的有效作用面积A。因此，为开启通道所需的控制压力小于B口的压力。这两个有效作用面积之比AK/A被称作控制比。当压力pA为0，弹簧预紧力可以忽略不计时，pB与pK之比近似等于控制比。此时控制比也即为开启液控节流通道所需的负载压力与控制压力之比。

反向开启时，由力的平衡方程：

(pK-pA)Ak-FK>(pB-pA)A+

FD+FV+G

(3)

即：

(4)

式中，FD—— 弹簧的预压缩力，N

FK—— 控制活塞的摩擦阻力，N

FV—— 阀芯的摩擦阻力，N

G—— 控制活塞和阀芯的总重量，N

阀芯直径为40 mm时的弹簧预压缩力为444 N, 控制活塞的摩擦阻力和阀芯的摩擦阻力以及活塞和阀芯的总重量之和约为18 N。

在本设计中取控制活塞直径为62 mm，则控制压力pK最小为：

pKmin=pA+0.8(pB-pA)+0.15

(5)

若取直径为50 mm时，控制压力pK最小为：

pKmin=pA+0.64(pB-pA)+0.23

(6)

控制比是锁止阀最重要的一个特性，常见的控制比为1.5～4。当阀芯直径A为40 mm时，考察不同控制活塞直径对阀芯开启时间的影响。

实验中通过改变活塞直径来进行仿真，从而得出测试结果进行分析。活塞直径与其对应的质量如表3所示。

表3　不同活塞直径的控制比和活塞质量

仿真过程中改变模型中控制活塞质量块的质量和控制活塞的直径，逐个进行五组实验，最后将五组控制活塞的位移-时间曲线汇总于图9，通过比较控制活塞的运动速度的变化来分析控制活塞的直径对阀芯开启特性的影响。

图9　不同直径下控制活塞位移变化图

由图9位移-时间曲线可知，控制活塞直径越大，其完全顶开阀芯的时间越短。但整个过程时间最大时间差值约为5 ms，差别甚微。因此，可以认为开启的时间区别很小，故可使活塞的控制比的值在1.5～4的范围内。在这个控制比范围内可以尽量减小控制活塞的尺寸，从而能够减少阀体的几何尺寸和质量。

3.4　双向锁止阀开启过程中液压冲击仿真

选用A、B、C三种型号插装阀，考察三种不同的模型在锁止阀开启过程中液压冲击对系统的影响。在AMESim模型中，在0～1 s中使换向阀处于中位，第1 s 打开换向阀，整个过程运行2 s。仿真后得到锁止阀正向开启图线。设定定量泵的排量为100 mL/r，电动机的转速为4000 r/min。依次绘出A、B、C三种型号插装阀的模型下的阀口压差变化，液压缸移动速度变化，进行比较分析。

图中1～2 s表示锁止阀的开启过程，比较三组图线，图10中显而易见装有B型插装阀的锁止阀的阀口压差的超调约为0.079 MPa，是三组里面最小的。图11中可见B型插装阀在开启过程中，液压油所产生的推力对液压缸的作用变化最不明显。从液压缸的速度这一参数可以反映出该型锁止阀在系统开启过程中系统中力的变化是最微小的，对调距桨系统正常工作的影响最小。

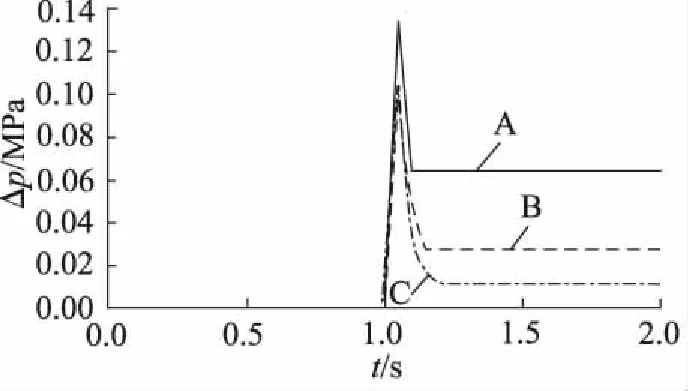
图10　阀口压差变化图

图11　液压缸活塞移动速度变化图

3.5　环流缝隙中液体摩擦对锁止阀开启特性的影响

加工正常的控制活塞与阀体之间有一定间隙，正常工作时期间总有液体。因此在控制活塞和阀体之间总是有液体摩擦：摩擦力与液体黏度、移动速度成正比，与间隙量成反比，力的方向与移动方向相反。可用下列公式表示：

(7)

式中，d—— 控制活塞直径

L—— 控制活塞长度

h—— 活塞与阀体直径的间隙

v—— 控制活塞速度

ρ—— 液体密度

ν—— 液体运动黏度

μ—— 液体绝对黏度

设计中给定活塞与阀座的配合为φ62H7/g6，则其单边间隙h=5～29.5 μm。令:

(8)

则Ff=Kv，此时改变h的大小K即发生变化。K与h的变化关系如表4所示。

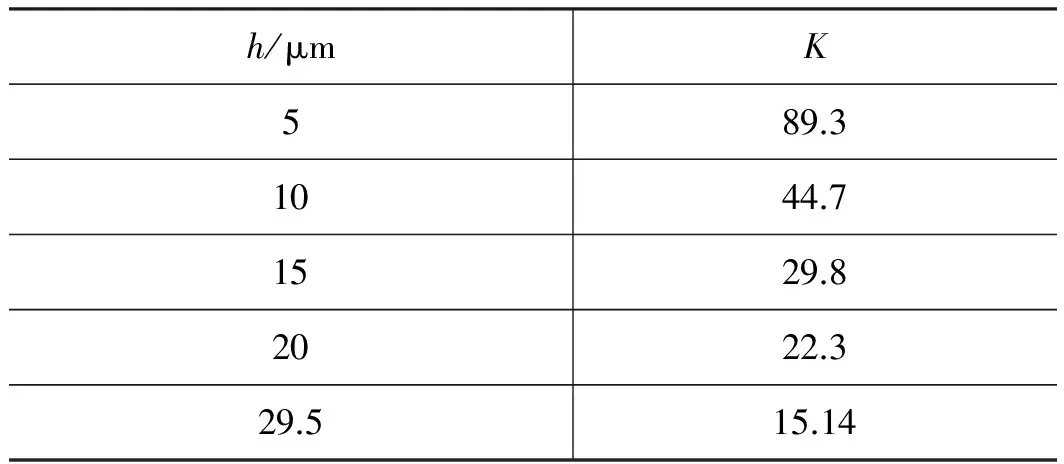
表4　参数K与h的关系对应表

根据活塞处的受力关系可得该处的受力方程为：

p1A-Ff=ma

(9)

其中，p1—— 控制活塞进油腔的压力

A—— 控制活塞的面积

m—— 控制活塞的质量

a—— 控制活塞运动的加速度

变换方程，令:

(10)

从而有:

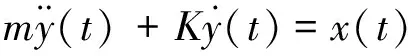
(11)

该系统的传递函数为：

(12)

在MATLAB中对该系统进行仿真，仿真中，代入h=5，h=15，h=29.5三个值，比较其输出的图线。

由图12曲线中得出，活塞与阀体直径的间隙h越大，活塞运动速度越大，开始时间越短。而图13控制活塞开启的摩擦力的三条曲线可知，单边间隙为29.5 μm的模型环流缝隙中液体摩擦力最小，即对控制活塞开启的影响最小。但整个过程均在1 s内完成开启动作，环流缝隙对控制阀开启时间的影响并不明显，但是本设计中，为确保锁止阀反向开启的精确，选用29.5 μm的环流缝隙为宜。

图12　控制活塞开启时的活塞位移-时间曲线

图13　控制活塞开启时的液体摩擦力-时间曲线

4　结论

通过仿真分析可以得出：

(1) 随着系统工作流量的增加，锁止阀压差也随之增大；而采用通径相对较大的插装阀芯，锁止阀进出口的压差相对较小，通过分析比较A、B、C三种型号的插装阀芯得知，C型在系统运行过程中压力损失最小；

(2) 增大阀芯开口量，锁止阀正向开启和反向开启的进出口压差随之减小。建议尽量使得阀芯开口量达到理论上的最大值，使得液压油在通过单向阀时压力损失最小；

(3) 在容许的控制比内，增大控制活塞的直径，阀芯的开启速度变大，但变化幅度较小。若对开启时间要求不高，可适当减小控制活塞直径以减小阀体大小和质量；

(4) 分析比较A、B、C三种型号的插装阀芯在系统开启过程中锥阀阀芯压差的超调量，和锁止阀开启瞬间液压缸速度的变化，可知A型插装阀的锁止阀在系统工作发生液压冲击对锁止阀影响最小，系统运行最为平稳；

(5) 活塞与阀体直径的间隙h越大，活塞运动速度越大，开始时间越短。并且不同的间隙下，活塞所对应的开启时间较为接近，对控制阀开启时间的影响并不明显。

参考文献：

[1]张海平.液压螺纹插装阀[M].北京：机械工业出版社，2012.

[2]雷天觉．液压工程手册[M]．北京:机械工业出版社，2001．

[3]付永领，齐海涛.LMS Imagine.LabAMESim系统建模和仿真实例教程[M].北京:北京航空航天大学，2011.

[4]付永领，祁晓野.AMESim系统建模和仿真一从入门到精通[M]．北京:北京航空航天大学出版社，2006

[5]金小弟，张劲枫，李晶，等.调距桨液压双阀控制系统设计与分析[J].流体传动与控制，2013,(3):8-11.

[6]张晓波，杨璐，徐倩，等.基于AMESim的汽车起重机双向液压锁仿真与优化[J].液压与气动，2011，(4):53-55.