电液步进油缸特性的理论分析及试验研究
, , , (.丽水学院 机械系, 浙江 丽水 000; .中煤科工集团上海研究院, 上海 0000;.IHI(集团)IHI机械系统株式会社, 日本 东京 08-0075)
引言
传统液压系统往往采用各种开关型液压阀来控制液压缸的位移、速度、方向和输出力,但是开关型液压元件难以满足高精度控制场合的需求[1]。虽然伺服技术和比例技术将液压系统的精确控制引入到工业领域,大大推动了工业自动化,尤其是重工业装备的自动化,但是伺服系统构成复杂,成本较高, 抗油液污染能力低, 在对控制精度要求较高且工况条件恶劣的场合容易发生故障,如钢厂连铸设备的结晶器振动控制、调宽控制以及钢水液面高度控制等,一旦失控就会造成机组设备的损坏[2,3]。
为满足高精度和高可靠性要求,日本IHI公司在20世纪70年代将数字控制技术[4],计算机技术和比例伺服技术相融合,开发出内含直接位移反馈可开环控制的电液步进液压缸,并于2012年同中煤科工集团上海研究院合作,面向国内市场研制出新一代电液步进液压缸。本研究采用理论分析和试验相结合的方法,对电液步进缸的静动态特性进行研究。研究表明,该产品性能优良、抗油污能力强,应用前景十分广阔。
1 电液步进油缸工作原理
电液步进油缸的工作原理如图1所示,图中,P、T、LR、LP分别为进油口、回油口、有杆腔泄漏油口和无杆腔泄漏油口。ps为供油压力,pT为回油压力,pc为无杆腔控制压力,Vc为无杆腔控制容积,Ah、Ar分别为无杆腔活塞面积和有杆腔活塞有效面积,Cip为油缸内部泄漏系数,xv、xp分别为阀芯位移和活塞杆位移,mt为活塞和负载总质量,qL为油缸控制腔流量,FL为任意外负载力。
电液步进缸主要由液压缸本体、活塞杆、内置于活塞里的滑阀阀芯、阀套、滚珠丝杆螺母反馈机构、步进电机、编码器以及电器控制单元等组成。其工作原理是:当脉冲发生器产生一个正向指令脉冲信号时,步进电机通过齿轮啮合带动丝杆旋转,并经丝杆螺母副将其自身的旋转运动转为阀芯的轴向位移。阀芯向左运动,阀口开启,压力油进入无杆控制腔,形成差动连接,活塞杆伸出,同时阀套随活塞一起向前运动使阀口关小,构成直接位移负反馈控制,直至阀口完全关闭,活塞杆停止运动。当输入一个反向指令脉冲信号时,步进电机反转,活塞杆缩回。同时,通过编码器实时监测步进电机的运行状况,实现故障预警。
由此可见,活塞杆位移量取决于指令脉冲数,只要连续输入脉冲信号,步进电机就连续旋转,活塞杆便不断伸出或缩回。活塞杆速度由指令脉冲频率决定,输入脉冲频率越高,活塞杆运动速度越快。
2 电液步进油缸的建模与理论分析
根据前节论述分析,可将电液步进缸等效为理想的零开口双边滑阀控制的差动缸系统[5,6],在对其数学模型进行理论推导之前,首先作出以下合理假设:
(1) 液压源为理想恒压源,供油压力ps为常数;
(2) 过流管道和阀腔内的压力损失忽略不计;
(3) 假设液压油不可压缩,密度不变;
(4) 假设阀的节流窗口既匹配又对称,各节流口流量系数相等;
(5) 忽略丝杆圆柱面积对活塞有效面积的影响。
如图1,当丝杠带动阀芯运动,滑阀工作在右位时,油缸控制腔接通压力油,活塞在差动连接作用下伸出。此时,通过滑阀的流量方程:
(1)
式中,Cd为阀口流量系数;W为阀口面积增益;ρ为油液密度。
油缸控制腔的流量连续性方程:
(2)
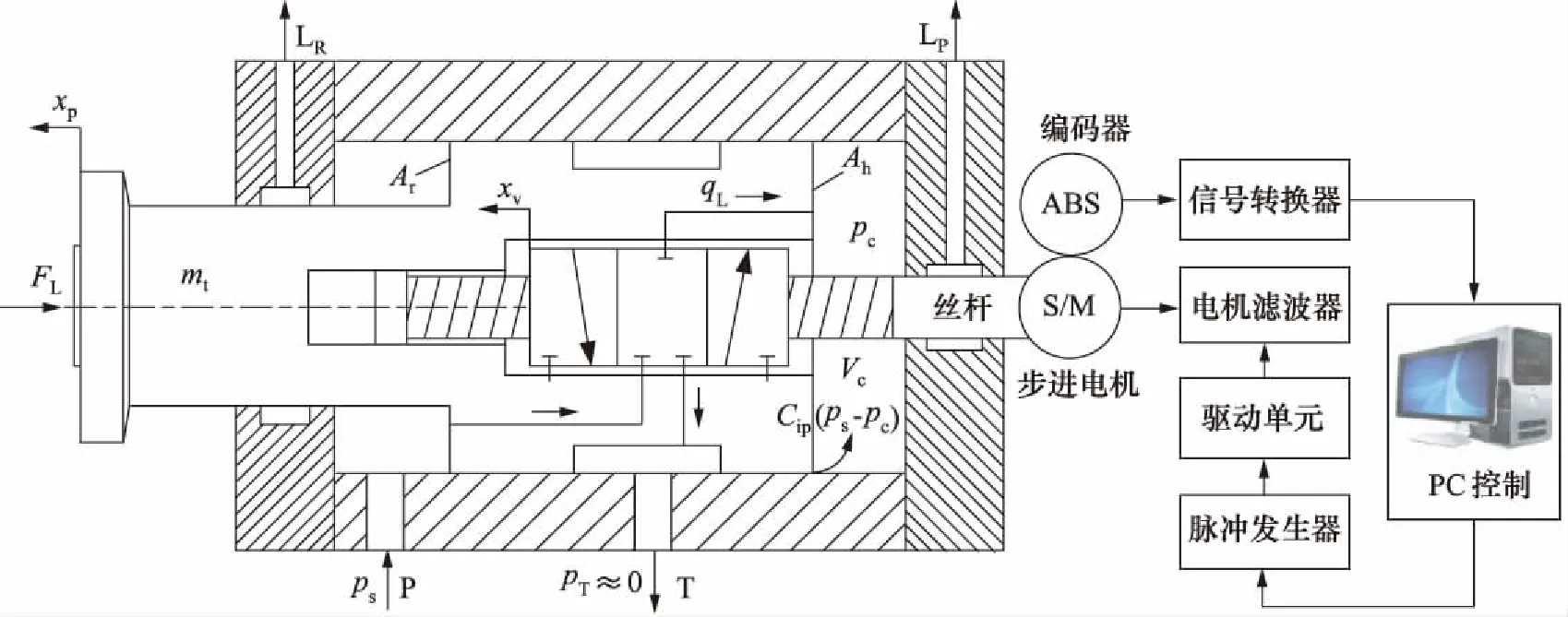
图1 电液步进油缸工作原理图
(3)
式中,V0为油缸控制腔的初始容积;βe为有效体积弹性模量(包括油液、连接管道和缸体的机械柔度)。
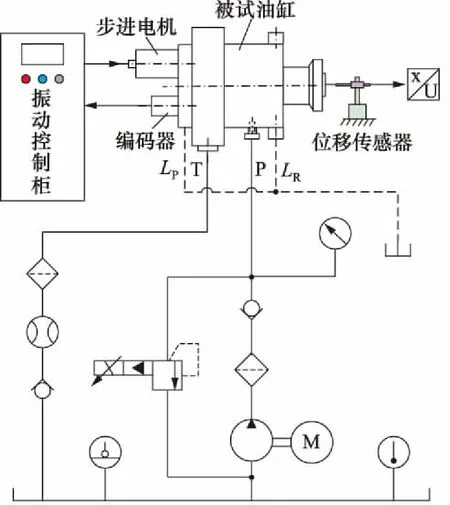
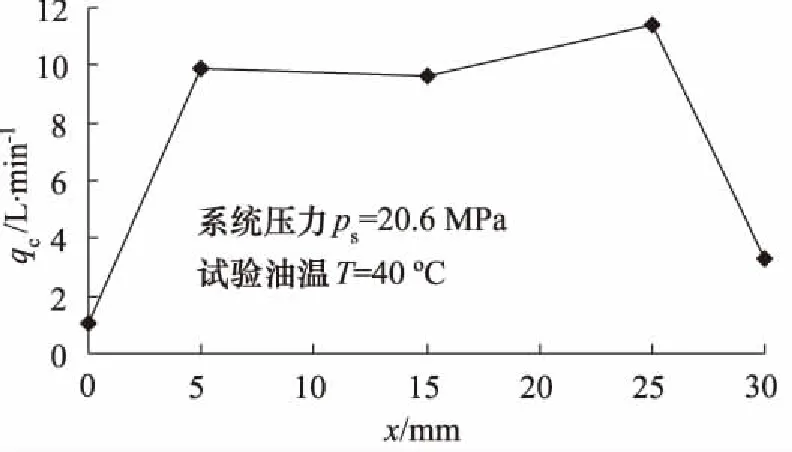
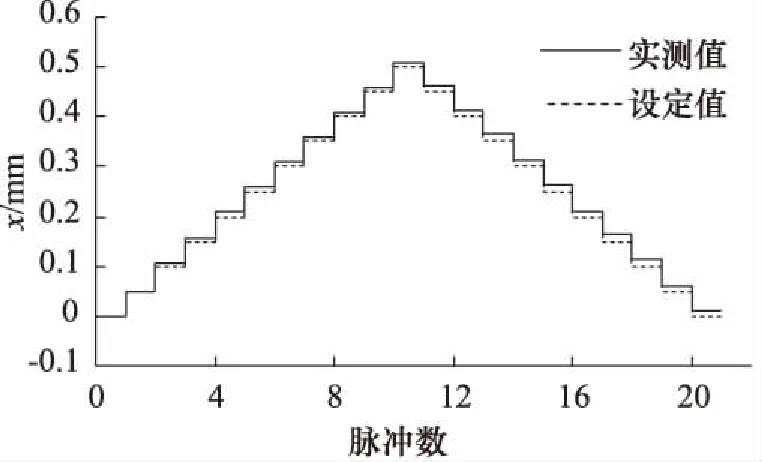
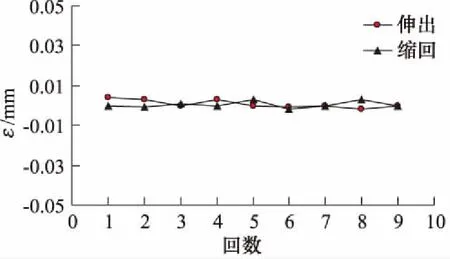
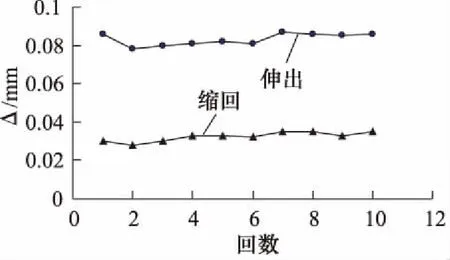
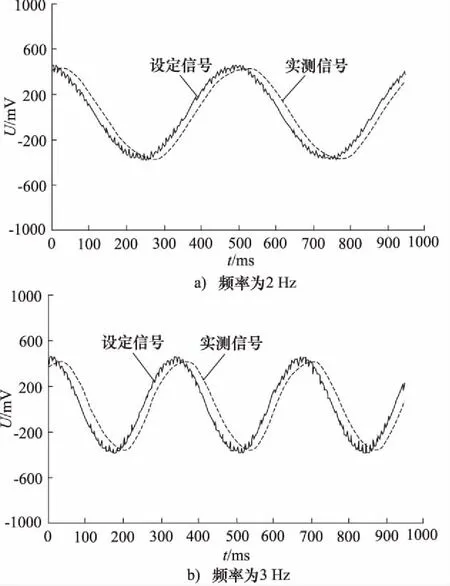
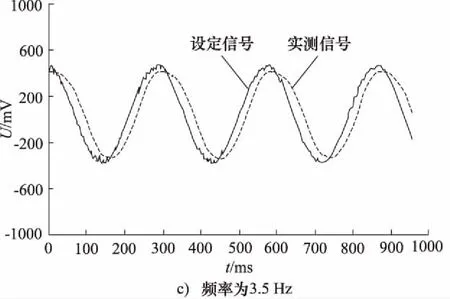
假定活塞位移很小,即|Ahxp|< (4) 活塞和负载的力平衡方程为: (5) 式中,Bp为黏性阻尼系数;K为负载弹簧刚度。 阀芯与滚珠丝杆上的螺母固连,步进电机驱动丝杆做旋转运动,并通过螺母副将其旋转运动转为阀芯的输入位移。当阀口打开后,阀套同油缸活塞一起随动,构成对阀芯的直接位移负反馈控制。因此,阀口开度为: (6) 式中,i为齿轮啮合传动比;θ为步进电机转子角位移;Le为滚珠丝杆的导程。 步进电机的动态特性与转动惯量、阻尼转矩、电磁转矩密切相关[7],可用以下动力学微分方程描述: (7) 式中,J为步进电机转子的等效转动惯量;B为阻尼转矩系数;Tm为转子的最大静转矩;Zr为转子齿数;θi为电机指令角位移;θ-θi为转子的失调角;Zr(θ-θi)为电角度表示的失调角。 若假设电机失调角很小,式(7)可近似为: (8) 对式(1)、式(4)~式(6)、式(8)进行拉普拉斯变换,在零初始条件下得到以下方程: qL=KqXv-Kcpc (9) (10) pcAh=mts2Xp+BpsXp+KXp+FL (11) (12) Js2θ(s)+Bsθ(s)+TmZrθ(s)=TmZrθi(s) (13) 假设不考虑负载刚度和黏性摩擦力的影响,由式(9)、式(10)、式(11)消去中间变量qL和pc可得到电液步进缸活塞的输出位移表达式: (14) 式中,Kce为总流量-压力系数,Kce=Kc+Cip;ωh为液压系统固有频率;ξh为液压阻尼比。 (15) (16) 由式(13)得到步进电机转子角位移表达式为: (17) 式中,ωn为步进电机固有频率;ζ为步进电机阻尼比。 (18) (19) 根据式(12)、式(14)、式(17)可得到电液步进缸系统数学模型方框图,如图2所示。 图2 电液步进缸系统方框图 电液步进油缸的试验原理如图3所示,被试油缸采用日本IHI公司与中煤科工集团上海研究院合作开发设计的ZM/ALMX-3003TC型电液步进缸,油缸行程为30 mm,额定压力为20.6 MPa。步进电机选用5相,2~3相交互励磁方式,步距角为0.36°。驱动器选用斩波调压式电流控制,驱动电源AC110 V±10%(1相),控制电源AC100 V±10%(3相)。电机滤波器为NF-200型,5相/10线,相电阻为0.32 Ω,相电流为8 A。 试验中,通过比例溢流阀调整系统供油压力,通过振动控制柜控制步进电机的脉冲信号并处理编码器反馈信号,采用位移传感器检测油缸活塞杆位移。测量参数有泵的出口压力、油缸的内部泄漏流量以及活塞杆位移。步进电机指令信号与采集的位移信号在计算机内通过专用数据处理软件进行处理。 图3 试验原理图 设定系统压力为20.6 MPa,空载状态,油缸活塞分别处于行程内任一点及两终端位置时,可测得油缸在各位置时的内泄漏流量,如图4所示。可见,油缸最大内泄漏量不超过12 L/min。若不考虑阀口泄漏与油液压缩性的影响,稳态时,油缸内泄漏量只与有杆腔和无杆腔的压差(ps-pc)有关。在行程两终端位置时,活塞杆顶死,无杆腔控制压力升高至供油压力,两腔压差基本为零,内漏量最小。在行程中时,由于Ah>Ar,当活塞杆达到静力平衡时,ps-pc=(1-Ar/Ah)ps,即两腔压差为一定值,内漏量较大。 设定系统压力为20.6 MPa,测定行程为0.5 mm,油缸活塞以1 PPS的速度空载往复运动1次,到测量起始点位置的行程脉冲量为10个脉冲。在行程的中间位置,可测得输入1个脉冲时的活塞动作,用变位仪记录在波形解析记录仪上,得到10脉冲行程测试曲线如图5所示。将图中前进侧的油缸行程(0.508 mm)与输入10脉冲变位量(0.5 mm)之差作为10脉冲精度。 图4 内泄漏流量试验曲线 图5 10脉冲行程测试曲线 在10脉冲行程测试曲线上,分别读取每一步油缸伸出和缩回时位移量,并与输入的1脉冲变位量(0.05 mm)之差作为一步精度。试验测得的一步精度曲线如图6所示。由曲线可知,被试油缸在一个往复测量行程内,一步精度最大偏差值为0.004 mm,最小偏差值为-0.002 mm,均在判定基准±0.05 mm以内。 图6 一步精度试验曲线 在系统压力20.6 MPa,行程中间位置上测定行程20 mm,油缸活塞以输入速度1900 PPS,基速(自起动)500 PPS,加减速时间常数30 ms,空载往返运动10次。用变位仪测量活塞伸出和缩回时的停机位置重复偏差,并记录在波形解析记录仪上,得到的重复位置偏差曲线如图7所示。取图中位置偏差最大值与最小值之差作为重复位置精度,可见,油缸伸出时重复位置精度为0.009 mm,缩回时为0.007 mm。 图7 重复位置偏差试验曲线 步进油缸的动态特性一般用对正弦激励和非正弦激励信号的频率响应来衡量。图8为试验得到的步进缸对正弦波信号的跟踪曲线。图8a为频率2 Hz;图8b为频率3 Hz;图8c为频率3.5 Hz。图中,横坐标表示时间,纵坐标表示设定信号电压及活塞位移信号转换的电压值。试验中,油缸活塞位移振幅为2 mm,由于存在噪声干扰,设定信号曲线光滑度较差,须进一步降噪处理。 图8 频率响应试验曲线 由图可知,在振动频率不超过3 Hz时,被试油缸的对正弦信号的跟踪能力较好,输出波形无明显失真,跟踪精度较高。但当振动频率高于3 Hz,如达到3.5 Hz 时,输出波形明显发生畸变,波形峰值达不到给定值,油缸跟踪能力较差。说明在一定频域范围内,频率越低,电液步进缸对正弦信号的跟踪能力越强。 (1) 电液步进缸利用内置式伺服阀直接位移反馈原理,无需电子传感器及相应的检测电路,可直接开环控制,具有出力大、控制精度高、动态响应快、抗油污能力强(能适应NAS11级液压油)、结构简单紧凑、可靠性高等优点。可广泛应用于钢厂的高炉、连铸机及其它处于恶劣工况的高精度工业设备中; (2) 电液步进缸采用增量式数字控制方式由步进电机驱动。数字信号在恶劣环境下不易衰减,抗干扰能力强,便于利用计算机系统实现远程网络控制; (3) 电液步进缸的位移与指令脉冲数成正比,运动速度与指令脉冲频率成正比。只要提供的指令脉冲数相同,就可同步高精度地控制多个油缸; (4) 在活塞杆上增设位移传感器可构成电闭环控制,用以补偿系统温度、外负载力、油液压缩性、内泄漏及伺服阀死区等因素的干扰,可进一步提高电液步进缸的控制精度。 参考文献: [1]孙峰,马群力.数字式液压缸和数字式液压系统[J].液压与气动,2002,(8):42-44. [2]李运华,陈栋梁.基于电液伺服控制实现的连铸机结晶器振动装置[J].机械工程学报,1999,35(1):72-75. [3]郜立焕,史小波,李建仁,等.闭环控制电液步进液压缸及试验精度分析[J].机床与液压,2010,38(11):67-68. [4]肖志权,彭利坤,邢继峰,等.字伺服步进液压缸的建模分析[J].中国机械工程,2007,18(16):1935-1938. [5]曹钧凯.内置伺服阀式电液步进缸的改进设计与仿真[D].沈阳:东北大学,2012. [6]李洪人,王栋梁.非对称缸电液伺服系统的静态特性分析[J].机械工程学报,2003,39(2):18-22. [7]史敬灼.步进电动机伺服控制技术[M].北京:科学出版社,2006.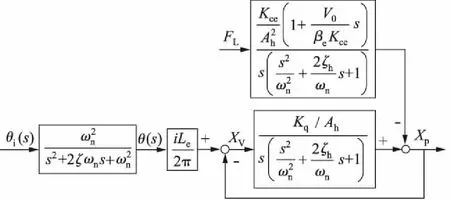
3 电液步进油缸的试验测试
3.1 研究方法和试验原理
3.2 静态特性
3.3 动态特性
4 结论

