基于IQGA和SR的微弱信号检测方法研究

，

(军械工程学院 导弹工程系， 河北 石家庄 050003)

引言

随机共振(Stochastic Resonance, SR)自1981年由意大利学者Benzi. R提出以来，经过30多年的发展，已成为检测微弱信号的研究热点之一。与其他去噪方法不同，随机共振充分利用噪声，将其部分能量转化为信号能量，从而实现降噪的目的。自适应随机共振的出现是随机共振发展的一个里程碑，它不需要信号和噪声的先验知识，通过调整系统参数，便可以使系统达到随机共振，从而对微弱信号进行检测。

在以往的自适应随机共振研究中，常采用遗传算法(Genetic Algorithm,GA)[1]、粒子群算法[2]等对自适应随机共振的参数进行优化，从而使系统达到最佳共振的状态。但在优化的过程中，若选择、交叉和变异的方式不当，遗传算法常会出现迭代次数多，收敛速度慢、易陷入局部极值等现象。量子遗传算法(Quantum Genentic Algorithm, QGA)是基于量子计算原理的一种遗传算法，避免了遗传算法的一些缺陷，实现了比常规遗传算法更好的效果，目前已广泛应用于各个领域。量子遗传算法将量子的态矢量表达引入遗传编码，利用量子逻辑门实现染色体的演化，但QGA的编码方案和量子旋转门的演化策略通常不具备通用性，特别是在所有的个体均向同一个目标演化的情况下，没有交叉操作的QGA极易陷入局部最优[3]。

本研究针对上述情况提出了一种改进的量子遗传算法(Improved Quantum Genetic Algorithm, IQGA),在量子门更新的过程中适当的改变旋转角，并加入了量子的交叉和变异操作。并将改进的QGA应用于随机共振，从而实现对微弱信号的检测。

1 改进的量子遗传算法

1.1 量子遗传算法

量子遗传算法是一种将量子计算原理和遗传算法相结合的随机搜索优化算法。QGA与GA相比，保持了较好的种群多样性，且具有良好的全局搜索能力。

量子遗传算法的核心是量子比特编码和量子门更新。在量子计算中，量子位是信息的载体，一个量子位的状态可表示为：

|φ|=α|0|+β|1|

(1)

式中， |0|,|1|分别表示自旋向下和自旋向上；(α,β)表示相应状态出现概率幅的两个复常数，满足下列归一化条件：

|α|2+|β|2=1

(2)

式中，|α|2,|β|2分别表示|0|,|1|的概率。

根据不同问题的特点，可以设计不同的进化过程执行机构，即量子门。一般情况下，常选用量子旋转门，其更新过程如下：

(3)

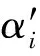
1.2 改进的量子遗传算法

量子遗传算法在量子门的更新过程中常选用固定的旋转角策略。旋转角过小，不利于迅速找到最优个体，影响寻优速度，旋转角过大则影响最优个体适应度值的精度。因此，旋转角应随着进化代数的增加而减小[4]。由于旋转角的取值范围通常为[0.001 π,0.05 π][5]，那么假设在进化的第一代，使旋转角为最大值0.05 π，随着进化代数的增加，旋转角非线性减小，到最后一代时，使旋转角达到最小值0.001 π，那么旋转角可进行如下改进：

(4)

其中，θmin,θmax分别为旋转角取值范围的最小值与最大值，gen为当前进化代数，genmax为最大进化代数。

与此同时，在量子门的更新过程中加入量子交叉和变异的操作。在量子遗传算法中，进化目标是个体当前最优确定解和其对应的适应度值，这也最能体现个体的结构信息，若将二者进行互换，实现量子的交叉操作，进化过程将受到其他个体的影响，从而获得新的进化信息。量子交叉操作的基本步骤是在进化的过程中，在个体之间暂时的交换当前最优确定解和其对应的适应度值，接受交叉操作的个体的进化方向将受到其他个体的影响，从而得到新的进化信息。量子变异则是通过轻微的打乱某个个体当前的进化方向，以防止该进化过程陷入局部最优。量子变异操作的基本步骤是利用单点变异和多点变异相结合的方式，互换染色体编码中量子比特概率幅(α,β)的值，彻底反转个体的进化方向，从而增强种群的多样性，有效的避免算法陷入局部最优。

1.3 标准测试函数

采用Schafferl函数验证本研究提出的改进的量子遗传算法的有效性。

Schafferl函数的表达式如式(5)所示：

minf(x,y)=(x2+y2)0.25×[sin2(50×

(x2+y2)0.1)+0.1]-10≤x,y≤10

(5)

该函数只有一个极小值点，极值点为(x,y)=(1,1)， 极小值为fmin=0，其三维函数图像如图1所示。

采用文献[6]提出的改进的遗传算法、量子遗传算法和文献[7]中提出的改进的量子遗传算法对标准测试函数Schafferl函数进行求解，并与本研究方法进行寻优效果的对比。各算法的参数如下：四种方法的种群大小均为100，个体长度均为20，最大进化代数均为350；IQGA的交叉概率为0.7，变异概率为0.05。分别计算10次求平均结果。对比结果如表1和图2所示：

从表1和图2可以看出，提出的IQGA的最优寻优结果比其他方法高出3个数量级以上，且收敛代数也大幅度的降低，说明其收敛速度快，效率高。

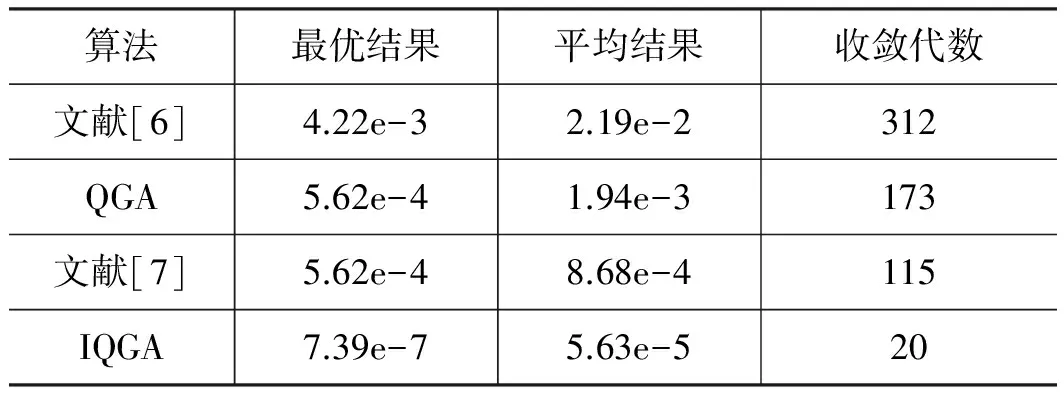
表1 算法性能比较

图2 各算法进化过程图

2 基于IQGA的随机共振

2.1 随机共振简介

在噪声与周期信号的共同作用下，可引起随机共振现象的发生。这种作用下的双稳系统可由朗之万方程(Langevin Equation, LE)表示如下：

(6)

其中，均a,b为大于零的实数，驱动信号Acos(2πf0t)的振幅为A，频率为f0,ζ(t)是强度为D均值为零的高斯白噪声，且有：

<ζ(t),ζ(0)>=2Dδ(t)

(7)

信噪比是衡量随机共振的指标之一，本研究利用信号的功率求系统的输出信噪比：

SNRout=10lg(psignal/pnoise)

(8)

其中，psignal=|Y(k0)|2是信号的估计功率谱，Y(k)是输出信号的傅里叶变换：

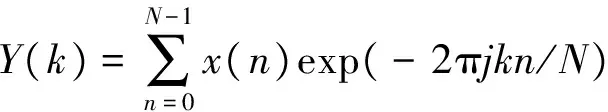
(9)

式中，N为数据长度，且：

n=0,1,…,N-1，k=0,1,…,N-1

在小噪声强度下，|Y(k)|2得到的最大值在k0处。白噪声的功率谱是常数，在信号中估计噪声功率谱可以用下述方法：

其中，M=5，为接近信号频率噪声的带宽。

2.2 IQGA与随机共振

令经随机共振系统处理后信号的输出信噪比为个体的适应度函数，对系统参数a和b进行同时优化，根据式(6)、(8)、(10)和四阶龙格-库塔方程，可得目标函数SNRout的表达式为：

(11)

式中，Sn代表驱动信号和噪声信号共同构成的输入信号，x代表随机共振系统的输出信号，|X(z0)|2代表输出信号的估计功率谱，h为四阶龙格-库塔方程的步长，取h=1/fs。

基于量子遗传算法的自适应随机共振算法流程图如图3所示,其具体过程如下：

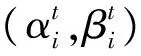
(2) 将各个参数输入二阶欠阻尼随机共振系统，利用四阶龙格库塔解方程，并得到系统的输出信噪比；

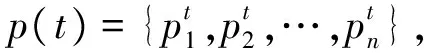
(4) 将输出信噪比作为目标函数，对p(t)中的每个个体进行评价，并记录最优个体和对应的适应度；

(5) 判断优化过程是否可以结束，满足条件则退出，否则继续计算；

(6) 重复步骤(2)～(4)，利用量子旋转门对个体实施调整，得到新的种群；将Q(t+1)迭代次数t加1，返回步骤(5)。

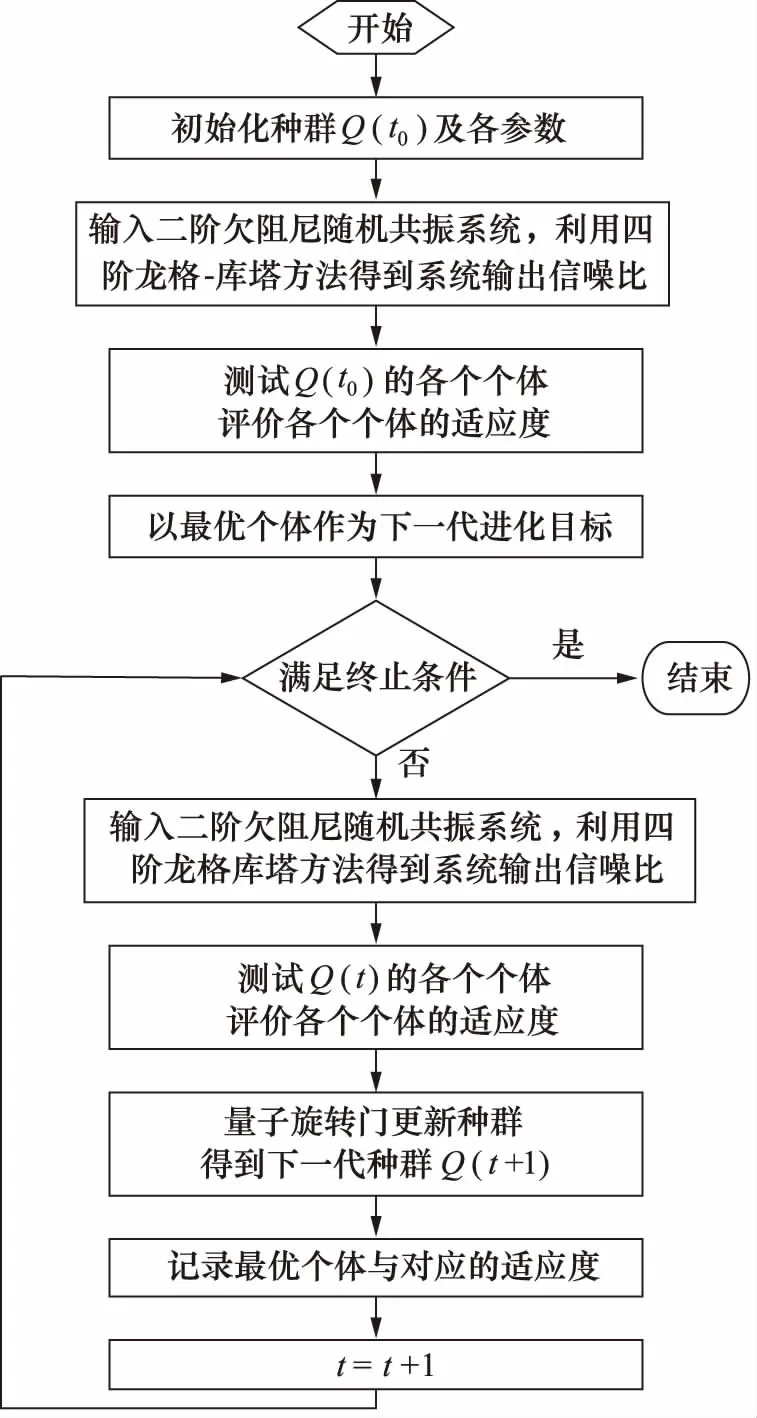
图3 基于量子遗传算法的自适应随机共振流程图

3 仿真信号分析

设信号的采样频率为5 Hz，采样时间为500 s，采样点数为2500点；驱动信号Acos(2πf0t)的振幅A为0.03，频率f0为0.05 Hz,ζ(t)的强度D为0.5，则信号的输入信噪比为-23.0103 dB。利用四阶龙格-库塔进行求解，步长h为0.02；为了保证随机共振求解过程中的收敛性，参数a和步长h应遵循以下关系[8]：a×h≤1。确定系统参数a和b的取值范围分别为[0.01 5]和[0.01 10]。

设GA,QGA和IQGA的最大进化代数为300，种群大小为100，GA的代沟、交叉概率及变异概率分别为0.95、0.7、0.05。运用上述三种方法分别对随机共振系统的参数a和b进行优化，优化结果及进化过程分别如表2、图4所示。

由表2可知，本研究提出的优化算法可以得到最大信噪比。从图4可以看出，QGA在第20代时可能陷入局部最优；IQGA经过交叉和变异的操作，避免了这种情况。虽然IQGA的最优解终止代数与GA相近，但优化结果较GA而言更为理想。将各算法优化后参数代入随机共振，得到的信号时域图和频谱图分别如图5、图6所示。

表2 各算法优化结果

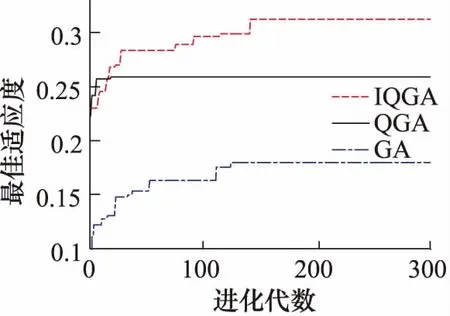
图4 各算法进化过程图

图5 信号的时域图

图5所示的分别是系统含噪信号的时域图和经不同算法优化后的参入代入随机共振处理后的时域图。在信号未经过处理时，信号被湮没在噪声中，无法分辨；而经过GA优化参数的随机共振处理后的信号失真较大；经过IQGA优化参数的随机共振处理后的信号含噪成分最少。

图6是图5对应的频谱图。含噪信号的频谱图不能分辨信号的频率。参数经过算法优化后的随机共振处理的信号频谱图可以清晰的将频率0.05 Hz分辨出来。但经GA优化参数的随机共振处理后输出的信号频谱谱值较低，经QGA优化参数的随机共振处理后输出的信号频谱谱值虽有提高，但是2倍频、3倍频处谱峰较为明显，影响工程上对故障的判断。经IQGA优化参数的随机共振处理后的输出信号频谱最为清晰，振幅最高，效果最好。

图6 信号的频谱图

4 工程应用

斜盘式轴向柱塞泵包含的多对摩擦副中，滑靴与斜盘之间的摩擦副最为复杂[9],故斜盘磨损是液压泵最容易发生的故障之一，其振动信号获取方便且包含有丰富的故障信息。本研究采用试验器件名称及型号如表3所示。

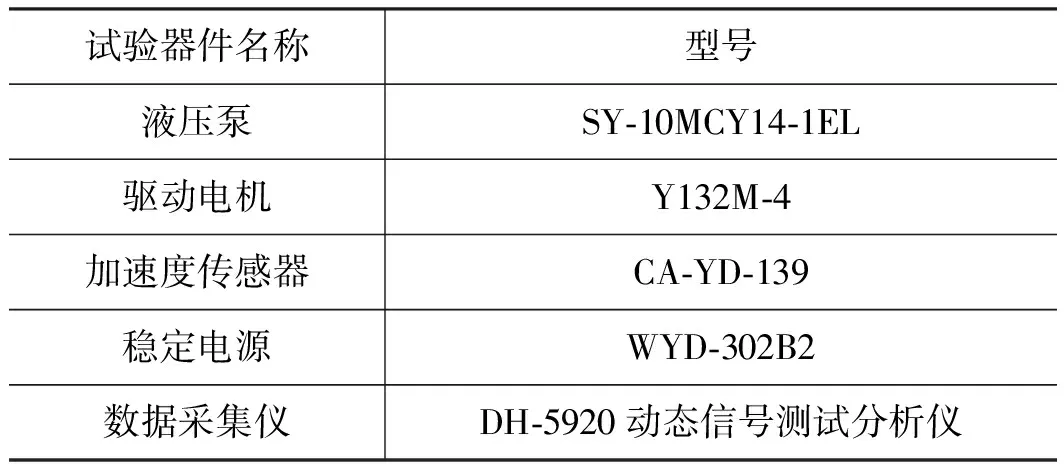
表3 试验器件名称及型号

其中，驱动电机的额定转速为1480 r/min；液压泵的柱塞数为7，理论排量为10 mL/r，额定转速为1500 r/min，液压泵主溢流阀压力为10 MPa，采样频率为20 kHz，采样点数为5000。由于泵轴的转速为1500 r/min,单个柱塞附加冲击的基频为f=n/60 (n为电机的转速)，则本试验的液压泵的冲击振动基频为7*f=175 Hz。替换正常部件的故障部件如图7所示。

图7 斜盘磨损故障件

采集信号的时域图和频域图如图8所示。

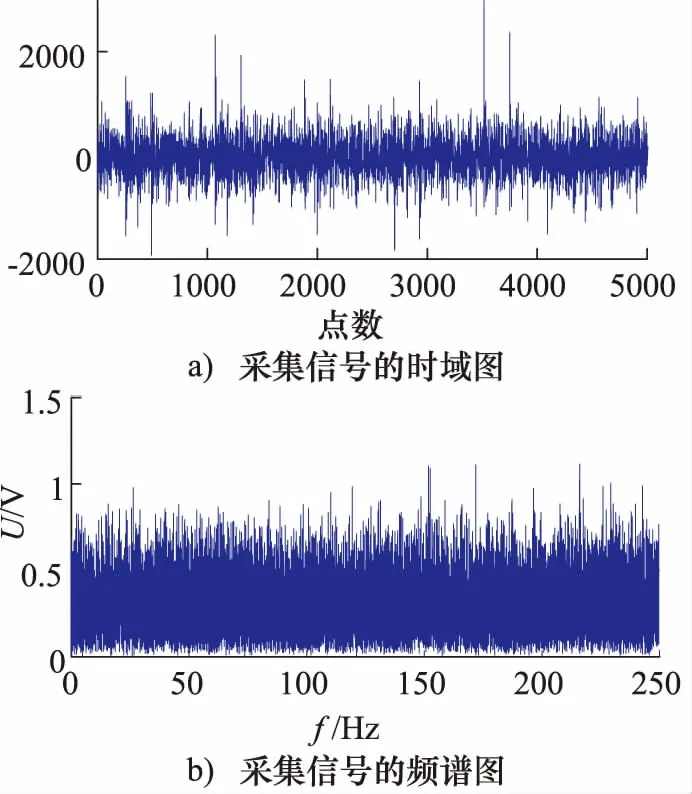
图8 采集信号

传统随机共振因遵守绝热近似理论，故只能检测频率远小于1 Hz的信号，但实际试验中，如本试验所检测的频率为175 Hz，远大于1，故采用变尺度随机共振方法[10]先对采集到的信号进行线性压缩，再利用本研究提出的IQGA对随机共振系统参数进行优化，并对信号进行处理，最后按压缩尺度还原实测数据。设置压缩倍数为250，系统参数a,b及IQGA的参数取值范围与仿真信号相同。计算得出，经过72次迭代，算法收敛，参数的a,b的最优值分别为，a=1.032，b=4.936，其处理后的信号时域图和频谱图如图9所示。

经处理后的信号在时域内周期性明显，在频域内，检测到的频率为172 Hz，与液压泵的冲击振动基频175 Hz相近。因此，提出的方法可以在工程上得到较好的应用。

5 结论

提出了一种改进的量子遗传算法，通过调整旋转角的大小，使整个进化过程在初期时可以迅速寻优，在后期时保证最优个体适应度值的精度；并在量子门更新的过程中加入了交叉和变异的操作，防止其陷入局部最优， 保证了算法良好的全局搜索能力和种群的多样性。将改进的方法与随机共振相结合，将信噪比作为个体适应度目标函数，对随机共振的参数进行优化，从而实现了强噪声背景中微弱信号的提取。工程实践证明，改进的方法可取得较好的效果。

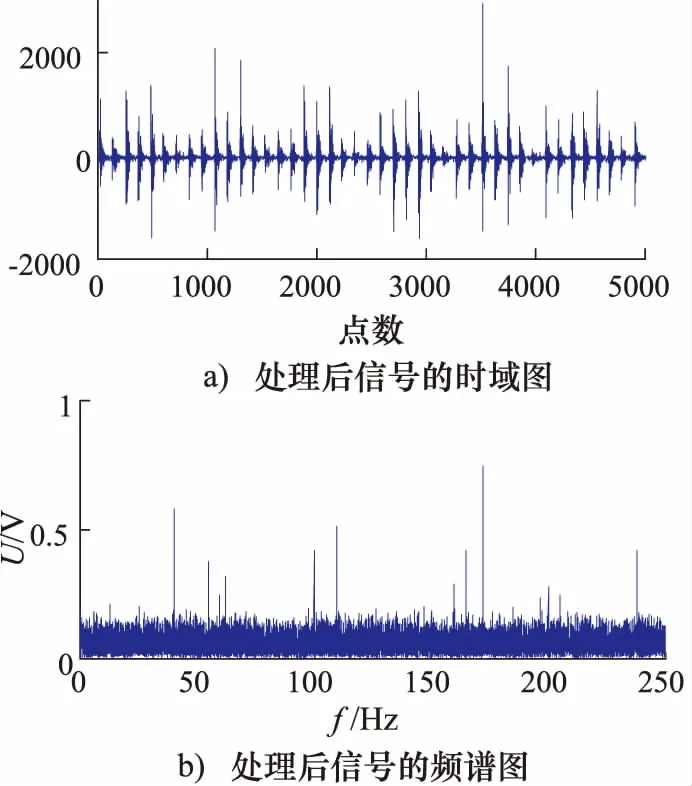
图9 经QGA和二阶欠阻尼SR处理后的信号

参考文献：

[1] 王晶，张庆，梁霖，等.采用遗传算法的自适应随机共振系统弱信号检测方法研究[J].西安交通大学学报,2010,44(3):32-36.

[2] 李继猛，陈雪峰，何正嘉.采用粒子群算法的冲击信号自适应单稳态随机共振检测方法[J].机械工程学报,2011,47(21):58-63.

[3] 杨俊安，庄镇泉.量子遗传算法研究现状[J].计算机科学,2003,(11)：13-15,43.

[4] 曾成，赵锡均.改进量子遗传算法在PID参数整定中的应用[J].电力自动化设备,2009,29(10):125-127,139.

[5] Han K H, Kim J H. On Setting the Parameters of Quantum-inspired Evolutionary Algorithm for Practical Applications[C]. Canberra, Australia: Proc Congr Evolutionary Computation,2003:178-184.

[6] 郭佳凡，于吉全.基于遗传算法的大型钢塔结构的节点损伤参数识别方法[J].湖北大学学报(自然科学版),2009,31(4):379-383.

[7] 张瑞刚.基于模态分析的发射台机械结构损伤识别方法研究[D].石家庄：军械工程学院,2012.

[8] 谢磊.轴承振动分析与寿命评估方法研究[D].成都：电子科技大学，2013.

[9] 张长英，龚晓群，李萍萍，等.斜盘式轴向柱塞泵的减摩降噪措施[J].液压与气动，2013,(12):118-120.

[10] 范胜波，王太勇，冷永刚，等.基于变尺度随机共振的弱周期性冲击信号的检测[J].中国机械工程，2006,17(4)：387-390.