民用飞机液压能源系统可靠性分析

， ， ， ， 俊晖，

(1.中航机电系统有限公司， 北京 100028； 2.浙江大学 机械工程学院， 浙江 杭州 310000；3. 航空机电系统综合航空科技重点实验室， 江苏 南京 211100)

引言

民机液压系统是多余度、大功率的复杂综合系统，由多套相互独立、相互备份的液压系统组成。为保证飞行安全可靠，现代民机(如A320、B737)液压系统普遍采用余度设计，即由两套及以上相互独立的液压系统互为备份。但是对于具体的能源配置方案，其可靠性到底能达到何种程度，整套液压系统的无故障时间大概有多长，国内对此还没有进行充分的研究。本研究以某型民机液压系统为依托，根据飞机飞行控制要求，针对飞机液压能源系统体系结构及组成，提出了民用飞机的液压系统可靠性分析方法，通过分析获得飞机液压能源系统可靠性数据以及重要度，并对比分析了不同民机液压系统的可靠度。

1 基于威布尔分布的液压元部件失效率分析方法

一般将失效率当作已知量来分析液压系统的可靠度时，并不会考虑液压系统的失效概率密度分布，即当作常量进行计算。但是，如果需要对航空液压系统进行分析，则需要在原来的基础上，考虑适用于航空液压系统的概率分布。航空系统的失效概率密度更适用于使用威布尔参数进行分析[1]，因为无论泊松分布或者指数分布，都可认为是威布尔分布的特例。

1.1 威布尔分布方法

威布尔分布也称为韦伯分布，由1951年瑞典数学家Waloddi Weibull提出[2]，是一种更加适用于飞机液压能源系统的概率密度分布方法。它使用只有2～3个样本时仍有非常好的效果，且其所有可靠性基本函数均有封闭的解析表达式，尤其是在经过双对数变换后能可线性化[3]，其概率密度分布函数为连续函数。本研究采用二参数威布尔分布方法，可大大减少计算量，其概率密度函数为：

(1)

其中，t为时间随机变量；β为比例参数；k为形状参数。

当k=1，威布尔分布可以变为指数分布，因此威布尔分布函数可以有效涵盖可靠性分析需用到的连续函数。这里我们需要分析并求得的参数应该是：β、k，进而得出概率密度和系统对应的可靠度，然后求出失效率，最后求得平均失效时间[4]。

由二参数威布尔分布的数值计算方法[5]，威布尔分布可以转化为线性关系。

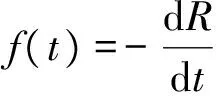
(2)

以上式子可以看到属于Y=AX+B的直线公式，即可以运用最小二乘法进行分析求解。当实际数据比较少时，因为可靠度指的是概率事件，因此可以使用平均秩方法计算可靠度，即公式如下：

(3)

其中，也可以选择使用[7]：

(4)

本研究选择使用第一种方法，得到数据分析方法如图1所示。

图1 设计分析流程

1.2 飞机液压能源系统元部件失效率分析方法

航空液压系统与一般液压系统可靠性分析的不同主要表现为：元部件失效率、安全冗余度，失效概率密度函数。航空液压系统的失效概率密度函数更倾向于威布尔分布。假设分析其中一个元部件EMP，即电动机驱动泵的失效概率密度。首先需要知道其试验数据，由于我国的民用飞机研究较迟，该数据暂时还无法获得。引用前人论文中的数据如表1[8]。

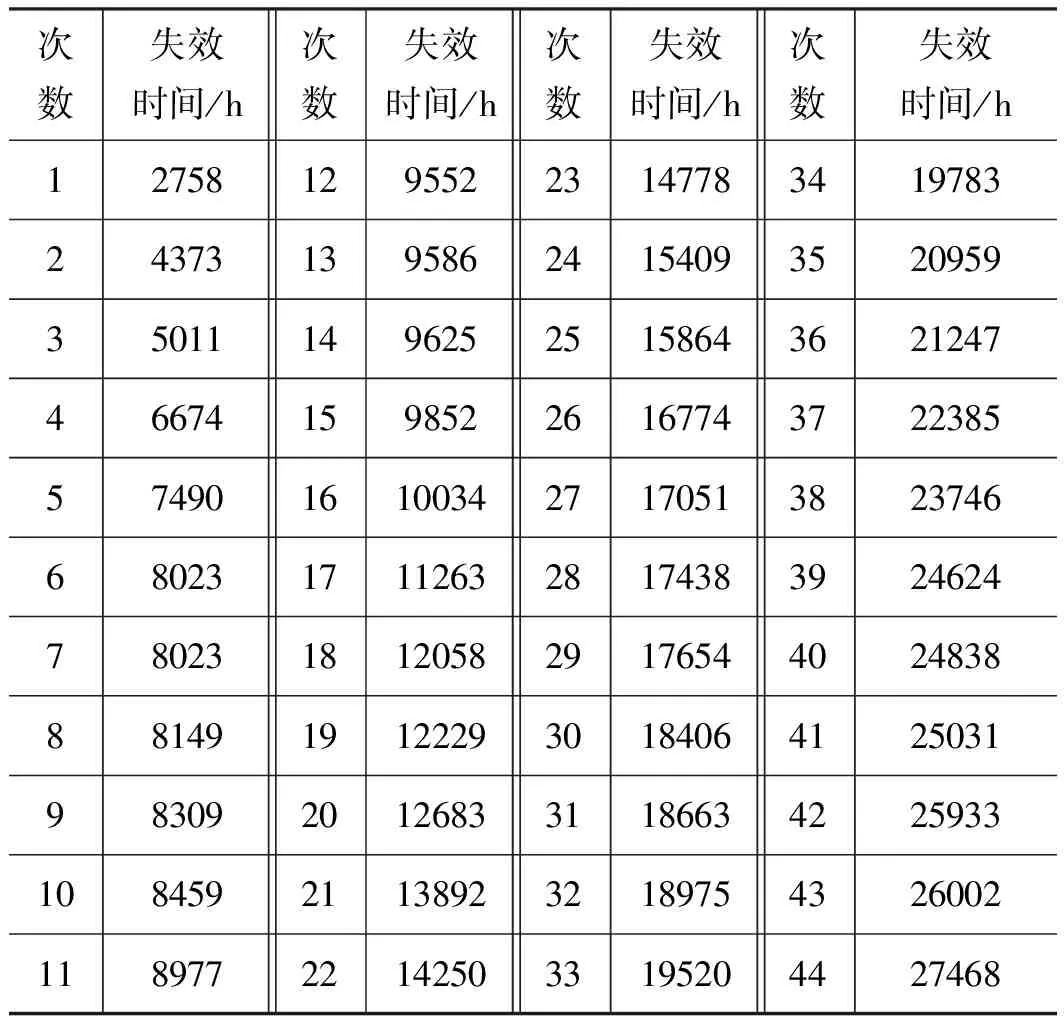
表1 某型民用飞机EMP测试参数

(1) 首先，将参数进行归一化，即将已经知道的参数进行平均秩转换，得到对应的可靠度概率：

(5)

(2) 将R进行双对数取值，由于使用二参数方法进行分析，因此在不考虑该数据平移的情况下，将参数进行线性化，转化为线性公式：

(6)

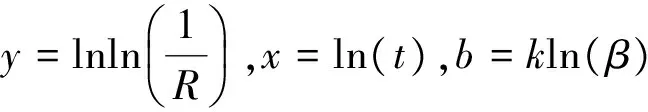
y=kx-b

(7)

(3) 代入数据， 得到：k=2.1607，b=21.0841，β=17292。

可以获得最后的试验参数：

(8)

(9)

(10)

(4) 使用二参数法进行数据分析，还需要检验二参数法是否正确。最常使用的方法是利用相关系数[9]，通过计算相关系数可以获得随机变量之间的概率统计规律[10]。按照可靠性定义分析，对最小二乘法的转换参数进行相关系数计算：

(11)

假设飞行时间10 h，可以得出相关系数为0.992，相关系数十分接近1，说明使用二参数是正确的方法。

由式(10)求得EMP的失效率表达式如公式(12)所示：

(12)

2 某型民机液压系统可靠性分析

2.1 液压系统能源配置方案

本研究提出的民机液压系统，采用三套互相独立的液压系统。1#系统使用一个EDP和一个EMP，2#系统使用一个EDP，3#系统使用两个EMP，其中1#系统的EDP、2#系统的EDP以及3#系统的EMP作为主系统工作，其余作为备用系统。1#和2#系统间设置有双向能源转换装置PTU，对2#系统进行能量控制。液压系统功能框图如2所示。

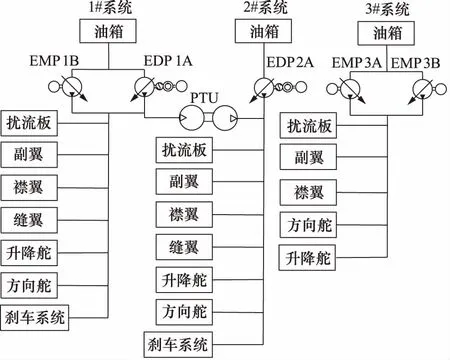
图2 某型民用飞机功能图

2.2 液压系统元部件失效率

参考某型飞机液压能源系统中各元部件的失效率数据，获得系统各元部件的工作时间。采用1.2中提出的元部件失效率分析方法，我们可以获得失效率参数，如表2所示。在后续的计算中，失效率数据均以下表中的数据为准。

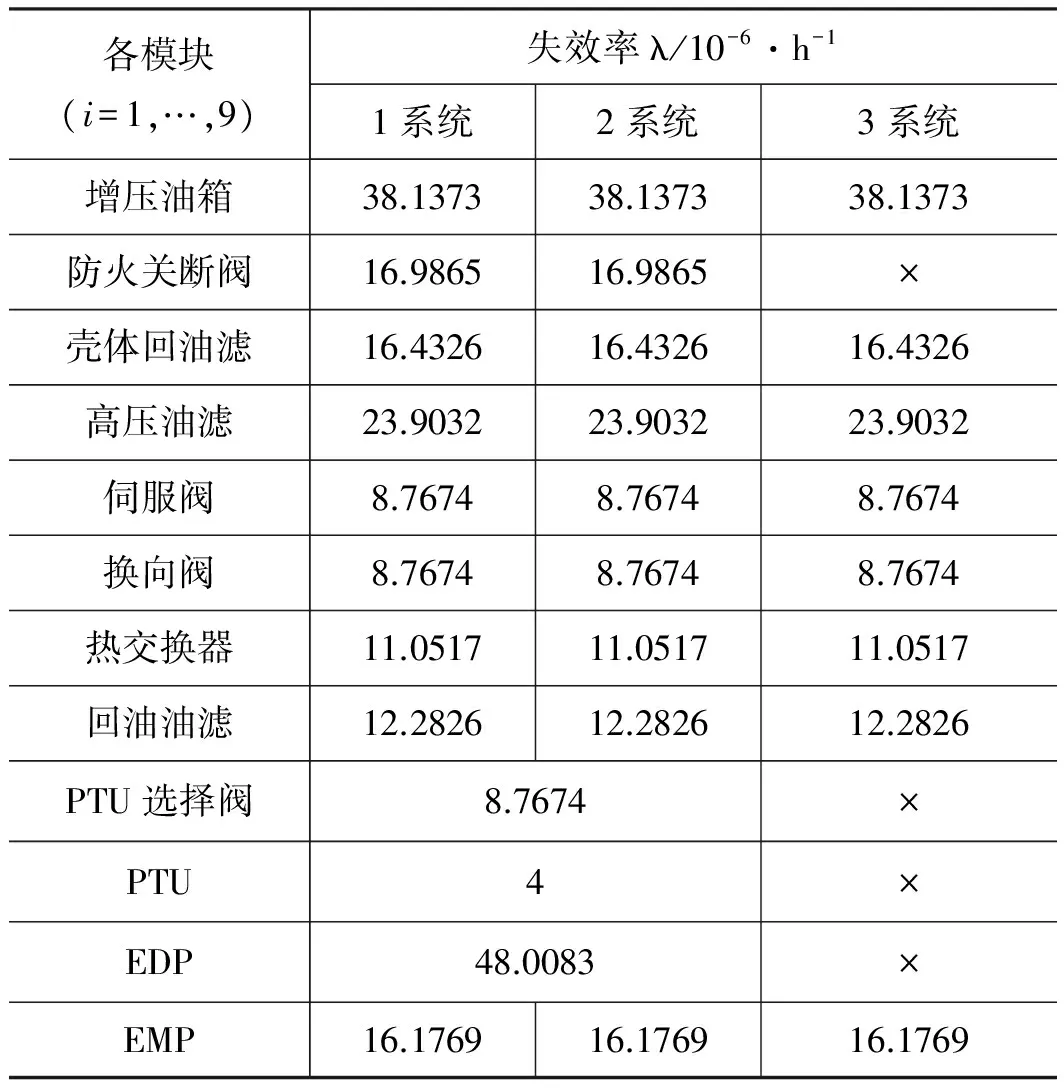
表2 各元部件失效率参考数据

2.3 民机液压系统的可靠性分析

1) 1#液压能源系统可靠性

1#系统运行时，要求所有部分都能正常工作，各部分组成一个串联系统。其中，泵源由EDP和EMP组成，1#系统正常工作时，由单发EDP驱动，当EDP故障失效时，由EMP作为备份能源进行运转，维持1#系统最低程度的运行。由此又可分析出1#液压能源系统的泵源部分是一个旁联系统，EDP为工作单元，EMP为储备单元。根据最小割集的算法，得出系统的逻辑功能图如图3所示。

图3 1#系统可靠性系统逻辑功能图

使用上述的逻辑框图，对1#系统可靠度进行分析如下。

(1) 防火关断阀、EDP以及EMP之间属于并联存在，防火关断阀与EDP之间属于串联存在，其可靠性Rs1计算如下：

Rs1=1-(1-REDP&FWSOV)(1-REMP)

=1-(1-e-λEDPte-λFWSOVt)(1-e-λEMPt)

(13)

其中,RFWSOV为防火关断阀可靠度；REDP为EDP可靠度；REMP为EMP可靠度；REDP&FWSOV为EDP与防火关断阀串联可靠度。

假设飞行时间以10 h为基础，可得其可靠性为：

Rs1=1-(1-e-4.80083/100000×10e-1.69865/100000×10)

(1-e-1.61769/100000×10)=0.999999894

(14)

即1#系统并联系统中参数可靠性为0.999999894。

(2) 针对一般串联系统，可以直接使用下列公式计算其可靠性：

(15)

(3) 1#系统可靠性R1，失效率λ1以及平均寿命θ1计算：

可得失效率参数为：

由此得到平均寿命为：

(4) 重要度计算：在进行了必要的参数计算以后，还需要进行系统的概率重要度PI计算，进而确定参数的重要性，并对重要度高的参数进行重点监控。

按照重要度的计算，可以得到1#系统的重要度为：

PI1=g1(t)=1-R1=1-Rs1R4，…，R11

=1-{[1-(1-RFWSOVREDP)

(1-REMP)]R4，…，R10}

(17)

按照上述计算，可以得到：

g1(t)=1-{[1-(FEDP+FFWSOV-FEDPFFWSOV)

FEMP](1-F4)，…，(1-F10)}

(18)

因此对于该系统，可以获得不同参数对于顶部事件发生概率的重要度是不同的，通过分别计算可以得到油箱的重要度计算，应该为：

(1-F回油油滤)

(19)

可以获得EDP的重要度为：Δg油箱=0.999188175

同理，可以分别得到其余的重要度获得如表3所示。

表3 1#系统重要度参数

通过上面计算得出的重要度，可以知道关键部件EDP以及EMP用为并联系统时，由于相互备份可靠度增强，其并联系统的重要度没有串联系统高。1#系统发生故障的概率最高的应该是高压油滤、油箱等串联结构。这就要求设计时除了选择合适的参数，还要提高元部件的可靠性，从而进一步提高飞机液压能源系统可靠性。

2) 2#液压能源系统可靠性

2#系统和1#系统类似，其中不同的是2#系统只使用1个EDP，而缺少一个EMP，以PTU代替，它将1#和2#进行联合。虽然PTU选择阀以及PTU都处于1#系统中，但是实际上却是2#系统的能量控制，因此将其归类到2#系统的逻辑框图中进行分析更加有效。获得2#系统的逻辑框图如图4所示。

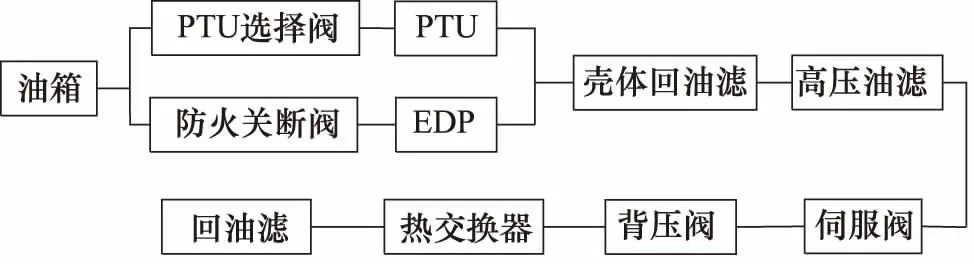
图4 2#系统逻辑框图

因此，2#系统中的并联部分是上述中PTU与EDP最小分割集的分析，其可靠度：

Rs2=1-(1-RPTU&VALVE)(1-REdP&FWSOV)

=1-(1-e-λPTUte-λVALVEt)(1-e-λEDPte-λFWSOVt)

=0.999999917

(20)

在此基础上，可以得到2#系统的可靠度为：

(21)

2#系统的重要度计算与1#系统相似，2#系统中几个关键元部件的重要度如表4。

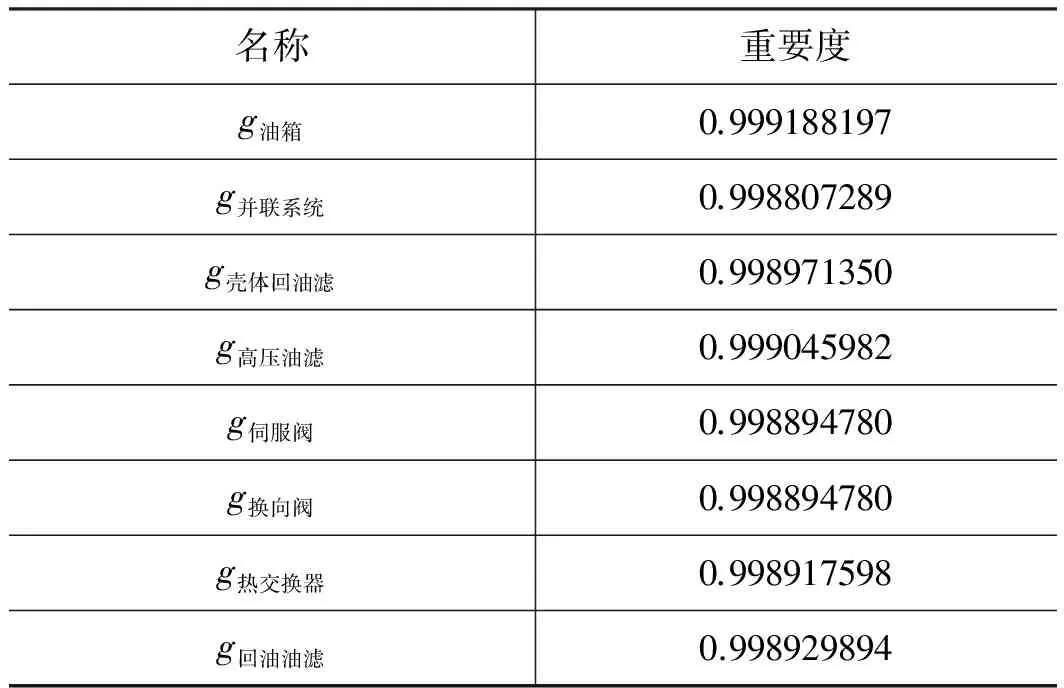
表4 2#系统重要度参数

3) 3#液压能源系统可靠性

3#系统的逻辑框图如图5所示，3#系统与1#系统以及2#系统类似，只是3#由两个EMP并联作为互相备份。

图5 3#系统逻辑框图

同时，3#系统与另外两个系统相互独立，3#系统可靠度所示：

4) 整体系统可靠性

基于以上单系统的可靠性分析计算整个飞机液压能源系统的可靠性，其中1#以及2#属于冗余系统，但是在分析失效树的时候已经将PTU考虑进去[11,12]，可以化简为和与3#形成并联系统。如图6所示。

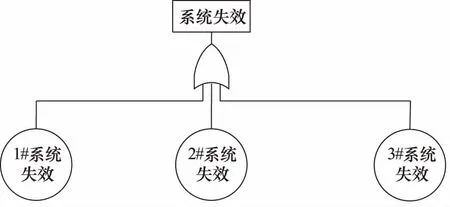
图6 系统失效树

整套系统可靠性为：

R=1-(1-R1)(1-R1)(1-R3)

=0.999999998

(23)

得到失效率为：

(24)

无故障失效时间为：

(25)

可以看出该飞机的平均无故障失效时间很大，按照飞机液压能源系统计算得出的安全时间是很完善的。一般而言，如果可靠度达到99.7%以上，可以认为满足飞机的要求。此外计算得出的平均无故障时间，可以用于与其他飞机作为对比的数据，但是并不能完整作为最后的分析结果。因为飞机飞行需要获得的无故障飞行时间，并不仅仅依靠飞机液压能源系统，还必须结合电气，机械结构等一起考虑。

3 A320以及B737可靠性分析

为了进一步对比飞机液压能源系统的可靠性，选择A320以及B737进行可靠性对比分析。按照前面提到的参数假设进行设置，并假设系统在相同元部件安全时间下进行计算，同时不考虑对多出的元器件进行分析。

对于A320，该液压体系系统与上面分析的不同点在于，其最后一个系统使用RAT进行参数备份。仅仅分析不同框架下的参数区别，不考虑RAT的参数备份。因此，认为A320与上述设计的参数相同，区别在于其系统备份构成不同。A320的系统构成可以表示为7所示。

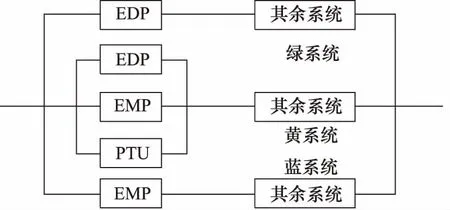
图7 A320可靠性系统构成框图

对于B737，该液压体系系统与上面分析的不同点在于，其三个系统中的A，B系统均使用EDP以及EMP，备用系统使用一个EMP进行备份。A，B之间使用PTU相连，因此可以获得三个系统的可靠性，其系统构成框图如8所示。

图8 B737可靠性构成系统框图

A320和B737液压系统可靠性数据如表5所示。

表5 A320和B737可靠性参数

通过上述对比，可以获得平均无故障时间：θ>θB737>θA320，即本研究中提出的民机液压系统平均无故障失效时间是最长的，可靠度是最高的[8]。

4 结论

(1) 本研究给出了一种适用于飞机液压能源系统元部件失效率的威布尔分布方法。

(2) 通过计算分析，获得了某型民机液压系统的可靠性， 同时得出了A320、 B737的可靠性。 通过对

比，可知本研究提出的民机液压系统的可靠性要高于A320和B737。

参考文献：

[1] O′ Connor P, Kleyner A. Practical Reliability Engineering[M].John Wiley & Sons,2011.

[2] 董传阳.民机液压原理性验证系统研究[D].杭州：浙江大学,2014.

[3] 孙小宇.可靠性在民用飞机维修工程中的应用研究[D].昆明：昆明理工大学,2006.

[4] Gupta R D,Kundu D.Theory & Methods: Generalized Exponential Distributions[J].Australian & New Zealand Journal of Statistics,1999,41(2):173-188.

[5] Kurtis,Fink D.,John,等.数值方法[M].北京：电子工业出版社,2002.

[6] 傅惠民,高镇同.确定威布尔分布三参数的相关系数优化法[J].航空学报,1990,11(7):323-327.

[7] 凌丹.威布尔分布模型及其在机械可靠性中的应用研究[D].成都：电子科技大学,2011.

[8] 王俊晖.民用飞机液压系统可靠性分析[D].杭州：浙江大学,2015.

[9] 黄长艺.机械工程测量与试验技术[M].北京：机械工业出版社，2000.

[10] 余国林,吴海桥,丁运亮.威布尔分布在飞机系统使用可靠性评估中的应用[J].航空维修与工程,2006,(2):49-51.

[11] Ming-li H E, Xiao-dong X, Yin-liang G. New Approach on System Reliability Distribution by Component Importance in FTA[J]. Safety and Environmental Engineering, 2009, 4(16): 62-65.

[12] Bao-Wei S, Zhao-Yong M, Wen-Qin W. Reliability evaluation method of torpedo based on FTA[J]. Journal of System Simulation, 2007, 19(10): 2180-2182.