伴随矩阵的若干性质及其在解题中的应用①
张丽丽
(陇东学院数学与统计学院,甘肃 庆阳745000)
0 引 言
伴随矩阵在矩阵运算中起着非常重要的作用,它是由方阵A 唯一确定的,因此伴随矩阵A*与原矩阵A 必定存在着一定的联系,在高等代数中我们已经详细的学习了矩阵的性质,这些性质能否平行的运用到伴随矩阵中来,伴随矩阵是否还有它自身的一些性质,下面将逐一进行探讨.
1 伴随矩阵的定义

2 伴随矩阵的性质
定理[2]n 阶矩阵A 可逆的充要条件是A 非退化,即,且
推论[3]AA*=A*A=|A|E,E 为n 阶单位矩阵.
性质1 设A 为n 阶矩阵,则有

证明: 若r(A)=n 时,矩阵A 可逆,由定理得r(A-1)=r(A)=n,即有r(A*)=n;
若r(A)=n-1 时,也就是A 中有n-1 阶非零子式,A*中有非零元素,从而r(A*)≥1.由定理得|A|=0,即AA*=| A| E =0.故r(A)+r(A*)≤n,再由r(A)=n-1 得r(A*)≤1,因此r(A*)=1.
若r(A)<n-1 时,则A 中所有n-1 阶子式全为0,即A*为零矩阵,故r(A*)=0.
性质2 设A 为n 阶矩阵,则|A*|=|A|n-1.
证明: 当A 可逆时,因为A*=|A|A-1,故|A*|=|A|A|-1|=|A|n|A|-1=|A|n-1.当A 不可逆时,|A|=0,故|A*|=0,可得|A*|=|A|n-1.
性质3 A*可逆当且仅当A 可逆,若A 可逆,则(A*)-1=(A-1)*.
证明:(A*)-1=(| A| A-1)-1=| A| A,(A-1)*=| A| (A-1)-1=| A|-1A,故(A*)-1=(A-1)*.
性质4 (A*)T=(AT)*
证明:(AT)*=|AT|(AT)-1=|A|(A-1)T=(|A|A-1)T=(A*)T
性质5 设k 为常数,(kA)*=kn-1A*.
证明:(kA)*=| kA| (kA)-1=kn| A|·k-1A-1=kn-1A*
性质6 (AB)*=B*A*.
2)|A|=0,|B|=0 时,令A(x)=xE+A,B(z)=xE+B,只要x 充分大,A(x)与B(x)都可逆,所以(A(x)B(x))*=(B(x))*(A(x))*.式中的元素都是关于x 的多项式,由于x 充分大时对应元素相等,所以对应元素是相等的多项式,即上式对任意x 都成立.取x =0 时,得(AB)*=B*A*.
性质7 若A 是可逆矩阵,λ 是其特征值,α 是A 的属于λ 的特征向量,那么A*的特征值为λ-1|A|,α 是A*的属于特征值λ-1|A|的特征向量.
证明: 因A 可逆,故λ ≠0,由Aα=λα,左乘A*得,A*Aα=λA*α,故A*α=λ-1|A|Eα=λ-1|A|α.
性质8 若A 是正定的,则A*也是正定的.
证明: 因A 正定,故存在可逆矩阵P,使PTAP=E,则有(PTAP)*=E*,即P*A*(PT)*=E,故A*也是正定的.
3 性质在解题中的应用
例1 设A 为4 阶方阵,且A 的伴随矩阵的行列式|A*|=8,求|A-1+A*|
解: 由性质2 得,|A|3=|A*|=8,故|A|=2 再结合定理得.
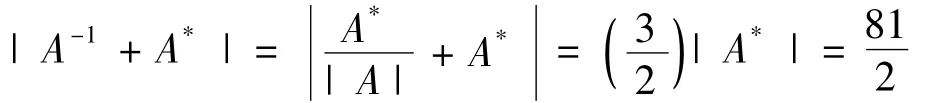

其中f 为多项式f(x)=2x2+x-1.由于相似矩阵有相同的特征值,故B 的全部特征值为,所以B-1的全部特征值为2,2,3.因此,f(B-1)的全部特征值为f(2)=9,f(2)=9,f(3)=20.
所以,所求行列式的值为D=f(B-1)=9×9×20=1620.
例3 设n 阶方阵A 是可逆的,那么A*可表示为A 的多项式.
解:A 的特征多项式为f(λ)=λn+an-1λn-1+…+a1λ+a0.因A 可逆,所以a0=(-1)n|A|0,由哈密尔顿-凯莱定理知f(A)=0,即An+an-1An-1+…+a1A+a0E=0 故
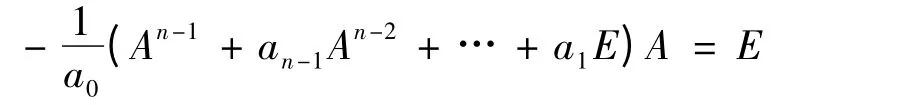
右乘A*,得

故
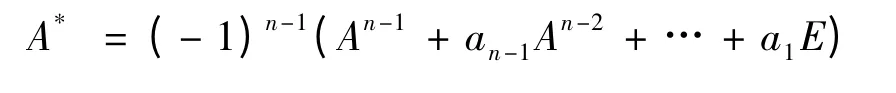
[1] 张禾瑞,郝丙新.高等代数[M].北京:高等教育出版社,1986.
[2] 吴天毅,王文杰,邱玉文.线性代数[M].天津:南开大学出版社.2007.
[3] 钱吉林.高等代数题解精粹[M].北京:中央名族大学出版社.2002.

