实对称矩阵特征值的一种在几何学上的应用①

孙卫卫

(青岛理工大学琴岛学院山东青岛266106)

0 引 言

对于形如二次曲线

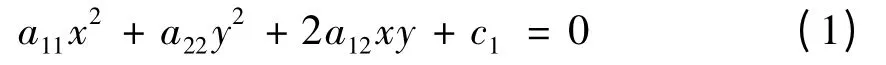
与形如二次曲面

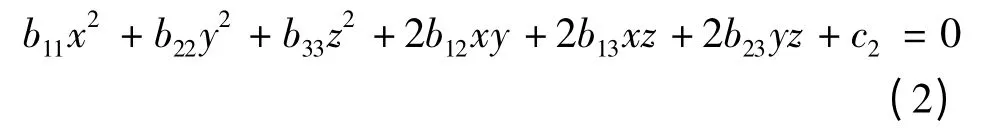
由于方程形式的特殊性，即不含有一次项，因此从其特殊性出发，得到了由实对称矩阵特征值与方程当中的常数项取值相结合来对它们形状推断的一种方法，体现了特征值的一种几何应用.

1 形如a11x2+a22y2+2a12xy+c1=0 的二次曲线的形状的推断

引入实对称矩阵:

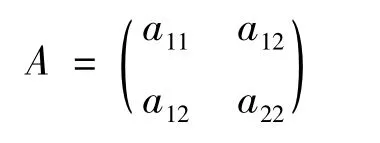
λ1，λ2为A 的特征值，得到如下定理:

定理1: 形如二次曲线

的形状，由λ1，λ2及c1的取值唯一确定.

证: 引入向量:

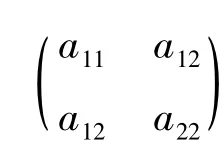
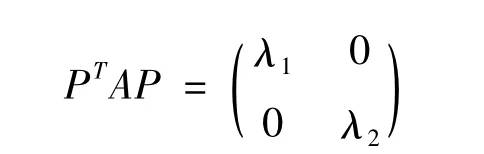
其中λ1，λ2为A 的特征值，做正交变换X=PY，则有，从而得0，即:

由于X=PY 为正交变换，而正交变换具有保持向量的内积与长度不变的性质，因此可知(1)式与(3)式所表示的二次曲线的具有相同的形状.故a11x2+a22y2+2a12xy+c1=0 所表示的二次曲线的形状由λ1，λ2及c1的取值唯一确定.

证毕.

例1: 下列方程分别表示怎样的曲线:

(1)x2+y2－xy－1=0;

(2)x2+y2+4xy+2=0.

解:(1)x2+y2－xy－2=0 所对应的实对称矩阵为

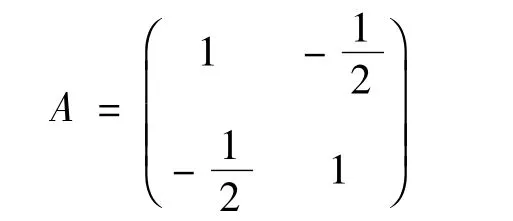
(2)x2+y2+4xy+2=0 所对应的实对称矩阵为

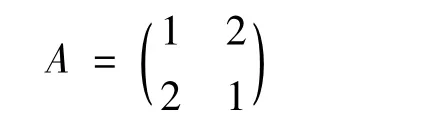
通过计算其特征值为λ1=3，λ2=－1，x2+y2+4xy+2=0 形状等同于3x2－y2+2=0 的形状，因此表示双曲线.

将定理1 的结论进行推广，得如下一类二次曲面形状推断的一种方法.

2 形如b11x2+b22y2+b33z2+2b12xy+2b13xz+2b23yz+c2=0 的二次曲面的形状的推断

引入实对称矩阵

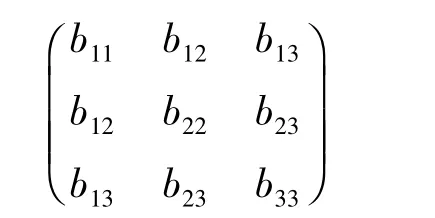
λ1′，λ2′，λ3′为B 的特征值，得到如下定理:

定理1: 形如二次曲面

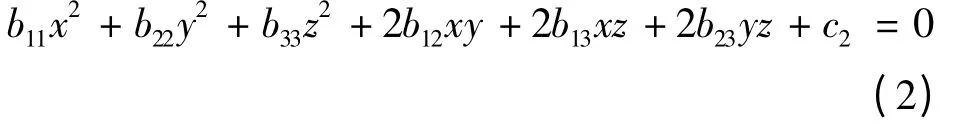
的形状，由λ1′，λ2′，λ3′及c2的取值唯一确定.

证: 引入向量:

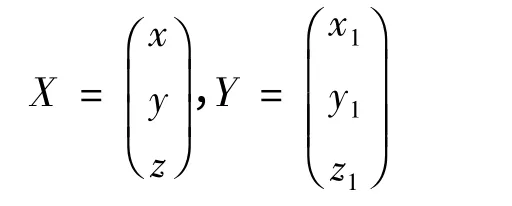
(3)式可等价于XTBX+c2=0，由于B 为实对称矩阵，一定存在正交矩阵P，有，

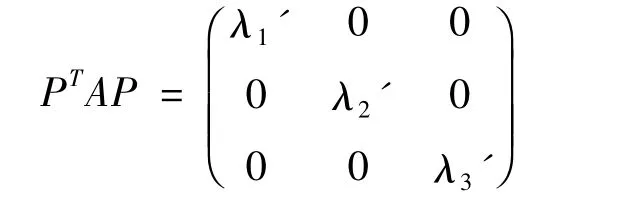
其中λ1′，λ2′，λ3′为B 的特征值，做正交变换X=PY，则有YTPTAPY+c2=0，从而得，

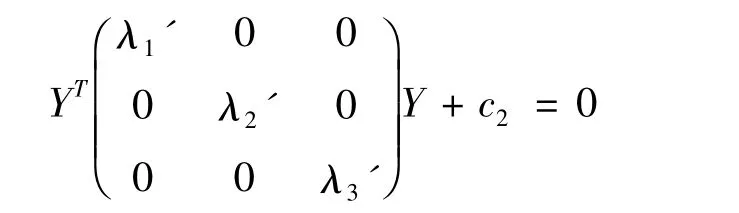
即:

由于X=PY 为正交变换，因此可知(2)式与(4)式所表示的二次曲面的具有相同的形状.故b11x2+b22y2+b33z2+2b12xy+2b13xz+2b23yz+c2=0 所表示的二次曲面的形状由λ1′，λ2′，λ3′及c2的取值唯一确定.

证毕.

例1: 下列方程分别表示怎样的二次曲面:

(1)x2+y2－2xz+1=0;

(2)x2+2y2+3z2－4xy－4yz－2=0.

解:(1)x2+y2－2xz+1=0 所对应的实对称矩阵为

(2)x2+2y2+3z2－4xy－4yz－1=0 所对应的实对称矩阵为

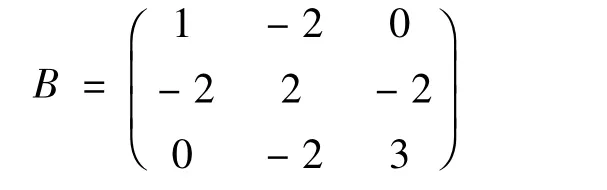
通过计算其特征值λ1=2，λ2=4，λ3=4，x2+2y2+3z2－4xy－4yz－2=0 形状等同于2x2+4y2+4z2－1=0 的形状，因此表示椭球面.

［1］ 同济大学数学系.高等数学(下册)［M］.第六版.北京:高等教育出版社，2007.

［2］ 华东师范大学数学系.数学分析(下册)［M］.第四版.北京:高等教育出版社，2010.

［3］ 徐森林.数学分析(第三册)［M］.北京:清华大学出版社，2007.

［4］ 吴赣昌.线性代数(理工类第四版)［M］.北京:中国人民大学出版社，2011.

［5］ 黄益生.高等代数［M］.北京:清华大学出版社，2014.

［6］ 杨文茂.空间解析几何［M］.武汉:武汉大学出版社，2004.