素环Jordan 理想上的右(θ，θ)－导子①

苑智莉

(吉林师范大学研究生院，吉林 长春130000)

0 引 言

Bell 和Kappe 证明了，d 为R 上导子，在R 上非零右理想上作为同态或反同态，则d = 0［1］.Rehman 进一步研究素环非零理想上广义导子作为同态或反同态，若d ≠0，则R 为可交换的［2］.Ashraf 推广到δ:R →R 左(θ，θ)－导子在素环Jordan 理想上作为同态或反同态，则δ=0［3］探究了Ashraf 的结果在右(θ，θ)－导子上是否成立.

1 预备知识

定义1: 如果对任意的a，b ∈R，aRb=0 有a=0 或b=0，则称R 为素环.

定义2: 设R 是结合环，d:R →R 是R 上可加映射，如果对于任意x，y ∈R，有d(xy)=d(x)y+xd(y).则称d 为R 上的一个导子.

定义3: 环R 的一个可加子群J 称为环R 的Jordan 理想，如果u ◦r ∈J，对∀u ∈J，r ∈R 成立.

定义4:S 为环R 的非空子集，θ，φ 为R 上自同构，可加映射δ:R →R 若满足δ(xy)=θ(x)δ(y)+φ(y)δ(x)，x，y ∈S，则称δ 为左(θ，φ)－导子.

由左(θ，φ)－导子的定义，类似的，定义右(θ，φ)－导子.

定义5:S 为环R 的非空子集，θ，φ 为R 上自同构，可加映射δ:R →R 若满足δ(xy)=δ(x)θ(y)+δ(y)φ(x)，x，y ∈S，则称δ 为右(θ，φ)－导子.

2 主要结果

引理1［［3］引理2.5］:R 为2－扭自由素环，J 为R 上非零Jordan 理想，若aJ=(0)或Ja=(0)，a ∈R 则a=0.

引理2［［3］引理2.6］:R 为2－扭自由素环，J 为R 上非零Jordan 理想，若aJb=(0)，则有a=0 或b=0.

定理1:R 为2－扭自由素环，J 为R 上非零Jordan 理想且为R 上子环，θ 为R 上自同构，δ:R →R 右(θ，θ)－导子，若δ 作为J 上同态，则δ=0.

证: 由已知

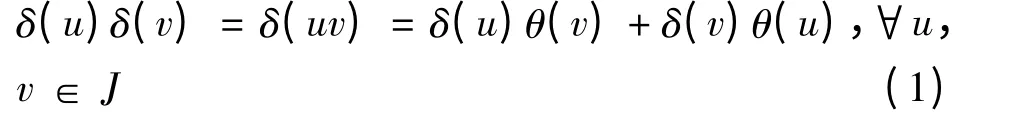
在(1)中，用uv 代替v，并应用(1)，可得δ(u)δ(u)θ(v)=δ(u)θ(uv)，∀u，v ∈J.所以

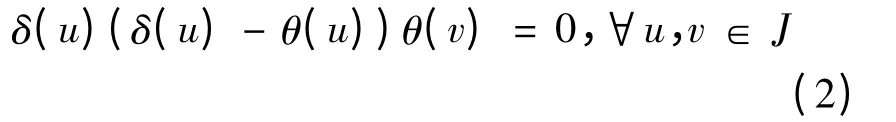
则δ(u)(δ(u)－θ(u))θ(J)=0，∀u ∈J.θ为自同构，J 为R 上非零Jordan 理想，θ(J)也为R上非零Jordan 理想，由引理1 可知，δ(u)(δ(u)－θ(u))=0，∀u ∈J.

则δ(u2)=δ(u)θ(u)，∀u ∈J.因为δ 为右(θ，θ)－导子，可得

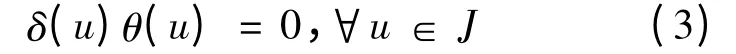
对(3)进行线性化，令u=u+v，可得

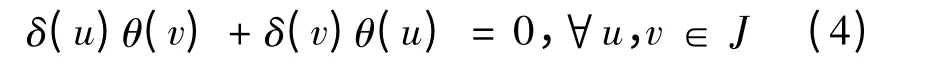
在(4)式中，vu 代替v，可得δ(u)θ(v)θ(u)=0，∀u，v ∈J.即θ－1(δ(u))Ju=0，∀u ∈J，由引理2 可知u=0 或θ－1(δ(u))=0.

当u=0 时，θ－1(δ(u))=0;当θ－1(δ(u))=0，即δ(u)=0，∀u ∈J.

令u=u ◦r 可得2δ(u)θ(r)=0，∀u ∈J，r ∈R

R 为2－扭自由素环，θ(J)为R 上非零Jordan理想，由引理1 可知δ(u)=0.

得证.

［1］ H.E.Bell and L.C.Kappe，Rings in Which Derivations Satisfy Certain Algebric Conditions［J］.Acta Math.Hung.1989，53:339－346.

［2］ M.Ashraf，N.Rehman and M.A.Quadri，On(σ，τ)－derivations in Certain Classes of Rings［J］.Rad.Math.1999，9，187－192.

［3］ Zaidi，S.M.A.，Ashraf，M.And Ali，S.:On Jordan Ideals and Left－Derivations in Prime Rings［J］.International Journal of Mathematical Sciences，2004，37:1957－1964.

［4］ N.Rehman，On Generalized Derivation as Homomorphisms and Anti－homomophisms［J］.Glasnic Mat.2004，39(59):27－30.

［5］ I.N.Herstein，Topics in Ring Theory［M］.Univ.Chicago press，Chicago 1969.