电动汽车换电网络协调规划

潘樟惠 高赐威,2

电动汽车换电网络协调规划

潘樟惠1高赐威1,2

（1.江苏省智能电网技术与装备重点实验室(东南大学) 南京 210096 2.东南大学成贤学院电气工程系 南京 210088）

基于电池租赁的换电模式是应对电动汽车规模化发展的一种可行的商业模式，但是当前对换电网络中各个单元的协调规划问题缺乏相应的理论指导。本文首先对换电网络中各个单元进行独立规划，分析了电池数量、物流能力与配送方案的关系，对换电网络运行方式进行了讨论，并基于换电网络运行方式优化建立起换电网络协调规划模型。模型以电池组缺额最小为换电网络运行方式优化目标，并以换电冗余度为判断准则，以最小化各个单元的调整成本为目标，对换电网络进行协调规划。通过算例分析验证了模型的有效性，对权重系数的分析可以为换电网络各单元之间的博弈提供指导。

电动汽车 换电网络 协调规划 运行方式 换电冗余度

1 引言

随着能源和环境危机的日益加剧，新能源汽车以节能环保的优势，成为我国七大战略新兴产业之一[1]。并于《电动汽车科技发展“十二五”专项规划》中确立了以“纯电驱动”电动汽车作为新能源汽车技术的发展方向和重中之重。基于电池租赁的换电模式，并配合包括电动汽车集中型充电站、配送站在内的智能充换电网络建设是应对电动汽车规模化发展的一种可行的商业模式[2-3]。通过集中型充电站承担大规模的电池充放电功能，并及时将满电池通过物流车辆配送至各个配送站，以满足电动汽车用户的换电需求[4]。由此可见，在智能充换电网络的规划建设阶段，亟需解决的是电池数量规划、配送站规划、物流能力规划、集中型充电站规划等问题。

目前，对于电动汽车换电网络规划的研究已涉及多个方面。文献[5]以配送站的建设成本、用户在换电途中的耗时成本和电池配送成本最小为目标建立了配送站的选址定容模型，并给出各个配送站的服务区域。文献[6]将电池组需求规划分为远期和近期两个阶段，远期规划适合于做年度电池数量规划，近期规划则基于最大日换电需求预测曲线建立考虑电池数量和物流能力的综合规划模型。文献[7]在配送站位置和所需电量已知的情况下，通过计算配送站的重心得到集中型充电站的位置和配送范围，但未考虑投资成本、交通等因素。文献[8]提出了综合考虑集中型充电站建设和运行成本的集中型充电站最优容量规划模型。文献[9]以年设备费用最小为目标函数，以换电服务的日可用率等为约束条件，建立了电池和充电设备数量的优化配置模型。文献[10]以用户更换电池的总加权距离最短为目标确定配送站的位置，并以包含配电网在内的集中型充电站建设、运营维护成本最低为目标得到集中型充电站的选址定容和服务范围。文献[11]将集中型充电站的规划与配电网调度相结合，建立了考虑集中型充电站的经济性和对配电网考虑削峰填谷作用的集中型充电站选址定容二层规划模型，并将加权伏罗诺伊图应用于集中型充电站服务区域的划分，实现集中型充电站负载率的均衡。

然而，换电网络中任何一个单元都不是独立运行的，任何一个单元的规划配置都会对其他单元的性能造成影响，且换电网络的各个单元可能分属于不同公司，往往以自身利益为中心进行规划，忽视了换电网络的整体效率。因此，单个单元的最优规划往往不一定能达到整体的最优，建立各个单元独立规划模型的同时必须考虑各单元规划的协调问题。然而，目前相关文献的研究都集中于对换电网络中各个单元的独立规划，并没有考虑到对换电网络中各个单元的规划进行协调。鉴于此，本文首先对换电网络中各个单元进行独立规划，并建立起基于运行方式优化的换电网络协调规划模型。

2 换电网络各单元独立规划模型

2.1配送站规划

假设根据某一地区的换电需求和配送站的服务半径已经得到某一地区内配送站的位置和容量，并由此可进一步通过每一个配送站在每一时刻的换电需求得到一天内集中型充电站在每一时刻的换电需求。

2.2电池数量规划

在待规划的区域内，假设人口数量为R，平均每人电动汽车拥有率为α，采用换电方式的比例为β；电动汽车日行驶里程的期望值为E；电动汽车每充满一次的行驶里程为L，电动汽车的车载电池组数量为nevb。

若不考虑电池在一天当中的重复利用，并假设集中型充电站的充电容量总能满足该地区每天的换电需求，由此可得到一个区域内平均每天需要更换的电池组数量为:

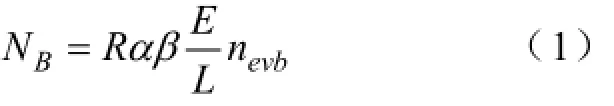
2.3物流能力规划

假设采用招标的方式选择某一物流公司对电池进行配送，假设该物流公司共有物流车辆数ncar，物流车队中所有车辆的最大装载量相同为Qcar，则物流公司的最大运送能力为

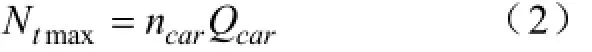
2.4集中型充电站容量规划

假设通过采用2.2节中的规划方法得到所需要配置的电池数量NB，并假设集中型充电站每天只配送一次，故集中型充电站需按电池组的最大需求量来进行充电。

假设集中型充电站内的充电设备套数为NE，一套充电设备包含一台变压器及所属的ncharge台充电机，一台充电机可同时满足nb块电池组串联充电，则集中型充电站最大可满足Nbmax=NE·ncharge·nb块电池组同时充电。假设一个电池组的充电时长为Tcharge，则集中型充电站至少需配置的充电设备套数为:

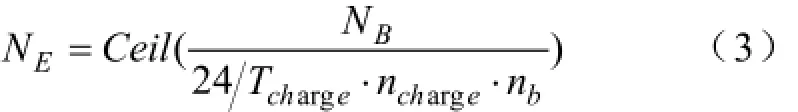
式中，Ceil( )表示向上取整。

3 换电网络运行方式

3.1物流能力、电池数量与配送方案的关系

统计各个配送站在每个时刻的换电需求（更换电池组需求）可以得到某地区一天内的换电曲线，如图1所示。由于物流车辆到达配送站需要一定的时间，因此在配送时所考虑的配送量是从物流车辆到达配送站的时刻到下一次配送到达配送站这段时间内的换电需求，根据配送时间可以得到配送曲线，如图2所示。

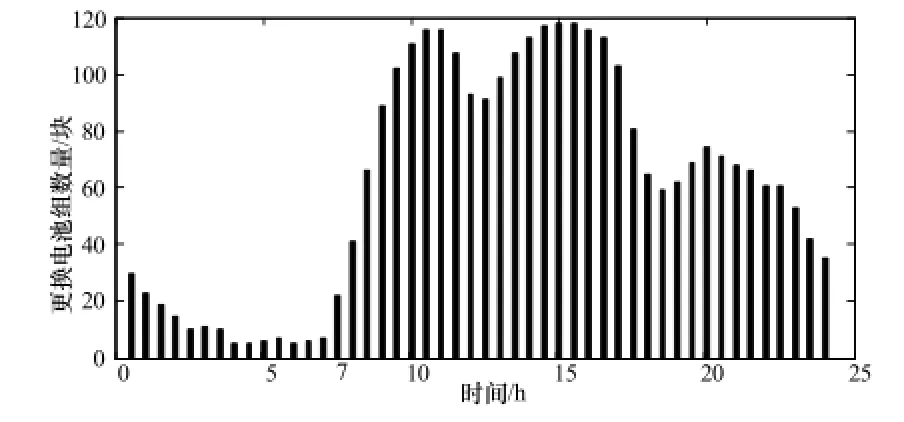
图1 某地区一天的换电曲线Fig.1 The battery-swapping curve of a day in a certain region

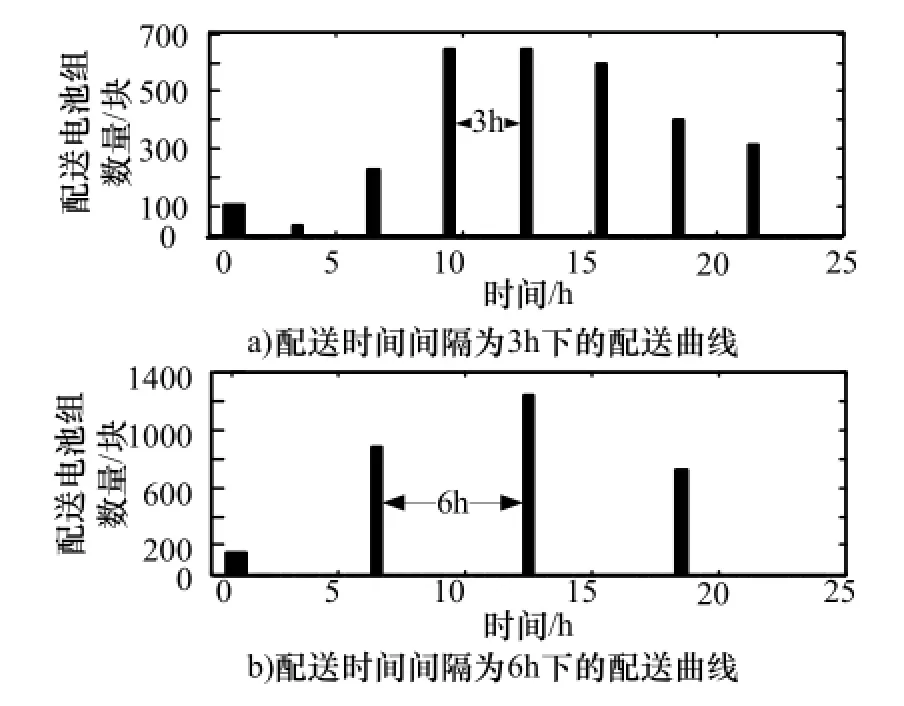
图2 不同配送时间间隔下的配送曲线Fig.2 The delivery curve under different time intervals

配送曲线随着配送方案的不同而发生变化。例如，当配送时间间隔分别为3h和6h时，从图2可以看出，随着配送时间间隔的增大，配送次数的减少，每次所需配送的电池组数量显著增多，且相邻两次所需配送的电池组数量相差越大，所需的物流车辆数也相差越大。

从物流公司的角度考虑，如果每次所需物流车辆数相差较大，则会对物流公司车辆的调度和车辆的利用率产生不利影响，且若单次所需配送量过多，则物流公司的物流车辆数可能满足不了需求，因此物流公司希望每次所需的物流车辆尽量相等。

从电池租赁商的角度考虑，假设每次配送运回集中型充电站的空电池均能在下一次配送之前充满，则电池租赁商应至少需要按一天内要满足的单次最大配送量来配置电池数量，如果每次所需配送的电池组数量相差较大，则增大了租赁电池组的费用，同时降低了电池的循环利用率。因此，通过使每次配送的电池组数量尽量相等可以减少租赁电池组的费用。

综上分析，物流公司和电池租赁商均希望每次配送的电池组数量尽量相等，而以最小化租赁电池组数量为目标的电池数量规划和以每次所需物流车辆尽量相等为目标的物流能力规划又等同于通过调整配送时间和配送次数使得每次所需配送的电池数量尽量相等。因此电池数量规划和物流能力规划的目标是一致的，本文以最小化租赁电池组数量为目标对电池数量和物流能力进行规划。

3.2换电网络运行方式

换电网络的运行方式对各个单元的规划配置能否满足换电需求具有重要影响。对于特定的一种换电网络规划配置，有可能于一种运行方式下可以满足换电需求，而于另一种运行方式下则可能就满足不了换电需求。因此，不考虑换电网络的运行方式对其进行规划是不科学的，寻求特定的换电网络规划配置下尽量能满足换电需求的运行方式或对于特定的运行方式下调整各个单元的规划配置使其能满足换电需求是需要解决的问题。因此，本文先对换电网络运行方式进行讨论，然后建立起换电网络协调规划模型。

3.2.1 换电需求

采用所有预测日在每一时刻换电需求的最大值得到该周/月的最大换电需求曲线Lmax(t1,t2,…,tn)[6]。则一天当中物流车队负责的配送站总的换电需求为：

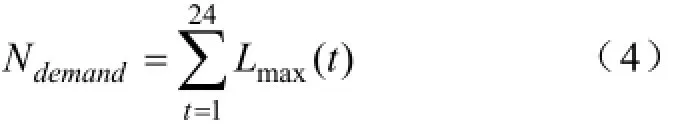
3.2.2 配送方式

假设一天内配送次数为Ndis，则配送次数的范围为：

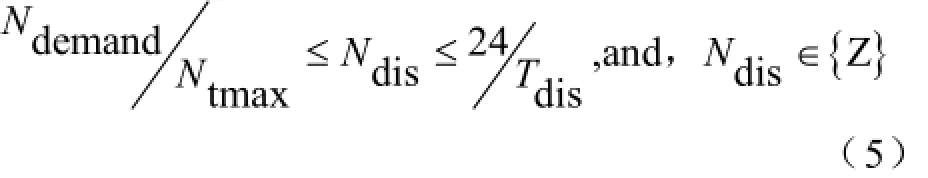
式中，Tdis表示单次配送所需时间，即从集中型充电站出发至返回到达集中型充电站所需的时间。

假设每次配送车辆从集中型充电站出发的时刻（即配送时刻）为ti，则配送时刻需满足的约束条件为:

第i次配送时的换电需求为：

3.2.3 物流能力

根据确定的配送数量可以得到需要的物流车辆数:

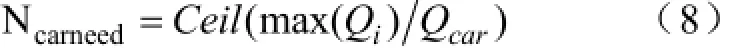
一般情况下，所需要的物流车辆数Ncarneed小于物流公司所拥有的车辆数Ncar，当物流公司满足不了配送需求时，则需要考虑调整配送方式或选择物流能力更大的物流公司。

3.2.4 电池集中充电策略

物流车辆将满电池组从集中型充电站运到配送站，并同时将空电池组从配送站运回到集中型充电站进行集中充电。考虑到电池组管理和配送的方便，对电池组的充电从每次配送返回到达集中型充电站内开始，忽略电池的装卸等时间。一天当中的可充电时段根据相邻两次配送返回到达集中型充电站的时刻确定，如图3中的TC2、TC3、TC4。在可充电时段内，又可根据电池组充满电所需的时间Tcharge划分为几个充电周期，如图中的C1、C2、C3。当可充电时段内的剩余时间小于Tcharge时，则不再对电池组进行充电，等到下一个可充电时段再对其充电。图中，ti为第i次配送时刻，ti+Tdis表示第i次配送返回到达集中型充电站的时刻。

图3 电池集中充电策略Fig.3 The centralized charging strategy of batteries

在第i-1次配送运回和第i次配送运出之前这段时间内，集中型充电站的最大可充满电池数为:

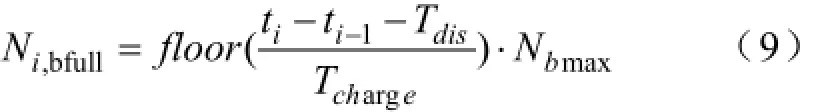
式中，floor( )表示向下取整。

则第i次配送运出时集中型充电站内的空电池数为:

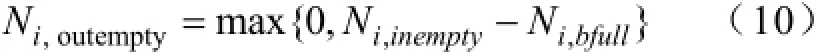
式中，Ni,inempty为第i-1次配送运回时（即第i个可充电时段的开始时刻）集中型充电站内的空电池数。

第i次配送将运出时集中型充电站内的满电池组数量为:

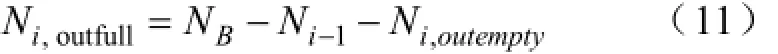
式中，Ni-1是第i-1次的实际配送量。

则第i次配送时的实际配送量为:

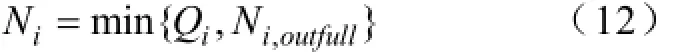
表示第i次配送时的实际配送量与配送站的换电需求、集中型充电站内的满电池组数量密切相关，为两者的最小值。

在第i-1次配送运回和第i次配送运回之前这段时间内，集中型充电站的最大可充满电池数为:

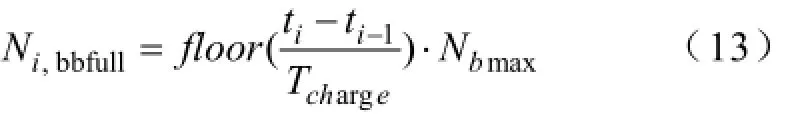
第i次配送运回的空电池数为第i-1次配送运出的电池数Ni-1。则第i次配送运回后（即第i+1个可充电时段的开始时刻）集中型充电站内的空电池数为:

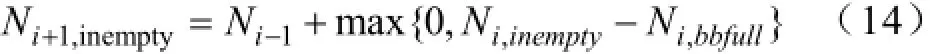
4 基于运行方式优化的换电网络协调规划

4.1换电网络运行方式优化

对于已完成独立规划的换电网络各单元，对换电网络运行方式进行优化，求解使电池组缺额最小时的换电网络运行方式，如果能够满足换电冗余度要求，则不需要再进行协调规划，否则需要进行换电网络协调规划。

目标函数:

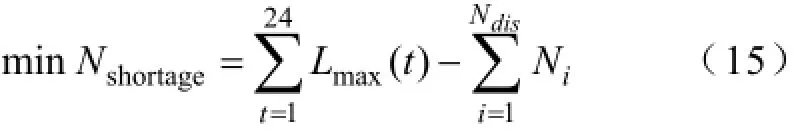
式中，Nshortage表示电池组缺额，求解为了使电池组缺额最小时的配送次数Ndis和配送时间Tdis。

定义第i次配送时的换电冗余度为第i次配送运出时集中型充电站的满电池数与第i次配送时的换电需求Qi之差除以第i次配送时的换电需求Qi，即:

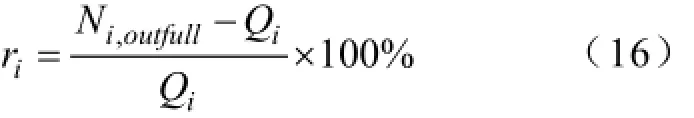
则换电网络规划是否能满足换电需求取决于一天当中的最小换电冗余度，即:

可以设定换电网络运行时需要的换电冗余度rset，当r＞rset，则换电网络规划结果有冗余，可以调整减小相应单元的规划配置；当r=rset，则换电网络规划结果刚好可以满足目标需求，不需要调整；当r＜rset，则换电网络规划结果不能满足目标换电需求，需要调整增大相应单元的规划配置。实际设置时，rset可为一大于等于0的值，本文中，取rset=0，当r≠rset时则需进行协调规划。

4.2换电网络协调规划

由每一个配送站在每一时刻的换电需求得到一天内集中型充电站在每一时刻的换电需求是后续确定换电网络运行方式并对电池数量规划和集中型充电站容量规划进行调整的基础，因此本文假设根据某一地区的换电需求和配送站的服务半径已经得到某一地区内配送站的位置和容量，并进一步得到一天内集中型充电站在每一时刻的换电需求。

由于r≠rset，假设电池数量和充电设备需要调整的量分别为ΔNB和ΔNE，以最小化各单元的调整成本为目标，则电池数量需要调整的目标函数为:

充电设备需要调整的目标函数为:

式中，CB、CE分别为电池、充电设备的单位成本系数。

由于电池和充电设备数量的分别调整均可影响换电冗余度，而电池的拥有者和充电设备的拥有者可能属于不同的公司，因此，引入权重系数α，代表两家公司的利益关系和话语权，可以根据双方的博弈结果进行赋值，将多目标优化问题转变成单目标优化问题，如下式所示:

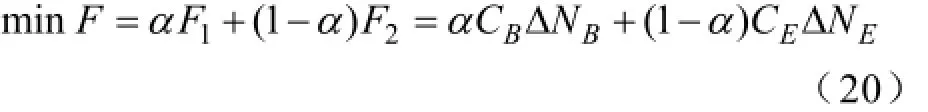
当电池和充电设备均属同一公司时，则上式中取α=0.5。

约束条件为满足换电需求:

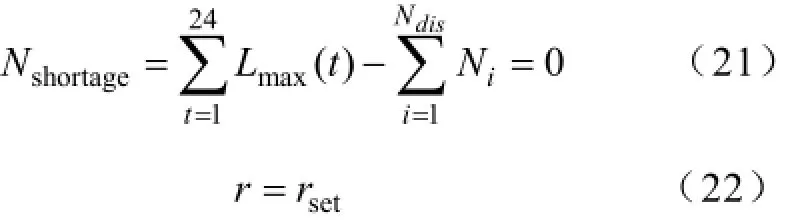
4.3模型求解

本文的目的是对已完成独立规划的换电网络各单元进行协调调整，因此首先对换电网络各单元进行独立规划，在此基础上求解为了使电池组缺额最小时的运行方式，若在此运行方式下不能满足换电需求或有冗余，则对换电网络进行协调规划，通过调整各单元的规划配置来满足换电需求。整个流程如图4所示。

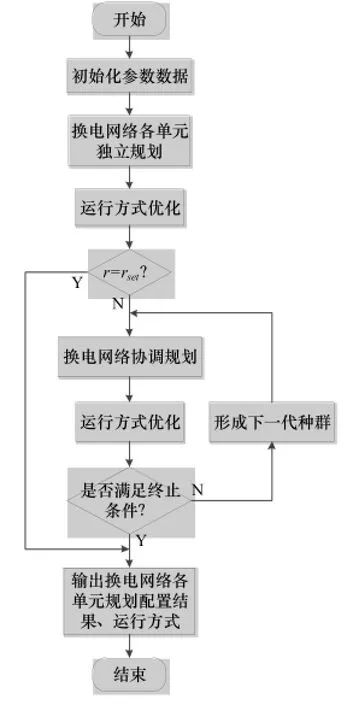
图4 换电网络协调规划流程Fig.4 Flow chart of coordinated planning of battery-swapping network

本文采用遗传算法对所建立的换电网络协调规划模型进行求解。

（1）染色体编码策略

为提高编码效率，染色体编码策略采用混合编码[12]。每条染色体分成3部分，如表1所示。

表1 染色体结构Tab.1 Chromosome structure

表示规划调整量的电池数量调整量ΔNB和充电设备调整量ΔNE均采用整数编码，运行方式则采用二进制编码。对于运行方式的编码，由于求解的是配送时刻，因此，设置运行方式部分的染色体长度为可选配送时刻点（本文以30min为最小时间间隔，则一天共有48个待选配送时刻点），当编码为1时表示在该时刻进行配送，为0表示不配送。同时，根据约束条件式（6），在形成染色体时，染色体中任意相邻的2个“1”之间所代表的时间间隔必须大于或等于单次配送所需时间Tdis，否则重新生成染色体。

（2）遗传操作

本文采用的遗传操作参数见表2。

表2 遗传操作参数Tab.2 Parameters of GA

5 算例分析

5.1换电网络各单元独立规划

5.1.1 配送站规划

假设根据某一地区的换电需求和配送站的服务半径已经得到该地区内配送站的位置和容量，并进一步通过各个配送站在每一时刻的换电需求得到一天内集中型充电站在每一时刻的换电需求，如表3所示。

表3 集中型充电站最大日换电需求Tab.3 The biggest daily battery-swapping demand of the centralized charging station

5.1.2 电池数量规划

假设在待规划的区域内某水平年的规划参数如表4所示[6]，根据式（1），可求得该区域内需要配置的电池组数量NB为2263块。

表4 某水平年规划参数Tab.4 Planning parameters of a level year

5.1.3 物流能力规划

假设配送车辆的最大装载量为3t，单块电池组质量为30kg，则一辆车的最大装载量Qcar为100块，假设物流公司共有物流车辆数ncar为10辆，则物流公司的最大运送能力Ntmax为1000块电池组。

5.1.4 集中型充电站容量规划

假设一套充电设备可满足5台充电机同时工作，一台充电机可同时满足6块电池组串联充电，一块电池组的充电时长Tcharge为2.5h。根据式（3），可得集中型充电站至少需配置的充电设备套数NE为8。在最小配置下，充电站最大可满足240块电池组同时充电。

5.2基于运行方式优化的换电网络协调规划

5.2.1 换电网络运行方式优化

换电网络各单元独立规划参数取5.1节中的参数，忽略物流车队在配送站及充电站装卸电池组所需时间，物流车队往返一次所需时间Tdis为3h。为使配送站内的换电需求能尽快得到满足，设定换电站运营的第1次配送起始时刻t1为0：00。假设第一天初始运营时集中型充电站内的满电池数为2 263块，为了进一步消除初始电量对运算结果的影响，连续进行两日的计算，并假设两日的换电需求曲线一致，考虑到次日的换电需求和运行方式，当日最后一次配送时所需的配送量为从tNdis+Tdis/2到次日Tdis/2这段时间内的换电需求，并以次日的计算结果为最终运行方式。求解得到使电池组缺额最小时的运行方式如表5所示。

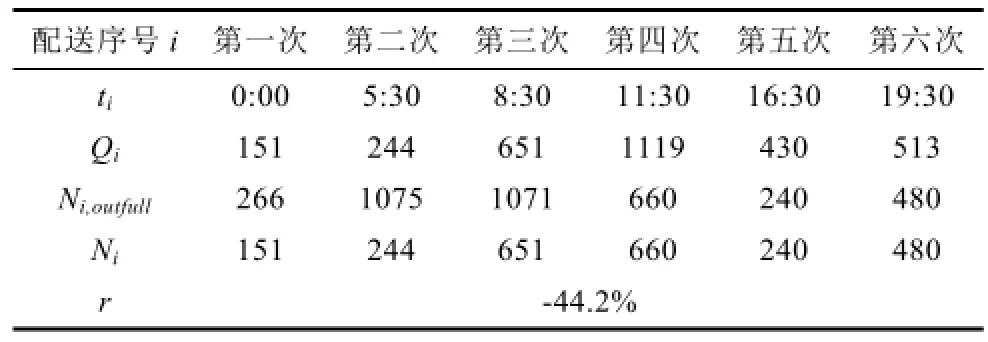
表5 运行方式优化结果Tab.5 The optimization results of the operation mode

由于r＜rset，说明投入不足，故需要通过协调规划调整各单元的规划配置。

5.2.2 换电网络协调规划

假设电池的单位成本系数CB为0.5万元/块，充电设备的单位成本系数CE为15万元/套，通过电池拥有者和充电设备拥有者的博弈得到权重系数α为0.4。采用遗传算法求解得到ΔNB为-270，ΔNE为4，即电池数量可减少270块后为1993块，而充电设备应增加4套后为12套。此时换电网络的运行方式如表6所示。

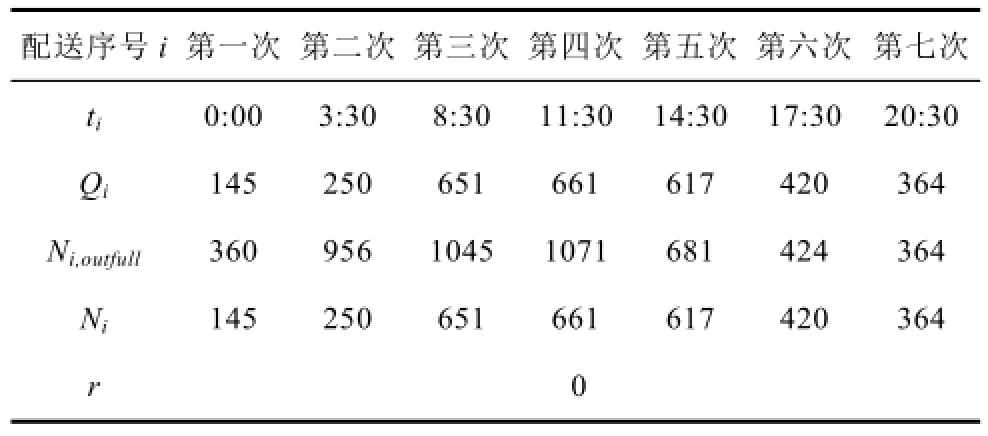
表6 换电网络协调规划后的运行方式Tab.6 The operation mode after coordinated planning of battery-swapping network

根据式（8）可求得所需的物流车辆数Ncarneed为7辆。

5.3权重系数α灵敏度分析

换电网络也可事先规定其运行方式，则在4.3节模型求解中不再对运行方式进行优化，而直接进行换电网络协调规划。假设事先规定一天内需配送5次，每次的配送时刻和所需的配送量如下表所示:

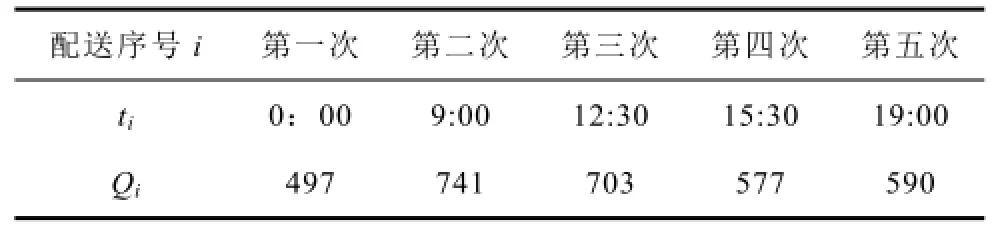
表7 事先规定的配送时刻和配送量Tab.7 The prespecified time and amount of delivery

采用5.1节中的相关参数得到在事先规定运行方式下的运行情况如下表所示:

表8 事先规定运行方式下的运行情况Tab.8 The operation condition of prespecified operation mode

由于r＜rset，说明投入不足，故需要通过协调规划调整各单元的规划配置。

权重系数α是影响换电网络协调规划结果的重要因素。对于上述已事先规定运行方式的情况下，当权重系数α从0.1变化到0.9时，电池数量调整量ΔNB和充电设备调整量ΔNE的变化情况如图5所示。

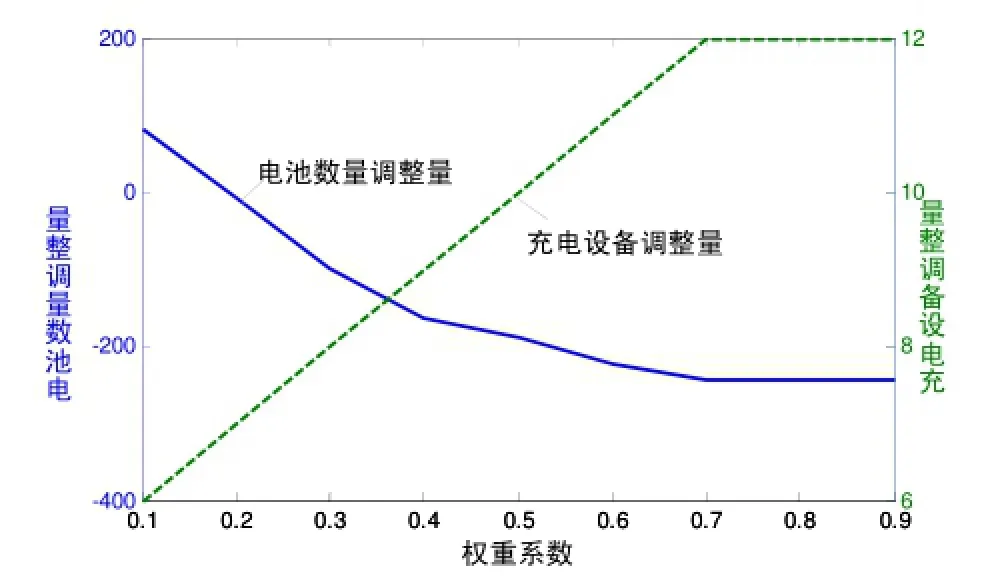
图5 不同权重系数α下电池与充电设备的调整量Fig.5 The adjustment of battery and charging device under different weighting coefficient α

从图5可以看出，随着权重系数α的增大，电池数量调整量ΔNB呈下降趋势，而充电设备调整量ΔNE逐渐增加，当权重系数α大于0.7后，两者不再变化，这是因为在该事先规定的运行方式下，在可充电时段内，充电设备已能满足对运回的全部空电池进行充电，没必要再增加充电设备，而如果再减少电池数量，则会满足不了换电需求。因此，对于换电网络的一种运行方式，相应的存在某一最少电池数量配置。另外，从图中可以看出，随着权重系数α的增大，充电设备调整量ΔNE呈线性增长的趋势，而电池数量调整量ΔNB则近似呈反比例递减趋势。对于权重系数α小于0.4时，增大权重系数α可以明显减少电池数量配置，因此，电池租赁商应尽可能争取使得权重系数α大于0.4，或以此为依据与充电设备拥有者进行利益协商。

6 结论

本文研究了电动汽车换电网络协调规划问题，为电动汽车换电网络规划提供了理论基础。通过对电池数量、物流能力与配送方案的分析发现电池数量规划和物流能力规划目标的一致性。基于换电网络运行方式优化建立了换电网络协调规划模型。通过该模型可以在考虑换电网络运行方式的情况下，以最小化换电网络各单元调整成本为目标，对换电网络进行协调规划。并定量分析了权重系数α对换电网络各单元调整量的影响，可以为换电网络各单元之间的博弈提供指导。

[1] 国务院关于印发“十二五”国家战略性新兴产业发展规划的通知[EB/0L]. 2012[2012-07-20]. http：//www. gov.cn/zwgk/2012-07/20/content_2187770.htm.

[2] 陈征, 刘念, 路欣怡. 考虑换电储备的电动汽车光伏换电站动态功率分配方法[J]. 电工技术学报, 2014, 29(4)： 306-315.

Chen Zheng, Liu Nian, Lu Xinyi, et al. Dynamic power distribution method of PV-based battery switch stations considering battery reservation[J]. Transactions of China Electrotechnical Society, 2014, 29(4)：306-315.

[3] 姚伟锋, 赵俊华, 文福拴, 等. 集中充电模式下的电动汽车调频策略[J]. 电力系统自动化, 2014, 38(9)： 69-76.

Yao Weifeng, Zhao Junhua, Wen Fushuan, et al. Frequency regulation strategy for electric vehicles with centralized charging[J]. Automation of Electric Power Systems, 2014, 38(9)： 69-76.

[4] 高赐威, 吴茜. 电动汽车换电模式研究综述[J]. 电网技术, 2013, 37(4)： 891-898.

Gao Ciwei, Wu Xi. A survey on battery-swapping mode of electric vehicles[J]. Power System Technology, 2013, 37(4)： 891-898.

[5] 熊虎, 向铁元, 荣欣, 等. 电动汽车电池更换站布局的最优规划[J]. 电力自动化设备, 2012, 32(09)：1-6.

Xiong Hu, Xiang Tieyuan, Rong Xin, et al. Optimal allocation of electric vehicle battery swap stations[J]. Electric Power Automation Equipment, 2012, 32(09)：1-6.

[6] 高赐威, 吴茜, 薛飞, 等. 换电模式下电动汽车电池组需求规划[J]. 电网技术, 2013, 37(07)： 1783-1791.

Gao Ciwei, Wu Xi, Xue Fei. Demand planning of electric vehicle battery pack under battery swapping mode[J]. Power System Technology, 2013, 37(07)：1783-1791.

[7] He Zhanyong, Zhou Yuhui, Liang Na, et al. The location studies of charging station for replacing batteries[C]. Advanced Power System Automation and Protection. Beijing, China, 2011： 2013-2017.

[8] 高赐威, 张亮, 薛飞, 等. 集中型充电站容量规划模型研究[J]. 中国电机工程学报, 2012, 32(31)：27-34.

Gao Ciwei, Zhang Liang, Xue Fei, et al. Study on capacity and site planning of large-scale centralized charging stations[J]. Proceedings of the CSEE, 2012, 32(31)： 27-34.

[9] Lu Xinyi, Liu Nian, Huang Yangqi, et al. Optimal configuration of EV battery swapping station considering service availability[C]. 2014 International Conference on Intelligent Green Building and Smart Grid (IGBSG), Taipei, 2014： 1-5.

[10] 李国, 张智晟, 温令云. 换电模式下电动汽车充换电网络的规划[J]. 电力系统保护与控制, 2013, 41(20)： 93-98.

Li Guo, Zhang Zhisheng, Wen Lingyun, et al. Planning of battery-switching and vehicle-charging network based on battery switching mode[J]. Power System Protection and Control, 2013, 41(20)： 93-98.

[11] 所丽, 唐巍, 白牧可. 考虑削峰填谷的配电网集中型充电站选址定容规划[J]. 中国电机工程学报, 2014, 34(7)： 1052-1060.

Suo Li, Tang Wei, Bai Muke, et al. Locating and sizing of centralized charging stations in distribution network considering load shifting[J]. Proceedings of the CSEE, 2014, 34(7)： 1052-1060.

[12] 白牧可, 唐巍, 张璐. 基于机会约束规划的DG与配电网架多目标协调规划[J]. 电工技术学报, 2013, 28(10)： 346-354.

Bai Muke, Tang Wei, Zhang Lu. Multi-objective coordinated planning of distribution network incorporating distributed generation based on chance constrained programming[J]. Transactions of China Electrotechnical Society, 2013, 28(10)： 346-354.

Coordinated planning of EV battery-swapping network

Pan Zhanghui1Gao Ciwei1,2
（1. Jiangsu Provincial Key Laboratory of Smart Grid Technology & Equipment (Southeast University) Nanjing 210096 China 2. Southeast University Chengxian College Department of Electrical Engineering Nanjing 210088 China）

The battery-swapping mode based on the battery lease is a viable business mode to deal with the large-scale development of electric vehicles (EV). There is lack of corresponding theoretical guidance for the coordinated planning of battery-swapping network between each unit. Firstly, independent planning model of each unit in the battery-swapping network was established. The relationship between the number of batteries, logistics capabilities and distribution scheme were researched. The operation mode of battery-swapping network was discussed. And then, the coordinated planning model of battery-swapping network based on the optimization operation mode was established. The operation mode was optimized by the target of minimizing the shortage of the batteries. And use the redundancy of battery-swapping as the judging criterion. After that, the coordinated planning of battery-swapping network was optimized by the target of minimizing the adjustment costs of each unit. The effectiveness of this model was tested by an example. The analysis of the weighting coefficient can provide guidance for the game between each unit in the battery-swapping network.

Electric vehicles(EV), battery-swapping network, coordinated planning, operation mode, the redundancy of battery-swapping

TM71

潘樟惠 男，1991年生，硕士研究生，研究方向为电力系统运行与控制。

国家自然科学基金项目（51207022），“青蓝工程”资助。

2014-07-10

高赐威 男，1977年生，博士，教授，博士生导师，研究方向为电动汽车接入电网、电力规划、电力市场、需求侧管理、电力安全等。