考虑储能参与快速调频动作时机与深度的容量配置方法

黄际元 李欣然 曹一家 刘卫健

考虑储能参与快速调频动作时机与深度的容量配置方法

黄际元 李欣然 曹一家 刘卫健

（湖南大学电气与信息工程学院 长沙 410082）

提出一种考虑储能参与快速调频动作时机与深度的容量配置方法。首先依据复频域灵敏度原理分析了含储能的区域电网的频率特性，基于此提出一种针对储能的综合控制模式，它包含了虚拟惯性控制和虚拟下垂控制模式。然后，基于时域灵敏度原理和调频评估指标，理论推导了储能在参与快速调频时的时域频率响应特性，分析了确定其合理动作时机应当满足的条件，结合此条件给出了相关动作时机及其应当采取的控制模式；同时，结合调频评估指标要求确定了动作深度，并给出了所必需的动作深度与额定功率之间的关系，进而形成了储能容量配置方法并给出了相应的流程。最后，以某典型电网的参考事故为初始条件进行了仿真验证，结果表明所提方法能以较小的储能配置容量实现调频评估指标要求。

储能 快速调频 时机 深度 容量配置

1 引言

风电等间歇式电源不具备传统电源的惯性响应特性，且出力具有波动性和不确定性特征，大规模接入电网后会显著加剧调频压力。当电网发生紧急（极端）事故（发电机突然跳闸或负荷突然增加）时，若调频储备启动时间过长或者容量不能满足事故需求，为防止频率严重越限，通常选择低频减负荷或者高频切机作为调节手段，如利用频率偏差变化率（简称频差变化率）继电器或频率偏差继电器进行电网保护，增加的频差变化率或频率偏差可能导致风电与电网解列（级联效应），严重故障可能导致连锁跳闸和区域解列，形成几个电气孤岛，从而使情况进一步恶化[1-2]。因此，确保电网中拥有足够的调频储备意义重大，而储能的快速响应特性使得其能成为有效的辅助调频手段。

国内外以电池为主的新型快速储能技术当前仍停留在示范阶段，且多用于改善风电场的联网运行性能，其广域调控效能未得到充分利用[3-4]。从电网运行需求全局角度，如何充分利用好储能参与快速调频是当今所面临的关键问题。文献[5]提出利用超级电容储能参与调频，定义了梯形状的功率响应曲线，由延时、上升时间、下降时间、额定功率持续时间和功率偏差五个指标确定；文献[6-7]提出利用电池储能参与调频，文献[6]在考虑储能过载特性(过载能力及对应的可允许的过载持续时间)的基础上设计出合适的控制策略，但未进行相关动作时机的分析，而文献[7]提出利用频率变化过程中频差变化率和频率偏差绝对值最大值为决策变量，当频差变化率越过设定值时，控制电池储能以额定功率输出，当频率开始恢复时变换至下垂控制（单位调节功率系数（即下垂系数的倒数）为经验值）。现有研究对储能参与调频展开了初步探索，并没有从机理层面分析如何参与，因此无法充分利用其容量。一般来说，传统的快速调频过程包含两个环节，1）惯性控制；2）一次调频（下垂控制），负荷的频率调节效应也可纳入此环节。显然，在快速调频场景下引入储能并展开容量配置研究很有必要。

提出一种考虑储能参与快速调频动作时机与深度的容量配置方法。基于快速调频评估指标，利用复频域灵敏度原理分析了含储能的区域电网频率特性，提出了储能的综合控制模式；依据时域灵敏度原理推导了储能参与快速调频时的时域频率响应特性，并给出了相关动作时机及其应当采取的控制模式，同时结合调频评估指标要求确定了所必需的动作深度，进而形成了储能容量配置方法并给出了相应的流程；最后进行仿真验证并展望。

2 相关概念以及调频评估指标

储能参与快速调频的关键在于控制指令的计算，与此相关的概念包括控制模式、动作时机与深度。控制模式为其参与快速调频的方式；动作时机为其参与快速调频的初始投入、控制模式切换、退出以及为维持荷电状态（State Of Charge，SOC）在设定的参考值SOCref的额外充放电等运行状态对应的时刻；动作深度为其参与快速调频时的出力大小。

快速调频过程的评估指标与频率、调频电源相关[8]，如下:1）ΔpL(t)、Δf(t)和Δo(t)分别为负荷扰动、频率偏差和频差变化率，Δo0、Δfm、Δfs、t0、tm和ts分别为初始频差变化率、最大频率偏差、稳态频率偏差、扰动起始时间、峰值时间（即Δo(t)第一次过零的时刻）和调节时间（即Δf(t)到达并保持在Δfs值±2%误差范围内所需的最短时间[9]），t0和Δf(t0)一般均为0；Δfdb为一次调频死区；Δomax、Δfm_max、Δfs_max和Δfdb_max是在确定电网条件下的调频评估指标要求，分别为频差变化率限值、最大频率偏差限值、稳态频率偏差限值和一次调频死区限值。2）Gpm和Gps分别为各调频电源的短时贡献电量和长时贡献电量，可以分别通过对其在t0～tm、t0～ts时段内的动作深度进行积分得到。其中，1）中指标可以反应扰动大小和频率变化情况，并能为继电保护动作提供正确的触发信号。2）中指标可以反应调频电源对电网的有功支援情况。

时域中的ΔpL(t)、Δf(t)和Δo(t)分别对应复频域中的ΔPL(s)、ΔF(s)和ΔO(s)。由定义可知ΔO(s)=s·ΔF(s)，在此假设ΔF(s)与ΔPL(s)之比为TESS(s)，ΔO(s)与ΔPL(s)之比为T'ESS(s)。为分析区域电网对参数变化的敏感程度，引入绝对灵敏度（下文称为灵敏度系数）；同时，为比较分析不同参数的相对变化对区域电网的影响，引入相对灵敏度（即对灵敏度系数做归一化处理，下文称为灵敏度）[10]。对于区域电网，一般基于阶跃负荷扰动展开分析，即取ΔPL(s)为ΔpL/s，ΔpL为标幺值。

3 含储能的区域电网频率特性

3.1虚拟惯性控制

面向快速调频应用，储能采用虚拟惯性控制模式时的区域电网等效模型如图1所示。

图1 含储能的区域电网等效模型（虚拟惯性控制）Fig.1 Regional power grid equivalent model involving ESS (virtual inertial control)

列写图1中的传递函数方程，可得

式（1）～式（3）为复频域中的方程，其描述了含储能的区域电网的基本特性。式（1）中，ΔPG(s)为传统调频电源的动作深度；KG和G(s)分别为传统调频电源的单位调节功率系数和传递函数模型；ΔPE(s)为储能的动作深度；ME和N(s)分别为储能的虚拟惯性系数和传递函数模型。式（2）中，M和D分别为电网的惯性时间常数和负荷阻尼系数。式（3）中，TG、TCH、TRH和FHP分别为传统调频电源的调速器时间常数、汽轮机时间常数、再热器时间常数和再热器增益，对应值为0.08、0.3、10秒和0.5[1]。

如果要准确的对储能进行分析和计算，必须构建出适合快速调频研究需求的仿真模型，限于篇幅，建模部分的内容已在另文详述。为便于研究，本文假设[11-12]

式中，TPCS为功率转换系统（Power Control System，PCS）的时间常数。

结合式（1）和式（2），可得

由上式可得

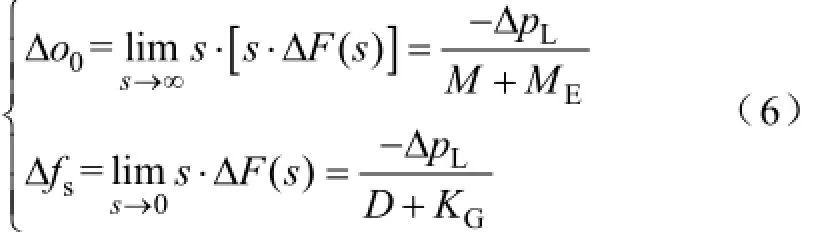
由式（5）和式（6）可知，当ΔPL(s)为正值时，|ΔF(s)|(即ΔF(s)的绝对值)的变化速率取决于M和ME，且Δo0值为(-ΔpL)/(M+ME)。当|ΔF(s)|上升，传统调频电源和储能的动作深度会增加，这反过来引起了|ΔF(s)|上升速率的减少，并在传统调频电源和储能的动作深度之和超过ΔPL(s)时开始恢复|ΔF(s)|。这个|ΔF(s)|最终稳定于Δfs，显然该值与ME无关，此时传统调频电源的动作深度等于ΔPL(s)，储能的动作深度为0。显然此控制模式能够快速抑制ΔO(s)，但对Δfs无改善作用。ΔPL(s)为负值时的ΔF(s)变化过程类似，此处不累述。

基于式（5），可得

结合式（5）和式（7），分析可得ΔF(s)和ΔO(s)对ME的灵敏度系数和灵敏度分别为

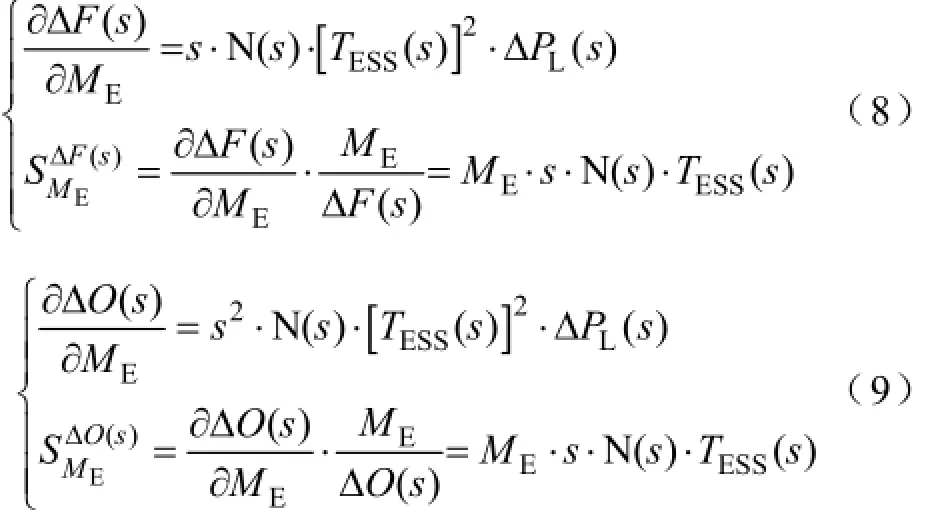
同理得TESS(s)和T'ESS(s)对ME的灵敏度为

结合式（8）～式（10）可知，ΔF(s)、ΔO(s)、TESS(s)和T'ESS(s)对ME的灵敏度相同，进而可知此控制模式下的灵敏度与ΔPL(s)无关。进一步推导得到灵敏度的初始值（Original Value，OV）和稳态值（Steady State Value，SS）为

由上式可知，灵敏度的初始值为与M和ME相关的负数，而稳态值为0，因此能得到与式（5）和式（6）相同的分析结果。

假设KG、M和D分别为23.34 p.u.MW/p.u.Hz、7 s和1 p.u.MW/p.u.Hz，当ME分别取为3和4 p.u.MW·s/p.u.Hz时，可得对应的灵敏度曲线如图2所示。图中，灵敏度由负值变为正值后趋于稳态值0，其为负值表示增加ME会促进ΔF(s)的恢复，为正值表示增加ME会阻碍ΔF(s)的恢复，为0表示ME对ΔF(s)不起作用；ME从3增加至4时，灵敏度的绝对值会增大，进而表明其在过零之前（即为负值），ME的增加会增强对ΔF(s)的改善作用，而过零之后ME的增加反而会加剧阻碍ΔF(s)的恢复；灵敏度的初始值的绝对值最大且稳态值为0，表明储能在扰动初期所起的作用较大，而在稳态时不起作用。

3.2虚拟下垂控制

储能采用虚拟下垂控制模式时的区域电网等效模型如图3所示。

图3 含储能的区域电网等效模型（虚拟下垂控制）Fig.3 Regional power grid equivalent model involving ESS (virtual droop control)

图中KE为储能的虚拟单位调节功率系数；其余参数的含义同图1。此时

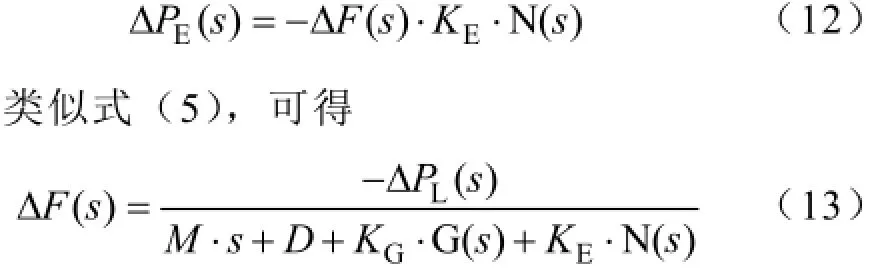
同理，由上式可得

由式（13）和式（14）可知，当ΔPL(s)为正值时，|ΔF(s)|会按一定的速率增大，Δo0值为(-ΔpL)/M，即其仅取决于M。当储能和传统调频电源的动作深度之和超过ΔPL(s)时，|ΔF(s)|开始减小并最终稳定于Δfs，此时两者的动作深度之和与ΔPL(s)相等。显然此控制模式能够有效改善Δfs，但对Δo0不起作用。ΔPL(s)为负值时的ΔF(s)变化过程类似，在此不累述。

基于式（13），可得

结合式（13）和式（15），分析可得ΔF(s)和ΔO(s)对ME的灵敏度系数和灵敏度分别为

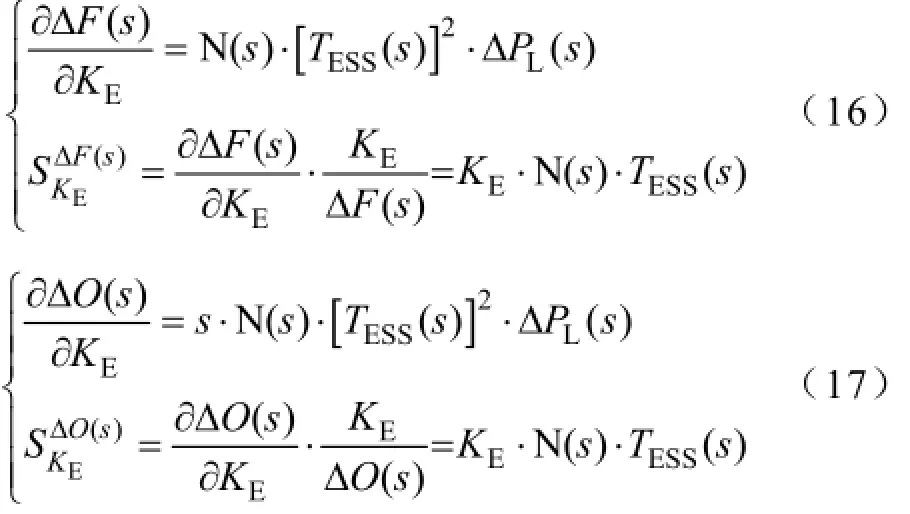
同理得TESS(s)和T'ESS(s)对KE的灵敏度为

结合式（16）～（18）可知，ΔF(s)、ΔO(s)、TESS(s)和T'ESS(s)对KE的灵敏度相同，进而可知此控制模式下的灵敏度也与ΔPL(s)无关。进一步推导得到灵敏度的初始值和稳态值分别为

由上式可知，灵敏度的初始值为0，而其稳态值为与D、KG和KE相关的负数，因此能得到与式（13）和式（14）相同的分析结果。

同理，当KE分别取为3和4 p.u.MW/p.u.Hz时，可得对应的灵敏度曲线如图4所示。图中，灵敏度恒为负值（t0时刻除外），其绝对值在快速达至最大后缓慢减小并趋向稳态值，即储能在运行过程中保持对ΔF(s)的改善作用；KE从3增加至4时，灵敏度的绝对值明显增大，进而表明KE的增加会增强储能对ΔF(s)的改善作用；灵敏度的初始值为0且稳定于某确定值，这表明储能在扰动后期所起的改善作用较大。

图4 虚拟下垂控制模式下的灵敏度曲线Fig.4 Sensitivity curve under virtual droop control

3.3储能的综合控制模式

综上，虚拟惯性和虚拟下垂控制模式时的储能均能对ΔF(s)起到一定的改善作用，且各灵敏度均与ΔPL(s)无关。前者充分利用了储能的快速响应特性，对Δo0的改善效果显著，而对Δfs不起作用，由于灵敏度存在过零点，过零前其对ΔF(s)的改善作用更为显著，但过零后对ΔF(s)的阻碍作用也更为明显。后者中储能对Δo0不起作用，但对Δfs的改善效果显著，由于灵敏度恒为负值，则其对ΔF(s)的改善作用较为持续。

因此，为充分利用储能的技术优势和改善电网调频效果，针对其提出一种包含虚拟惯性和虚拟下垂的综合控制模式。下文将介绍考虑储能动作时机与深度的容量配置方法。

4 考虑动作时机与深度的容量配置方法

在时域中，通过分析灵敏度系数的特征，确定储能的动作时机及其应当采取的控制模式，基于此将快速调频过程划分为不同的时段，并结合调频评估指标要求得到各时段的动作深度，进而形成储能的容量配置方法。

4.1基于时域灵敏度系数分析的动作时机

由于储能的响应时间远小于传统调频电源，因此在研究过程中可近似认为TPCS为0[13]，即N(s)近似等于1，基于此前提展开分析。

4.1.1 灵敏度系数的特征分析

研究虚拟惯性控制模式下Δo(t)对ME的灵敏度系数绝对值最大时对应的时刻与t0之间的关系，Δf(t)对ME的灵敏度系数绝对值最小时对应的时刻与tm之间的关系；虚拟下垂控制模式下Δf(t)对KE的灵敏度系数绝对值最大时对应的时刻与tm之间的关系。

1）Δo(t)对ME的灵敏度系数

Δo(t)对ME的灵敏度系数最大时对应的时刻即为其一阶导数为零的时刻，结合式（9），可得

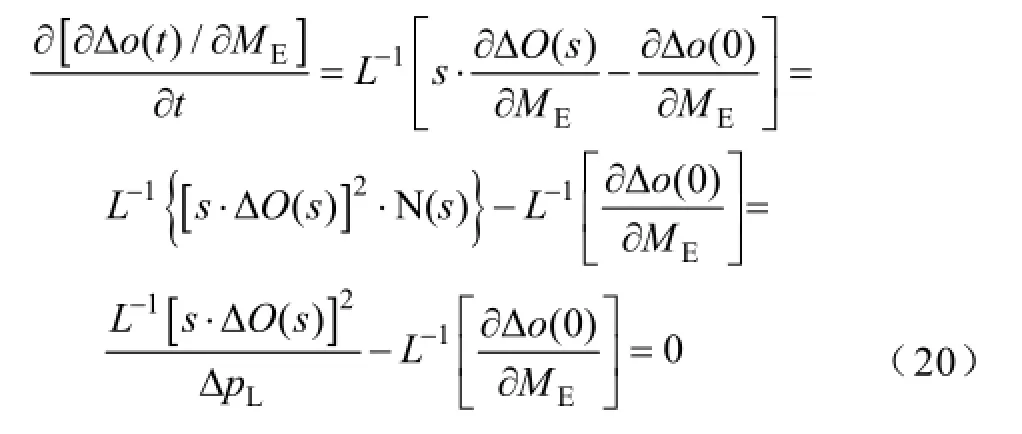
对于任意复频域函数G1(s)和相应的时域函数g1(t)，有假设G1(s)=[ΔO(s)]2，则可得由上式可知:

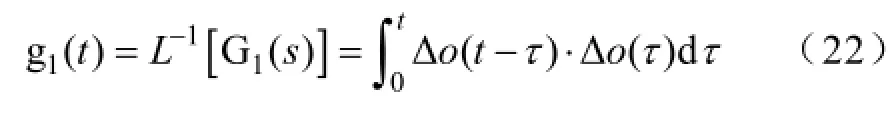
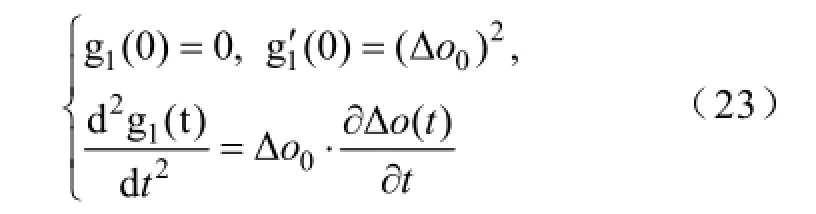
Δo(t)对ME的灵敏度系数在t0时刻的值为

由前文的式（6）可知Δo0为(-ΔpL)/(M+ME)。因此，结合式（20）～式（24），可得

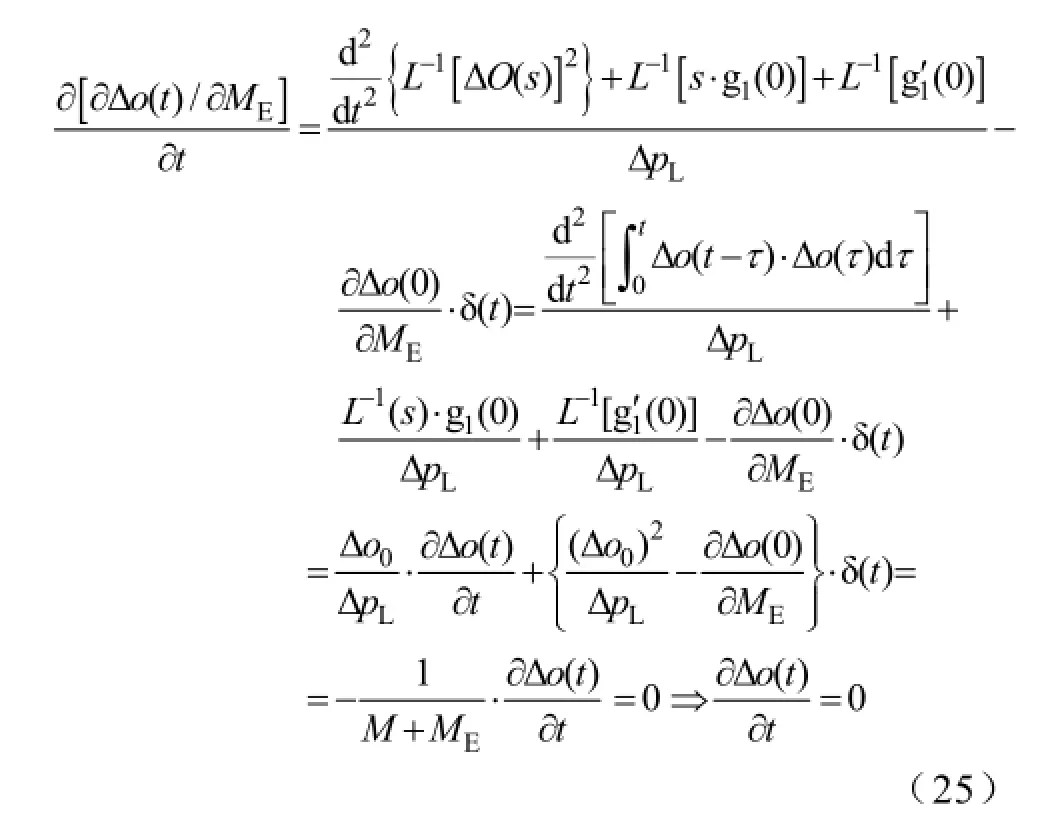
式中，δ(t)为单位冲激函数。

由上式可知，Δo(t)对ME的灵敏度系数的一阶导数为零的时刻与∂Δo(t)/∂t=0对应的时刻相同。

在0～tm时段，当ΔpL为正值时，显然Δo(tm)=0、Δo0为负值且Δo(t)单调上升，进而可知∂Δo(t)/∂t为正值且Δo(t)对ME的灵敏度系数的一阶导数为负值，即Δo(t)对ME的灵敏度系数单调下降，则其最大值为式（24）所示t0时刻的值(Δo0)2/ΔpL；当ΔpL为负值时，可知Δo(t)对ME的灵敏度系数的负向最大值也为(Δo0)2/ΔpL。结合可得Δo(t)对ME的灵敏度系数绝对值最大时对应的时刻为t0。

2）Δf(t)对KE的灵敏度系数

Δf(t)对KE的灵敏度系数最大时对应的时刻即为其一阶导数为零的时刻[10]，结合式（16），可得其一阶导数为

假设同样满足式（21）的G2(s)等于[ΔF(s)]2，可得对应的时域函数

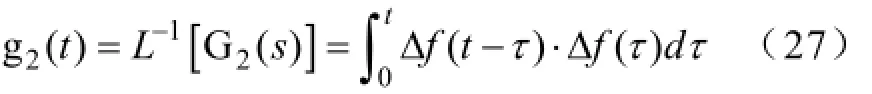
由上式可知:

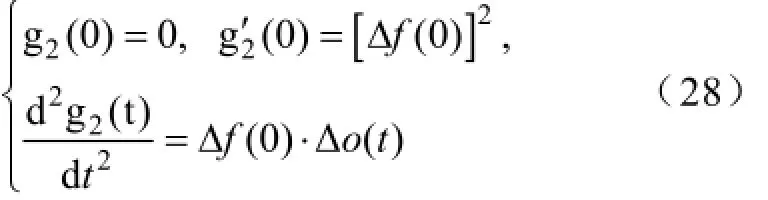
推得Δf(t)对KE的灵敏度系数在t0刻的值为结合式（21）和式（26）～式（29），可得

由上式可知，Δf(t)对KE的灵敏度系数一阶导数为零的时刻与Δo(t)=0对应的时刻相同。

在0～tm时段，当ΔpL为正值时，由前述分析可知Δo(t)由负向最大值单调上升至0，进而可知Δo(t)对ME的灵敏度系数的一阶导数为负值，即Δo(t)对ME的灵敏度系数单调下降；同时，式（24）显示其在t0时刻的值为0，则可知Δf(t)对KE的灵敏度负向最大值对应的时刻为tm。同理，当ΔpL为负值时，Δo(t)对ME的灵敏度系数的正向最大值对应的时刻也为tm。结合可得Δo(t)对ME的灵敏度系数绝对值最大时对应的时刻为tm。

3）Δf(t)对ME的灵敏度系数

结合式（8），经推导可得Δf(t)对ME的灵敏度系数为零时对应的表达式为

上式显示的结果与式（26）相同，进而可知Δf(t)对ME的灵敏度系数绝对值最小时对应的时刻为tm。综上可知:在t0时刻，Δo(t)对ME的灵敏度系数的绝对值最大；在tm时刻，Δf(t)对KE的灵敏度系数的绝对值最大且Δf(t)对ME的灵敏度系数的绝对值最小。

4.1.2 动作时机以及对应的控制模式

基于前述分析，可得储能的各动作时机所对应的运行状态应当分别满足下述条件:

1）在t0时刻，Δo(t)对ME的灵敏度系数绝对值最大且此时的Δo(t)的绝对值最大，随后频率会快速下滑。因此，为较好的满足Δo0和Δfm的控制要求，以t0时刻作为储能参与快速调频的初始投入时机，同时选用虚拟惯性控制模式。

2）在tm时刻，Δf(t)对KE的灵敏度系数绝对值最大、Δf(t)对ME的灵敏度系数绝对值最小且|Δf(t)|为最大值，随后频率会逐步恢复。因此，为较好的

步骤1，首先获取区域电网的基础参数；然后统计典型工况（非峰荷期和峰荷期等）下的最大过剩功率（需要储能充电）ΔPmaxsurplus和最大缺额功率（需要储能放电）ΔPmaxshortage，则对应工况下的最大负荷扰动ΔpL_max为max(ΔPmaxsurplus, ΔPmaxshortage)，此时需要提出各工况下的调频评估指标要求。

步骤2，基于步骤1，首先利用灵敏度原理确定储能的初始投入时机，同时选用虚拟惯性控制模式，并依据式（34）确定此调频时段对应的ME与所需的PE1之间的关系；其次确定储能的控制模式切换时机，同时选用虚拟下垂控制模式，并依据式（35）确定此调频时段对应的KE与所需的PE2之间的关系。最后利用式（36）确定储能的PE，进而得到ME和KE的值。

步骤3，设置储能的容量为E(k)，SOCref取为0.5。基于步骤1确定的ΔpL_max和步骤2确定的PE、ME和KE，仿真模拟对应工况下的充电或放电情况。记录t0～tm时段内第i时刻的动作深度ΔPE_i，Δfm对应的时间tm，tm～ts时段内第j时刻的动作深度ΔPE_j，Δfs对应的时间ts。评估设置的储能容量能否满足快速调频要求，如果满足则结束此过程，此时额定容量EB取为所设置的容量值E(k)，否则增加或减少设置的容量值，然后继续执行步骤4。

步骤4，设置k=k+1，定义储能的容量增量为ΔE(k)，此时对应的容量E(k)=E(k-1)+ΔE(k)，继续返回执行步骤3。

5 仿真验证与讨论

以某典型电网的参考事故和调频评估指标要求为初始条件[7-8]展开仿真研究，数据如表1。表中工况1为非峰荷期，SBASE为150 MW；工况2为峰荷期，SBASE为250 MW；其余参数均为标幺值，它们均以对应工况下的SBASE和额定频率50 Hz为基准。

表1 电网参考事故和调频评估指标要求Tab.1 Power grid reference accidents and frequency regulation evaluation index requirements

5.1灵敏度系数分析结果的仿真验证

利用表1中的工况1验证前述式（25）、式（30）和式（31）所示灵敏度系数方程的正确性，可得两种控制模式下的仿真结果分别如图6和图7所示。

图6 虚拟惯性控制模式下的灵敏度系数曲线Fig.6 Sensitivity coefficient under virtual inertial control

图7 虚拟下垂控制模式下的灵敏度系数曲线Fig.7 Sensitivity coefficient under virtual droop control

由图6a可知，在t0时刻，Δo(t)对ME的灵敏度系数绝对值最大且Δo(t)的绝对值也最大；由图6b可知，在tm时刻，Δf(t)对ME的灵敏度系数绝对值最小(即为0)且|Δf(t)|为最大值，随后灵敏度系数过零点进而阻碍Δf(t)恢复。由图7可知，Δf(t)对KE的灵敏度系数绝对值最大且|Δf(t)|也为最大值。仿真结果验证了前述理论推导的正确性。

5.2功率和容量需求的分析以及仿真验证

5.2.1 功率需求分析及仿真验证

假设负荷扰动与M、D无关，基于此前提，对表1所述两种工况下储能的功率需求进行分析。对工况1，若需控制Δo0≥ Δomax，PE0需满足如下要求: 4.8MW ≤ PE0≤ 30MW；若需控制Δfm≥ Δfm_max，M1应取为10.8 s，从而可得PE1≥ 11.4 MW；若需控制Δfs≥ Δfs_max，可得PE2≥ 10.344 MW。同理，对于工况2，可得3 MW ≤ PE0≤ 30 MW，M1应取为11.4 s，PE1≥ 7.8 MW，PE≥ 9.75 MW。综合可得功率配置结果如表2所示。

表2 储能的功率配置结果Tab.2 Allocation results of ESS power

由表可知，两种工况下所需的储能功率分别为11.4和9.75 MW，考虑到储能的效率，建议选取额定功率为12 MW。基于此，以对应工况下的SBASE为基准，可得ME和KE在工况1中的取值分别为3.8和3.45，在工况2中的取值分别为2.4和3。基于该功率配置展开仿真实验，对比仅含传统调频电源（Traditional Frequency Regulation，TFR）调频和传统调频电源与储能（TFR-ESS）联合调频两种方案，结果如图8、图9和表3所示。图中传统调频电源和储能的动作深度均以对应工况下的SBASE为基准。

图8 电网引入储能前后的调频结果（工况1）Fig.8 Frequency regulation results before and after the introduction of ESS (operating mode 1)

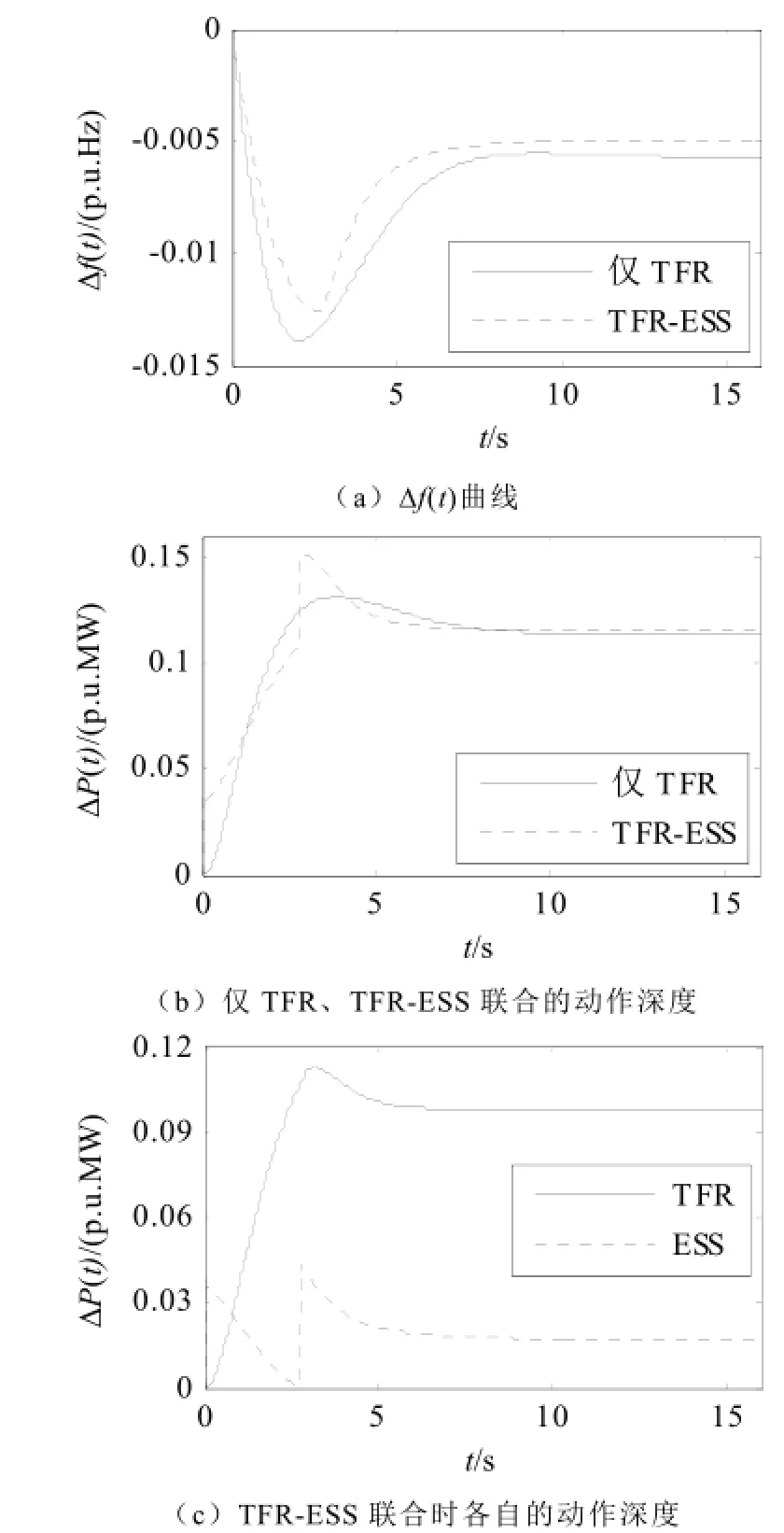
图9 电网引入储能前后的调频结果（工况2）Fig.9 Frequency regulation results before and after the introduction of ESS (operating mode 2)

对于这两种工况，图8a和图9a为Δf(t)曲线，结合下表3中的Δo0、Δfm和Δfs指标可知，储能的引入显著改善了调频效果，且两种工况下的调频评估指标计算结果均能较好的与理论分析相吻合，即达到了参考事故下的频率控制要求，其中工况1的Δo0从-0.0286变为-0.0186 p.u.Hz/s，工况2的Δo0从-0.0134变为-0.01 p.u.Hz/s，满足了表1所述的Δomax要求，同时，Δfm和Δfs指标也满足相应的Δfm_max和Δfs_max要求。图8b和图9b为仅TFR和TFR-ESS联合调频的动作深度，结合表中的Gpm和Gps指标可知:相比仅TFR调频，TFR-ESS联合调频的优势在于t0～tm时段的Gpm上，而在Gps上差距较小，这表明储能的引入在改善调频效果的同时，并未增加太多额外的调频电量需求。图8c和图9c为TFR-ESS联合调频时传统调频电源和储能各自的动作深度，由图可知，相比仅TFR调频，此时传统调频电源的动作深度相对减小，即引入储能可减轻它的调频负担；同时，理论分析得出的12MW储能可较好的满足各工况需求，其最关键的作用是在扰动瞬间提供了峰值功率，避免了Δo0的突变及低频减载的启动，并将Δfs控制在要求范围内。

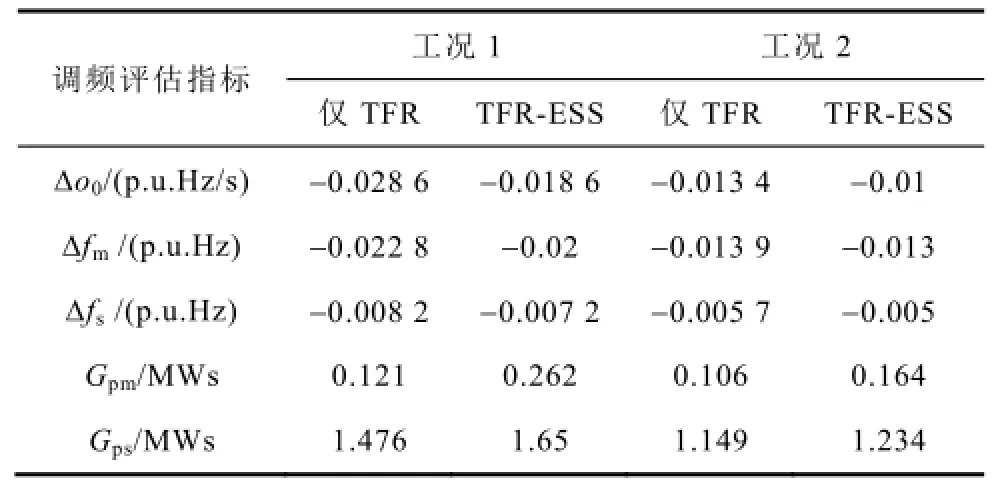
表3 调频评估指标计算结果Tab.3 Calculation results of frequency regulation evaluation indices

5.2.3 容量需求的分析

通过对储能在各调频时段内的动作深度进行积分，可得到两种工况下的容量配置结果（包含额定功率与持续时间）如表4所示。

表4 储能的容量配置结果Tab.4 Allocation results of ESS capacity

由表可知，在对应时段选择两种工况下所配置容量的较大值，即在t0～tm时段内配置12MW-1s、在t0～ts时段内配置12MW-4.3s就能满足调频要求。为了避免储能的深度充放电而影响其使用寿命，且保持其在下一调频任务时处于可充和可放的状态（即控制SOC接近于SOCref，一般取SOCref为0.5）并计及PCS的损耗，建议最终选取储能的容量配置方案为12MW-9s。

5.2.3 讨论

本文方法考虑了储能参与快速调频的动作时机与深度，在t0～tm时段采用虚拟惯性控制模式，通过此模式能够较大程度地减小|Δo0|和|Δfm|值，相比已有方法中直接控制储能以最大需求进行恒功率充电或者放电的方式，其能显著降低此调频时段对储能的容量需求；同时，以tm作为运行模式的切换时机，在tm～ts时段采用虚拟下垂控制模式，通过此模式能够显著减小|Δfs|值。因此，在较少的储能容量配置前提下，不仅能更好的满足调频评估指标要求，还能避免由于Δo(t)和Δf(t)越限所引发的减载或者切机等问题。

由于储能的快速响应特性导致其比传统调频电源高效，其引入也间接减少了传统调频电源的容量需求，而节省的容量可用于电网的调峰和事故备用等，从而进一步提高了电网运行的安全性与可靠性。应当指出，阶跃输入对于电网而言是最严峻的工作状态，如果在此扰动下电网的性能指标能满足要求，那么其他形式的扰动作用（如连续小负荷扰动）下电网动态性能也同样能达到要求[9]，因此前述仿真研究能说明所提容量配置方法的合理性。

6 结论

1）提出的将惯性控制和下垂控制相结合的综合控制模式能充分利用各控制模式的优势，即惯性控制对功率扰动初期的频差变化率和最大频率偏差、下垂控制对稳态频率偏差各有显著的改善作用。

2）根据频率特性分析得到的确定合理动作时机的必要条件，及结合此条件给出的参与快速调频的相关动作时机及控制模式，可为优化储能运行提供参考。

3）仿真表明，依据本文容量配置方法所得的储能功率和容量配置方案，在同样的功率扰动下，能有效改善调频评估指标；在同样的调频评估指标要求下，可减少最大功率和容量需求，特别是对容量需求的降低效果明显。

未来需进一步研究储能参与快速调频的经济价值评估问题。

[1] Kundur P. 电力系统稳定与控制[M]. 北京： 中国电力出版社, 2002： 389-410.

[2] Ulbig A, Borsche T S, Andersson G. Impact of low rotational inertia on power system stability and operation[C]. IFAC World Congress 2014, Capetown, South Africa, 2014： 1-12.

[3] 刘世林, 文劲宇, 孙海顺, 等. 风电并网中的储能技术研究进展[J]. 电力系统保护与控制, 2013, 41(23)： 145-153.

Liu Shilin, Wen Jinyu, Sun Haishun. Progress on applications of energy storage technology in wind power integrated to the grid[J]. Power System Protection and Control, 2013, 41(23)： 145-153.

[4] 熊雄, 杨仁刚, 叶林, 等. 电力需求侧大规模储能系统经济性评估[J]. 电工技术学报, 2013, 28(9)：224-230.

Xiong Xiong,Yang Rengang,Ye Lin, et al. Economic evaluation of large-scale energy storage allocation in power demand side[J].Transactions of China Electrotechnical Society, 2013, 28(9)： 224-230.

[5] Goikoetxea A, Barrena J A, Rodriguez M A, et al. Frequency restoration in insular grids using Ultracaps ESS[C]. International Symposium on Power Electronics Electrical Drives Automation and Motion(SPEEDAM), Pisa, Italy, 2010： 1280-1285.

[6] Aghamohammadi M R, Abdolahinia H. A new approach for optimal sizing of battery energy system for primary frequency control of islanded Microgrid [J]. Electrical Power and Energy Systems, 2014, 54：325-333.

[7] Delille G, Francois B, Malarange G. Dynamic frequency control support by energy storage to reduce the impact of wind and solar generation on isolated power system’s inertia[J]. IEEE Transactions on Sustainable Energy, 2012, 3(4)： 931-939.

[8] DÍaz-González F, Hau M, Sumper A, et al. Participation of wind power plants in system frequency control： Review of grid code requirements and control methods [J]. Renewable and Sustainable Energy Reviews, 2014, 34： 551-564.

[9] 胡寿松. 自动控制原理第五版[M]. 北京： 科学出版社, 2007： 71-73.

[10] Huang Hao, Li Fangxing. Sensitivity analysis of loaddamping characteristic in power system frequency regulation[J]. IEEE Transactions on Power System, 2013, 28(2)： 1324-1335.

[11] 李妍, 荆盼盼, 王丽, 等. 通用储能电源数学模型及其PSASP建模研究[J]. 电网技术, 2012, 36(1)： 51-57.

Li Yan, Jing Panpan, Wang Li, et al. A mathematical model of versatile energy storage system and its modeling by power system analysis software package [J]. Power System Technology, 2012, 36(1)： 51-57.

[12] 陆秋瑜, 胡伟, 郑乐, 等. 多时间尺度的电池储能系统建模及分析应用[J]. 中国电机工程学报, 2013, 33(16)： 86-93.

Lu Qiuyu, Hu Wei, Zheng Le et al. Modeling and analysis of battery energy storage systems in multitime scales application[J]. Proceedings of the CSEE, 2013, 33(16)： 86-93.

[13] 娄素华, 易林, 吴耀武, 等. 基于可变寿命模型的电池储能容量优化配置[J]. 电工技术学报, 2015, 30(4)： 265-271.

Lou Suhua, Yi Lin, Wu Yaowu, et al. Optimizing deployment of battery energy storage based on lifetime predication[J].Transactions of China Electrotechnical Society, 2015, 30(4)： 265-271.

3）在ts时刻，Δf(t)稳定于Δfs且Δo(t)恒为0，快速调频过程结束。因此，以ts时刻作为储能参与快速调频的退出时机。

4）快速调频过程结束后需维持储能SOC接近于SOCref，从而能更好的迎接下一次调频任务，因此需对其进行额外的充放电，确定此时机的方法可参阅文献[8]。

综合以上四点则完成了储能参与快速调频的动作时机确定。因此，可将快速调频过程划分为如下两个时段，第一时段为t0～tm，对应采用虚拟惯性控制模式；第二时段为tm～ts，对应采用虚拟下垂控制模式。下节将分析各调频时段所必需的动作深度。

4.2基于调频评估指标要求的动作深度

假设储能放电为正，充电为负。假设ΔpL为正值，分析各调频时段储能所必需的动作深度。

1）t0时刻储能的动作深度分析

引入功率变量PE0。t0时刻需满足Δomax≤ Δo0≤0，假设储能的动作深度为ΔPE0，此时可得

一般选择上式中的较小值作为ΔPE0的值，即取为(ΔpL+M·Δomax)，从而可得PE0如下式:式中，SBASE为电网的额定容量。

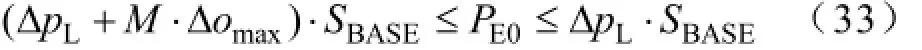
针对具体的电网需求，PE0值可在此范围内灵活选择，一般取较小值。

2）t0～tm时段内储能的动作深度分析

引入功率变量PE1。该时段储能通过虚拟惯性控制模式参与快速调频，对应的ME确定方法如下:利用参数轨迹灵敏度方法[9]分析M对Δfm的影响，为实现Δfm≥Δfm_max的目标，能分析出合适的惯性时间常数M1，进而可知ME需满足

3）tm～ts时段内储能的动作深度分析

引入功率变量PE2。该时段储能通过虚拟下垂控制模式参与快速调频，当快速调频过程结束，即Δf(t)达至Δfs时，经推导可得KE需满足

由式（34）和式（35）可知，只要选定SBASE、ΔpL、Δfs_max、KG、D、PE1和PE2，即可确定ME和KE。对于确定的电网，ΔpL能通过统计确定，SBASE、Δfs_max、KG和D也为已知量，因此ME的选取仅与PE1相关，KE的选取仅与PE2相关。一般通过以上两式首先确定PE1与PE2的值，PE0取式（33）中的(ΔPL+M·Δomax)·SBASE，从而可得储能的额定功率PE满足

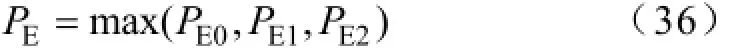
通过PE可最终确定ME与KE的值，从而完成储能参与快速调频的动作深度确定。

4.3容量配置方法

基于前述工作，形成考虑储能的容量配置流程如图5所示。过程如下:

Capacity Allocation of Energy Storage System Considering Its Action Moment and Output Depth in Rapid Frequency Regulation

Huang Jiyuan Li Xinran Cao Yijia Liu Weijian
（College of Electrical & Information Engineering, Hunan University Changsha 410082 China）

An energy storage system (ESS) capacity allocation method considering its action moments and depth in rapid frequency regulation (RFR) is proposed in this paper. Firstly, frequency characteristics of regional power grids involving ESS were analyzed with sensitivity theory on complex frequency domain. Based on it, a comprehensive control mode composed of virtual inertial control and virtual droop control was proposed for ESS. Then, based on sensitivity theory on time domain and frequency regulation evaluation indices, the frequency response characteristics on time domain of ESS in RFR were derived in theory, the conditions to determine the reasonable action moments for ESS were analyzed, and the relative action moments and adopted control modes were presented according to these conditions; meanwhile, in accordance with the requirements of frequency regulation evaluation indices, the action depth was determined and its relationship with the rated power was derived, thus forming the capacity allocation method of ESS and putting forward its process. Finally, simulations ran with reference accidents of a typical grid as their initial conditions. The results show that the proposed method can satisfy the requirements of frequency regulation evaluation indices with a small ESS capacity.

Energy storage, rapid frequency regulation, action moment, action depth, capacity allocation

图5 容量配置流程Fig.5 Capacity allocation process

TM732

黄际元 男，1988年生，博士研究生，研究方向为储能在电网中的应用及建模。

李欣然 男，1957年生，教授，博士生导师，研究方向为电力系统分析控制、负荷建模。满足Δfs的控制要求，以tm时刻作为储能控制模式切换时机，由虚拟惯性控制模式切换为虚拟下垂控制模式。

国家重点基础研究发展计划（973计划）（2012CB215106），国家自然科学基金项目（51477043）。

2014-09-10