电力系统主动解列的可行解列时窗研究

丁 磊 郭一忱 陈 青 Vladimir Terzija,

电力系统主动解列的可行解列时窗研究

丁 磊1郭一忱1陈 青1Vladimir Terzija1,2

（1. 电网智能化调度与控制教育部重点实验室(山东大学) 济南 250061 2. The University of Manchester, Manchester, UK, M13 9PL）

解列时刻是决定解列是否成功的关键因素。常规解列研究基于解列前的静态潮流信息，对动态过程中的稳定性问题利用强假设进行规避，忽略解列时刻的研究。本文首次对主动解列的解列时刻问题展开系统性分析，利用暂态能量函数量化解列动态过程中孤岛的稳定性，利用孤岛失稳的临界能量确定暂态稳定意义下的可行解列时窗，以保证解列后孤岛的暂态稳定性。研究表明，因扰动背景不同，孤岛的可行解列时窗呈现出：任何时刻均可解列、小于某个临界时刻、大于某个临界时刻、呈现断续的时窗特征以及可行解列时窗为空等五种不同的情况。本文首次从机理上解释和刻画主动解列的解列时刻特征，为进一步研究主动解列问题提供了新的思路和支撑。

主动解列 可行解列时窗 稳定域 暂态能量函数

1 引言

主动解列（Controlled islanding）是指为有效避免和限制大停电的发生，利用广域测量系统WAMS（Wide Area Measurement System）在线获取系统实时信息，在电网受到严重扰动、无法继续完整运行时，将系统解列为多个稳定运行的孤岛的控制方式。一个完整的解列策略应当包括:判断是否解列、确定解列断面以及确定解列时刻。

“判断是否解列”即系统故障后的暂态稳定评估问题这一传统课题已经有较多的研究。文献[1]提出利用决策树和动态安全评估对系统进行解列前的暂态稳定评估。文献[2,3]提出利用OMIB（单机无穷大母线）模型和EEAC（扩展等面积法则）来判断是否需要解列并识别机组分群。

目前对主动解列的研究主要侧重于“确定解列断面”这一问题。文献[4-9]分别提出了OBDD法（二元有序决策图）、弱连接法、谱聚类法、启发式搜索算法和混合整数规划等方法对解列断面的选取进行建模求解。这些方法大多基于解列前的静态潮流信息，仅考虑孤岛内的发电机需要保持同调和孤岛内有功功率近似平衡这些稳态和准稳态的约束条件，对动态过程中的稳定问题则利用强假设（假设同调机群在解列过程中不会失稳以及解列后的孤岛能够稳定运行）进行规避。

在判断出需要解列并确定解列断面以后，解列的操作时刻将成为解列是否成功的关键因素。如果在正确的时刻进行解列，可以平稳过渡到稳定的孤岛运行；如果错过了正确的解列时刻，解列后孤岛无法稳定运行，会造成解列失败和系统崩溃。

由于常规解列研究对解列动态过程中的稳定问题做了强假设，假设同调机群在解列过程中不会失稳，解列时刻问题一直没有得到充分研究。文献[10]从解列后子系统积聚动能大小的角度分析系统的解列时刻，认为解列时刻应采取尽可能快的原则才更有利于故障后子系统暂态稳定的恢复。该文献是目前能检索到的研究解列操作时刻的少数文献之一，但其出发点仍然是先假定孤岛内的发电机群强同调，再从减小孤岛等值发电机积聚动能的角度考虑解列时刻，并没有考虑解列过程中孤岛内部发电机同步性对解列时刻的要求。

本文首次对主动解列的解列时刻展开系统性分析，把主动解列时刻的确定划分为两个阶段。第一阶段，从暂态稳定和稳定域的角度对解列时刻进行解释和分析，研究解列过程中孤岛内部发电机同步性对解列时刻的要求；通过能量函数法对给定扰动事件背景和解列策略的系统进行量化分析，刻画单个孤岛和整个系统的可行解列时窗的分布特征。第二阶段，在保证孤岛内部同调性和稳定性的基础上，考虑孤岛惯量中心的频率偏移，对可行解列时窗进一步修正。本文的研究重点是第一阶段，即确定暂态稳定意义下的可行解列时窗。

2 稳定性和暂态能量函数

2.1稳定和稳定域定义

自治非线性动力系统的动力微分方程可以表示为x˙=f[x(t)]，x∈Rn，t0时刻从x0= x(t0)开始的系统轨迹记作φ(x,t)，系统的平衡点定义为xˆ∈f(xˆ)= 0[11]。

李雅普诺夫稳定:对t≥t0，若任意ˆx∈Rn的邻域U，都存在一个ˆx的邻域V，使从邻域V中任意一点出发的系统轨迹φ(x,t)∈U，则称ˆx是稳定的。

渐进稳定:对t≥t0，存在ˆx∈Rn的邻域U，使从邻域U中任意一点出发的系统轨迹φ(x,t)∈U且趋近于ˆx，则称ˆx是渐进稳定的。

稳定域:稳定平衡点（Stable Equilibrium Point, SEP）xs的稳定域（或吸引域）A(xs) 定义为所有满足limt→∞φ(x,t)→xs的x点的集合，其边界定义为稳定边界s()Ax∂。

2.2暂态能量函数和主导UEP

电力系统经受大扰动后的暂态稳定性可以通过时域仿真、扩展等面积法则和暂态能量函数法等方法进行评估。基于暂态能量函数法的暂态稳定性评估包括以下步骤[11]:

1. 构造故障后系统的暂态能量函数V(x)

2. 计算临界能量Vcr

3. 计算系统在扰动最后时刻即故障切除瞬间的暂态能量Vcl；

4. 通过比较Vcl和Vcr直接判断系统的暂态稳定性，如果Vcl＞Vcr，则系统不稳定，否则系统稳定。两者之间的差Vcl-Vcr称为能量裕度或稳定裕度。

从稳定和稳定域理论的角度，上述步骤可以理解为计算故障后系统的稳定平衡点的稳定域（吸引域），并判断故障清除时刻的系统状态是否处于稳定域内。

应用暂态能量函数法最困难的一步是要计算临界能量Vcr，利用恒值能量曲面(x|V(x)=Vcr)来近似估计稳定边界s()Ax∂。主导UEP法基于扰动后的系统轨迹从某个UEP附近逸出稳定域这一规律，利用主导不平衡点(Controlling Unstable Equilibrium Point, CUEP)处的能量作为临界能量。计算过程分为两步:识别扰动模式和数值计算CUEP。

识别扰动模式或失稳模式，即识别失稳的临界机组，通常通过时域仿真来识别。CUEP是与扰动模式相关的UEP，和SEP一样都是潮流方程的解，可利用牛顿法来求解，区别主要是初值的选取不同。本文选用BCU法来数值求解CUEP。

3 主动解列的可行解列时刻

3.1可行解列时窗的特征

解列的过程非常复杂，涵盖了解列前的系统失稳阶段和解列后的孤岛过渡阶段，解列前的场景变化（拓扑结构、运行方式、扰动位置等）和解列过程中的参数变化（扰动持续时间、解列地点、解列时刻等）都会引起不同的解列动态过程和响应，但其中的暂态稳定问题都可以用稳定和稳定域的理论予以分析和解释。

从稳定和稳定域理论的角度，解列的过程包括每个孤岛子系统从一个稳定平衡点（扰动前稳定运行点）到另一个稳定平衡点（解列后孤岛的稳定运行点）之间的动态过程。也就是说，一旦解列断面确定，每个孤岛对应的解列后稳定运行点和稳定域就确定了；而判断某个孤岛在解列后是否稳定，就是判断在解列操作时，系统运行轨迹是否处于该孤岛的稳定域内。单个孤岛的可行解列时窗就是在故障清除后的动态过程中，系统轨迹处于该孤岛稳定域内的时段；整个系统的可行解列时窗则是各孤岛可行解列时窗的交集。

为了研究在解列动态过程中孤岛的暂态稳定性及其对解列时刻的要求，需要将暂态稳定分析的对象和视角转向每个孤岛，分析每个孤岛在解列过程中特别是解列前的运行轨迹，而不能再采用忽略孤岛内暂态稳定的单机等值模型。

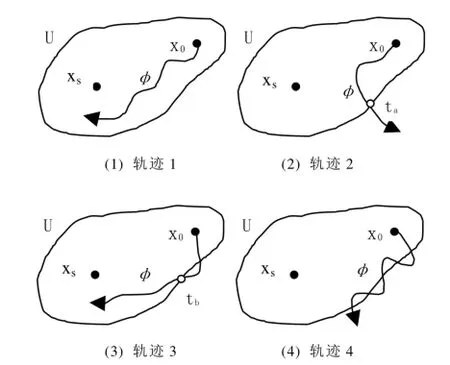
图1 解列前孤岛运行轨迹示意图Fig.1 An illustration of island stability

考虑扰动过程中孤岛运行轨迹和稳定域之间的关系，可行解列时窗的分布可能对应以下五种情况:

（1）扰动过程中解列前的孤岛运行轨迹如图1（1）所示，在故障发生、故障清除、系统失步/持续振荡的过程中，孤岛的运行轨迹始终在自己的稳定域内，此时无论何时解列，孤岛均能稳定运行，平稳过渡到稳定运行点xs。

（2）解列前的孤岛运行轨迹如图1（2）所示，在系统失步/持续振荡过程中，孤岛内的同步性发生了变化，孤岛运行轨迹在某个临界时刻ta逸出稳定域。这种情况下，如果在该临界时刻前解列，孤岛可以过渡到稳定运行点，如果在临界时刻后解列，孤岛将失去稳定性。该临界时刻ta由孤岛未解列前运行轨迹和孤岛稳定域的交点所确定。

（3）解列前的孤岛运行轨迹如图1（3）所示，在故障清除过程中，孤岛的运行轨迹短时逸出稳定域。由于此时并未解列，孤岛仍受系统其他部分的影响，持续一段时间后运行轨迹又进入到稳定域中，此时的可行解列时窗呈现出大于某个临界时刻的特点，该临界时刻tb由孤岛运行轨迹进入稳定域的交点所确定。

（4）解列前的孤岛运行轨迹如图1（4）所示，在故障清除后的系统失步/振荡阶段，孤岛内的发电机之间出现持续振荡，孤岛的运行轨迹在稳定域边界持续振荡，此时的可行解列时窗呈现出断续的多时窗分布特点，经过几个振荡周期后，孤岛可能失稳或趋于稳定。

（5）除了上述四种运行轨迹外，还有两种情况，一种是由于解列策略的不合理导致孤岛根本不存在稳定运行点xs，另一种是孤岛的初始运行点处于其稳定运行点xs的稳定域外。这两种情况下，孤岛的可行解列时窗均为空，无论何时解列，孤岛都不能稳定运行。

通过上述分析可以看到，类似于利用故障清除时刻的能量与临界能量相比来评估系统扰动后的稳定性，孤岛的稳定性可以用解列操作时刻的能量与孤岛失稳的临界能量相比较来进行评估。对孤岛而言，故障发生、故障清除、系统失稳/振荡都属于扰动过程，而扰动的结束时刻即解列操作的执行时刻。

与判断系统是否需要解列时将系统等值为双机系统或单机无穷大系统的方法不同，评估解列后孤岛是否稳定，应当将视角转向每个孤岛在解列过程中的暂态稳定性分析，即分析孤岛内发电机之间的同步关系。首先，解列后形成的每个孤岛必须有合理的稳定运行点，没有稳定运行点的孤岛除非进一步采取特殊的控制措施，否则不可能稳定运行；第二，在判断出系统振荡/失稳时，系统运行点必须位于孤岛的稳定域内，且距离稳定边界有一定的距离；第三，执行解列操作时，系统运行点必须位于孤岛稳定域的稳定边界内；第四，孤岛的可行解列时窗就是解列过程中系统轨迹处于孤岛稳定域的稳定边界之内的时段。

3.2基于能量函数法的可行解列时窗计算

为了验证以上分析，本文采用能量函数法[11]对解列的动态过程进行量化评估。为简化分析，采用不带控制的两阶发电机经典模型和恒阻抗负荷模型，并在计算过程中将系统收缩到发电机内节点进行时域仿真和能量函数的计算。

基于网络化简模型的能量函数法主要步骤包括:

（1）针对每一个解列策略，分别计算解列后每个孤岛的稳定平衡点，并根据式（1）构建该孤岛的能量函数(,)Vδω。

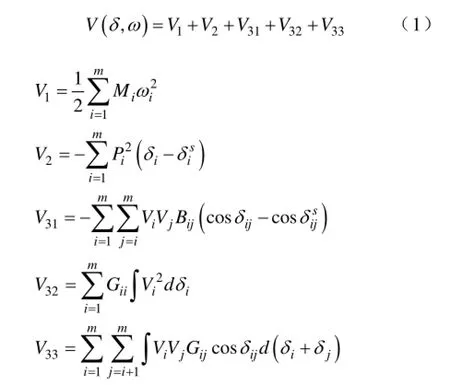
其中，iV和iδ为发电机i的内电势幅值和功角，Bij和Gij为节点i和j之间的等效电纳和电导，δij为点i和j之间的功角差。

（2）设定故障发生时刻、故障清除时刻，然后经过一定延时后对系统进行解列，并利用BCU法计算该孤岛的主导UEP（Controlling Unstable Equilibrium Point, CUEP）。

（3）针对每个孤岛，计算主导不稳定平衡点的能量作为该孤岛的临界能量。

（4）通过每个孤岛的临界能量和持续不解列场景下孤岛的积分轨迹，来确定该孤岛的可行解列时窗分布。

（5）取所有孤岛的可行解列时窗分布的交集，作为整个系统的可行解列时窗。

本文所定义的可行解列时窗(Feasible Splitting Time Interval, FSTI)，是暂态稳定意义下的可行解列时刻，即在该可行时窗内解列，形成的孤岛一定是暂态稳定的；在该可行时窗外解列，所形成孤岛的暂态稳定性不能保证。

3.3频率稳定性对可行解列时窗的修正

为使得孤岛实现稳定运行，除了孤岛内的暂态稳定需要满足以外，解列后孤岛的频率偏移也不能过大，否则将触发发电机的频率保护。在满足孤岛暂态稳定的可行解列时窗的基础上，可以利用发电机频率保护定值作为最大频率偏移对解列时窗进一步修正。修正后的可行解列时窗FSTI′将同时满足孤岛暂态稳定和频率偏移的要求。

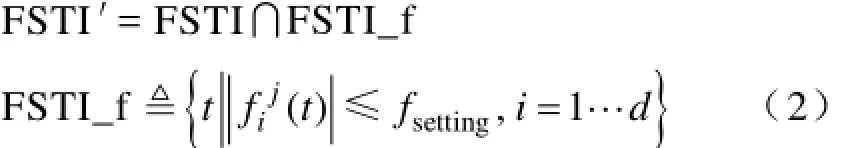
其中，d是解列形成孤岛的数目，t是某一时刻点，fj(t)是在t时刻孤岛i中发电j的频率偏移，

i fsetting为允许的最大频率偏移。

在修正后的可行解列时窗FSTI′内，每个孤岛内的发电机群均保持同调性并满足频率偏移要求，逐渐过渡到其各自的稳定运行点。

限于篇幅，本文主要研究暂态稳定意义下可行解列时窗的计算和分布特征，这是解列时刻选取的第一步，也是最难的一步。对考虑频率稳定性的时窗修正仅做概念上的简单介绍。

4 仿真分析

4.1可行解列时窗的计算

为了刻画出可行解列时窗的分布特点，本文利用能量函数对解列过程进行量化分析，得到解列过程中各孤岛能量变化的轨迹。

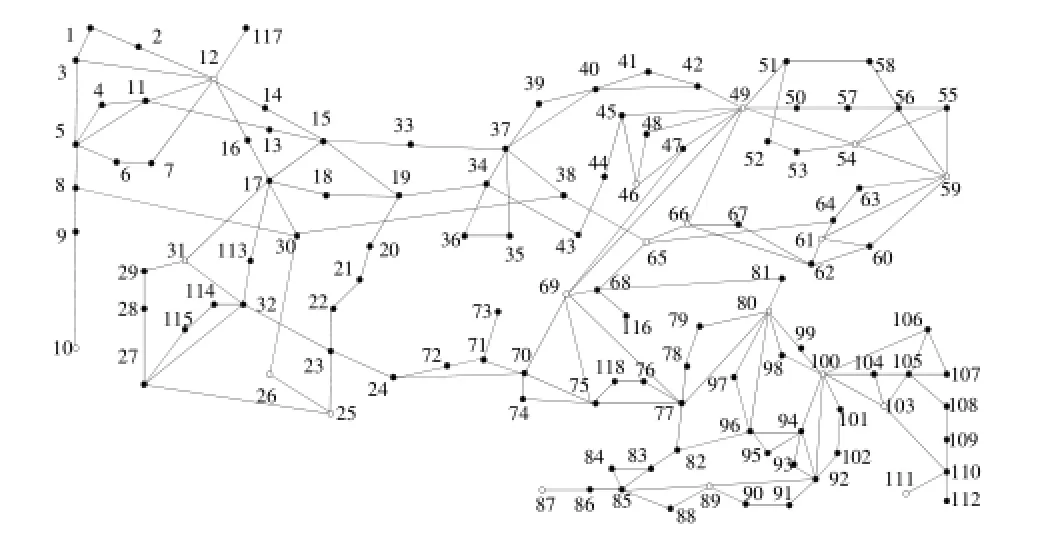
图2 IEEE118节点系统Fig.2 IEEE 118-bus test system diagram

以图2所示的IEEE118节点系统为例，选用了发生同一地点的同一故障（0.1s在线路23-25上靠近母线25处发生三相短路故障）作为扰动事件，通过设置故障清除时刻T1 (T1时刻跳开线路23-25清除故障)来形成扰动场景。为简化分析，发电机采用经典模型，AVR和调速器均禁用，发电机参数如附录I所示。

选取解列时刻T1=0.80s，发电机功角曲线如图3所示。可以看到，IEEE 118节点系统中出现了两机群:临界机群Group1{10,12,25,26,31}和剩余机群Group2:{46,49,54,59,61,65,66,69,80,87,89,100,103,111}失步，机群1内部随时间持续不能保持同步，发电机G31将失稳。

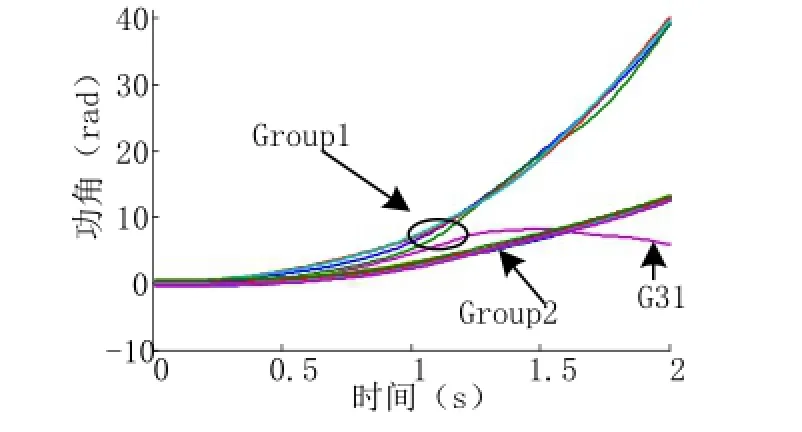
图3 故障清除时刻为0.8s的发电机功角曲线Fig.3 Rotor angles with the fault clearing time 0.8s

选取解列策略{15-33, 19-34, 30-38, 23-24}，可以将系统分割为两个部分:孤岛1和孤岛2，分别包含机群Group1和Group2。

选取图4(1)所示的孤岛1作为研究对象，利用BCU法可以得到故障后SEP为{0.1397,-0.3485, 0.1083,0.1478,-0.524}，主导UEP为{-0.2812, -0.7959,-0.3086,-0.2469,2.743}。故障发生、故障清除及系统振荡/失步过程中孤岛1的暂态能量变化如图4(2)所示，其中的蓝色实线为孤岛1在清除故障但未解列时的暂态能量，红色点划线对应着主导UEP的临界能量2.974 pu。根据主导UEP的临界能量可以计算出临界的解列时刻为0.94s，这种情况对应于图1（2）的运行轨迹。

应当特别指出的是，这里虽然选用解列策略{15-33, 19-34, 30-38, 23-24}作为孤岛1的边界，但并未执行解列策略，所以孤岛1内的能量并不守恒。

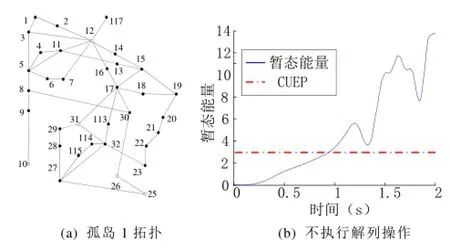
图4 0.80s清除故障时孤岛1的暂态能量变化Fig.4 Transient energy of island 1 with the fault clearing time 0.80s

在0.94s和0.97s分别进行解列时，孤岛的能量变化如图5(1)-(2)所示，其中，0.94s解列时孤岛1可以稳定，而0.97s解列时孤岛1失去稳定，解列后孤岛的能量均保持恒定。由于暂态能量函数法具有一定的保守性，通过能量函数求得的临界解列时刻0.94s略小于实际的临界解列时刻0.96s。

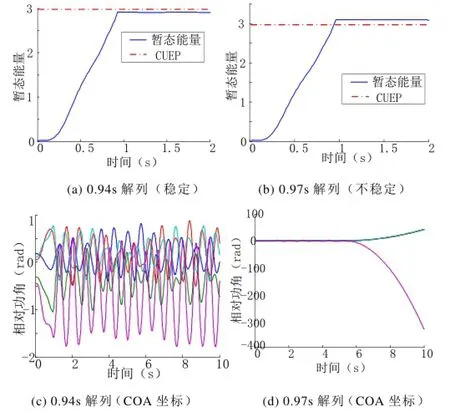
图5 0.94s和0.97s解列时孤岛1的暂态能量和功角Fig.5 Transient energy of island 1 with the fault clearing time 0.80s

通过大量时域仿真可以观察到，不管故障清除时间如何变化，解列后孤岛1的失步模式始终为发电机31失步这一种失步模式，即对应着同一个主导UEP。这一特点使得本例的分析简单很多，这也是图4中主导UEP的临界能量能够表示为一条直线的原因。

4.2可行解列时窗的分布特征

在本文中，由于固定了发生故障的位置和故障类型，故障持续时间成为影响可行解列时窗的一个非常重要的因素。除了4.1中故障清除时刻为0.8s的算例以外，为进一步研究可行解列时窗的分布特征，分别选取故障清除时刻T1=0.61s, 0.72s, 0.73s和0.94s的解列场景进行研究。

图6(1)为T1=0.61s时，孤岛1在扰动过程中的暂态能量变化。可以看到，此时在任何一个时刻执行解列操作，孤岛1的暂态能量均小于主导UEP所对应的临界能量，孤岛1始终会稳定，这种情况对应于图1（1）的运行轨迹。

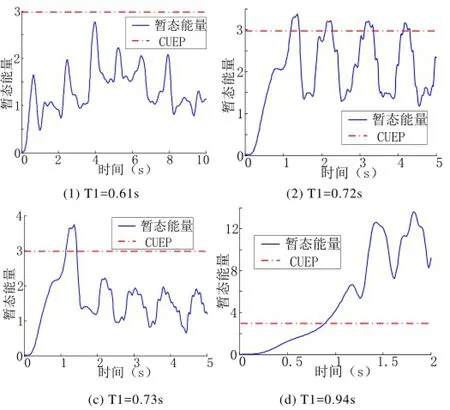
图6 不同故障清除时间时孤岛1的暂态能量变化Fig.6 Transient energy of island 1 with different fault clearing times

当T1=0.72s时，由于机群Group1在0.72s故障清除后始终未完全失去同步，处于振荡过程中，孤岛1的暂态能量出现了持续振荡，从而使得可行解列时窗呈现多时窗分布的特点（如图6（2）所示，对应图1（4）的运行轨迹）。

当T1=0.73s时，这种振荡是快速衰减的，孤岛1的暂态能量在短时超出临界能量后，快速回到稳定域内，此时的可行解列时窗将大于某个临界值（如图6（3）所示，对应图1（3）的运行轨迹）。

由于暂态能量上升沿与主导UEP能量的交点可以比较准确的表征孤岛从稳定变为不稳定的临界解列时刻，但下降沿的交点不能准确表示从不稳定变为稳定的临界时刻[11]，所以图6（2）仅能作为持续振荡过程中暂态能量变化的示意图，准确的可行解列时窗应通过时域仿真得到，如表I所示。

当故障清除时间达到0.94s时，无论何时解列，形成的孤岛均不能稳定运行，此时可行解列时窗为空。

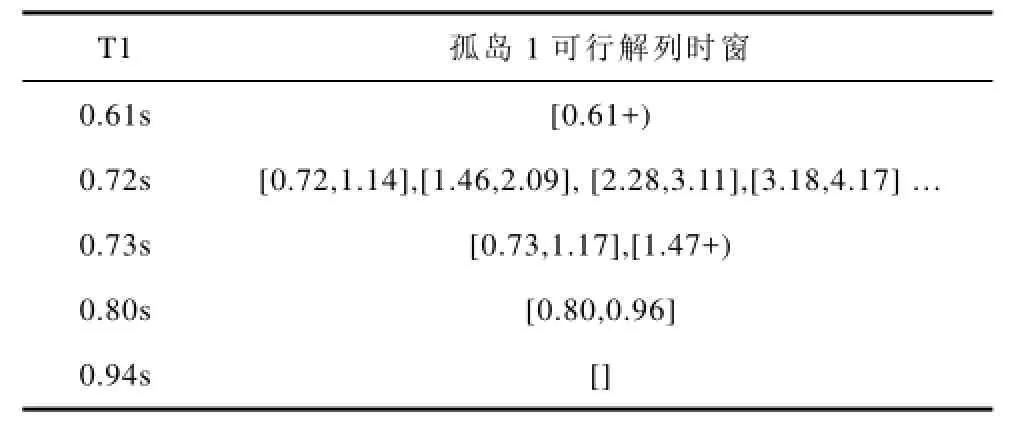
表 孤岛1的可行解列时窗（时域仿真）Tab. Feasible splitting time interval of island 1

另外，不同故障清除时刻所对应孤岛2的稳定性均较好，无论何时解列，解列后的孤岛2均可稳定（对应于图1（1）的运行轨迹），所以本文主要分析孤岛1的稳定性和可行解列时窗。从这里也可以看到，包含临界机群的孤岛往往较小，稳定性较差，对解列时刻和解列断面的要求较高；而包含剩余机群的孤岛相对比较稳定。但如果在包含剩余机群的孤岛内发生后继扰动，则很有可能破坏孤岛的稳定性，使得该孤岛失稳或进一步解列。

综合来看，由于故障清除时刻引起的扰动背景不同，孤岛的可行解列时窗呈现出了五种不同的情况:1）任何时刻均可以解列，这种情况对应于扰动较小或孤岛较强壮的情况，在解列动态过程中孤岛内部的发电机始终保持较好的同步关系；2）小于某个临界时刻，此扰动背景下出现失步或持续振荡，在临界时刻之前解列，孤岛内的同调机群仍能够保持同步，最终过渡到稳定的孤岛运行，但大于临界时刻后解列，孤岛内的同调机群将失稳。3）大于某个临界时刻，如图6（3）中0.73s清除故障的情况，此时解列并不是越早越好，而是在某个临界时刻后解列才可以保证孤岛内机群的同步性。4）断续的时窗特征:当某个机群内部出现持续振荡时，整个解列时刻可能呈现出断续的时窗特征，如图6（2）中0.72s清除故障的情况。若该振荡快速衰减，则可能成为上述第三种情况。5）可行解列时窗为空:对应于图6（4）所示的情况，由于故障清除过晚致使可行解列时窗为空。

5 结语

本文采用暂态能量函数法对解列动态过程进行了量化分析，刻画了不同扰动背景下系统可行解列时窗的分布特征，对主动解列的可行解列时窗进行了系统性分析。在研究方法上，首次将暂态稳定分析的对象和视角转向每个孤岛（解列后子系统），分析每个孤岛在解列过程中内部的暂态稳定和对解列时刻的要求，而不再仅采用忽略孤岛内暂态稳定的单机等效模型。

研究表明，解列时刻并不是越快越好。在本文中，由于故障清除时刻引起的扰动背景不同，孤岛的可行解列时窗呈现出了五种不同的情况:1）任何时刻均可解列；2）小于某个临界时刻；3）大于某个临界时刻；4）断续的时窗特征；5）可行解列时窗为空。在可行解列时窗范围内执行解列操作，形成的孤岛可以稳定运行；在可行解列时窗范围外执行解列操作，形成的孤岛无法稳定运行。

结合能量函数和时域仿真，本文首次尝试从机理上解释和刻画解列时刻的特征，为进一步研究主动解列问题提供了新的思路和支撑。当然，本文中也存在一些不足，例如仅考虑了发电机经典模型和恒阻抗模型，未考虑AVR和调速器的控制作用，得到的可行解列时窗非常保守，尺度很小。未来工作将考虑引入发电机高阶模型和控制措施，采用更符合实际的算例，并进一步研究解列时刻的在线决策方法。

附录1 118节点系统的发电机数据Generator data for the IEEE 118-bus test system on a base of 100 MVA

[1] Senroy, N., Heydt, G.T. Timing of a controlled islanding strategy[C]. Transmission and Distribution Conference and Exhibition, 2005/2006 IEEE PES, 21-24 May, 2006, Dallas, USA:1460-1466.

[2] K. Sun, K. Hur, P. Zhang, A new unified scheme for controlled power system separation using synchronized phasor measurements [J]. IEEE Trans. Power Systems, 2011, 26(3):1544-1554

[3] M. Jin, T. S. Sidhu, K. Sun, A new system splitting scheme based on the unified stability control framework[J]. IEEE Trans. Power Systems, 2007, 22: 433-441.

[4] Q. Zhao, K. Sun, D. Zheng, J. Ma, Q. Lu, A study of system splitting strategies for island operation of power system: a two-phase method based on OBDDs [J]. IEEE Trans. on Power Syst., 2003, 18(4): 1556-1565.

[5] Y. Qiao, Study on the active splitting control scheme of large-scale power systems, Ph.D Thesis, Tsinghua Univ., Beijing, 2007.

[6] L. Ding, F. Gonzalez-Longatt, P. Wall, V. Terzija, Two-step spectral clustering controlled islanding algorithm, IEEE Trans. on Power Syst., 2013, 28(1): 75-84.

[7] C. Wang, B. Zhang, Z. Hao, J. Shu, P. Li, Z. Bo. A novel real-time searching method for power system splitting boundary. IEEE Trans. on Power Syst., 2010, 25(4): 1902-1909.

[8] P.A. Trodden, W.A. Bukhsh, A. Grothey, K.I.M. McKinnon, MILP formulation for controlled islanding of power networks, International Journal of Electrical Power & Energy Systems, 2013, 45(1): 501-508.

[9] 宋洪磊, 吴俊勇, 吴林峰, 电力系统紧急情况下的动态分区和自主解列策略, 电工技术学报, 2012.

[10] 卢芳，于继来，基于网络能量的电力系统失步解列方案[J]. 哈尔滨工程大学学报, 2011,32(6):780-785.

LU Fang, Yu Jilai, A method of power system outof-step separation based on network energy[J]. Journal of Harbin Engineering University, 2011, 32(6): 780-785.

[11] H. Chiang, Directed methods for stability analysis of electrical power systems [M]. Wiley Press, 2011.

Research on feasible splitting time interval of controlled islanding

Ding Lei1 Guo Yichen1 Chen Qing1 Vladimir Terzija1,2
（1. Key Laboratory of Power System Intelligent Dispatch and Control of the Ministry of Education (Shandong University) Jinan 250061 China; 2. The University of Manchester Manchester, UK, M13 9PL）

Controlled islanding is an active and effective way of avoiding catastrophic wide area blackout. The splitting time is the determining factor of successful islanding. However, it has not been well studied before since existing islanding methods are based on the system snapshots before disturbance occurrence and do not consider dynamic islanding process. This paper investigates the splitting time of controlled islanding systematically for the first time. Transient energy function is used to evaluate the stability of islands formed during the islanding process quantitatively. And the feasible splitting time interval is determined by the critical energy of islands to ensure the coherency and transient stability within created islands. Only when the splitting is undertaken within the feasible splitting time interval, the coherency within each island can be maintained and a successful islanding is possible.

Controlled islanding, Feasible splitting time interval, Stability region, Transient energy function

TM712

丁 磊 男，1980年生，博士，副教授，主要研究方向:电力系统广域保护控制和微电网保护控制。

国家自然科学基金资助项目（51477093，51107071）。

2014-07-10

郭一忱 男，1990年生，硕士研究生，主要研究方向：电力系统主动解列。