物元理论和证据理论相结合的电能质量综合评估

李玲玲 刘敬杰 凌跃胜 周 贤 张云龙

物元理论和证据理论相结合的电能质量综合评估

李玲玲1,2刘敬杰2凌跃胜1,2周 贤2张云龙2

（1. 河北工业大学河北省电磁场与电器可靠性省部共建重点实验室 天津 300130 2. 天津大学电气与自动化工程学院 天津 300072）

针对电能质量综合评估中存在的不确定性及主观性，提出了一种基于物元理论和证据理论相结合的电能质量综合评估方法。该方法运用可拓学中的物元理论建立电能质量的物元模型，利用关联函数将电能质量各项评估指标与各个质量等级的评价区间之间的隶属关系定量化，并将其进行归一化处理，进而获得各指标的基本信度函数；然后利用熵权法与G1法相结合的复合赋权法确定电能质量各评估指标的权重，用来修正原始证据的基本信度函数，在此基础上，利用证据组合规则对其进行融合，从而得到电能质量的综合评估结果。实例计算表明，该方法最大限度地减少了评估过程中的不确定性，能够得到更精确、客观的综合评估结果。

电能质量 物元理论 证据理论 综合评估

1 引言

电能质量是电网运行的三大目标之一[1]，科学合理地综合评估电网的电能质量是约束、督促电力公司与电力用户共同维护公共电网电能质量环境[2]的基础，同时也是衡量电能质量优劣和制定电价的主要依据，具有深刻的理论和现实意义。

目前，电能质量的综合评估方法主要有基于模糊数学[3]的评估方法、概率统计与矢量代数法[4-5]、基于灰色理论的评估法[6-7]、基于主客观权重的评估法[8-10]、雷达图法[11-12]和投影寻踪法[13]等。上述方法在评估过程中都存在一定程度的不确定性或主观性太强的问题，如文献[3]采用区间平均分布密度的概念建立了电能质量评价的模糊模型，但在确定权重值时采用了单一的主观赋权法，这对电能质量评估结果的准确性有很大影响；文献[5]依据电能质量各单项指标的主要特征，采用矢量代数方法有效地将其归一量化，然而选取不同的基准值会产生不同的评估结果，不利于电能质量的客观评价。基于遗传投影寻踪的电能质量评估法可以利用自动搜索提取高维非线性评估指标的特征，克服了传统评估方法中人为主观因素的缺陷，但是由于其自身评估过程中存在的隐蔽性，从而增加了评估结果的不确定性。

鉴于上述方法所存在的不足，本文引入了能有效处理不确定信息的证据理论和能解决事物各个特征不相容问题的物元理论。首先利用物元理论对电能质量的各个指标进行定量分析，并构造一种简单而有效的函数对定量的指标进行归一化，以得到各指标的基本信度分配函数；然后利用组合赋权法得到各指标的权重；最后，在此基础上再利用证据理论组合规则对电能质量的各个指标进行融合，从而得到更为客观、合理、精确的综合评估结果。

2 物元理论与证据理论基础

2.1物元理论

物元理论由我国学者蔡文在1983年提出，研究的是事物的质与量的内在联系及变化规律，利用关联函数的概念来表示事物具有某种性质的程度，能够从定性和定量两个角度客观地描述事物所处的状态。

（1）物元的概念。

定义1给定事物的名称N，它关于特征c的量值为v，以有序三元R=(N,c,v)作为描述事物的基本元，简称物元。如果一个事物的特征表现在多个方面，即以n个特征c1,c2,…,cn和相应的量值v1,v2,…,vn描述，则称R为n维物元，简记R=(N, c, v)，可用矩阵表示为

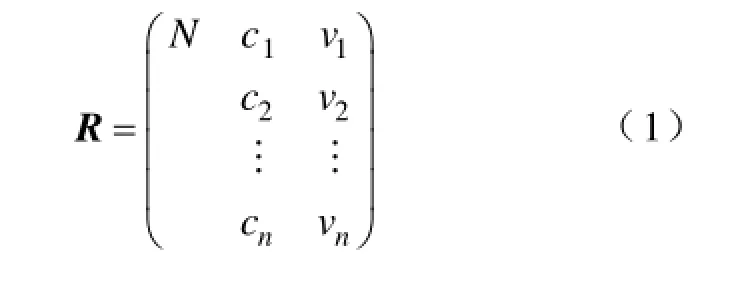
（2）经典域与节域。经典域是指待评估对象各个评价等级关于对应特征所规定的量值范围，经典域矩阵可表示为

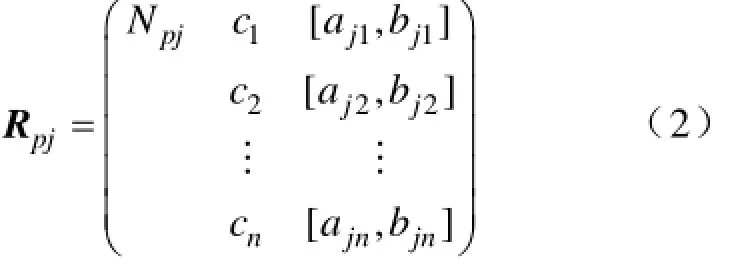
式中，Npj为事物N的第j个评价等级；[apj, bpj]为特征量cn隶属于第j个评价等级时所规定的量值范围。

节域是指待评估对象评价等级的全体关于某些特征所规定的量值范围，节域矩阵可表示为

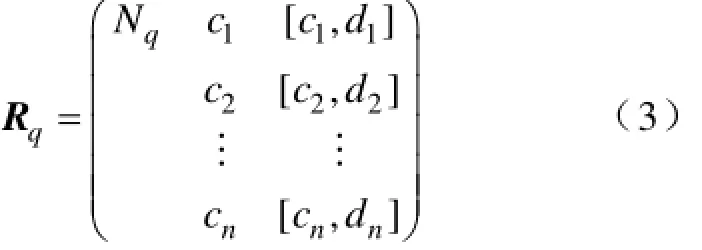
式中，Nq为事物N的评价等级的全体；[cn, dn]为特征量cn所有评价等级所规定的量值范围。

（3）关联函数。关联函数描述的是物元中的元素到实轴上的映射，具体表述为论域中的任意一点x与两个区间经典域Xpji=[aji, bji]和节域Xqi=[ci, di]的量化关系。通过关联函数，可以定量客观地描述元素隶属于某一性质的程度及其变化，而且对同一域内的元素，也可以根据关联函数值（即关联度）的大小区分出不同的层次。为定量描述物元特征，将实变函数中距离的概念拓展为距，则实域轴上的任意一点x与有限区间X=[a, b]的距的计算公式为

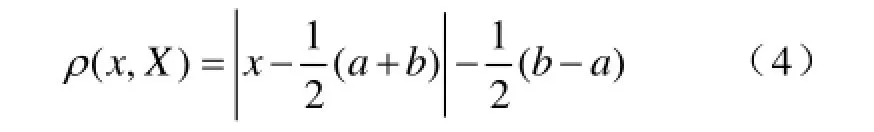
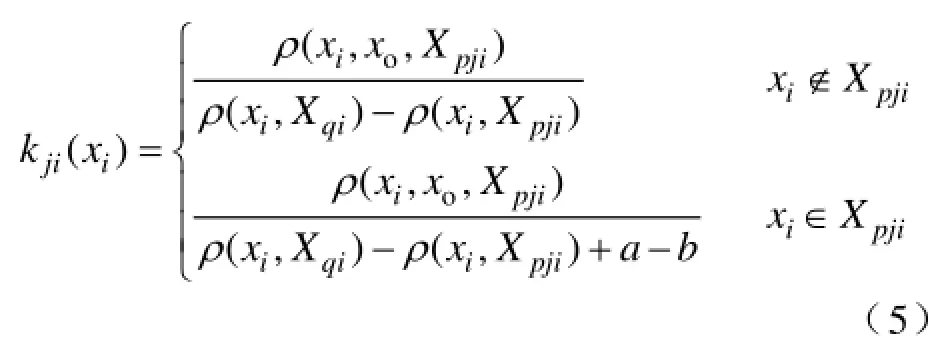
假设xo表示关联函数取最大值时的点，即最优值点，最优值点的位置不同，则所用的关联函数也不同。当最优值点不是经典域的中点时，其关联函数的公式为式中，kij为评价体系中第i个评估指标隶属于第j评价等级的程度。其中ρ(xi,xo,Xpji)表示侧距，若最优值点，则称其为左侧距，其计算公式为

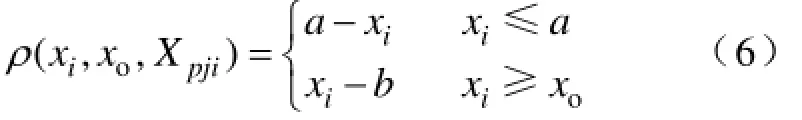
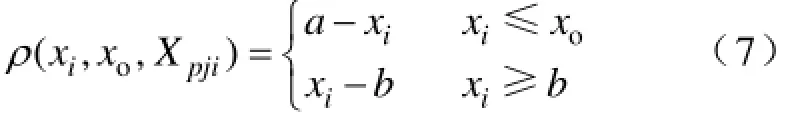
2.2证据理论

证据理论起源于1967年Dempster提出的由多值映射导出的上概率和下概率，后来由Shafer对其进行推广和完善，并使之形成一种系统化、理论化的不确定性推理的理论。它最显著的特点是能够处理由不确知引起的不确定性，为不确定信息的表达与合成提供了有效的方法。

定义2证据理论用辨别框架Θ=｛θ1,θ2,…,θm｝表示由互斥且穷举的命题所构成的集合，按传统方法把Θ的冥集表示为2θ，即Θ的所有子集的集合。对应于识别框架Θ上的一个集函数m: 2θ→ [0,1]，若满足，则称m为辨别框架Θ上的基本信度分配函数。

m(A)的含义如下[14]:①若AΘ⊂且AΦ≠，则m(A)表示对命题A的精确信任度；②若AΘ=，则m(A)表示对命题A中所含不确定性的量度。

定义3AΘ∀⊆，若m(A)＞0，则称A为m的一个焦元。设m1、m2是同一辨别框架Θ上的基本信度分配函数，焦元分别为A1, A2,…, At和B1, B2,…, Bl，记m1和m2的合成结果为m1⊕m2，则D-S合成法则表示为

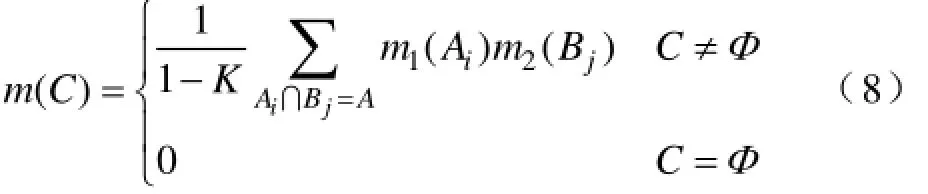
其中

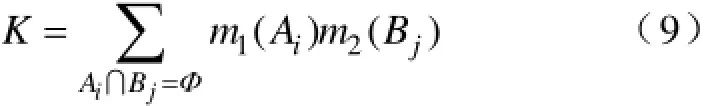
式中，i=1,2,…, l; j=1,2,…, t。

3 基于物元理论的证据的获取与权重证据合成

3.1基于物元理论的证据基本信度函数的获取

证据理论能够直接表达不确定性，为不确定信息的表达与合成提供了有效的方法。但是其证据主要是通过专家的知识和经验得到，具有很强的主观性。物元理论中所提出的物元的概念为事物的分类和模式识别提供了新的途径，物元理论通过关联函数可以定量客观地描述元素隶属于某一性质的程度及其变化，而且对同一域内的元素，也可以根据关联函数值（即关联度）的大小区分出不同的层次。利用物元理论的分类思想和隶属度概念，并经过归一化的处理，能够建立证据理论的辨别框架，进而获得证据理论辨别框架上的基本信度函数。同时，物元理论能够有效地把事物中存在的矛盾问题转换为相容的，因而能够减少证据理论中各个证据之间的冲突，从而能最大限度地优化证据融合的结果。

在物元理论中，与可拓集合相应的关联函数的概念把逻辑值从{0,1}扩展到(,)-∞+∞，利用关联函数值（即关联度）的大小来判断元素与集合的从属关系，使经典域中元素与集合非此即彼的定性描述扩展为定量的描述，从而能够更全面、精确地表征集合中元素间的层次关系。

当关联函数k(x)＞0时，表示元素具有某一性质，且值越大越接近该性质；当关联函数k(x)=0时，元素为临界元素，表示有可能具有某一性质，也可能不具有该性质；当关联函数k(x)＜0时，表示元素不具有某一性质，且值越小越远离该性质。用证据理论的语言表述为:关联函数的值越大，转换成证据的基本信度函数值也越大；反之，则转换成证据的基本信度函数值也越小。又证据理论的基本信度函数的值域是[0,1]，因此需要对物元进行归一化处理，才能建立符合证据理论要求的辨别框架。

记某一事物的物元为Kj=(kj1,kj2,…,kjm)，则转换成证据理论的辨别框架上的信度函数为mj:(mj(θ1),mj(θ2),…,mj(θm))。则归一化的计算公式为

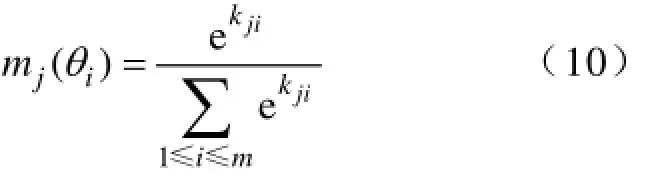
式中，因为指数函数ex是递增函数，所以该公式满足:kji的值越大，m(θi)越大；kji的值越小，mj(θi)越小；且0≤mj(θi)≤1（当kji→+∞时，mj(θi)=1；当jik→-∞时，可见该归一化函数符合常规思维逻辑推理，能够合理地过渡物元理论与证据理论之间的转换。

3.2基于权重的证据合成

3.2.1 熵权法

熵原本是热力学中的一个物理概念，是体系混乱度（或无序度）的量度，最先由申农（C. E. Shannon）将其引入信息论中，称之为信息熵。熵可以用来表征事物出现的不确定性的概念，即可以度量数据所提供的有效信息量。如果评价对象某一指标的熵值越小，则表征该指标所携带的信息量越大，其在综合评价就中所起的作用也越大，则指标的权重也越大；反之，则指标的权重就越小。

假设评价对象有n个待评指标，每个指标都有m种不同的状态（即评价等级），则第i个指标的信息熵的计算公式为

㉚对于现象学诸观念理解，受张祥龙研究启发甚多，可参看张祥龙《朝向事情本身——现象学导论七讲》，团结出版社2003年版;张祥龙《海德格尔思想与中国天道》，北京三联书店1996年版;张祥龙《什么是现象学》，《社会科学战线》2016年第5期。

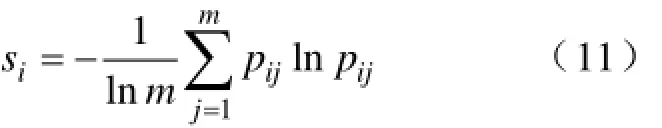
式中，pij为各个指标处于不同的状态的概率，若

第i指标的熵权wsi的计算公式为

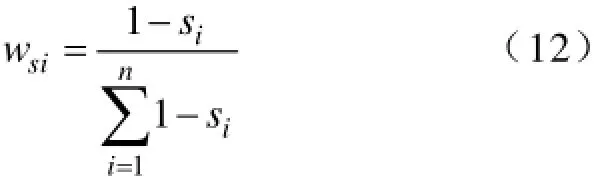
3.2.2 G1法

G1赋权法是我国学者郭亚军教授提出的一种新的主观赋权法，它是在层次分析法的基础上进行改进而来。该方法克服了层次分析法的缺点，在确定各指标权重过程中不需要构造判断矩阵，且无需一致性检验，从而减少了计算量，可操作性强，便于推广使用。下面简要介绍该方法确定权重的步骤。

（1）确定序关系。

定义4若评价指标Xi相对某评价准则（或目标）的重要程度大于（或不小于）Xj，记为Xi＞Xj。

定义5若评价指标X1,X2,…,Xm相对于某评价准则（或目标）具有关系式表示｛Xi｝按序关系“＞”排序后的第i（i=1,2,…,m）个评价指标。为了书写方便且不失一般性，式（13）中的仍记为Xi（i=1,2,…,m）。式（13）中的序关系是由专家根据相关经验并结合专业知识评定给出的。

（2）给出相邻指标之间相对重要程度的理性判断。设专家对评价指标1kX-和Xk的相对重要程度之比的理性赋值分别为

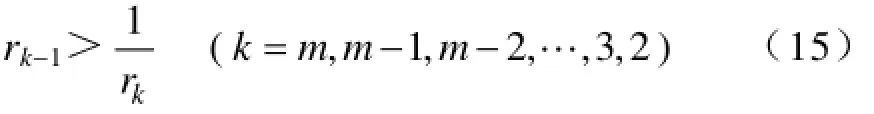
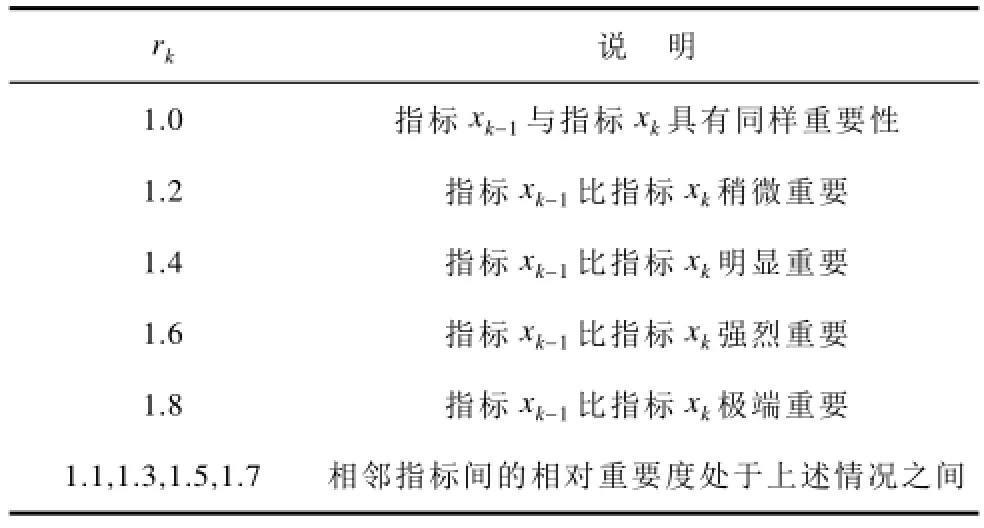
表1 rk赋值表Tab.1 The assignment table of rk

（3）用G1法所得的指标权重wk的计算。若专家给出的理性赋值满足关系式（15），则

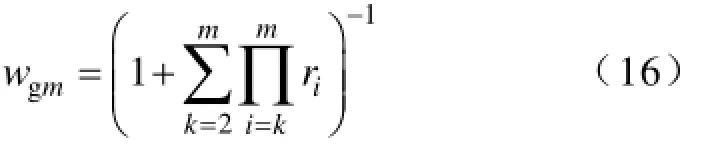
则可得指标权重

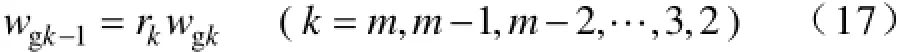
3.2.3 复合权重的计算

设已得出指标的熵权为wsi、用G1法求得的权重为wgi，依据最小鉴别信息原理，为了使复合权重和wsi、wgi尽可能地接近[15]，建立如下的复合权重函数

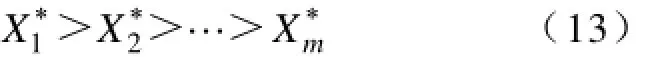
3.2.4 基于权重的证据合成

在经典的证据组合规则中，是同等看待各个证据，但在实际应用中，各个证据在融合时具有不同的重要性，即参与合成的各个评价指标在综合评估过程所起的作用是不同的，鉴于此，本文引入了权重因子以使证据的融合结果更加客观且符合常理。

假设某一评价系统具有n个不同的单项指标，且对每个指标有m个不同评价状态。通过物元变换建立证据的辨别框架Θ=｛θ1,θ2,…,θm｝，辨别框架中的各命题元素代表指标的的不同评价状态；则所得辨别框架上的基本信度函数为m:m1,m2,…,mn，且通过熵权法与G1法的科学组合的所得与其信度函数相对应的复合权重为

设wg=max(w1,w2,…,wn)，可得相对权重向量W*=(w,w,…,w)w，则

12ng

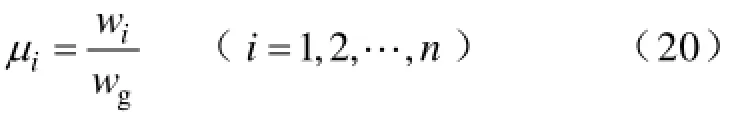
式中，μi称为量权，用来表征某一证据在所有证据中的重要性的量度。

用量权iμ处理后的证据源模型如下

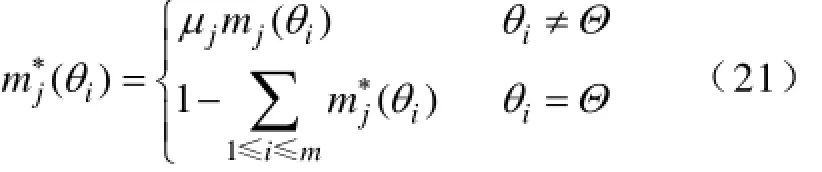
式中，i=1,2,…,m ；j=1,2,…,n。

4 电能质量的综合评估模型

电能质量的综合评估是在各单项指标评估的基础上建立起来的，如何用科学、合理的方法将多个单项指标综合为单一量化的指标是电能质量综合评估的关键。本文通过建立电能质量各指标的物元模型将其定量化，在此基础上，利用基于权重的证据理论将电能质量的各个指标进行科学的融合，从而得出客观、合理的综合评估结果。

4.1基于物元理论的电能质量单项指标的量化

本文以国家电网规范的六项电能质量标准作为评定电能质量综合评估的依据，将各项电能质量指标作为评估指标，电能质量的六项评估指标分别为频率偏差、电压总谐波畸变率、电压波动、电压闪变、电压偏差和电压三相不平衡度，并分别用16～ff表示。本文以国内某个风电场中外埔变电站110kV母线作为研究对象并对其电能质量进行综合评估，将电能质量的指标在国家标准规定的合格范围内分为四个质量等级:优质、良好、中等、合格，并分别用14～dd表示。电能质量各项指标的分级界限及其实测数据如表2所示。

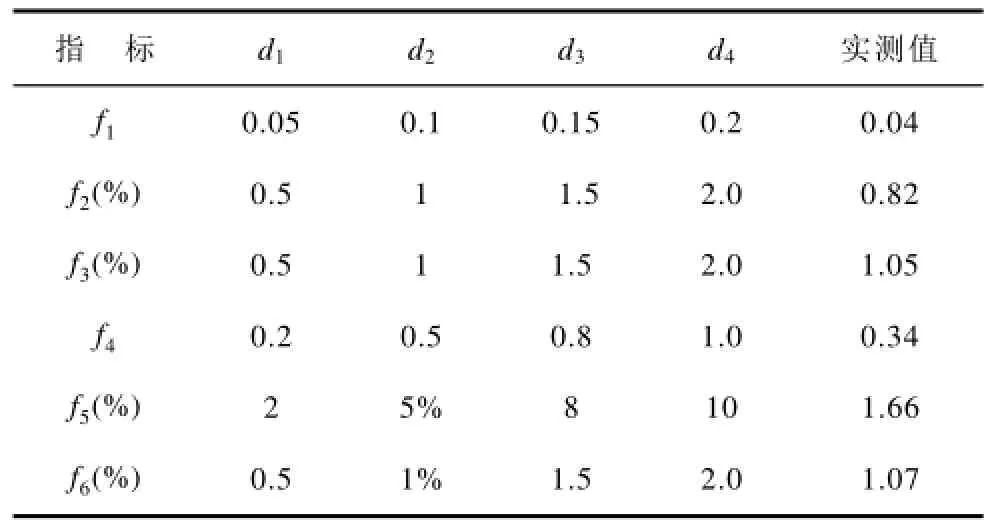
表2 电能质量各指标的分级标准及其实测数据Tab.2 Classification standard on index of power quality and its measured data

物元理论能从动态的、转化的角度对电能质量的评估指标进行分类，并以关联函数值定量地表示指标所属的质量等级，且关联函数的计算是以实际所测的客观数据为基础。

用Rp1表示电能质量等级为优质时的经典域物元矩阵，Np1表示电能的质量等级:优质，[0,0.05]表示在电能质量等级为优质时f1（频率偏差）的量值范围，根据实测数据可得

用Rq表示电能质量的节域物元矩阵，Nq表示电能质量的质量等级的全体，[0,0.2]表示电能质量在国家标准规定的合格范围内时f1（频率偏差）的量值范围，根据实测数据可得

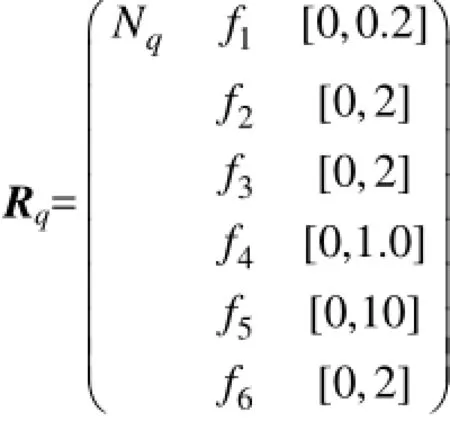
根据电能质量的特点可知，各指标的最优值在其经典域的左端点处取得，因此在计算关联函数时选用左侧距。以f1（频率偏差）为例计算，其实测值为0.04，又知Xp11=[0,0.05]，xi=0.04≥xo，xo=0∈[0,0.025]，则由式（4）和式（5）可得同理可得

用同样的分析计算步骤可得其他各个指标的关于所属评级等级的关联度，经计算后得到如下关联度矩阵

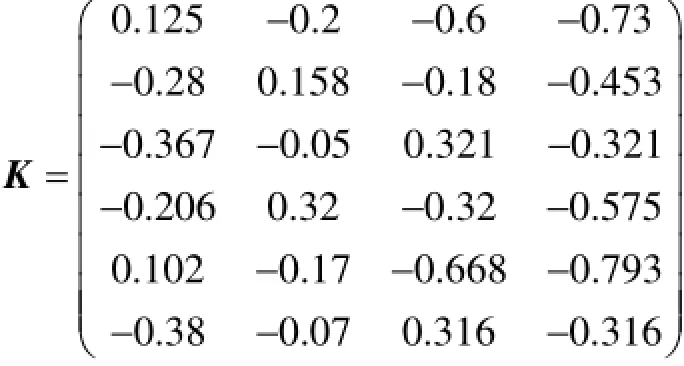
4.2电能质量评估模型中证据信度函数的获取

本文选取频率偏差、电压总谐波畸变率、电压波动、电压闪变、电压偏差和电压三相不平衡度六个指标作为评估电能质量的证据。根据电能质量的特点，建立基于证据理论的电能质量的质量等级的辨别框架Θ=｛θ1,θ2,θ3,θ4｝，框架中各命题元素表示电能质量的评价等级，且依次代表为优质、良好、中等、合格，建立在证据辨别框架Θ上的信度函数分别用m1～m6表示。则根据4.1节得出的电能质量的关联度矩阵，并将其数据代入式（10），即可得电能质量证据的信度函数为

4.3基于权重证据理论的电能质量综合评估

4.3.1 电能质量评估指标的权重获取

电能质量综合评估中，不同的电力用户及专家对电能质量的各个指标的重视程度不同，此外，电能质量的各个指标对电能质量的影响也不同，因此，在证据合成的过程中，需要综合考虑各个评估指标的主观权重和客观权重，才能得到更为客观、合理的评估结果。本文利用G1法和熵权法相结合的复合权重法确定电能质量的各个指标在评估过程中的权重。下面是求电能质量复合权重的步骤。

（1）电能质量各个指标的熵权的获取。本文中电能质量综合评估体系有六个评估指标，且每个指标有四种不同的质量等级状态，mi(θj)代表各个指标处于不同的质量等级状态的概率，则由式（11）可得:s1=0.9581，s2=0.9811，s3=0.970 4，s4=0.9582，s5=0.9530，s6=0.9703。

根据式（12）可得与f1～f6各项指标相对应的权重:ws1=0.2，ws2=0.1，ws3=0.142，ws4=0.2，ws5=0.225，ws6=0.142。

（2）基于G1法的电能质量各个指标的权重的获取。根据专家的意见和不同电力用户的要求，对电能质量的各个评估指标建立如下序关系:频率偏差＞谐波畸变＞电压波动＞电压闪变＞电压偏差＞电压三相不平衡度。

由表1可得理性赋值:21.8r=，31.7r=，r4=1.0，51.2r=，61.2r=。由式（15）可得与f1～ f6各项指标相对应的权重:wg1=0.37，wg2=0.205，wg3=0.121，wg4=0.121，wg5=0.1，wg6=0.083。

（3）电能质量各个指标的复合权重的获取。根据已求得的熵权和基于G1法所得的权重，并由式（16）可得与16～ff各项指标相对应的复合权重和权重向量:w1=0.283，w2=0.15，w3=0.136，w4=0.162，w5=0.156，w6=0.113，w=(0.283,0.15, 0.136, 0.162, 0.156, 0.113)。 4.3.2 基于证据理论的电能质量的综合结果

由上节所得的复合权重向量，可得wmax=0.283。则由式（20）可得量权:μ1=1，μ2=0.53，μ3=0.48，μ4=0.572，μ5=0.551。

用求得的量权按照式（20）修正证据的基本信度函数，在此基础上，再利用式（8）和式（9）得到证据的融合结果，用M1代表m1⊕m2⊕m3，M2代表m1⊕m2⊕m3⊕m4，M3代表m1⊕m2⊕m3⊕m4⊕m5，M4代表m1⊕m2⊕m3⊕m4⊕m5⊕m6，则电能质量各指标的融合结果如表3所示。

表3 电能质量各个评估指标的融合结果Tab.3 The fusion results on various evaluation indexes of power quality

从表3可得出证据理论融合的最终评估结果，以信度的函数形式表示为:M4: (0.354,0.338,0.183, 0.113,0.012)。根据最大信度函数原则，得出电能质量的综合评估结果是优质。通过表3也可看出在指标融合的过程中，随着证据的不断加入，评估结果的不确定度也在不断地减少，可见，采用证据理论融合的方法能减少评估过程中的不确定，同时也能给出评估结果的不确定性度量；同时，这也得益于物元理论与复合权重弥补了证据理论的缺陷，物元理论能够通过指标的实测数据得到客观、可靠的证据信度函数，提高了评估过程的严谨性；通过指标所蕴含的信息并结合专家和用户的意见确定指标权重，避免了评估过程中存在的主观性，减少了证据合成时的冲突，进而能够得到更为符合逻辑的综合评估结果。

采用与本文方法同样的分级标准，分别利用文献[3]中的模糊数学方法，文献[10]中的组合赋权法，文献[12]中的雷达图法对该变电站进行电能质量综合评估。由文献[3]中的方法得到的模糊评价决策为:B=(0.108,0.806,0.08,0.06)，根据隶属度最大原则可知，电能质量的综合评估结果为良好。组合赋权法得到的综合评估值为2.880，即电能质量等级为良好，在雷达图法中采用多层次交互式算法计算得到电能质量指标权重向量为:w=(0.190,0.155,0.166, 0.177,0.155,0.112)，结合权重值并经过计算得出雷达图中各指标所在扇形区域的角度向量，在此基础上得到雷达图的面积和边长，并将其带入雷达评价函数，从而得出电能质量综合评估值为3.160，即电能质量等级为优质。对电能质量等级进行量化，并分别用区间[0,1]、[1,2]、[2,3]和[3,4]表示电能质量等级的合格、中等、良好和优质，则可知电能质量隶属于所属等级的程度是不同的。将上述各种方法的评估结果值归一到同一单位量级，其归一后的电能质量评估值为h=电能质量所属等级区间的右端点值+质量等级所属该区间的程度（h*）。其中，根据模糊数学方法和本文方法所得到的综合评估值经量化到区间[0,1]后所得的值，则可直接得出:=0.806，=0.333。组合赋权法和雷达法的电能质量综合评估值不是建立在[0,1]，因此需要换算，换算后的h*为:h*=（所属质量等级区间的右端点值-实际评估值）/所属质量等级的区间长度。综上，由模糊数学法、组合赋权法、雷达图法和本文的方法所得到的归一后的电能质量评估值分别为:h1=2.806, h2=2.880, h3=3.160, h4=3.333。下图为采用四种方法的电能质量综合评估结果的比较。

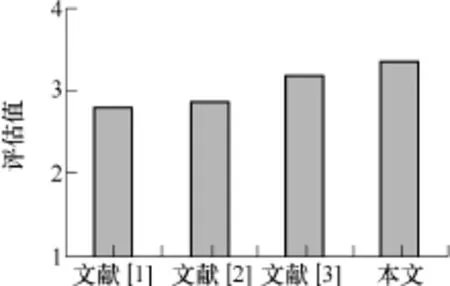
图 四种方法的综合评估结果对比Fig. Comprehensive evaluation results comparison among four methods

从上图可以看出，各种方法的综合评估结果有细微的区别，但基本近似。其中，文献[3]中的评估方法在确定权重时用的层次分析法主观性强，文献[10]中的方法避免了文献[3]方法的主观性，但是不能有效地处理评估过程的不确定性，因此，两种方法受单个指标等级偏低的三相不平衡度的影响较大，评估等级也较低。雷达图法和本文方法的评估结果基本一致，文献[12]中的方法无需数据的归一化处理过程，避免了归一化过程中可能出现的信息丢失现象，但该方法没有涉及处理评估过程中的不确定性的问题，因此仍待改进。本文的方法很好地弥补了上述方法的不足，可以更全面、客观地对评估对象的电能质量进行综合评估。

5 结论

本文利用物元理论与证据理论相结合的方法对电能质量进行综合评估，通过物元和关联函数的概念，将电能质量各项评估指标与各个质量等级的评价区间的关系定量化，并用关联值矩阵表示，然后对各指标的关联值进行归一化处理，从而获取各指标的基本信度函数，克服了证据理论产生基本信度函数时的主观随意性。在利用证据组合规则融合各评估指标的过程中，综合考虑了电能质量指标的主观权重和客观权重，既满足了专家和用户的要求，又实时、动态地体现了现场电能质量各指标数据的变化特点，同时，最大程度地提高了证据合成结果的客观、合理性。实例表明，该方法能科学地将电能质量多个单项指标综合为单一量化的指标，减少综合评估过程中的不确定性，得到更为精确、客观、合理的综合评估结果。但是该方法中的归一化过程可能造成部分有用的信息丢失，同时也增加了评估方法的复杂性；此外，在用证据理论对数据进行融合的过程中计算量大。因此，该方法仍需不断的改进，在实际的推广应用中还需实践的检验。

[1] 黄南天, 徐殿国, 刘晓胜, 等. 基于模式相似性测度的电能质量数据压缩方法[J]. 电工技术学报, 2011, 26(10): 39-46.

Huang Nantian, Xu Dianguo, Liu Xiaosheng, et al. Power quality data compression based on pattern similarity measurement[J]. Transactions of China Electrotechnical Society, 2011, 26(10): 39-46.

[2] 陶顺, 肖湘宁. 电力系统电能质量评估体系架构[J].电工技术学报, 2010, 25(4): 171-175.

Tao Shun, Xiao Xiangning. Infrastructure of the power quality assessment system of power systems[J]. Transactions of China Electrotechnical Society, 2010, 25(4): 171-175.

[3] 谭家茂, 黄少先. 基于模糊理论的电能质量综合评价方法研究[J]. 继电器, 2006, 34(3): 55-59.

Tan Jiamao, Huang Shaoxiang. Research on synthetic evaluation method of power quality based on fuzzy theory[J]. Relay, 2006, 34(3): 55-59.

[4] 熊以旺, 程浩忠, 王海群, 等. 基于改进AHP和概率统计的电能质量综合评估[J]. 电力系统保护与控制, 2009, 37(13): 48-52.

Xiong Yiwang, Cheng Haozhong, Wang Haiqun, et al. Synthetic evaluation of power quality based onimproved AHP and probability statistics[J]. Power System Protection and Control, 2009, 37(13): 48-52.

[5] 高雯, 王慧霞, 姚翠兰. 基于概率和矢量代数的电能质量综合评估[J]. 山西电力, 2009, 30(6): 65-67.

Gao wen, Wang Huixia, Yao Cuilan. Comprehensive evaluation of power quality based on probability and vector algebra[J]. Shanxi Electric Power, 2009, 30(6): 65-67.

[6] 雷刚, 顾伟, 袁晓冬. 灰色理论在电能质量综合评估中的应用[J]. 电力自动化设备, 2009, 37(11): 62-65.

Lei Gang, Gu Wei, Yuan Xiaodong. Application of gray theory in power quality comprehensive evaluation [J]. Electric Power Automation Equipment, 2009, 37(11): 62-65.

[7] 周辉, 杨洪耕, 吴传来. 基于灰色聚类的电能质量综合评估方法[J]. 电力系统保护与控制, 2012, 40(15): 70-75.

Zhou Hui, Yang Honggeng, Wu Chuanlai. A power quality comprehensive evaluation method based on grey clustering[J]. Power System Protection and Control, 2012, 40(15): 70-75.

[8] 李娜娜, 何正友. 主客观权重相结合的电能质量综合评估[J]. 电网技术, 2009, 33(6): 55-61.

Li Nana, He Zhengyou. Power quality comprehensive evaluation combining subjective weight with objective weight[J]. Power System Technology, 2009, 33(6): 55-61.

[9] 刘兵, 李群湛, 董祥. 基于时变权重的电能质量综合评估研究[J]. 电力系统保护与控制, 2009, 37(14): 6-9.

Liu Bing, Li Qunzhan, Dong Xiang. Comprehensive assessment study of the power quality based on the time-varying weight[J]. Power System Protection and Control, 2009, 37(14): 6-9.

[10] 李娜娜, 何正友. 组合赋权法在电能质量综合评估中的应用[J]. 电力系统保护与控制, 2009, 37(16): 128-134.

Li Nana, He Zhengyou. Combinatorial weighting method for comprehensive evaluation of power quality [J]. Power System Protection and Control, 2009, 37(16): 128-134.

[11] 乔鹏程, 吴正国, 李辉. 基于改进雷达图法的电能质量综合评估方法[J]. 电力自动化设备, 2011, 31(6): 88-92.

Qiao Pengcheng, Wu Zhengguo, Li Hui. Powerquality synthetic evaluation based on improved radarchart[J]. Electric Power Automation Equipment, 2011, 31(6): 88-92.

[12] 李国栋, 李庚银, 杨晓东, 等. 基于雷达图法的电能质量综合评估模型[J]. 电力系统自动化, 2010, 34(14): 70-74.

Li Guodong, Li Gengyin, Yang Xiaodong, et al. Acomprehensive power quality evaluation model basedon radar chart method[J]. Automation of Electric Power Systems, 2010, 34(14): 70-74.

[13] 马智泉, 李鹏, 王魁. 混沌粒子群优化投影寻踪法在电能质量监测网中的应用[J]. 水电能源科学, 2012, 30(5): 184-181.

Ma Zhiquan, Li Peng, Wang Kui. Application of chaotic particle swarm optimization and projection pursuit in power quality monitoring platform[J]. Water Resources and Power, 2012, 30(5): 184-181.

[14] 李志刚, 李玲玲. 串联系统的可靠性评估方法[J].电工技术学报, 2011, 26(1): 146-153.

Li Zhigang, Li Lingling. A method of evaluating the reliability of series systems[J]. Transactions of China Electrotechnical Society, 2011, 26(1): 146-153

[15] 刘冀, 王本德. 基于组合权重的模糊可变模型及在防洪风险评价中应用[J]. 大连理工大学学报, 2009, 49(2): 272-275.

Liu Ji, Wang Bende. Variable fuzzy model based on combined weights and its application to risk assessment for flood control engineering[J]. Journal of Dalian University of Technology, 2009, 49(2): 272-275.

Power Quality Comprehensive Evaluation Based on Matter-Element Theory and Evidence Theory

Li Lingling1,2 Liu Jingjie2 Ling Yuesheng1,2 Zhou Xian2 Zhang Yunlong2
（1. Hebei Province Ministry Joint Key Laboratory of Electromagnetic Field & Electrical Apparatus Reliability Hebei University of Technology Tianjin 300130 China 2. Electrical Engineering & Automation Tianjin University Tianjin 300072 China）

In order to solve the uncertainty and subjectivity of power quality comprehensive evaluation, an power quality comprehensive evaluation method is proposed based on matter-element theory and evidence theory in the paper. it use matter-element to establish matter-element model of power quality, it quantifies the subordinate relation of various evaluation indexes and evaluation interval of quality grades by correlation function, and normalizes it to obtain the belief function of each index. Then the weight of each evaluation index of power quality is obtained by using combination weighing method based on entropy weight and G1 method, to modify belef functions of the original evidence. on this basis, using evidence combination rule fuses various evaluation indexes, so as to obtain power quality comprehensive assessment. The calculation of an example shows that the proposed method minimizes the uncertainty in assessment process, can get more.

Power quality, matter-element theory, evidence theory, comprehensive evaluation

TM732

李玲玲 女，1968年生，博士，教授，博士生导师，研究方向为电力系统及其电器可靠性。

河北省科技支撑计划项目（12212173和13212104）；河北省建设科技研究计划项目（2011-147）；河北省高等学校创新团队领军人才培育计划项目（LJRC003）。

2013-08-06 改稿日期 2013-09-17

刘敬杰 女，1985年生，硕士研究生，研究方向为电器可靠性。