基于聚类的阶段理论线损快速计算与分析

李学平 刘怡然,2 卢志刚 鲍 锋

基于聚类的阶段理论线损快速计算与分析

李学平1刘怡然1,2卢志刚1鲍 锋3

（1. 燕山大学电力电子节能与传动控制河北省重点实验室 秦皇岛 066004 2. 国网冀北电力有限公司青龙县供电分公司 秦皇岛 066500 3. 国网黑龙江省电力有限公司 哈尔滨 150090）

针对自动采集数据缺失及单一断面网损无法刻画电网长期运行的情况，在仅考虑节点注入功率与网络参数变化的基础上，提出一种基于断面聚类的阶段理论线损快速计算与分析方法。本文首先对断面网损的构成进行了分析；其次针对断面数据采集情况提取断面特征向量，并且在数据采集不完整时，提出一种基于粗糙集理论的核特征向量求取方法；通过量化节点注入功率与网络参数单位变化引起的网损增量计算出与特征向量匹配的聚类中心断面的权系数向量；最后利用改进的最近邻聚类对断面进行聚类分析，快速得出任意时刻理论线损值和阶段理论线损值。Matlab仿真结果验证了此方法的有效性。

最近邻聚类 阶段理论线损 特征向量 相似度

1 引言

网损是衡量和考核供电企业生产经营的一项重要指标，理论线损与统计线损进行对比分析是考核线损管理程度的重要手段[1]。目前，利用某一时间断面或者典型日下的理论线损计算结果与统计线损进行对比分析得到的结果显然不够精确，不足以刻画电网长期的运行情况，所以能表述电网长时间运行的阶段理论线损的计算与分析有助于准确分析电网运行情况，为电网运行、生计和改造提供更为有价值的参考。

目前，国内外学者主要针对传统潮流计算方法的改进[2-3]、智能化算法的引进[4-5]以及基于数据自动采集平台[6]的理论线损计算等几方面对断面网损计算进行了研究，但是理论计算迭代时间长，并且在实际数据采集过程中，自动采集装置会有采集不成功的问题，使数据量通常达不到进行理论计算的数据需求；现有的网损费用分摊方法尽管是针对网损功率的，其原则也可用于实时及阶段网损电量的分摊，如比例分摊[7]，潮流跟踪分摊[8]或按电流分摊[9-11]，泰勒公式分摊等。但是，诸分摊方法中不同点在于对功率损耗中交叉项的处理不同，多采用人工指定比例因子法，缺乏精确的理论依据[12]。除此之外，对于网损的波动，文献[13]基于电路理论研究了发电权交易对网损的影响，文献[14]研究了基于灵敏度的网络参数变化对线损的影响，但都只是基于一个断面的分析，对实际指导意义不大。

随着电网中电能量采集系统的不断完善，自动采集装置采集频度的不断提高，数据库中的数据量越来越多，但数据采集的不完整将会使不间断实时理论计算耗费大量的时间及人力。因此聚类分析[15-16]成为处理大数据的一个研究热点。它通过选取合适的特征向量和相似度度量方法，可将大量数据分成多个具有相同性质的聚类簇，简化数据的处理和分析。

针对上述情况，在仅考虑节点注入功率与网络参数变化的基础上，本文提出一种基于聚类的阶段性理论线损计算与分析方法。首先利用电流叠加法对断面网损构成进行分析，得到节点注入功率与网络参数变化对网损影响的表达式。在数据采集完整时，根据网络参数变化情况提取不同断面的特征向量，在数据采集不完整时，提出一种基于粗糙集理论[18]的核特征向量求取方法；量化节点注入功率与网络参数单位变化引起的网损增量并计算出与特征向量匹配的聚类中心断面权系数向量；在此基础上利用一种改进的最近邻聚类法对任意时间段内的断面自动进行分类，利用聚类结果可快速得出任意时刻断面与阶段理论线损值，对网损的波动原因进行分析。

2 断面网损影响因素分析

电网在月度运行时，会在多种运行方式之间进行切换，在不同的运行方式下，电网络模型不相同。因此，需要对月度的电网进行分阶段分析，将相似和相同运行方式时的状态一起进行分析。在仅考虑节点注入功率与网络参数变化基础上进行如下分析。

2.1电网络模型

设电网络中有n个节点、q个电源。将电源等效为电流源（负荷等效为负的电流源），记为Iks。电网络的节点电压方程[11]可表示为

同理，从上式可得节点电压为

式中，Zim为网络中节点阻抗矩阵的解。

设网络中支路l的首端节点为i，末端节点为j，线路的导纳为yij=-Yij，阻抗为zij=1/yij≠Zij，支路l上的功率损耗[11]为

式中，i=1,2,…,n;j=1,2,…,n 。

2.2断面网损波动分析

2.2.1 节点注入功率波动影响分析

随着负荷的不断变化，不同断面中同一节点对网损的影响程度也不尽相同。在网架结构和网络参数不变时，各断面收敛电压波动十分微小，近似认为注入功率波动与注入电流波动呈线性关系。假设节点电流源k的注入功率变化引起的节点注入电流波动量为skIΔ˙。

由式（3）可得当电源节点k注入功率变化引起的支路l网损变化因子δkl为

电源k引起的全网网损波动量δk为

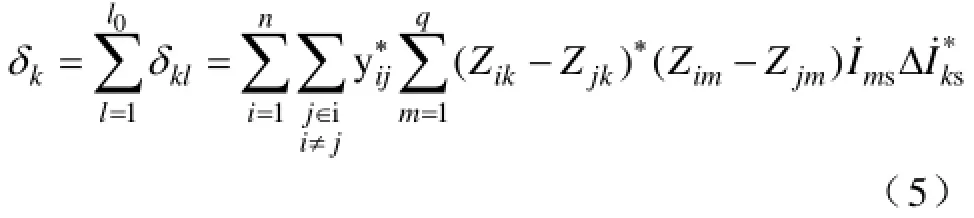
2.2.2 网络参数变化影响分析

网络参数的改变会导致电压的改变和潮流的重新分布，进而使全网网损发生变化。假设各电源的出力不变，支路l中的网络参数由yij变化为yi′j。采用文献[13]的方法求取参数变化引起的各节点电压变化向量ΔU˙，并设κi=ΔUi/Ui，从而求取引起节点注入电流变化量ΔI˙ls

节点k的注入电流为

支路l网络导纳参数变化引起全网网损波动量βl为

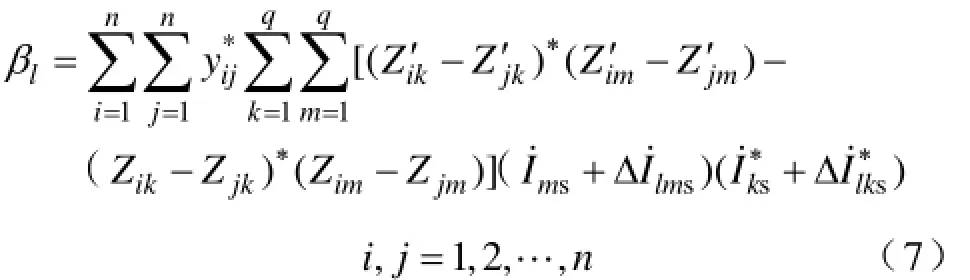
式中，imZ′为网络中支路l网络参数变化后新的节点阻抗矩阵中的元素。

3 断面相似性度量

本文利用聚类算法对断面进行聚类分析，首先定义几个概念:

（1）中心断面。指通过最近邻聚类得到的各聚类簇内的中心样本。

（2）实时断面。指当前正在进行聚类的断面样本。

3.1断面特征向量

考虑电网各节点负荷与网络参数在不同断面的变化特性和对不同断面的网损影响，定义节点采集情况向量A=(a1,a2,…,aq)，A为0、1离散向量，0代表采集失败，1代表采集成功。依据实时断面数据采集情况，则可提取出不同断面的特征向量。

（1）对于数据采集完整的断面（A为单位向量，任意ai≠0），在网络参数不发生变化时，将各电源节点的注入功率作为特征向量C=Cs=(c1s,c2s,…,cqs)；当网络参数发生变化时，则将节点注入功率特征向量Cs=(c1s,c2s,…,cqs)与网络参数特征向量Cl=(cy1, cy2,…,cyl0)组合为特征向量CB=Cs+Cl=(c1s,c2s,…, cqs,cy1,cy2,…,cyl0)。

（2）对于数据采集缺失的断面（A中任意ai=0），利用粗糙集理论[18]，利用此断面之前的数据采集完整断面的聚类中心结果作为决策属性D并构造信息系统S，逐一去除断面的特征向量C中的第i（i=1,2,…,q）个属性，并将其作为条件属性P，利用P重新聚类，并计算约减后条件属性对于决策属性的依赖度r(P, D)，从而找到一个相对最小的约减节点注入核特征向量集，使r(P, D)= r(C, D)；如果之前无数据采集完整断面的聚类中心结果，则默认核特征向量集P=C。

如果采集数据可匹配已存在的核向量，即断面数据采集成功节点集包含某个核特征向量CH所需节点集。则在网络参数不发生变化时，数据采集缺失断面的核特征向量为CH=(c1s,c2s,…,chs)，h≤q为约减后核特征向量中所需注入节点数；在网络参数发生变化时，将节点注入核特征向量CH=(c1s,c2s,…, chs)与网络参数特征向量C1=(cy1,cy2,…,cyl0)组合为核特征向量CHB=(c1s,c2s,…,chs, cy1,cy2,…,cyl0)；如果无采集数据匹配已存在的核向量，则省略此步骤，在聚类分析时针对此种情况特殊处理。

3.2权系数向量

节点注入功率与网络参数的变化对网损均有影响，不同的节点注入与不同网络参数变化对网损的影响也各不相同。本文通过权系数向量量化其对网损影响的不同程度。

通过式（5）和式（7）分别求取中心断面各节点注入功率单位波动时的网损增量ΔδM-i及网络参数单位变化时的网损增量ΔδM-l，M=1,2,…, Mlei，假设数据库中已存在类数为Mlei。根据数据采集情况的不同，则需利用ΔδM-i与ΔδM-l在所有中心断面中计算与实时断面特征向量匹配的中心断面权系数向量。

（1）当实时断面的数据采集完整、网络参数不变时，各中心断面权系数向量为wM=(wM-1, wM-2,…, wM-q)；且

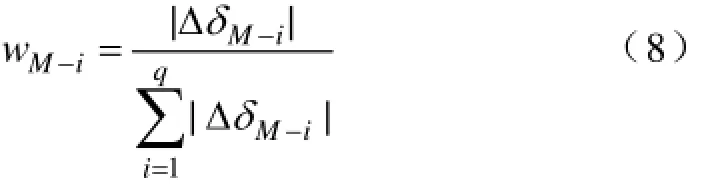
网络参数改变时，定义相对参数变化向量BM= (bM-1,bM-2,…,bM-l0), M=1,2,…, Mlei。BM为0，1离散向量，0代表实时断面相对中心断面参数不变化，1代表实时断面相对中心断面参数变化，各中心断面权系数向量由注入功率权系数与网络参数权系数两部分组成。wM-i＞0，wM-yi＞0，M=1,2,…, Mlei。

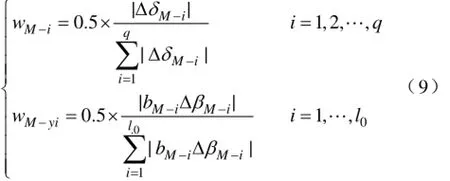
（2）同理，当实时断面的数据采集缺失时，如果此实时断面采集数据与约减后的某个核特征向量数据相匹配:在网络参数不变时，将式（8）中的q转换成核特征向量中所需注入节点数h可得各中心断面核权系数向量wHM=(wM-1, wM-2,…, wM-h)；当网络参数改变时，同样定义相对参数变化向量BM= (bM-1, bM-2,…, bM-l0)，将式（9）中的q转换成核特征向量中所需注入节点数h可得由核注入权系数与参数权系数两部分组成的各聚类中心断面核权系数向量wHBM=(wM-1, wM-2,…,wM-q,wM-y1,…,wM-yl0)。

（3）如果无采集数据匹配已存在的核向量，则省略此步骤，在聚类时针对此种情况特殊处理。

3.3断面相似度

断面采集数据属于典型的纵向数据，比较两个纵向数据项或数据序列的相似性一般采用基于距离度量的方法[17]。本文选取欧氏距离度量断面样本间的相似度，距离越小，相似度越大，反之亦然。

根据实时断面的数据采集与网络参数变化情况，在上文提取了合适的断面特征向量并求取与之相匹配的权系数向量的基础上，采取了不同的计算方法度量此实时断面与各中心断面的相似度，并通过相似度的比较找出与实时断面匹配的最近邻聚类。

（1）实时断面数据采集完整且参数不变，即

式中，l0为支路数，

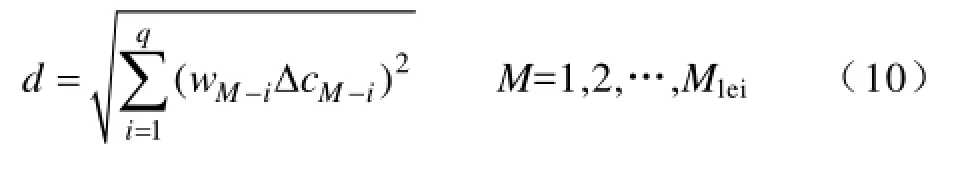
（2）实时断面数据采集完整且参数变化，即

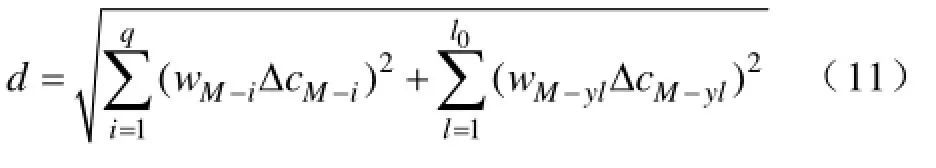
（3）实时断面数据采集缺失且参数不变，即

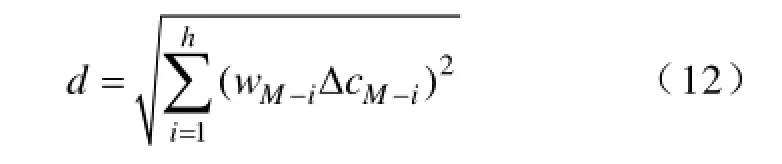
（4）实时断面数据采集缺失且参数变化，即

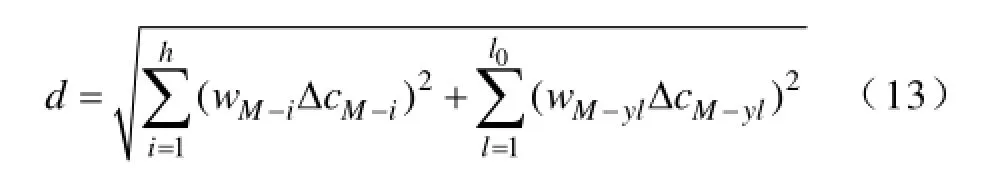
4 基于改进最近邻聚类的网损计算

4.1改进最近邻聚类法

最近邻聚类法是一种应用十分广泛的聚类算法，其利用样本的特征向量将多个样本自动分为不同的聚类簇，简便易行，但同时存在对某些聚类边缘的数据归属不清的问题。假设已存在m个聚类中心，算法不能处理m个类中的某些样本有可能与m类之后的某个聚类中心更为接近的情况。

针对上述聚类时对归属模糊的样本处理不完善的情况，提出一种通过提取各聚类簇中的局部最异点[19]进行二次聚类的改进的最近邻聚类算法。

4.2动态阈值的选取

聚类的个数与聚类簇内的样本数目主要取决于阈值，根据不同的精度需求和网架结构可选取不同的阈值。同一组样本，选取不同的阈值聚类结果也不尽相同。阈值越小，聚类簇内的网损波动越小，聚类结果越精确，但如果样本数量大，随着类数的增多，聚类速度也会减慢。

由于不同断面中各节点与支路对网损影响的权重不同，本文提出一种随着不同中心断面而变化的动态阈值概念。假设类中各节点允许的注入功率波动百分率范围为±a%，参数允许波动范围百分率为±b%，则参数不变情况下实时断面与第M类中心断面的阈值dM为

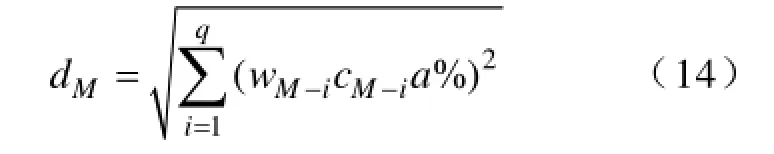
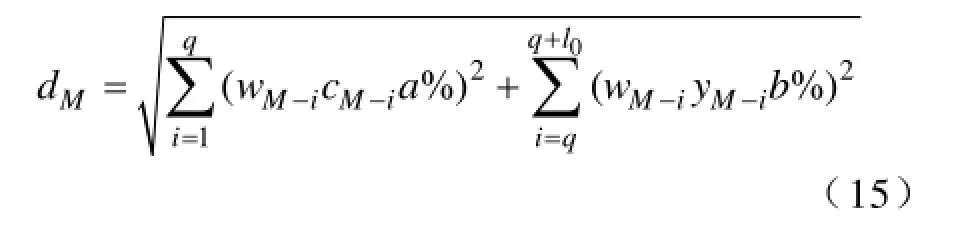
参数变化时的动态阈值dM为式中，M=1,2,…,Mlei，wM-i为第M类中节点i的权重。

在实际运行时，根据不同的电网实际运行情况的不同，选择一个符合实际的、合适的各节点允许的注入功率波动百分率与参数允许波动范围百分率，从而自动计算出合适的动态阈值。

4.3特殊情况的处理

如果采集数据不匹配任一核特征向量，则结合A计算数据缺失断面与数据库中心样本的相关系数ξlk及相似度，并按相关系数及相似度匹配规则确定聚类结果。相关系数匹配规则为将ξlk＞0.8的中心断面均作为此数据缺失断面的相似断面，并分别与其计算相似度。如果ξlk均小于0.8，则值班人员利用手动补全数据之后再次聚类。相似度匹配原则按照最近邻聚类的特点，取相似度最大为所属类。

相关系数计算式为

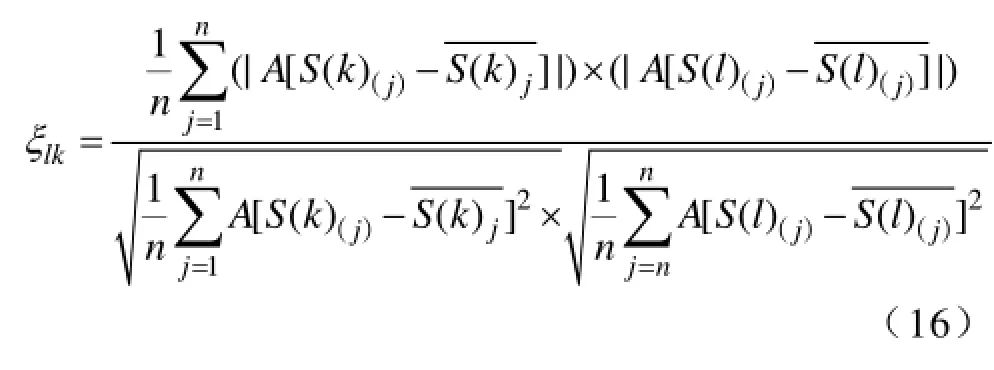
式中，S(k)(j)为数据完整时刻数据库中心时刻k的j节点的注入功率；S(k)(j)为数据完整时刻数据库中心时刻k节点注入功率均值；S(l)(j)为数据缺失时刻数据库中l时刻j节点的注入功率；S(l)(j)为数据缺失时刻数据库中l时刻节点注入功率均值。

相似度计算式为

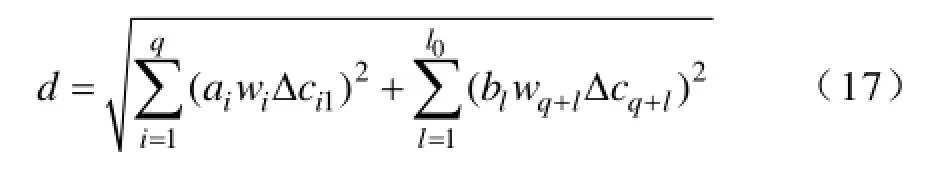
4.4断面聚类与网损计算

将每一个断面作为一个样本即聚类对象Xi，当有m个断面参与分析计算时，聚类的整个样本集为X=｛X1,X2,…,Xm｝，m为聚类对象的个数。

按照上述方法提取断面数字特征并比较断面相似度，利用改进的最近邻聚类方法对断面进行聚类分析。流程图如图1所示。最终确定W个聚类中心，计算每一类中样本的个数ki(i=1,2,…,W)；计算阶段理论线损值，计算式为

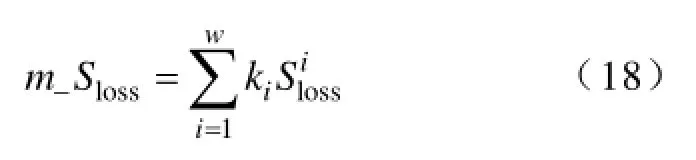
图1 断面聚类流程图Fig1 The flowchart of section clustering

4.5电网不同运行方式变化情况的处理

在不同的运行方式下，如果电网络的拓扑连接结构发生变化，其断面特征向量及其权系数向量的维数及大小都会发生相应的变化。因此，将不同运行方式下的聚类数据分别存储。在实际应用过程中，如果运行方式发生变化，首先搜寻数据库中有无相应运行方式的数据，如有，则在原数据基础之上进行计算，并将相同或相似方式下的结果进行统一的聚类分析即可；若无，则可将不同的运行方式作为新的时间阶段，从头开始重新计算。如果电网改造或规模扩展，则也将其视为一个新的时间阶段，权系数向量需要重新计算，其初值由最近邻聚类确定的第一个中心断面（即第一个样本）的理论计算结果得到。同时，各分阶段之间的数据融合与交互问题也是作者下一步研究的重点问题。

5 算例仿真与分析

选取IEEE14节点标准算例进行仿真，并利用某地实际发电厂和负荷出力波动曲线模拟某月内的节点注入功率波动情况。假设采集时间间隔Δt=1h，聚类结果如下。

5.124时刻采集完整断面聚类结果

24时刻不缺数据且网络参数不发生变化时的聚类结果与计算出的总损失结果如表1所示。由表1可知，利用聚类方法自动将一天24个断面分为10类，利用中心网损拟合的聚类簇中损失与实际利用理论线损计算程序得出的网损值大小非常接近，其最大误差为2.63%，全天损失拟合值与实际值的误差为-0.28%，其误差范围非常小。最后得到的拟合线损率与实际线损率的值也十分接近。

同时，由于支路1-2对网损的灵敏度最大，假设在14点以后支路1-2参数发生变化。聚类结果与损失计算结果见表2，从表2可知，参数改变后聚类结果明显增多。15点以后重新开始聚类，与14点前的中心作比较但聚类结果并未与其混淆，证明本文方法能有效的区分网络参数变化对断面网损产生的影响。由聚类结果得到的总网损误差非常小，拟合网损率与实际网损率差值同样相差不大。

表1 24时刻参数不变聚类结果Tab.1 The clustering results of 24 times with invariant parameters

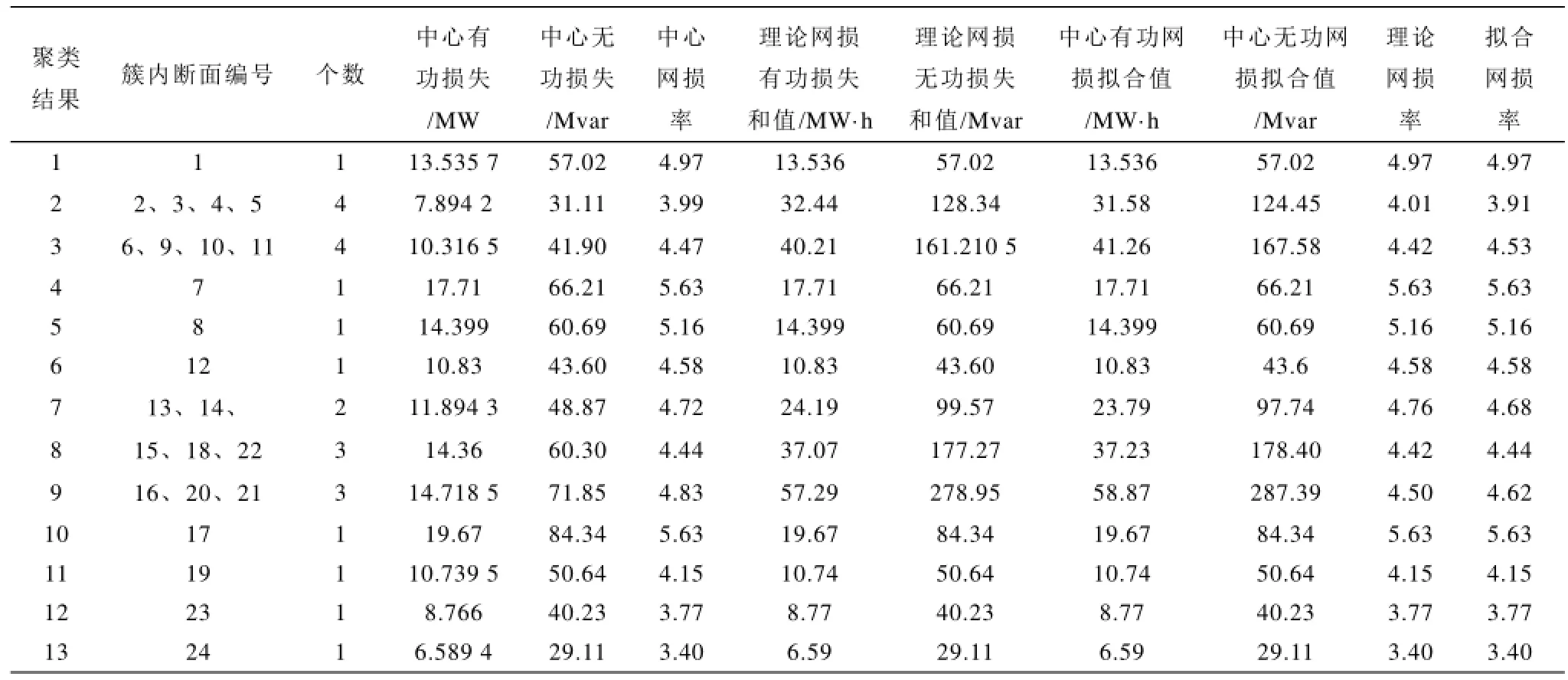
表2 24点参数变化聚类结果Tab.2 The clustering results of 24 times with varied parameters

5.2约减属性集与实时聚类

当遇到数据缺失的实时断面，则利用之前数据采集完整时的聚类结果构造信息系统，根据步骤，依次去除各节点的采集值，利用缺失属性的数据进行聚类，依据求取的条件属性依赖度进行属性约减。假设在24时聚类之后，另外出现三种不同数据缺失情况的断面。各断面缺失数据情况如表3所示，表中0代表此节点数据无采集，1代表此节点数据有采集。

表3 数据缺失情况表Tab.3 The table of missing date

用前文提到的粗糙集理论核约减，约减后相对约减核属性为{1, 2, 3, 6}，依据约减核属性进可对前24个数据进行准确分类。三种不同数据缺失情况断面的聚类结果如表4所示。

表4 不同情况缺数据实时断面聚类结果Tab.4 The real-time clustering results of different missing data

利用完整数据聚类则可知该断面属于第1类，在缺失数据情况下:断面1采集数据集包含约减核属性，则利用约减后的核属性将其聚到第一类，与完整数据聚类结果相符；断面2不包含约减核属性，因此根据其与中心断面的相关系数及相似度匹配原则进行分类，与其相关系数大于0.8的中心断面有1，7，8，15，其与1，7，8，15的距离分别为4.761 5、7.760 3、6.423 8，7.367 1，可以看出其与断面1距离最小，最为相似，将其归为第1类；断面3不包含约减核属性且其与所有已存在的中心断面相关系数均小于0.8，因此其不能进行准确分类，需进行人工补数再进行分类。

5.3阶段网损聚类结果

在上述基础上，依据某中等旅游城市7月份的负荷波动曲线模拟阶段内数据进行聚类分析，如图2所示。假设在此时间阶段内仅节点注入功率及支路和变压器参数发生变化，7月份属于该市气温最高的月份之一，随着温度的升高，游客的涌入，用电负荷将逐渐增加，到月底时基本达到全年气温最大值，网损也随之增加并逐步达到最大。

图2 阶段内日负荷波动曲线Fig.2 The phase fluctuation of load curve

全月共有744个断面，聚类结果如表5所示，由于篇幅限制，只显示聚类中心与类中样本数。由表5可知，总共将744个断面聚为23类，每个类中的个数各有不同。这同样证明了负荷波动的一般性和特殊性，即基本负荷波动不大，但是在月度间，会随时出现一些特殊的随机的负荷，致使负荷曲线波动较大，也造成了聚类结果中个数不尽相同，差距较大。类的中心增加趋势随着数据的增加逐渐放缓，如果数据达到一定的程度，数据库中将会包含所有类型的断面数据，实时计算结果会越来越准确。通过仿真计算相加和得到744断面的理论有功损失之和为10 748MW·h，无功损失为44 547Mvar，由改进最近邻聚类估算的阶段网损有功损失为10 628 MW·h，无功损失为44 558Mvar，证明了本方法计算结果与实际值的误差很小，通过聚类月度线损的计算准确率大大提高。

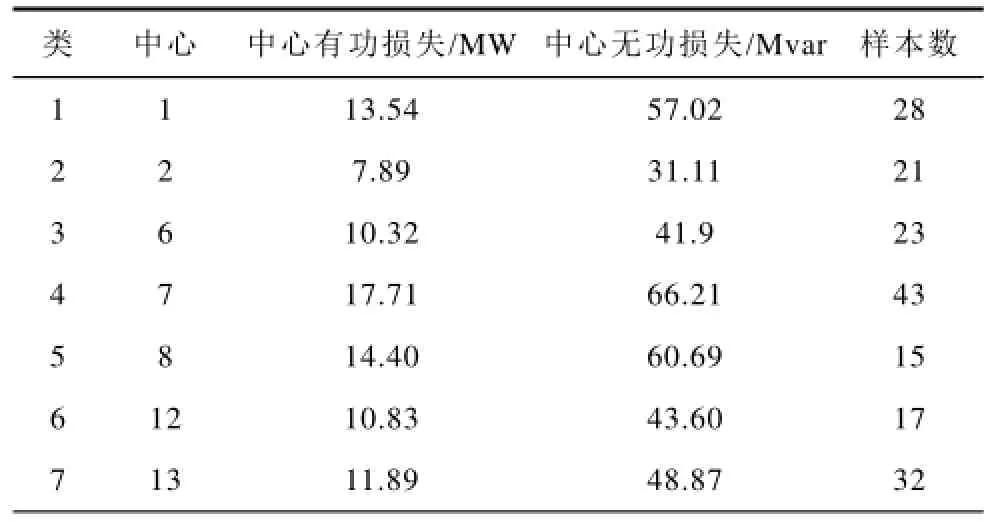
表5 阶段聚类结果Tab.5 The period of time clustering results

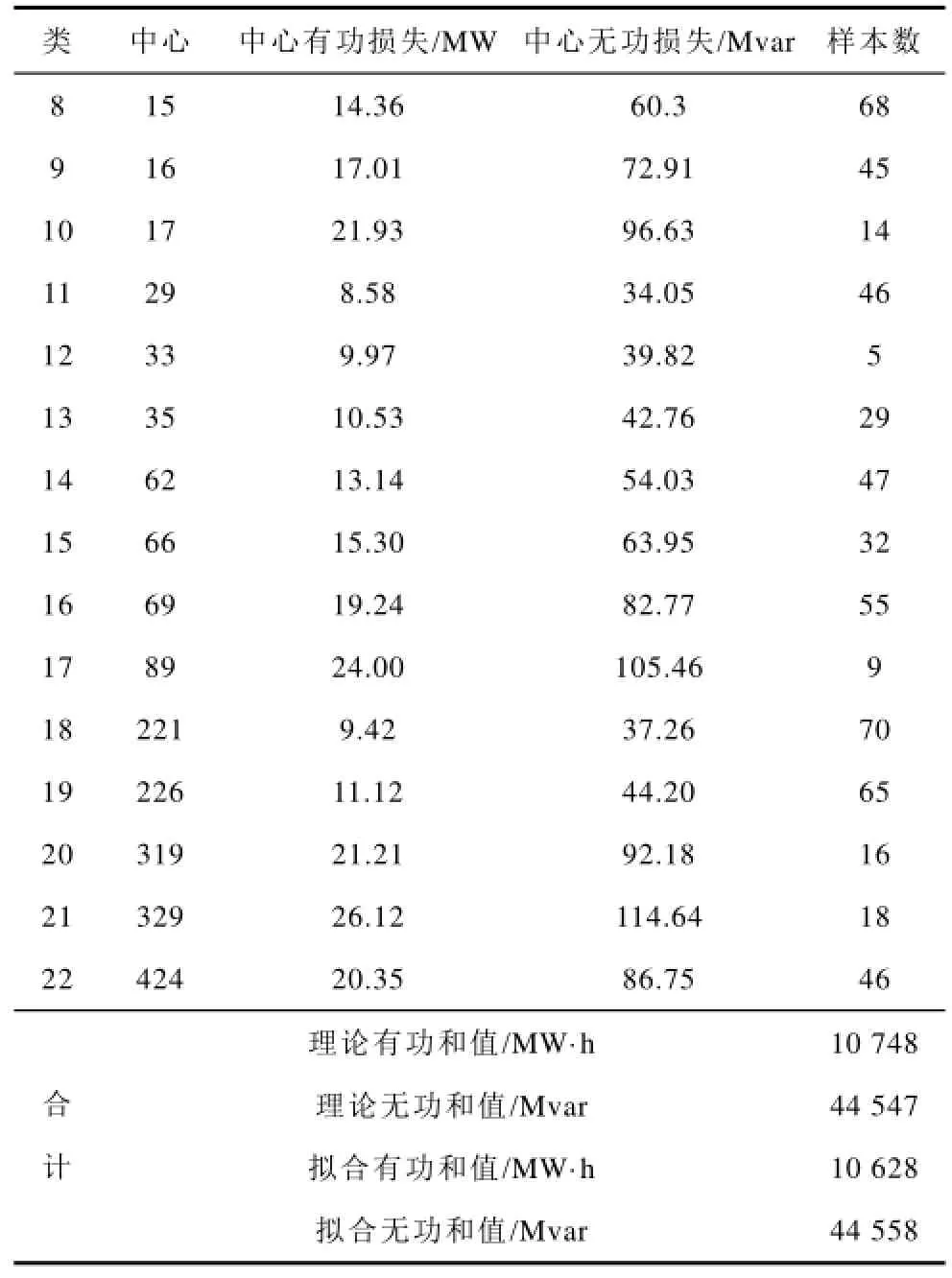
（续）

依据上述聚类结果得到的每日损失如表6所示，由表6可得图3所示的阶段内日损失对比曲线对比图。

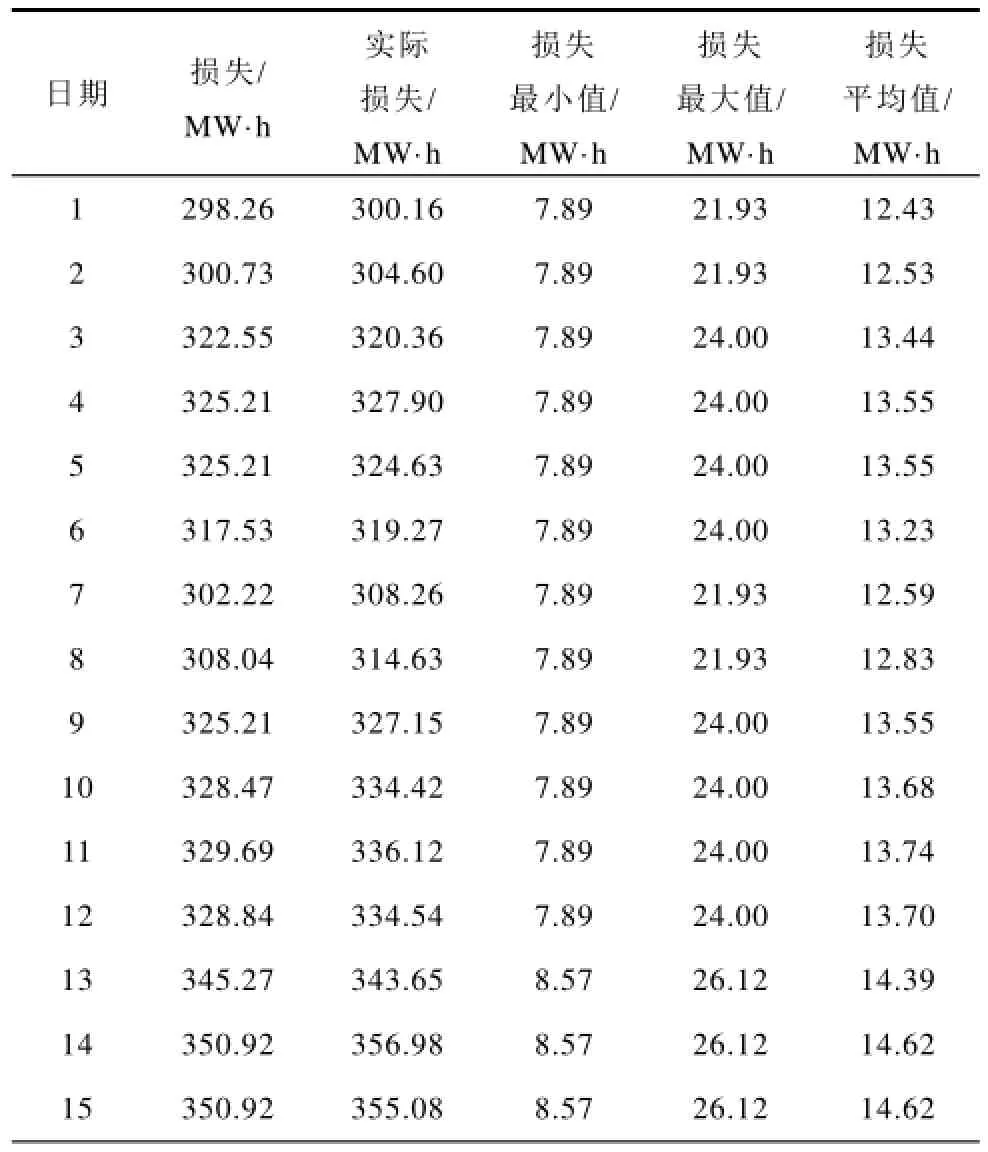
表6 阶段内每日网损结果Tab.6 The everyday clustering results in period of time

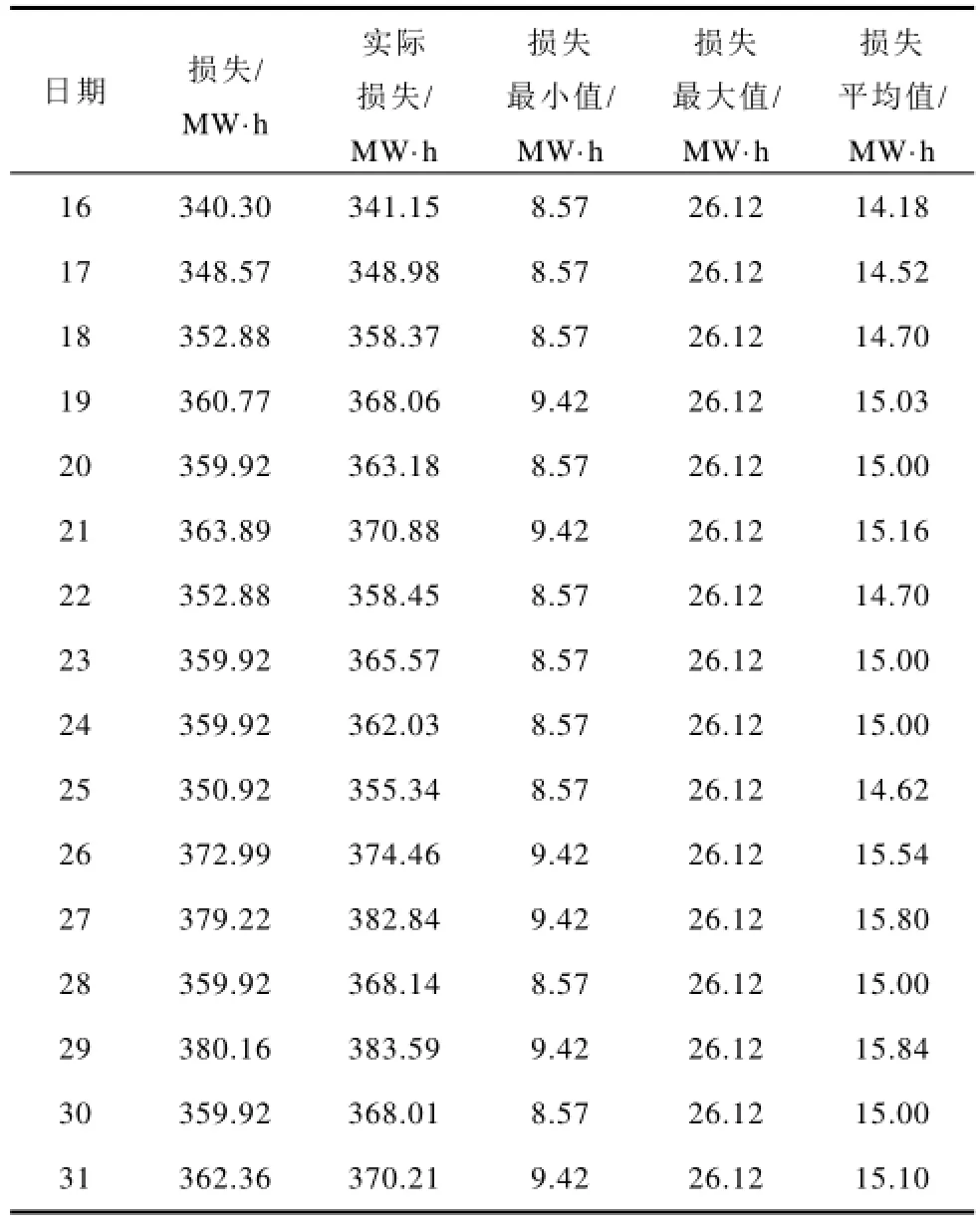
（续）

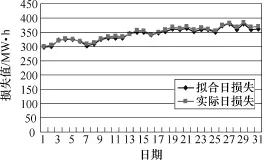
图3 阶段损失曲线波动对比图Fig.3 The comparison chart of phase loss curve wave

由图3可以看出，由聚类结果模拟的阶段有功波动曲线与实际的阶段损失波动曲线均十分相似，完全可以体现某一时间阶段内的损失波动趋势，并计算阶段内的损失电量。

具体分析可见，在1日～6日，气温偏低但天气以晴天为主，电网负荷相对波动较小呈缓慢上升趋势，网损值偏低；7日～8日，突然的降雨天气使负荷波动较大，网损值也呈较低趋势；9日～12日，气温较前几日有些升高，使得网损较前者略微升高；13日～18日，情况和第1类类似，此时间阶段内温度较为平稳，且温度在逐渐升高，天气以多云和阵雨为主，昼夜温差最大，因此此类的网损值较大。18日～25日，在天气情况和温度方面较前者相差不多，但因该城市属于旅游型城市，随着7月份旅游高峰季节的到来，用电量在前者基础上会有所上升，导致负荷增加，网损增大。7月25日开始，该地区进入一年中温度最高的时间阶段，天气闷热，空气湿度明显增大，人体的反应较为强烈，所以电网负荷会大幅提高，网损率也达到最大值。

6 结论

本文将最近邻聚类技术应用到阶段理论线损的近似计算当中，通过聚类既可以反映一定时间阶段内各个典型断面的负荷变化情况，也可以快速得到阶段网络损耗的值，减少了不间断计算每个代表日理论线损所带来的人力和物力资源的浪费，同时阶段理论线损对电网实际运行具有更实际的指导意义。并通过仿真结果验证了本文所提方法的可行性和有效性。

[1] 余卫国, 熊幼京, 周新风, 等. 电力网技术线损分析及降损对策[J]. 电网技术, 2006, 30(18): 38-42.

Yu Weiguo, Xiong Youjing, Zhou Xinfeng, et al. Analysison technical line losses of power grids and counter measures to reduce line losses[J]. Power System Technology, 2006, 30(18): 38-42.

[2] 余涛, 刘靖, 胡细兵. 基于分布式多步回溯Q(λ)学习的复杂电网最优潮流算法[J]. 电工技术学报, 2012, 27(4): 185-192.

Yu Tao, Liu Jing, Hu Xibing. Optimal power flow for complex power grid using distributed multi-step backtrack Q(λ)Learning[J]. Transactions of China Electrotechnical Society, 2012, 27(4): 185-192.

[3] 卢志刚, 程慧琳, 冯磊. 基于支路功率选取的功率扩展潮流计算[J]. 电工技术学报, 2013, 28(6): 208-214.

Lu Zhigang, Cheng Huilin, Feng Lei. Extended-power load flow calculation based on selection of branch power[J]. Transactions of China Electrotechnical Society, 2013, 28(6): 208-214.

[4] 李秀卿, 赵丽娜, 孟庆然, 等. IGA优化的神经网络计算配电网理论线损[J]. 电力系统及其自动化学报, 2009, 21(5): 87-91.

Li Xiuqing, Zhao Lina, Meng Qingran, et al. Calculation of line losses in distribution systems using artificial neural network aided by immune genetic algorithm[J]. Proceedings of the CSU-EPSA, 2009, 21(5): 87-91.

[5] 彭宇文, 刘克文. 基于改进核心向量机的配电网理论线损计算方法[J]. 中国电机工程学报, 2011, 31(34): 120-126.

Peng Yuwen, Liu Kewen. A distribution network theoretical line loss calculation method based on improved core vector machine[J]. Proceedings of the CSEE, 2011, 31(34): 120-126.

[6] 邓芳. 配网线损实时统计与分析系统[J]. 电网技术, 2007, 31(1): 186-188.

Deng Fang. Real time measurement and analysis system of line losses in distribution networks[J]. Power System Technology, 2007, 31(1): 186-188.

[7] Exposito G, Salltos J M R, Garcia T G, et al. Fair allocation on transmission power losses[J]. IEEE Trans on Power Systems, 2000, 15(L): 184-188.

[8] 徐昌凤. 改迸潮流跟踪法输电固定成本分摊的研究[D]. 南昌大学, 2012.

[9] 李春燕, 俞集辉, 谢开贵, 等. 基于扩展关联矩阵的电流跟踪模型和算法[J]. 电工技术学报, 2008, 23(4): 104-111.

Li Chunyan, Yu Jihui, Xie Kaigui, et al. Model and algorithm of current tracing based on extended incidence matrix[J]. Transactions of China Electrotechnical Society, 2008, 23(4): 104-111.

[10] 谭伦农, 张保会. 输电线路的利用份额及损耗分摊问题[J]. 电工技术学报, 2002, 17(6): 97-101.

Tan Lunnong, Zhang Baohui. Problems of using proportion of transmission line and loss allocation[J]. Transactions of China Electrotechnical Society, 2002, 17(6): 97-101.

[11] 颜丽, 鲍海. 基于电流分布的电网功率分布因子的计算[J]. 中国电机工程学报, 2011, 31(1): 80-85.

Yan Li, Bao Hai. Algorithm of power distribution factor based on current distribution[J]. Proceedings of the CSEE, 2011, 31(1): 80-85.

[12] Ai Dongping, Bao Hai, Yang Yihan. Analysis of loss compensation on generation rights trade by circuit theory[C]. Power and Energy Eng. Conf. (APPEEC), 2010: 1-4.

[13] 冯林桥, 许文玉, 刘飞. 实时网损电量的计算及分摊[J]. 中国电机工程学报, 2004, 24(2): 66-70.

Feng Linqiao, Xu Wenyu, Liu Fei. Calculation and apportionment of real-time electric energy loss in power network[J]. Proceedings of the CSEE, 2004, 24(2): 66-70.

[14] 卢志刚, 魏国华, 朱连波, 等. 线路损失的灵敏度分析和参数综合优化[J]. 高电压技术, 2010, 36(5): 1311-1316.

Lu Zhigang, Wei Guohua, Zhu Lianbo, et al. Sensitivity analysis of line losses and parameter’s comprehensive optimization[J]. High Voltage Engineering, 2010, 36(5): 1311-1316.

[15] 张绍德, 毛雪菲, 毛雪芹. 基于最邻近聚类支持向量机辨识的电弧炉逆电极控制[J]. 控制理论与应用, 2010, 27(7): 909-915.

Zhang Shaode, Mao Xuefei, Mao Xueqin. Inverse control for electrodes in electric are furnace based on support-vector-machines identification on nearest neighbor lustering[J]. Control Theory & Applications, 2010, 27(7): 909-915.

[16] 张秀玲, 宋建军, 褚福磊, 等. 基于动态最近邻聚类算法的RBF神经网络及其在MH-Ni电池容量预测中的应用[J]. 电工技术学报, 2005, 20(11): 84-87.

Zhang Xiuling, Song Jianjun, Chu Fulei, et al. RBF neural networks based on dynamic nearest neighborclustering algorithm and its application in prediction of MH-Ni battery capacity[J]. Transactions of China Electrotechnical Society, 2005, 20(11): 84-87.

[17] 李会民, 方丽英, 闰健卓, 等. 基于扩展范式距离的纵向数据相似性度量[J]. 计算机与应用化学, 2012, 29(10): 1176-1180.

Li Huimin, Fang Liying, Yan Jianzhuo, et al. Algorithm based on norm distance distance similarty measurement for longitudinal data[J]. Computers and Applied Chemisty, 2012, 29(10): 1176-1180.

[18] 邓冠男. 聚类分析中的相似度研究[J]. 东北电力大学学报, 2013, 33(1/2): 156-161.

Deng Guannan. The similarity measure in clustering [J]. Journal of Northeast Dianli University, 2013, 33(1/2): 156-161.

[19] 钱鹏江, 王士同, 邓赵红, 等. 基于最小包含球的大数据集快速谱聚类算法[J]. 电子学报, 2010, 38(9): 2035-2041.

Qian Pengjiang, Wang Shitong, Deng Zhaohong, et al. Fast spectral clustering for large data sets using minimal enclosing ball[J]. Acta Electronica Sinica, 2010, 38(9): 2035-2041.

Phase Theoretical Line Loss Calculation and Analysis Based on Clustering Theory

Automatic acquisition may fail to collect data; what’s more, single section network loss can not depict loss of power grid during a period. In view of the above facts, a method based on clustering theory for phase theoretical line loss calculation and analysis is proposed，which only takes node power injection and parameter variation into account. Firstly, the composition of section network loss is analyzed. Secondly, on the basis of section data, feature vector is extracted. A nuclear feature vector calculation method based on rough set theory is used to deal with the situation of failure acquisition. Weight vector of the clustering center section is calculated to match the feature vector through quantizing the network loss increment caused by node power injection and network parameters variation. Finally, the nearest neighbor clustering is improved to analyse and to obtain the theoretical line loss of any section and any period. The Matlab simulation results demonstrate the effectiveness of the proposed method.

Nearest neighbor clustering, phase theoretical line loss, feature vector, similarity measure

TM744

李学平 男，1976年生，博士，讲师，研究方向为电力系统经济运行与分析。

国家自然科学基金（61473246）、河北省自然科学基金（E2015203294）、中国博士后科学基金（2014M551049）资助项目。

2013-09-11 改稿日期 2013-12-07

Li Xueping1 Liu Yiran1,2 Lu Zhigang1 Bao Feng3

（1. Key Lab of Power Electronics for Energy Conservation and Motor Drive of Hebei Province Yanshan University Qinhuangdao 066004 China 2. State Grid Jibei Electric Power Company Limited Qinglong County Electric Power Supply Company Qinhuangdao 066500 China 3. State Grid Heilongjiang Province Electric Power Company Limited Haerbin 150090 China）

刘怡然 女，1986年生，硕士研究生，研究方向为电力系统线损计算与分析。