无电压传感PWM整流器的虚拟磁链自适应滑模观测研究

肖 雄 张勇军 王 京 李华德

无电压传感PWM整流器的虚拟磁链自适应滑模观测研究

肖 雄 张勇军 王 京 李华德

（北京科技大学冶金工程研究院 北京 100083）

针对无电压传感的三相PWM整流器虚拟磁链估计中存在直流偏置和初值等问题，本文提出一种具有自适应功能的新型虚拟磁链滑模观测与控制策略。该策略将滑模变结构控制引入虚拟磁链观测器中，以Sigmoid函数为切换函数估计出网侧电源电压值，根据理想磁链与虚拟电动势的正交关系设计了自适应控制率来动态调整磁链补偿基准，使其能够快速准确地跟踪网侧电压波动带来的磁链变化，实现实时检验和修正虚拟磁链值的作用。新型的虚拟磁链观测器合理减少了传感器的数量，同时提高了虚拟磁链的观测精度，将其应用于整流器DPC系统中，仿真和实验结果表明，新型无电压传感控制策略有效抑制了直流母线电压动态响应波动，更有利于滤除网侧电流谐波，改善电能质量。

PWM整流器 虚拟磁链 自适应滑模观测器 直接功率控制 无电压传感

1 引言

三相电压型PWM整流器具有单位功率因数、低输入电流谐波含量、能量可控双向流动等优点，近年来已成功应用在工业传动、风力发电等场合，受到广泛的关注[1-2]。尤其是近年来对可再生能源并网技术研究的持续升温，新型PWM整流器控制策略越来越成为了众多学者研究的热点。PWM整流器从矢量定向控制角度来说分为电网电压定向控制和虚拟磁链定向控制，从控制策略上可以分为传统的间接电流控制、直接电流电压的双闭环控制[3]、有功无功功率的直接控制[4-5]以及随着控制理论的发展所涌现出来的一些非线性控制策略[6-7]，方法的多样化也带来了系统各方面性能的提升。

PWM整流器是典型的非线性、时变不确定系统，虚拟磁链定向的矢量控制能有效抑制网侧谐波对基波矢量相位角的检测影响及网侧电压对矢量定向控制性能的影响[8]，所以对虚拟磁链的准确估计以及利用检测量观测处坐标系统的空间位置角是整流器虚拟磁链矢量定向控制系统良好运行的关键。传统的虚拟磁链估计存在的初值和直流偏置问题，文献[9]提出了带初值估计的磁链观测方法，将采样电流离散化，得到磁链初始值，有效的抑制了启动电流的冲击。文献[10]提出了改进的带饱和限幅反馈环节积分器的虚拟磁链观测器，稳态下效果较好，动态响应性能对参数依赖较多。文献[11]采用锁相环获取电网空间角度来与虚拟磁链相结合控制，该方法在电网电压跌落和电压不平衡时取得了较好的效果，在启动时波动较大有待改进。随着控制理论的发展，线性控制策略在处理相关控制问题时尚存在不足[12]，许多学者将非线性控制算法应用到整流器的控制中来解决问题，文献[13]提出软件锁相环与预测控制相结合的直接控制策略，提高了动态性能，解决了延时补偿问题。文献[14]对电网频率、感抗、幅值等系统参数采用遗传算法进行启动前辨识，以此估计出虚拟磁链值并对其初值进行精确观测，取得了良好的辨识效果。

由于滑模控制建模无需了解系统中各项参数，鲁棒性较强，对系统参数变化和扰动不敏感，在非线性控制系统中得到广泛应用。文献[15]与[16]将滑模控制引入整流器电流双闭环控制中，文献[17]将滑模控制与直接功率控制相结合，上述文献均针对传统的PI控制带来的滞后性和对系统参数的敏感性进行的改进。本文针对无电压传感的三相PWM整流器虚拟磁链估计中存在直流偏置和初值等问题，提出一种新型自适应滑模虚拟磁链观测器控制策略。该策略将滑模变结构控制引入虚拟磁链观测器中，运用滑模控制技术估计出网侧电源电压并积分出虚拟磁链，同时针对积分环节设计自适应补偿器进行磁链补偿。在此基础上对所提出的观测器进行仿真研究，并将其应用于整流器DPC系统中与传统的虚拟磁链无传感方案进行了仿真比较；最后在自主的整流器实验平台上进行了实验算法验证，仿真和实验结果验证了新型的PWM整流器无电压传感控制策略的可行性及有效性。

2 PWM整流器无电压传感DPC控制

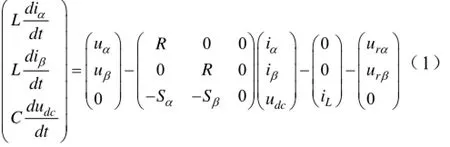
在两相静止αβ坐标系中，三相电压型PWM整流器数学模型可以表示为:式中，uα、uβ、iα、iβ为αβ坐标系下网侧相电压和网侧输入电流，L为网侧滤波电抗的电感值，R为开关管损耗等效电阻和滤波电感等效电阻合并总阻抗，C为直流侧电容，dcu为输出直流电压，Li为负载电流，Sα、Sβ为开关函数，ruα、ruβ为整流器输入相电压。

传统无电网电压传感器DPC控制采用了基于虚拟磁链定向的瞬时功率估计方案（VF-DPC），其结构如图1所示。VF-DPC控制中虚拟磁链估算为

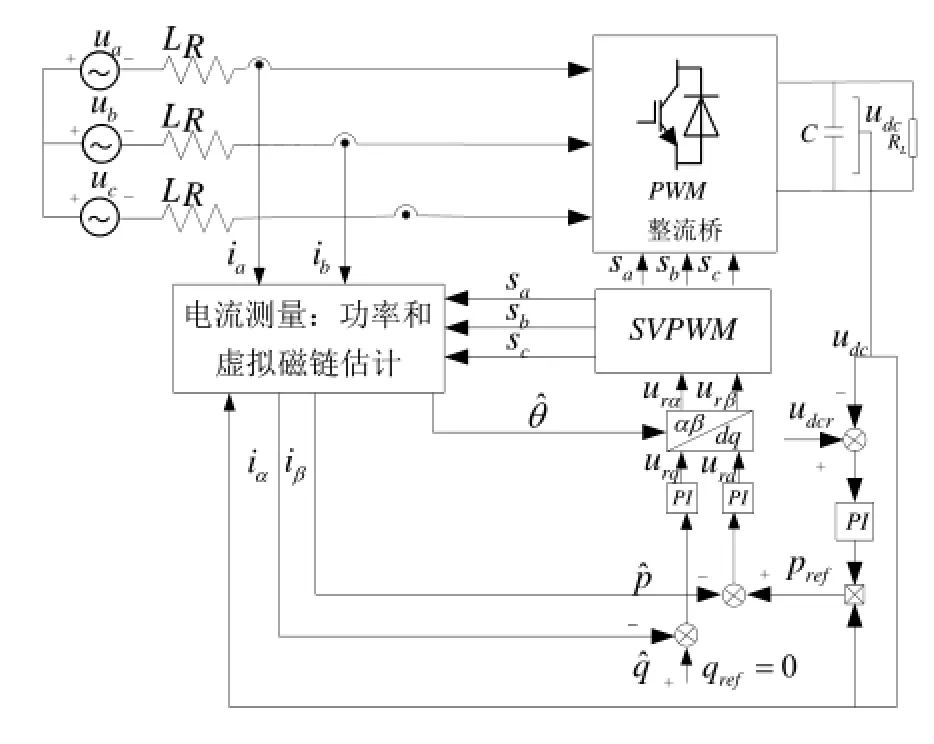
图1 传统无电压传感VF-DPC系统结构Fig.1 Block diagram of Traditional VF-DPC structure

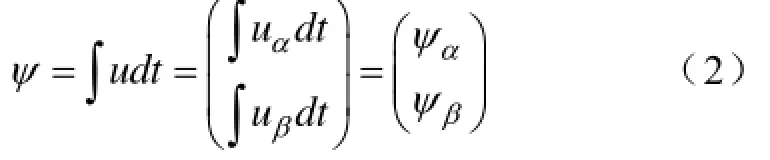
则有

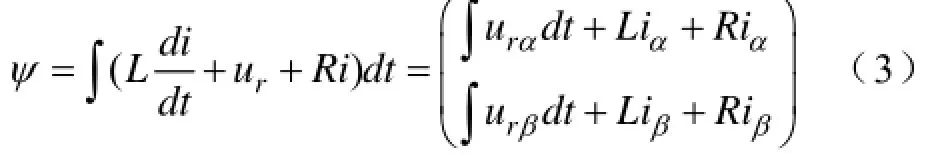
式中，

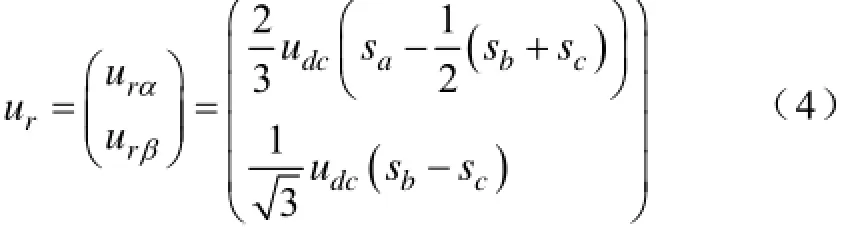
将检测得到的输出电流和估算出的虚拟磁链输入输入瞬态功率估算单元，根据ψ=ψα+jψβ及u= dψdt，磁链幅值恒定，可得有功功率p和无功功率q表达式为

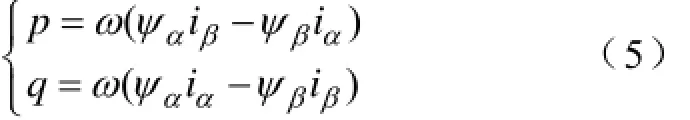
式中，ω为电网基波角频率，上式中电压、电流及磁链矢量关系如图2所示。

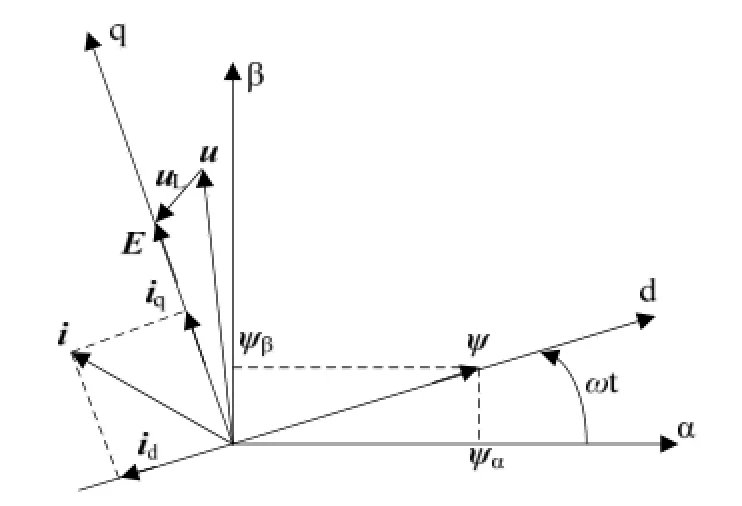
图2 电压、电流及磁链矢量关系图Fig.2 Voltage, current and flux vector diagram

3 自适应滑模观测器无电压传感DPC控制

针对传统的无电压传感中磁链估计存在积分初值和直流偏置等问题，同时为了降低THD，提高整流器DPC系统的动态性能，在原有的数学模型和虚拟磁链定向下的功率模型基础上，融入滑模控制技术进行磁链估算，并设计了自适应控制器来补偿磁链估计误差。

3.1虚拟磁链滑模观测器

本文设计用连续的可变边界层厚度的Sigmoid函数作为切换函数进行电压值估计。根据三相VSR在αβ静止坐标下的数学模型，由式(2) (3)可得

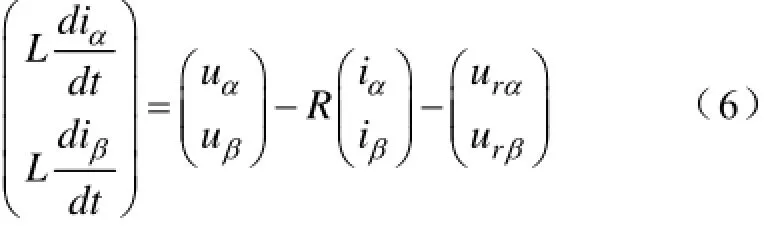
根据滑模变结构控制的基本理论，由式(6)可构造虚拟磁链滑模观测器:

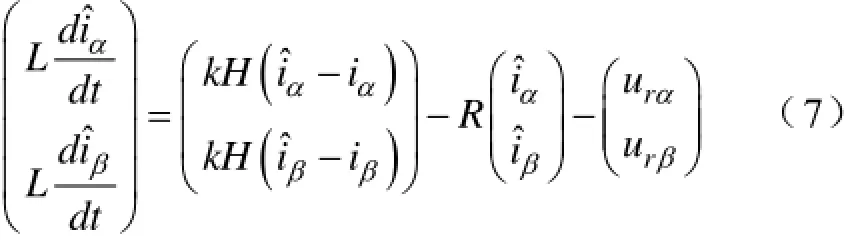
式中，k为滑模增益系数，（）Hx为Sigmoid函数，表示为:

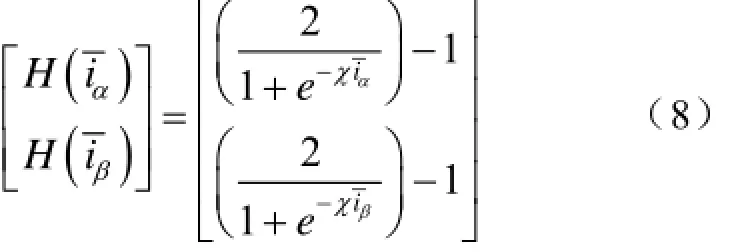
式中，χ为一个正数，用于函数的斜率的调节，图3为不同χ取值下的Sigmoid函数曲线图。

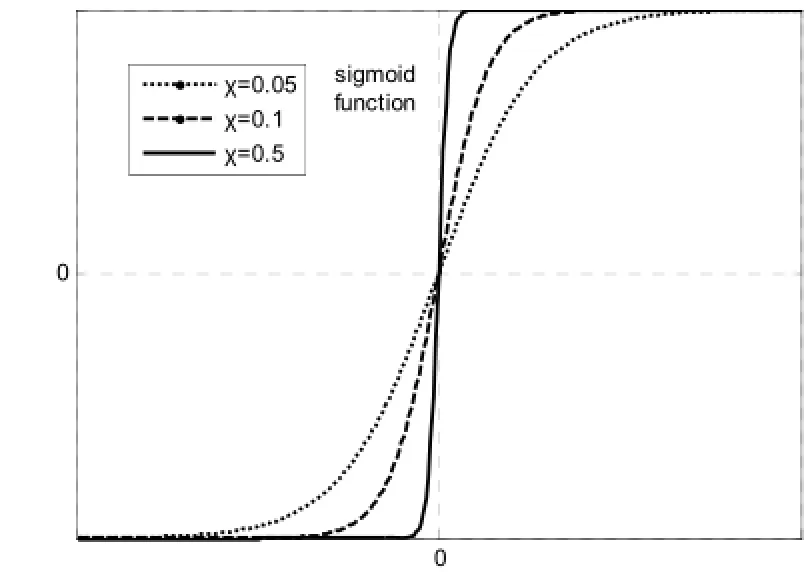
图3 Sigmoid函数曲线图Fig.3 The curve with Sigmoid functions

由式(6) (7)可得动态误差方程为

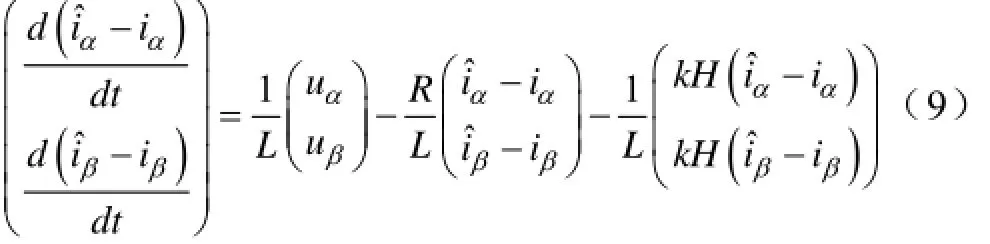
系统到达滑模面且在滑模面上运行时，H(x)= H˙(x)=0，即

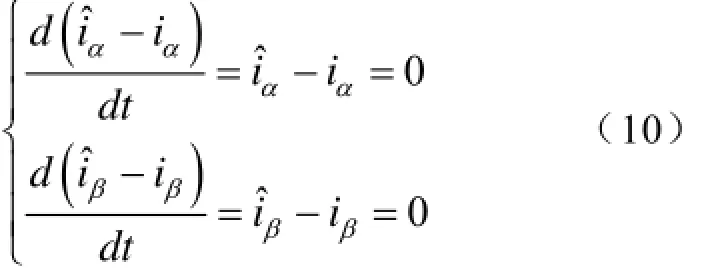
ur由式（4）给出，按照式（7）构建滑模观测器，当增益k满足系统的可达性条件时，系统将在有限时间内进入滑动模态。综合以上式子，则电网电压估计可以表示成:

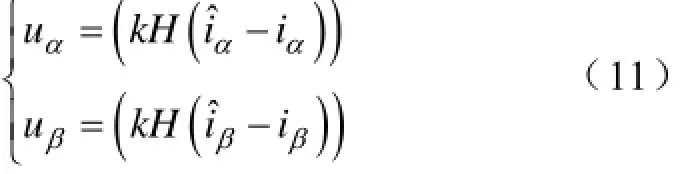
由式（8）和式（11）可得χ、k的取值关系

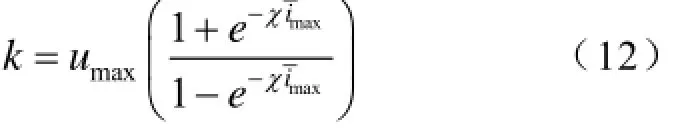
由式（2）则有虚拟磁链估计值为

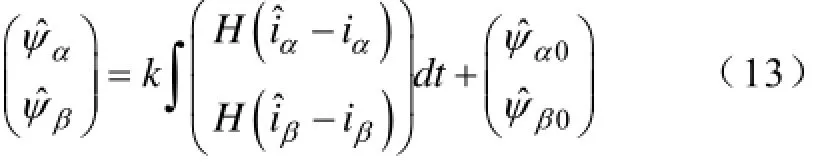
3.2自适应补偿控制

考虑到磁链估计积分环节中出现的初值、直流偏置以及电网电压不稳定会造成PWM整流器虚拟磁链幅值不恒定等问题，在理想磁链应和虚拟电动势处于完全正交关系的基础上，引入自适应控制器来调整磁链补偿基准，目的是使其快速地跟踪上网侧电压波动带来的磁链变化，及时校正虚拟磁链值。

依据积分器的通用形式，带有反馈补偿功能的虚拟磁链信号可以表示为

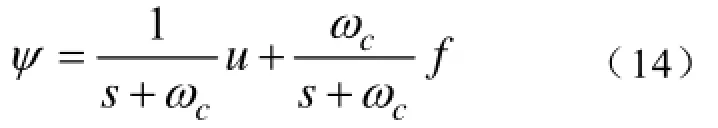
式中，ψ为虚拟磁链，作为输出；u为电源电压作为输入；f为反馈补偿信号，若为零则为低通滤波器，若为磁链幅值则为纯积分器，因此其取值的设计影响着观测器综合性能的优良。

理想情况下虚拟磁链矢量ψ比电网电压矢量u滞后90°，若因初始值、直流分量或者负载的突变等情况引起的正交关系被破坏，定义误差为:

令cosγλ=，这里称γ为正交补偿因子，λ为观测磁链向量ψ与向量u的夹角，eΔ作为PI调节器的输入信号，则补偿量为

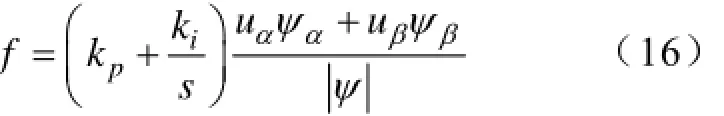
式中，分子部分为虚拟磁链和电网电压两向量点积，分母为两向量幅值数积，综合式（14～16），则有

图4为自适应补偿原理图。当λ＞90°，此时正交计算的结果γ＜0，即Δe＜0，PI调节器的输出就会减小，虚拟磁链反馈补偿量ψcmp的模减小，这样磁链的输出就会由向ψ逼近，ψ不变cmpLPF的情况下，直至向量ψ与向量u重新恢复正交的关系。同理，当两向量之间的夹角λ＜90°时，会使虚拟磁链反馈补偿量ψcmp的模增大，最终同样会使向量ψ与向量u恢复正交的关系。图5为依据以上原理建立的自适应控制器结构图

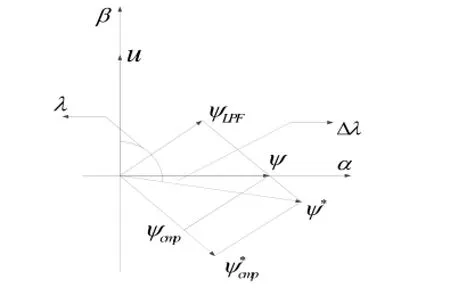
图4 自适应补偿原理图Fig.4 Block diagram of adaptive compensation principle

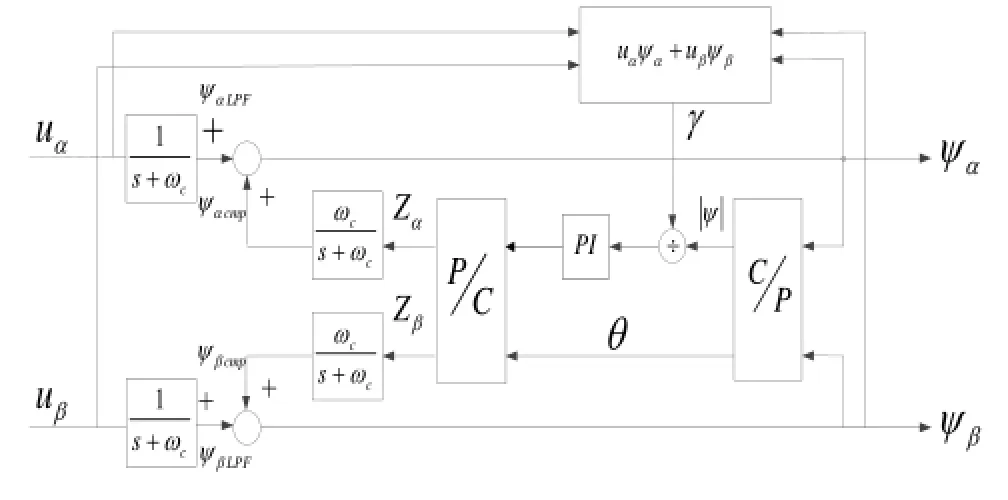
图5 自适应控制器结构图Fig.5 Block diagram of the adaptive controller structure

即可得虚拟磁链的位置

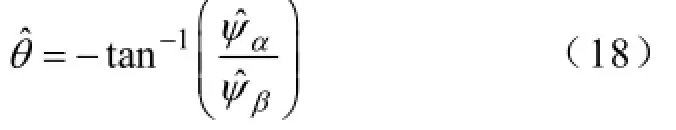
结合式(5)和补偿过后的虚拟磁链值，则可得有功功率p和无功功率q表达式为

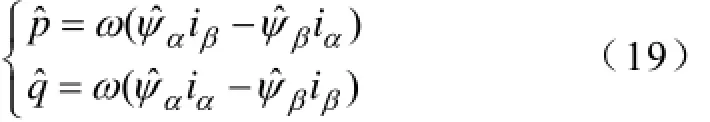
综合上述策略，得到自适应滑模观测器结构图如图6所示。

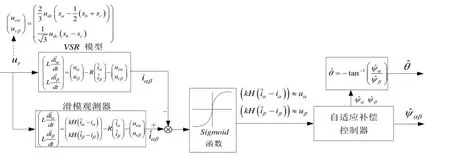
图6 自适应滑模观测器结构图Fig.6 Block diagram of the adaptive SMO based on sigmoid function

3.2综合控制策略

引入自适应滑模观测器控制策略，整个系统的结构图如图7所示。图中通过自适应滑模观测器对虚拟磁链进行估算，进而得到矢量位置角，通过对实际功率估算，与设定值进行比较，得到瞬时有功、无功功率的误差信号Δp、Δq，从而引入PI调节器并通过坐标变换得到相应的开关控制信号，实现了具有虚拟磁链自适应滑模观测的无电压传感DPC控制[18-19]。

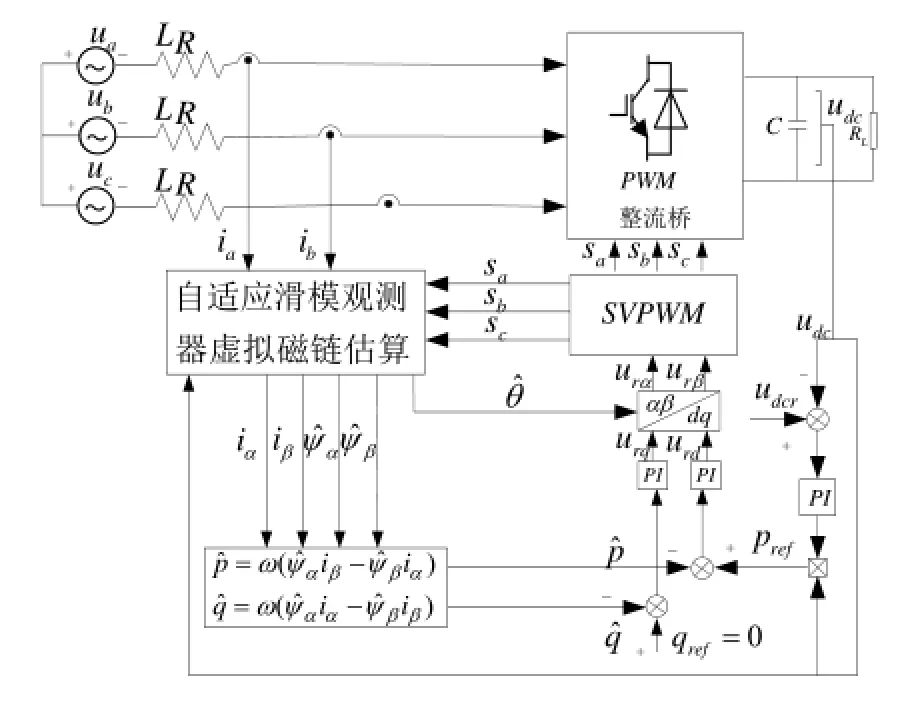
图7 虚拟磁链自适应滑模观测器直接功率控制结构图Fig.7 Block diagram of VF-DPC structure based on adaptive sliding mode observer

4 仿真与实验

4.1自适应滑模磁链观测器仿真

为了验证自适应滑模虚拟磁链观测器的可行性及有效性，在Matlab/Simulink环境下搭建了仿真模型，给定输入信号幅值为1，频率为2 rad/s的电压正弦波，系统中所有变量的初始值为0，并且截止频率设定为20rad/s。

图8为自适应滑模观测法、传统饱和抑制法、一阶低通滤波器和纯积分观测方法在稳态下所输出的曲线与理想曲线的波形对比；图9、10为饱和抑制和自适应滑模在动态下的波形对比，图9在8s时输入电压信号幅值设定变为2，频率为6rad/s，图10在6s时输入电压信号幅值设定变为0.3，频率为1rad/s。综合上述图可以看出，纯积分观测器会有初始值和直流分量带的偏移；一阶低通滤波器虽然抑制了直流偏移但是引起了幅值和相位误差；传统的饱和抑制和自适应滑模观测方法在稳态情况下，相对于纯积分观测器和一阶低通滤波器，均能取得比较理想的效果；动态时幅值和频率突变的情况下，饱和抑制很难做到有效的观测，而自适应滑模仍能够准确的跟踪到理想磁链，体现其良好的动态响应性能。

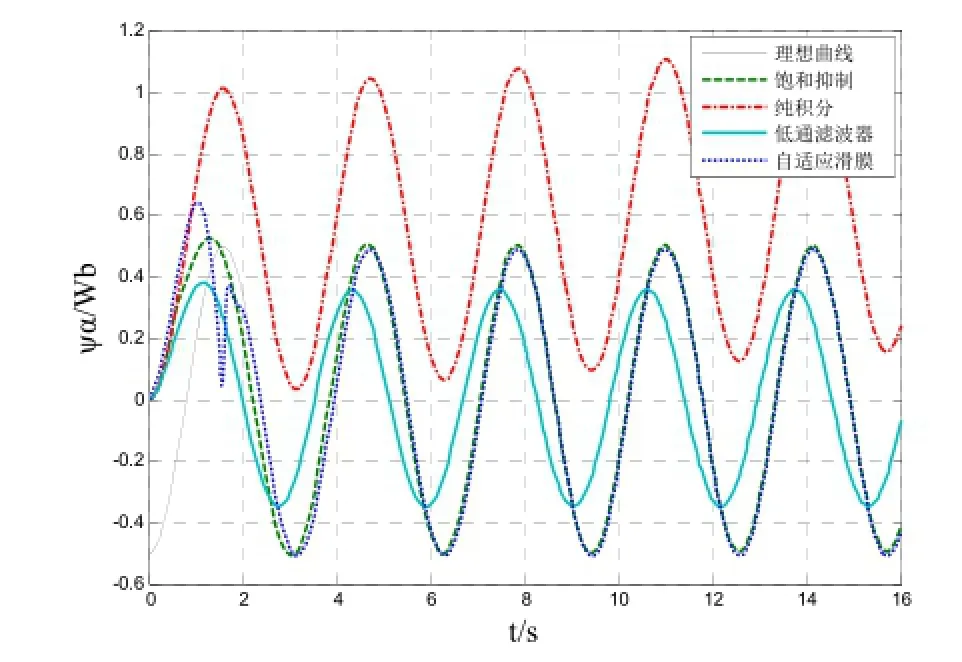
图8 四种方式下稳态波形对比仿真图Fig.8 Simulation diagram of the steady-state waveform comparison

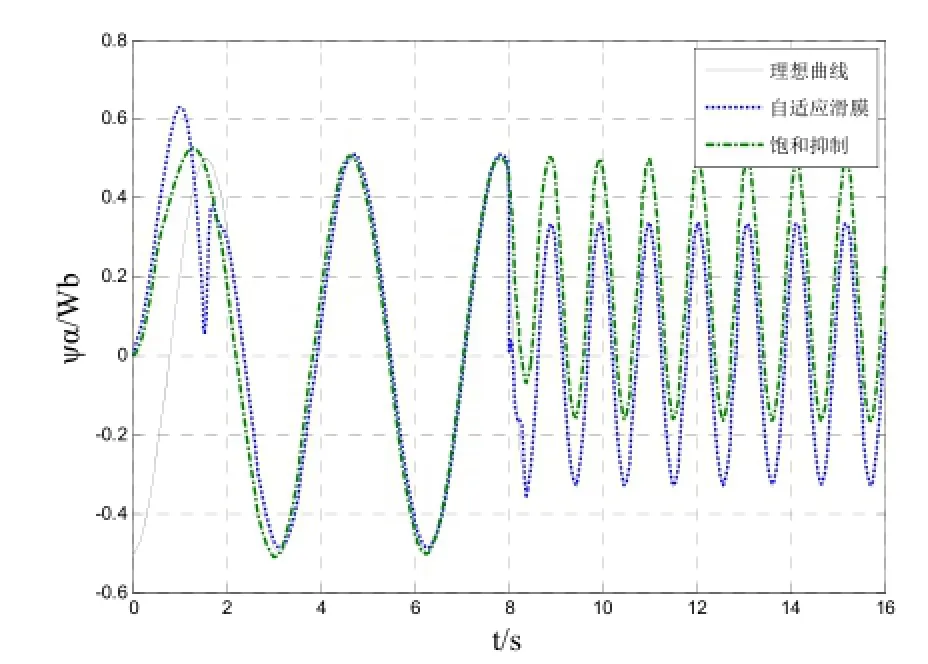
图9 饱和抑制与自适应滑模动态仿真图IFig.9 Simulation diagram of the dynamic waveform comparison between saturation-limited and ASMO

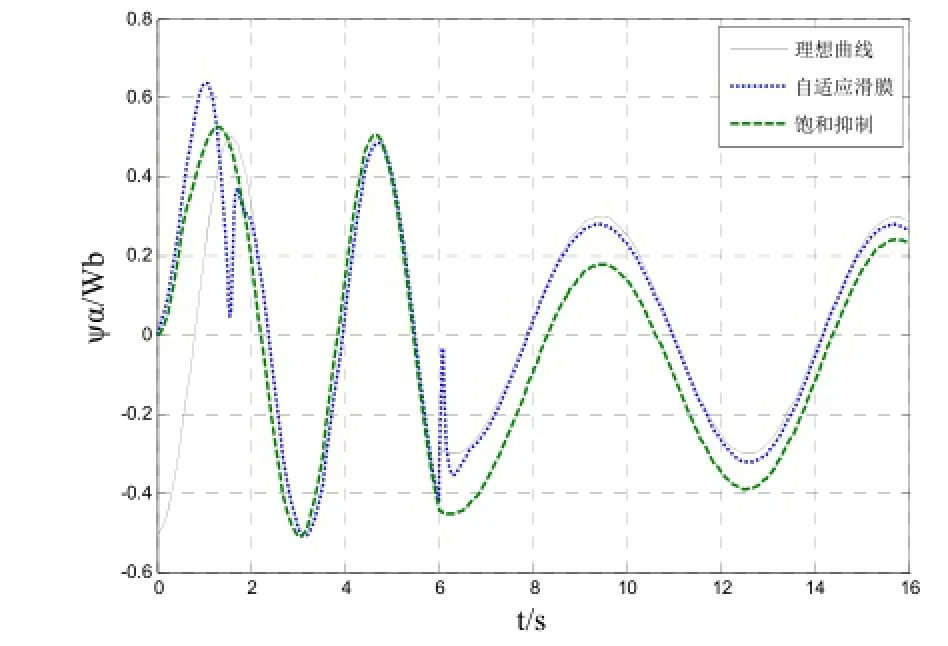
图10 饱和抑制与自适应滑模动态仿真图IIFig.10 Simulation diagram of the dynamic waveform comparison between saturation-limited and ASMO

4.2系统仿真

在Matlab/Simulink中建立仿真模型，仿真参数如下:三相对称电网电源相电压220V/50HZ，交流侧输入电感2.5mH，交流电阻0.28Ω，直流侧滤波电容4 000μF，阻性负载为100Ω，开关频率5KHz，给定直流母线电压650V，χ取0.1，k取490，传统无电压传感控制下和自适应滑模控制下运行于额定工作点的稳态仿真波形如图11和12所示。

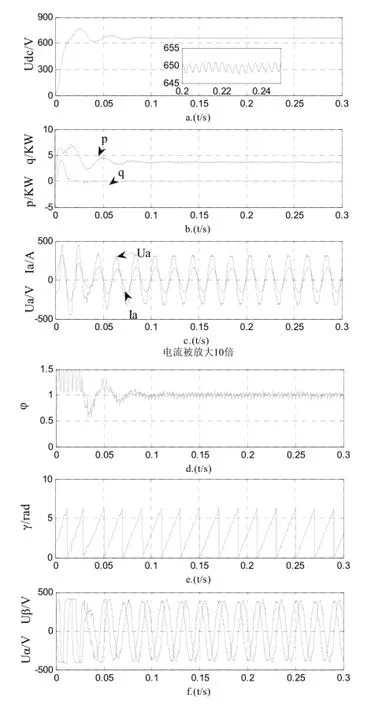
图11 传统无电压传感控制下稳态仿真波形图Fig.11 Traditional VF-DPC under the steady state simulation waveform

图11.a、图11.b和图11.c分别为稳态时的母线电压曲线图、有功功率和无功功率图，以及A相电流和电压图，图11.d、图11.e和图11.f分别为稳态时的虚拟磁链估计值、位置角以及两相静止αβ坐标系电网电压曲线。从图中可以看出，估计的电网电压曲线在一定范围内存在抖动，而且受谐波影响严重，从而导致估计的磁链值精确度下降，母线电压在4V内抖动厉害，相电压和相电流间存在一定的相位差，系统未在单位功率因数下运行。图12为自适应滑模控制下的稳态图，各图分别与图11中相对应，从估计出来的电网电压值可以看出抖动基本消除，而且抑制了谐波的影响，母线电压波动稳定在1V左右，相电压电流同相位。

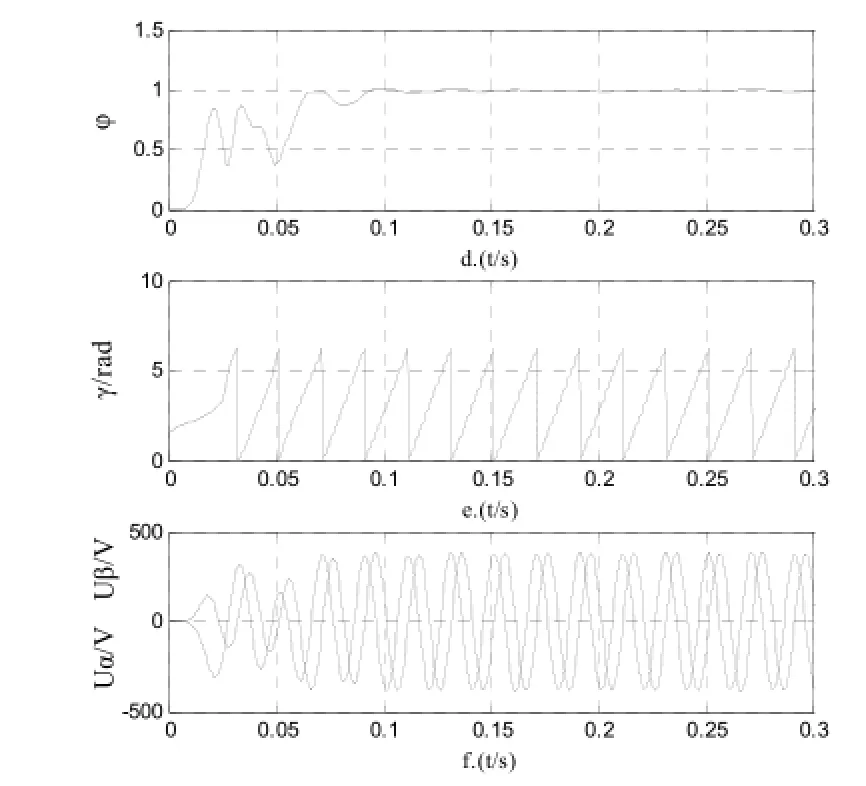
图12 自适应滑模观测器下稳态仿真波形图Fig.12 Adaptive SMO under the steady state simulation waveform

图13 、图14和图15分别为负载突变下两种方法下相电流对比图、母线电压波动对比图及谐波分析，在0.7s将负载增加到50Ω，图13.a为传统无电压传感控制，突变后母线电压急剧下滑，上下波动在15V左右，50ms后恢复平衡，图13.b为自适应滑模控制，突变后波动控制在上下7V左右，恢复时间为25ms。由图14和图15分析可知传统无电压传感控制下网侧电流总谐波畸变率THD较大，为3.15%，自适应滑模控制下网侧电流总谐波畸变率THD为0.51%。

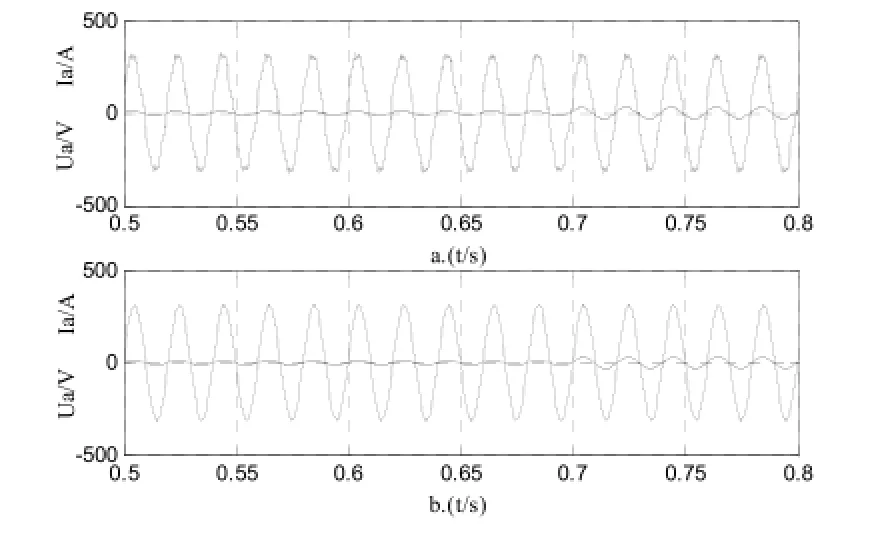
图13 负载阶跃响应时相电压电流波形对比图Fig.13 The A phase voltage and current waveform under the load step

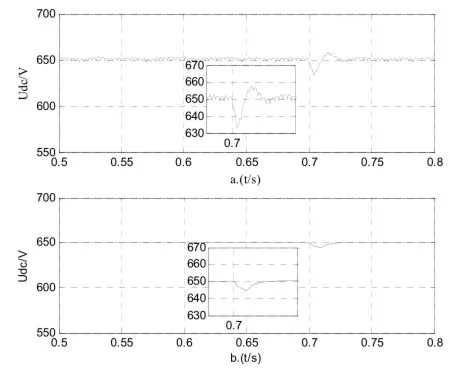
图14 负载阶跃响应时母线电压波形对比图Fig.14 The bus voltage waveform under the load step

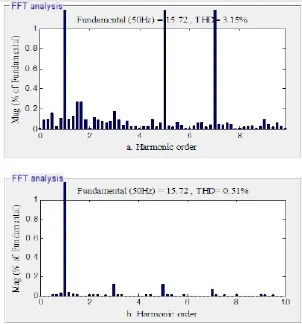
图15 负载阶跃响应时相电流谐波分析对比图Fig.15 Harmonic analysis waveform under the load step

可以得到相比于传统的无电压传感控制，滑膜自适应控制利用s函数对电网电压进行估计避免了网侧电压直接带来的谐波影响，同时引入的自适应控制器除了调整磁链补偿基准外，本身也具备一定的滤波作用，磁链矢量的有效跟踪保证了功率环的快速响应，从而提高了直流侧的动态性能。

为验证在系统参数变化下滑模自适应控制系统的可靠性和有效性，在保证其它参数不变的情况下，分别改变整流器交流侧输入电感L和等效电阻R的值并进行负载突变下的仿真实验，图16a为交流侧等效电阻值摄动（等效电阻值由R逐步摄动到2R）时，整流器直流母线电压波形图；图16b为交流侧输入电感值摄动（输入电感值由L逐步摄动到2L）时，整流器直流母线电压波形图。由图16可知在参数摄动时，直流母线电压均能较快的收敛到给定电压值，说明改进的整流器系统对系统自身参数的摄动具有良好的鲁棒性。

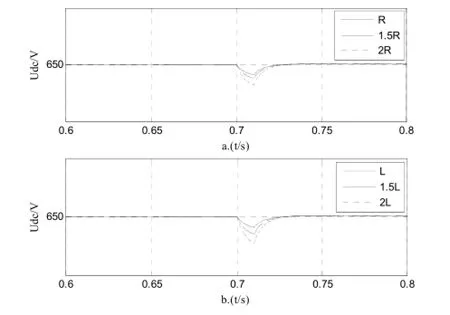
图16 系统参数摄动直流母线电压波形Fig.16 Experimental waveforms when the parameters of DPC system are changed

综上所述，滑模观测器成功引入虚拟磁链观测中，仿真证明了其可行性，所提出的自适应滑模控制策略很好的解决了抖动、谐波处理问题，能够对磁链进行准确的观测，新型的PWM整流器无电压传感控制策略具有更好的动、静态性能。

4.3实验验证

自适应滑模观测器控制策略在自主研发的实验平台进行了实验验证，图17为实验样机控制器、主回路照片。系统主回路采用三电平电压型拓扑结构，输出电压根据实际开关信号来计算，整流器控制采用PWM脉冲整流方式实现四象限整流，采用IGBT元件，控制系统硬件以高速DSP (TMS320F2812)处理器和FPGA为核心器件，基于快速总线技术，可实现高性能矢量控制、模型优化、参数自动辨识等功能[7]，系统主要参数与仿真参数相同。

图17 实验样图Fig.17 The PWM rectifier prototype

图18 为系统在自适应滑模观测器下的稳态实验结果，分别为整流器交流侧的线电压Uab、相电流Ia和母线电压Udc波形图，从图中可以看出，改进的控制系统相电流与相电流同相位，具有单位功率因数特征，母线电压在稳态时波动控制在上下5V范围内。

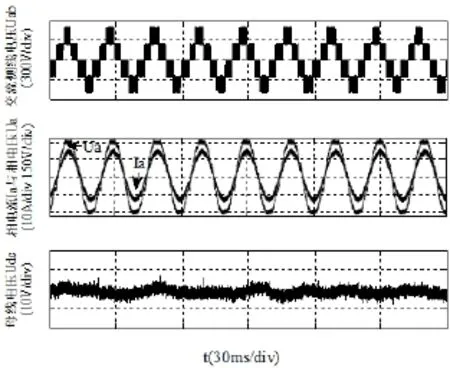
图18 自适应滑模观测器控制下交流侧线电压图、相电压电流波形图、母线电压图Fig.18 The integrated waveform under adaptive SMO in the steady state

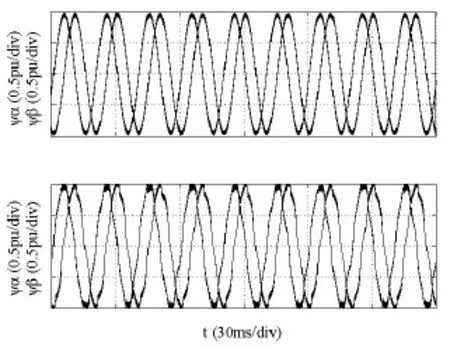
图19 两种观测器下的磁链估计波形图Fig.19 Voltage estimation waveform under two kinds of observer

为了综合比较其控制性能，按照相同的控制参数在平台上分别完成了PWM整流器的传统无电压传感控制和自适应滑模控制，图19为两种控制方式下对两相静止αβ坐标系的磁链估计，可以看到下图的传统控制中估计值存在一定的抖动和干扰，而上图中自适应滑模控制下基本被消除，呈现了比较好的正弦度。图20和图21分别为两种观测器下进行负载突变时的相电流及母线电压波形，对比可以看出自适应滑模观测器下相电流较传统无电压传感下的谐波干扰有所减小，母线电压波动对比可以看出，传统无电压传感下直流母线电压动态响应并不理想，负载突变引起了母线电压的较大波动，波动幅值在30V左右，波动恢复时间较长，而在自适应滑模观测器下母线电压波动幅值减小为14V左右，波动恢复时间较短，系统的动态性能响应得到了明显提高，具有良好的鲁棒性。

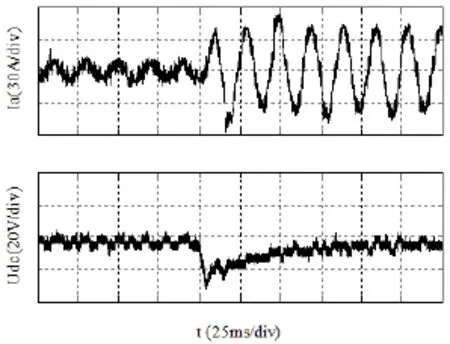
图20 传统无电压传感下负载突变时相电流及母线电压波形图Fig.20 The network A phase current and the bus voltage waveform under traditional VF-DPC in the load step

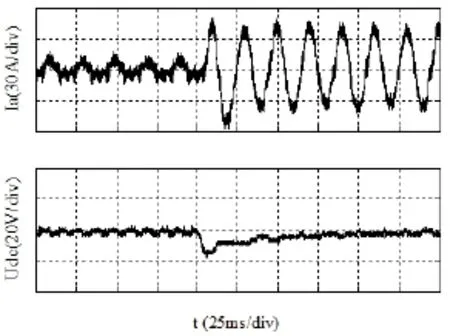
图21 自适应滑模观测器下负载突变时相电流及母线电压波形图Fig.21 The network A phase current and the bus voltage waveform under adaptive SMO in the load step

[1] Z.F. Song, C.L. Xia, T. Liu. Predictive current control of three-phase grid-connected converters with constant switching frequency for wind energy systems[J]. IEEE Transactions on Industrial Electronics, 2013，60 (6)：2451-2464.

[2] 张巍, 尚晓磊, 周元钧, 刘欣博. 一种适用于航空电力作动器负载的三相PWM整流器最大功率控制[J]. 电工技术学报, 2011, 26(8)： 91-98.

Zhang Wei, Shang Xiaolei, Zhou Yuanjun, et al. A maximum power control method of three-phase voltage source rectifiers adapted to aircraft electric actuator load[J]. Transactions of China Electrotechnical Society, 2011, 26(8)： 91-98.

[3] 汪万伟, 尹华杰, 管霖. 双闭环矢量控制的电压型PWM 整流器参数整定[J]. 电工技术学报, 2010, 25(2)： 67-72.

Wang Wanwei, Yin Huangjie, Guan Lin. Parameter setting for double closed-loop vector control of voltage source PWM rectifier[J]. Transactions of China Electrotechnical Society, 2010, 25(2)： 67-72.

[4] P. Antoniewicz, M. P. Kazmierkowski. Virtual flux based predictive direct power control of AC/DC converters with on-line inductance estimation[J]. IEEE Transactions on Industrial Electronics, 2013，55 (12)： 4381-4390.

[5] 姚志垒, 肖岚. 基于改进DPC-SVM的三相并网逆变器[J]. 电力系统保护与控制, 2013, 41(4)： 142-147.

Yao Zhilei, Xiao Lan. Three-phase grid-connected inverters with improved DPC-SVM[J]. Power System Protection and Control, 2013, 41(4)： 142-147.

[6] 张辉, 谭国俊, 钱苗旺. 基于H∞控制与最优跟踪控制相结合的的三相PWM 整流器控制策略[J]. 电工技术学报, 2012, 27(12)： 103-108.

Zhang Hui, Tan Guojun, Qian Miaowang. Study of three-phase PWM rectifier based on a mixture of H∞Control and optimal tracking control[J]. Transactions of China Electrotechnical Society, 2012, 27(12)：103-108.

[7] 邹学渊, 王京, 张勇军. 三电平电压型PWM整流器的SVPWM算法研究[J]. 电气传动, 2010, 40(6)：28-31.

Zou Xueyuan, Wang Jing, Zhang Yongjun. SVPWM Algorithm research of three-level voltage-type PWM [J]. Electric Drive, 2010, 40(6)： 28-31.

[8] Malinowski M, Kazmierkowski M P, Hansen S, et al. Virtual-flux-based direct power control of three-phase PWM rectifiers[J]. IEEE Transactions on Industry Applications, 2001, 37(8)： 1019-1027.

[9] 赵仁德，贺益康．无电网电压传感器三相PWM整流器虚拟电网磁链定向矢量控制研究[J]．中国电机工程学报，2005，25(20):56-61．

Zhao Rende，He Yikang. Virtual line-flux-linkageoriented vector control of three-phase voltage source PWM rectifier without line voltage sensors[J]. Proceedings of the CSEE，2005，25(20):56-61．

[10] 吴凤江, 汪之文, 孙立. PWM 整流器的改进虚拟磁链定向矢量控制[J]. 电机与控制学报, 2008, 12(5)：504-508.

Wu Fengjiang, Wang Zhiwen, Sun Li. Improved virtual flux oriented vector control of PWM rectifier [J]. Electric Machines and Control, 2008, 12(5)：504-508.

[11] 蒋连钿, 张明, 庄革, 等. 三相PWM整流器中基于虚拟无功的锁相环[J]. 电工技术学报, 2013, 28(8)：212-217.

Jiang Liandian, Zhang Ming, Zhuang Ge, et al. A phase-locked loop method for three-phase PWM rectifier based on virtual reactive power[J]. Transactions of China Electrotechnical Society, 2013, 28(8)：212-217.

[12] Dannehl J, Wessels C, Fuchs F W. Limitations of voltage-oriented PI current control of grid-connected PWM rectifiers with LCL filters[J]. IEEE Transactions on Industrial Electronics, 2009, 56(2)： 380-388.

[13] 杨兴武, 姜建国. 电压型 PWM 整流器预测直接功率控制[J]. 中国电机工程学报, 2011, 31(3)： 34-39.

Yang Xingwu, Jiang Jianguo. Predictive direct power control for three-phase voltage source PWM rectifiers [J]. Proceedings of the CSEE, 2011, 31(3)： 34-39.

[14] 王颖杰，伍小杰，戴鹏，等．采用参数辨识及新型主动阻尼控制的LCL滤波脉宽调制整流器[J]．中国电机工程学报，2012，32(15):31-39．

Wang Yingjie，Wu Xiaojie，Dai Peng，et al．PWM rectifier with LCL filter based on parameter identification and a new active damping control[J]. Proceedings of the CSEE，2012，32(15):31-39．

[15] 赵葵银. PWM整流器的模糊滑模变结构控制[J]. 电工技术学报, 2006, 21(7)： 49-53.

Zhao Kuiyin. PWM Rectifier With Fuzzy Sliding Mode Variable Structure Control[J]. Transactions of China Electrotechnical Society, 2006, 21(7)： 49-53.

[16] 陈瑶, 金新民, 童亦斌. 基于滑模控制的三相电压型PWM整流器系统仿真[J]. 系统仿真学报, 2007, 19(8)： 1849-1852.

Chen Yao, Jin Xinmin, Tong Yibin. Simulation of three-phase voltage source PWM rectifier based on sliding-mode control[J]. Journal of System Simulation, 2007, 19(8)： 1849-1852.

[17] 汪万伟, 尹华杰, 管霖. 三相电压型PWM整流器滑模变结构直接功率控制[J]. 华南理工大学学报, 2009, 37(11)： 84-87.

Wang Wanwei, Yin Huajie, Guan Lin. Sliding-mode variable-structure direct power control of three-phase voltage source PWM rectifier[J]. Journal of South China University of Technology, 2009, 37(11)： 84-87.

[18] 王继东, 苏海滨, 王玲花, 等. 基于虚拟磁链直接功率控制的光伏并网逆变器控制策略研究[J]. 电力系统保护与控制, 2009, 37(11)： 70-74.

Wang Jidong, Shu Haibin, Wang Linghua, et al. Study on grid-connected inverter used in PV generation system based on virtual flux-linkage direct power control[J]. Power System Protection and Control, 2009, 37(11)： 70-74.

[19] Su Chen. Direct Power Control of Active Filter with Averaged Switching Frequency Regulation[J]. IEEE Transaction on Power Electronics, 2008, 23(6)：2729-2737.

PWM Rectifiers Based on Adaptive Sliding-mode Observer with Virtual Flux Orientation under Non-line Voltage Sensors Control

Xiao Xiong Zhang Yongjun Wang Jing Li Huade
（Engineering Research Institute University of Science and Technology Beijing Beijing 100083 China）

In the three-phase VSR control system, in order to solve the errors caused by direct current drift and initial value in flux estimation under the traditional no voltage sensors control, a new adaptive sliding-mode observer with virtual flux orientation under non-line voltage sensors control is presented in direct power control(DPC) system. In the new observer, the power supply voltage value is estimated by the switching function based on Sigmoid function. Meanwhile, we design a novel adaptive controller to adjust the compensated reference flux based on virtual flux linkage to be perpendicular to grid voltage. This adaptive sliding-mode observer has improved the virtual flux estimation precision, according to the justified tendency of reduction of the number of the sensors. As an efficient solution to improve the power quality used in DPC system, the proposed control strategy has effectively inhibited the bus voltage fluctuation and harmonic interference. The good dynamic and static performance is verified by simulation and experiment.

PWM rectifiers, virtual flux, adaptive sliding-mode observer, direct power control (DPC), non-line voltage sensors control

TM346

肖 雄 男，1989年生，博士研究生，研究方向为新型控制系统理论，电力电子技术与智能控制。

国家科技支撑计划项目（2012BAF09B02）。

2014-07-10

张勇军(通信作者) 男，1973年生，博士，副研究员，主要从事新型控制系统理论、交流调速控制理论与电力电子应用等领域的研究工作。