模块化多电平变换器模型及稳态特性研究

彭 浩 邓 焰 王 莹 王 昆 何湘宁 赵荣祥

模块化多电平变换器模型及稳态特性研究

彭 浩 邓 焰 王 莹 王 昆 何湘宁 赵荣祥

（浙江大学电气工程学院 杭州 310074）

模块化多电平变换器（Modular Multilevel Converter，MMC）以其高度模块化、高效率、低失真和高可靠性的特点在中高压大容量应用领域有着广阔的前景。本文以上下桥臂总体电容电压之和、上下桥臂总体电容电压之差、桥臂环流以及输出电流为状态变量建立了MMC的四阶大信号模型，并在大信号模型的基础上研究了MMC的稳态特性，得到了环流、桥臂电流以及上下桥臂平均电容电压的精确解析表达式。研究表明，环流主要含有直流分量和二次谐波分量，上桥臂电容电压与下桥臂电容电压的偶次谐波同相，奇次谐波反相，电容电压直流分量与稳态额定值略有差异。最后搭建了三相48模块的MMC仿真平台及实验样机，仿真波形和实验波形均与理论解析表达式高度吻合，验证了所提四阶模型及稳态解析表达式的准确性。

模块化多电平变换器 四阶模型 稳态特性 环流

1 引言

随着全控型器件的电压和功率等级不断提高，基于电压源换流器的柔性直流输电技术在过去数十年里取得了长足的进步，在新能源发电并网、孤岛及弱电网供电、电网互联等领域获得了广泛的应用[1]。传斯贝尔联络工程（Trans Bay Cable Project）的成功运行使模块化多电平变换器（Modular MultilevelConverter，MMC）获得了空前的关注[2-5]。相比于传统的两电平或者三电平拓扑结构，MMC不仅保留了传统电压源换流器有功无功独立可控的特点，而且采用模块串联的方式避免了开关器件直接串联，分散的悬浮电容可以将器件关断电压限制在电容电压范围内，同时输出电平数可自由扩展，电压电流谐波较小。

目前大多数关于MMC的文献均认为子模块电容足够大，忽略子模块电容的谐波电压，将子模块电容看作独立的的电压源，且该电压源电压等于直流母线电压除以子模块数量。将子模块电容视作电压源，可以实现交流侧和直流侧控制解耦，从而将交流侧模型和直流侧环流模型简化为两个独立的一阶模型[6-8]。这种等效方法适用于分析交流侧基波电压电流或者直流侧直流分量，但是它无法反应桥臂环流与子模块电容电压之间的相互耦合关系。

子模块电容电压及桥臂电流等变量的稳态值关系到开关器件、子模块电容以及桥臂电感等系统参数的选型和设计[9-14]。由于桥臂环流与子模块电容电压之间通过开关函数的相互耦合，直接计算这些变量的稳态值变得十分困难。文献[15-17]在假设子模块电容电压平衡的情况下，通过迭代计算得到桥臂环流和电容电压的稳态值。这些方法虽然考虑了电容参数对于电容谐波电压、桥臂谐波电流的影响，但是均将子模块电容电压的稳态直流分量取为直流母线电压除以子模块数量，而事实上，子模块电容电压的直流分量还与负载电流、桥臂二倍频环流及桥臂电感、子模块电容等参数有关。

本文以上下桥臂总体电容电压之和、上下桥臂总体电容电压之差、桥臂环流以及输出电流为状态变量建立了MMC的四阶大信号模型，该模型从本质上反应了桥臂环流与子模块电容电压之间的相互耦合关系。然后在这个大信号模型的基础上研究了MMC的稳态特性，并得到了环流、桥臂电流以及上下桥臂平均电容电压在稳态下的精确解析表达式。最后搭建了一套三相48模块仿真平台和实验样机，仿真及实验结果与理论计算结果高度吻合，验证了理论表达式的准确性。

2 工作原理

2.1拓扑结构

MMC的拓扑结构如图1所示，三相共有6个桥臂，每相包含上下两个桥臂，每个桥臂由N个相同结构的子模块和一个桥臂电感L串联组成。最常用的子模块为半桥模块，由一对带有死区的互补导通的开关管S1、S2和一个电容C组成。

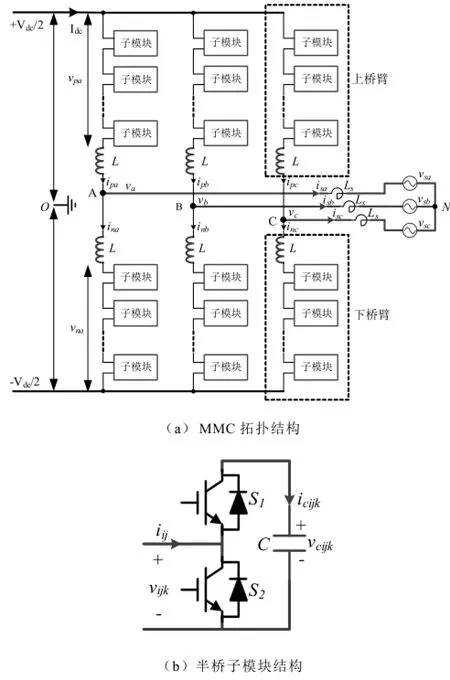
图1 MMC结构图Fig.1 The structure of MMC

当上管S1导通、下管S2关断时，子模块工作于插入模式，子模块端口电压vijk等于电容电压vcijk（i代表上下桥臂编号，i=p,n；j代表相编号，j=a,b,c；k代表子模块编号，k=1,2,···,N）。当上管S1关断、下管S2导通时，子模块工作于旁路模式，子模块端口电压vijk等于0。定义i桥臂j相第k个子模块的开关函数sijk如下:

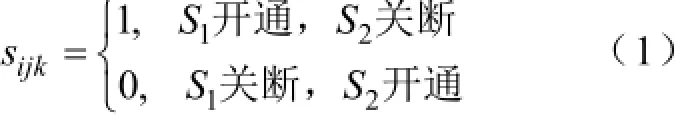
则有

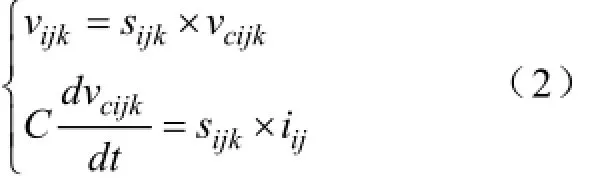
桥臂电压vij为

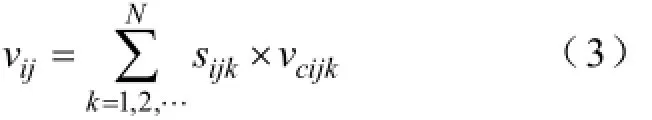
定义桥臂环流icirj为上下桥臂电流ipj、inj之和的一半，结合输出节点的KCL方程可得，

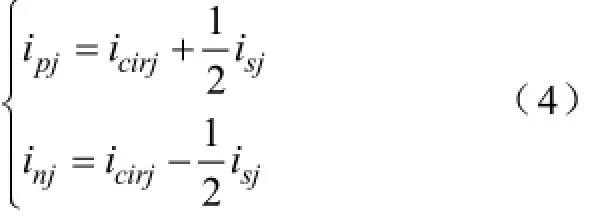
2.2工作原理

将MMC单个桥臂内N个串联的子模块看作一个受控电压源，得到如图2a所示的MMC单相等值电路，上下桥臂均等效为一个受控电压源与一个桥臂电感串联，图中O点为虚拟的零电位点。进一步地，将上下桥臂中的受控电压源分成两个电压源，其中一个受控电压源的电压等于直流输入电压的一半，另一个受控电压源与桥臂电压相关，并将相关的等电位点短路，如图2b所示。由此可以得到图2c所示的简化电路，并做戴维南等效简化之后得到图2d所示的输出等效电路和环流等效电路。

图2 MMC等效电路变换过程Fig.2 The derivation process of equivalent circuit

从图2所示的等效电路可得输出电压的表达式

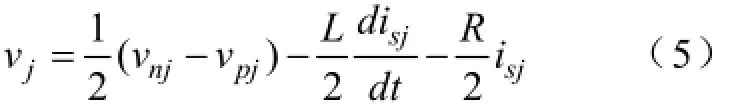
若将图2（d）中输出等效电路中的输出点j前移到jʹ点，可以得到理想的输出电压表达式为

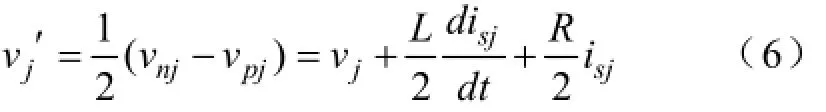
同时从图2（d）可以得到关于输出电流isj和环流icirj的状态方程，

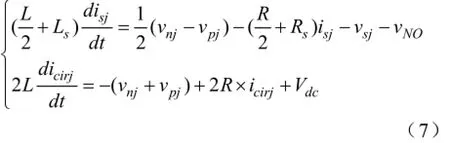
其中R、Rs分别为单个桥臂（包含各子模块和桥臂电感L）和输出电感Ls的等效串联电阻，在三相对称情况下可以认为vNO为零。

由（5）和（6）可知，通过控制上下桥臂的受控电压源，也就是通过控制上下桥臂工作在插入模式的子模块的数量即可以控制输出电流以及桥臂环流的大小。

3 模型及稳态特性分析

3.1四阶大信号模型

在电路建模中，往往将电路中的电感电流、电容电压作为状态变量，但是对于MMC而言，若以电路中的电感电流、电容电压作为状态变量，将会得到一个单相2N+2阶的复杂模型，因此必须适当简化，减少系统中的状态变量。考虑到MMC中同一个桥臂中的电容电压受电容电压平衡算法的作用保持相等，因此同一个桥臂中的N个电容电压可以用一个状态变量来表示，从而将模型降为4阶。

对上下桥臂中的电容电压做一个线性变换，定义上下桥臂总体电容电压之和vcjΣ和上下桥臂总体电容电压之差vcjΔ如下，

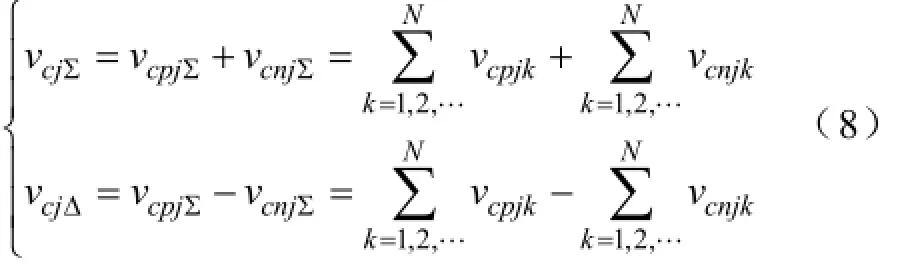
上下桥臂总体电容电压之和vcjΣ反应了整相电容电压平衡情况，上下桥臂总体电容电压之差vcjΔ反应

了上下桥臂总体电容电压之间的均衡情况。定义dj和mj为，

dj反应了上下桥臂投入的子模块的数量之和的平均值，可以控制环流的大小，mj反应了下桥臂与上桥臂投入的子模块数量之差的平均值，可以控制输出电压。

上下桥臂工作在插入模式的子模块个数必定在0到N范围内，因此

（1）系统交流侧理想输出波形为正弦波，不含有谐波，则可以定义j相调制波为mj=mVcos(ωt)/2；

（2）为减少高次谐波环流，一般上下桥臂工作在插入模式的子模块数量之和始终为N，在不加入主动的环流抑制策略时，dj=1/2；

（3）假定系统交流侧电流不含有谐波，交流侧电流只有基波分量，即isj=Ismcos(ωt-θ)，θ为理想输出电压与输出电流之间的相角差；

（4）设桥臂环流的直流分量为Icdc，k次谐波分量的幅值为Ickm，相角为θckω，即

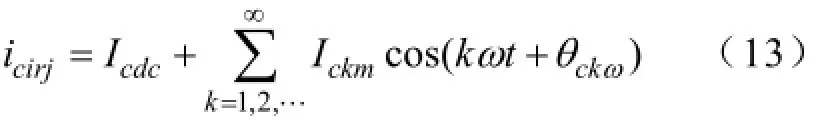
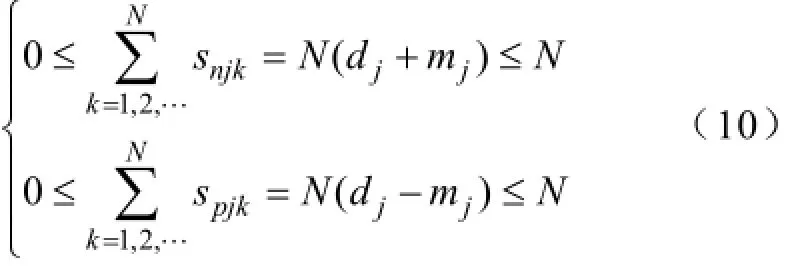
由此可得mj和dj的取值范围，

根据电容的安秒平衡特性及电感的伏秒平衡特性，式（12）中的各个表达式的右边均不含有直流分量，将mj、dj、isj和icirj带入式（12）求取直流分量，可得，

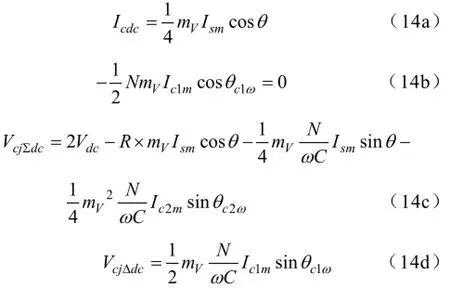
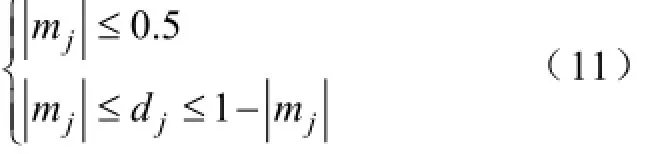
假设上桥臂所有子模块电容电压相等，下桥臂所有子模块电容电压相等。取上下桥臂总体电容电压之和vcjΣ、上下桥臂总体电容电压之差vcjΔ、桥臂环流icirj和输出电流isj作为系统的状态变量，可得到一个四阶大信号模型如下（具体推导过程见附录），

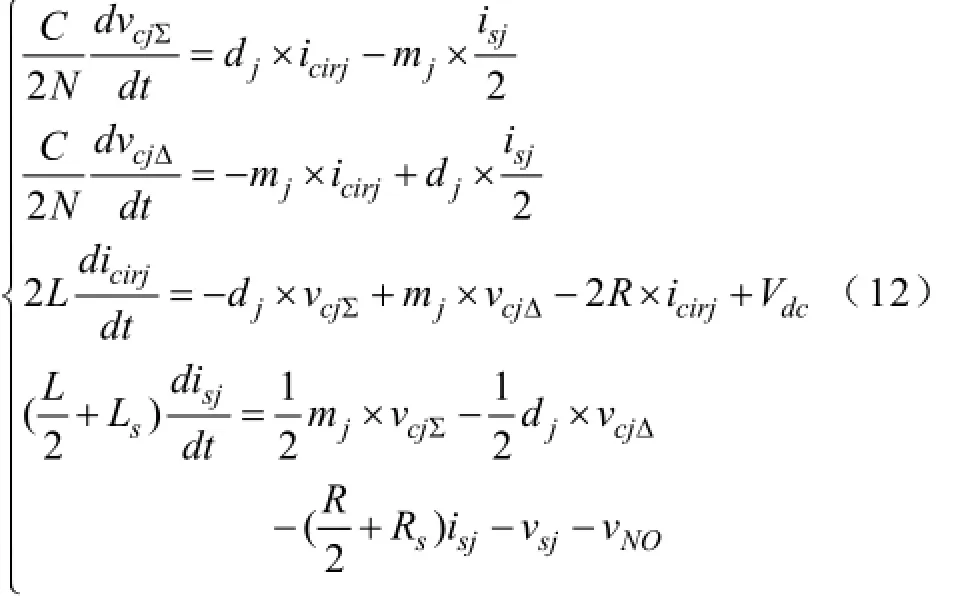
式（12）为一个时变的非线性大信号模型，要得到系统的小信号模型还需要做一定的简化和线性化处理，但是式（12）可以直接用来分析系统的稳态特性。

3.2稳态特性分析

在分析系统的稳态特性前，做如下假定:

其中VcjΣdc、VcjΔdc分别为vcjΣ、vcjΔ的直流分量。

在平衡稳态时，上下桥臂总体电压应维持平衡，则VcjΔdc=0。结合（14b）和（14d），则Ic1m=0，环流中应不含有工频分量。

根据式（12）计算各个变量的交流分量，结合其直流分量，可以得到vcjΣ、vcjΔ的完整的表达式如式（16）和（17）。再将vcjΣ、vcjΔ代入式（12）的第三个表达式，依据式子左右两边各频率分量恒等的关系，可以得到式（18），其中Zkω和φkω分别为桥臂电感L和桥臂等效串联电阻R在k次谐波频率下的阻抗和阻抗角，

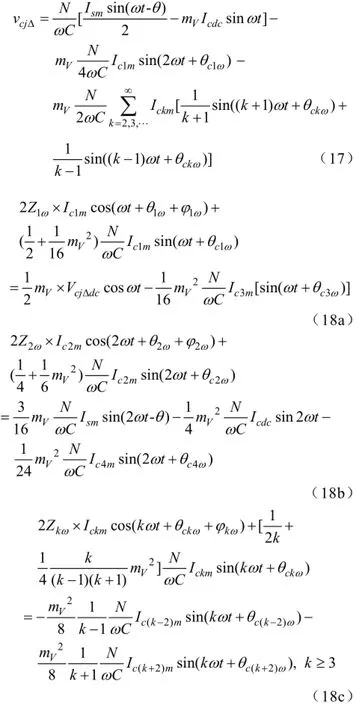
根据（18a），结合Ic1m=0，VcjΔdc=0可知，Ic3m=0。进一步地，结合（18c）的递推表达式，环流中不含有奇次谐波分量，只含有偶次谐波分量，而且随着次数增大迅速衰减，此处主要是根据（18b）求取环流中的二次谐波分量。由于Ic4m很小，（18b）中右边的第三项很小，将其忽略不计，由此可以得到环流中二次谐波分量的解析表达式。

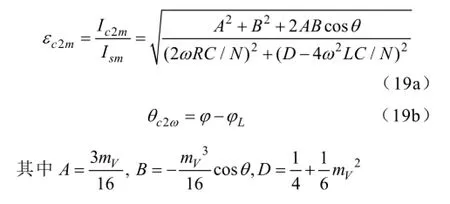
进一步地，可以得到环流icirj、上下桥臂总体电容电压之和vcjΣ和上下桥臂总体电容电压之差vcjΔ的完整表达式，

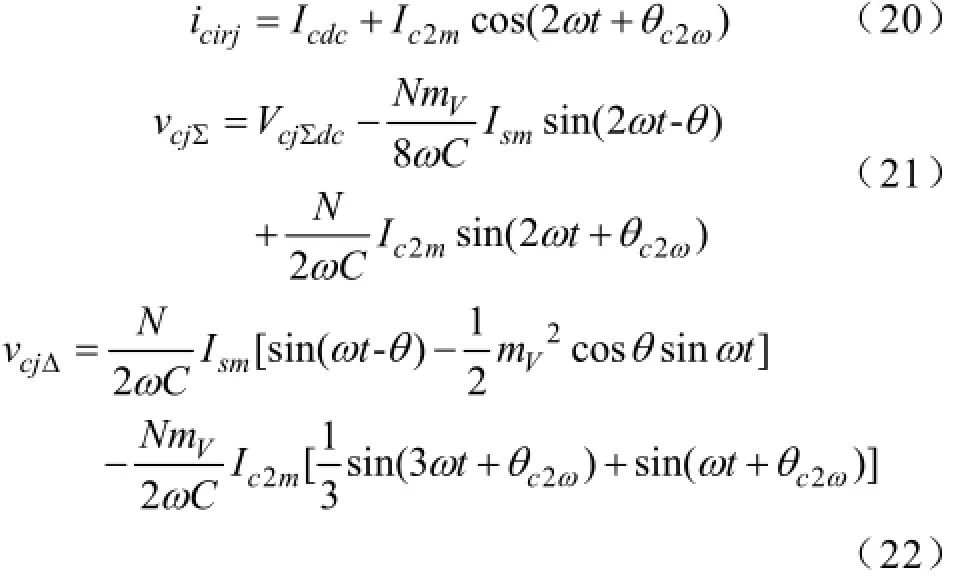
环流icirj主要含有直流分量和偶次（主要是二次）谐波分量，vcjΣ主要含有直流分量和偶次（主要是二次）谐波分量，vcjΔ主要含有工频分量和奇次（主要是三次）谐波分量。

假设上桥臂所有子模块电容电压相等，下桥臂所有子模块电容电压相等，则有，

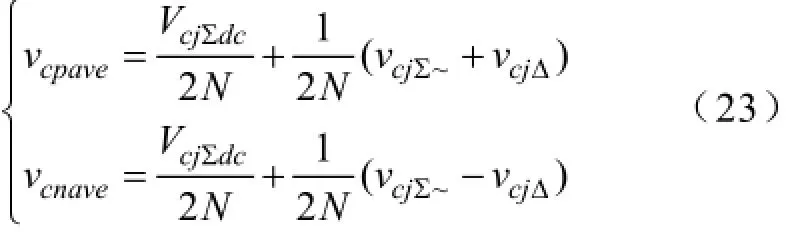
其中vcjΣ～为vcjΣ的交流分量，vcpave、vcnave分别为上下桥臂子模块电容平均电压。上下桥臂子模块电容电压中，偶次谐波幅值相等，相位相同，奇次谐波幅值相等，相位相反。需要说明的是，上下桥臂电容电压中相位相反的工频分量导致电容电压的直流分量与额定值Vdc/N略有差异，这个差值的标幺值为（以Ism/ω/C为标准），

4 仿真及实验验证

为验证本文所提出的大信号模型及其稳态分析的准确性，搭建了一套三相48模块的MMC逆变器仿真平台和实验样机，参数如表1所示，调制方法采用载波移相法，电容电压平衡算法采用工频排序算法。

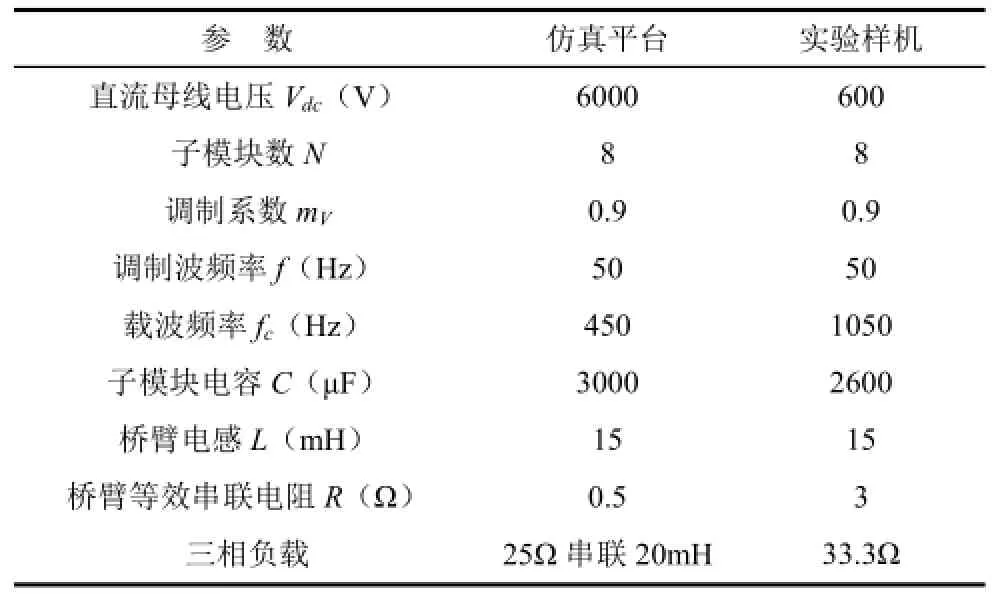
表1 仿真平台及实验样机参数Tab.1 The parameters of the simulation platform and experimental prototype

图3所示为a相各个关键波形的仿真与理论对比图，（a）为输出电压va、电流isa、环流icira以及桥臂电流ipa和ina，（b）为上下桥臂总体电容电压之和vcaΣ、上下桥臂总体电容电压之差vcaΔ及上下桥臂第五个子模块电容电压vcp5和vcn5。需要说明的是，理论计算波形中输出电流幅值和相角由以下公式确定，

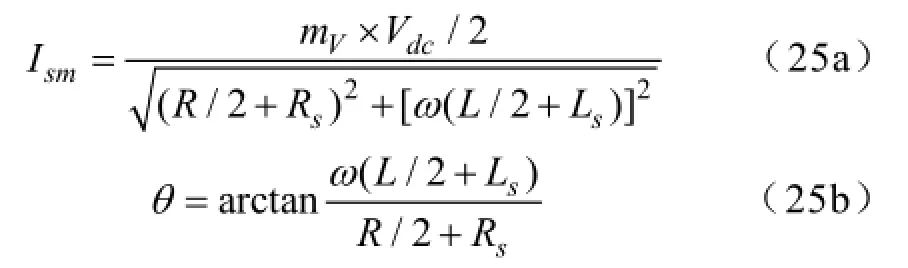
图3 仿真波形与理论波形对比图Fig.3 Comparison between simulation waveforms and theoretical calculated waveforms

将Ism、θ代入式（14）、（20）、（21）和（22）中，得到所有的理论计算波形。除单个电容电压中含有少许的开关次波动外，所有的仿真波形与理论计算波形几乎完全重合，子模块电容电压直流分量为743.12V，与稳态额定值750V略有差异，验证了理论公式的准确性。

图4所示为a相实验波形，输出电压电流畸变较小，电容电压平衡效果较好。图5展示了将实验所得数据导入Matlab与理论计算波形的对比效果，理论计算中输出电流幅值和相角由式（25）确定。通过对比可知，输出电流、桥臂电流与电容电压的实验结果与理论结果完全吻合，桥臂环流的直流分量与二倍频分量幅值基本相等，二倍频分量相角稍有差异，这主要是因为二倍频分量的相角对子模块电容C、桥臂电感L及桥臂等效串联电阻参数非常敏感。本文使用手持式电感表MT4080A测量C和L，但是很难精确测量桥臂等效串联电阻R，估计单个子模块的等效串联电阻为0.25Ω，桥臂电感及回路的等效串联电阻为1Ω，因此取桥臂等效串联电阻R为3Ω。子模块电容电压直流分量为73.66V，比额定值75V略小。对比结果验证了本文所推导的理论公式的准确性。

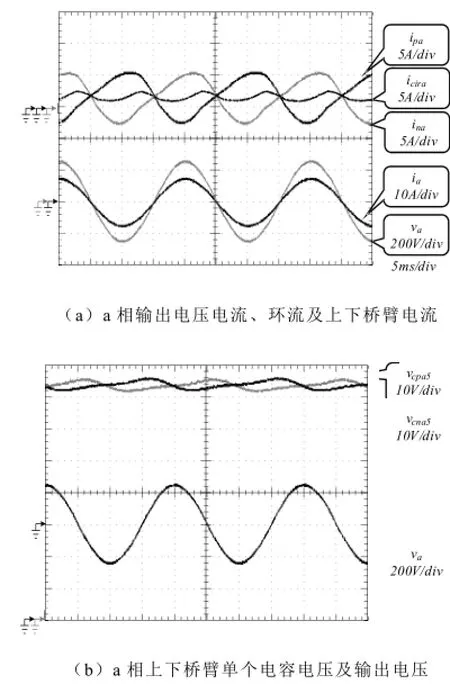
图4 实验关键波形Fig.4 Key experimental waveforms

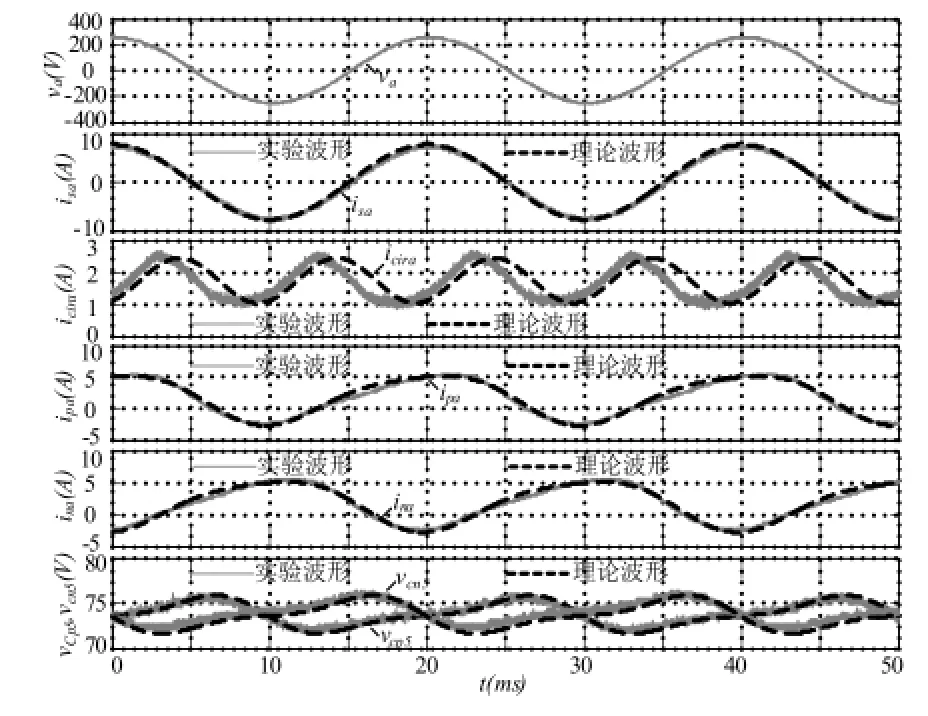
图5 实验波形与理论波形对比图Fig.5 Comparison between experimental waveforms and theoretical calculated waveforms

5 结论

本文以上下桥臂总体电容电压之和、上下桥臂总体电容电压之差、桥臂环流以及输出电流为状态变量建立了MMC的四阶大信号模型，并在大信号模型的基础上研究了MMC的稳态特性，得到了环流、桥臂电流以及上下桥臂平均电容电压的精确解析表达式，指出了子模块电容电压直流分量与其稳态额定值之间的差异，最后通过仿真和实验验证了所建立的四阶模型及稳态解析表达式的准确性。

假设上桥臂所有子模块电容电压相等，下桥臂所有子模块电容电压相等，则

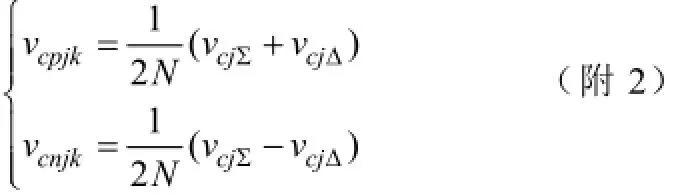
将（附2）代入（附1）结合式（9），即可得到式（12）的四阶模型。

[1] Flourentzou N, Agelidis V G, Demetriades G D. VSC-Based HVDC Power Transmission Systems： An Overview[J]. IEEE Transactions on Power Electronics, 2009, 24(3)： 592-602.

[2] Friedrich K. Modern HVDC PLUS application of VSC in Modular Multilevel Converter topology[C]. 2010 IEEE International Symposium on Industrial Electronics (ISIE), Bari, 2010： 3807-3810.

[3] 雷鸣, 李耀华, 葛琼璇等. 一种新型单桥臂电感模块化多电平变流器及其控制方法[J]. 电工技术学报, 2014, 29(2)： 231-238.

Lei Ming, Li Yaohua, Ge Qiongxuan, et al. A New Modular Multilevel Converter with Single Arm Inductor and Its Control Strategies[J]. Transactions of China Electrotechnical Society, 2014, 29(2)： 231-238.

[4] 武健, 刘瑜超, 徐殿国. 基于模块多电平变换器的并联有源滤波器控制策略研究[J]. 电工技术学报, 2013, (12)： 52-59.

Wu Jian, Liu Yuchao, Xu Dianguo. Control Strategy of Shunt Active Power Filter Based on Modular Multilevel Converter[J]. Transactions of China Electrotechnical Society, 2013, (12)： 52-59.

[5] 杨晓峰, 范文宝, 王晓鹏等. 基于模块组合多电平变换器的STATCOM及其控制[J]. 电工技术学报, 2011, 26(8)： 7-13.

Yang Xiaofeng, Fan Wenbao, Wang Xiaopeng, et al. Static synchronous compensator based on modular multilevel converter based STATCOM and Its control[J]. Transactions of China Electrotechnical Society, 2011, 26(8)： 7-13.

[6] 管敏渊, 徐政. 模块化多电平换流器型直流输电的建模与控制[J]. 电力系统自动化, 2010, (19)： 64-68.

Guan Minyuan, Xu Zheng. Modeling and control of modular multilevel converter in HVDC transmission [J]. Automation of Electric Power Systems, 2010, (19)： 64-68.

[7] 管敏渊, 徐政. 向无源网络供电的MMC型直流输电系统建模与控制[J]. 电工技术学报, 2013, (02)：255-263.

Guan Minyuan, Xu Zheng. Modeling and control ofmodular multilevel converter based VSC-HVDC system connected to passive networks[J]. Transactions of China Electrotechnical Society, 2013, (02)： 255- 263.

[8] Guan M Y, Xu Z. Modeling and Control of a Modular Multilevel Converter-Based HVDC System Under Unbalanced Grid Conditions[J]. IEEE Transactions on Power Electronics, 2012, 27(12)： 4858-4867.

[9] 王奎, 郑泽东, 李永东. 新型模块化多电平变换器电容电压波动规律及抑制方法[J]. 电工技术学报, 2011, 26(5)： 8-14.

Wang Kui, Zheng Zedong, Li Yongdong. Voltage Ripple Principle and Restrain Method of Floating Capacitors in a New Modular Multilevel Converter[J]. Transactions of China Electrotechnical Society, 2011, 26(5)： 8-14.

[10] Yalong L, Wang F. Arm inductance selection principle for modular multilevel converters with circulating current suppressing control[C]. Applied Power Electronics Conference and Exposition (APEC), 2013：1321-1325.

[11] 王姗姗, 周孝信, 汤广福等. 模块化多电平HVDC输电系统子模块电容值的选取和计算[J]. 电网技术, 2011, (01)： 26-32.

Wang Shanshan, Zhou Xiaoxin, Tang Guangfu, et al. Selection and calculation for sub-module capacitance in modular multi-level converter HVDC power transmission system[J]. Power System Technology, 2011, (01)： 26-32.

[12] Wang K, Li Y, Zheng Z, et al. Voltage balancing and fluctuation-suppression methods of floating capacitors in a new modular multilevel converter[J]. IEEE Transactions on Industrial Electronics, 2013, 60(5)： 1943-1954.

[13] Vasiladiotis M, Cherix N, Rufer A. Accurate capacitor voltage ripple estimation and current control considerations for grid-connected modular multilevel converters[J]. IEEE Transactions on Power Electronics, 2014, 29(9)： 4568-4579.

[14] Zhang Y S, Adam G P, Lim T C, et al. Mathematical analysis and experiment validation of modular multilevel converters[J]. Journal of Power Electronics, 2012, 12(1)： 33-39.

[15] 周月宾, 江道灼, 郭捷等. 模块化多电平换流器子模块电容电压波动与内部环流分析[J]. 中国电机工程学报, 2012, (24)： 8-14.

Zhou Yuebin, Jiang Daozhuo, Guo Jie, et al. Analysis of sub-module capacitor voltage ripples and circulating currents in modular multilevel converters[J]. Proceedings of the CSEE, 2012, (24)： 8-14.

[16] Song Q, Liu W, Li X, et al. A Steady-State Analysis Method for a Modular Multilevel Converter[J]. IEEE Transactions on Power Electronics, 2013, 28(8)：3702-3713.

[17] Ilves K, Antonopoulos A, Norrga S, et al. Steady-State Analysis of Interaction Between Harmonic Components of Arm and Line Quantities of Modular Multilevel Converters[J]. IEEE Transactions on Power Electronics, 2012, 27(1)： 57-68.

Research about the Model and Steady-state Performance for Modular Multilevel Converter

Peng Hao Deng Yan Wang Ying Wang Kun He Xiangning Zhao Rongxiang
（College of Electrical Engineering, Zhejiang University Hangzhou 310027 China）

Modular multilevel converter(MMC) is a potential topology for the medium or high voltage and high power applications due to the modular structure, high efficiency, low distortion and high reliability. In this paper, a four order large signal model is built with the state variables of the summation of all the capacitor voltages, the difference between the total voltages of the upper arm and lower arm, the circulating current and the output current. Based on the model, the steady-state performance can be evaluated and the accurate steady-state expressions of the circulating current, the arm current and the average capacitor voltage can be obtained. It can be inferred that the circulating current is mainly composed of the DC component and the second harmonic. For the upper capacitor voltages and the lower capacitor voltages, the even harmonics are with the same phase and the odd harmonics are with the inverse phase. Furthermore, the DC bias of the capacitor voltage is a little different from the rated value. At last, a three-phase 48 sub-modules platform is built to verify the accuracy of the four order model and the steady-state expressions. The simulation and experimental results are highly matched with the theoretical expressions.

Modular multilevel converter (MMC), four order model, steady-state performance, circulating current

TM464

彭 浩 男，1989年生，博士研究生，研究方向为模块化多电平变换器。

2014-- 改稿日期 2014--

邓 焰 男，1973年生，副教授，硕士生导师，研究方向为微电网系统控制及建模、模块化多电平变换器等。