基于Adaline神经网络参数辨识的含DG配电网的电压稳定性分析

杨志淳

（国网湖北省电力公司电力科学研究院，武汉 430077）

随着分布式电源（DG）在配电网渗透率的增大，其对配电网电压稳定性的影响将不容忽视。传统电力系统电压稳定性分析一般是基于连续潮流法、潮流多解法、非线性规划法及特征结构法等。连续潮流法在考虑非线性因素的同时，有较强的算法适应性，但要计算负荷不断增长下的潮流状态，计算量较大；潮流多解法利用潮流方程的高、低电压解求取临界点；非线性规划法利用Kuhn-Tucher条件处理临界点约束求解问题，但不易进行有功和无功解耦处理；零特征根法根据潮流方程在临界点处雅克比矩阵奇异的性质，用牛顿法解算，在理论上可以直接求出临界点，但方程的阶数比普通潮流方程高许多，计算量较大。

近年来随着实时测量技术的发展，戴维南等值方法应用而生，该方法可有效化简网络，快速分析系统的电压稳定性。文献［1］基于阻抗动态步进的PVZ曲线快速求解方法，利用改进的节点附加注入法快速求解某一状态下的戴维南等值参数，从而求得电压稳定临界点。文献［2］采用递推最小二乘法对系统的戴维南等值参数进行辨识，根据已有的电压稳定性指标对系统电压稳定性进行评估。文献［3］基于扩展PV曲线数学表达式的基础上，利用比函数极小化寻优搜索算法来评估电网等值参数。文献［4］考虑戴维南等值参数在跟踪计算过程中不断变化的实际情况，提出了基于全微分的戴维南等值参数跟踪计算方法。文献［5］采用平方根滤波器进行戴维南等值参数估计。

本文利用戴维南等值电路对含DG的配电网进行电压稳定性分析。将含有DG的配电网络等值为3节点系统，在该等值系统的基础上提出了电压稳定性新指标；将Adaline神经网络用于戴维南等值系统的参数辨识中，戴维南等值电势及等值阻抗作为Adaline神经网络的权值，通过测量单元采集到的电压和电流相量对系统进行训练，得到戴维南等值系统的电势及阻抗。以此为基础，对分布式电源接入对配电网的电压稳定性进行了评估。

1 含DG的配电网电压稳定性指标

对某一含有DG的节点，仅保留该DG及其负荷，将系统其余部分用电压源和阻抗等效，图1为等效后的3节点系统配电网络［6］。

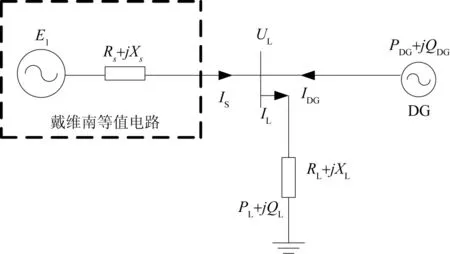
图1 含DG配电网的戴维南等效电路

图中戴维南等值电势幅值为E1，设其相角为0°；戴维南等值阻抗为Zs＝Rs＋j Xs；负荷节点电压幅值为UL，相角为θ；设负荷有功和无功功率分别为PL和QL，分布式电源的有功和无功功率分别为PDG和QDG。

1.1 电压稳定性指标

图1中负荷节点的视在功率为：

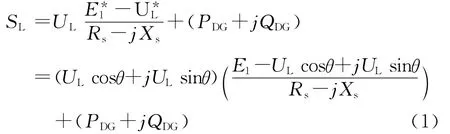
可得负荷有功功率及无功功率为：

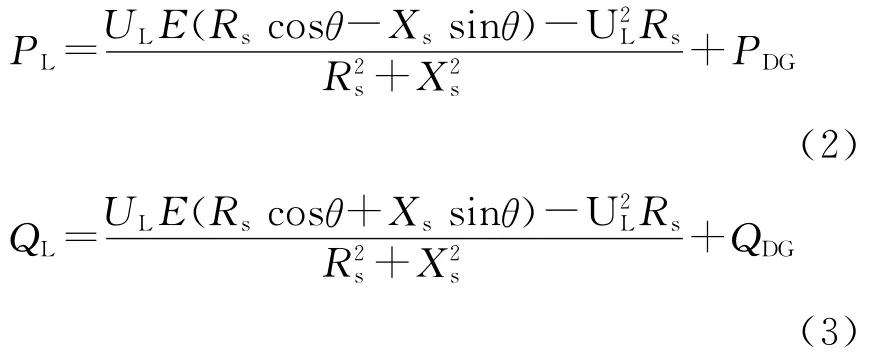
通过移项得到：

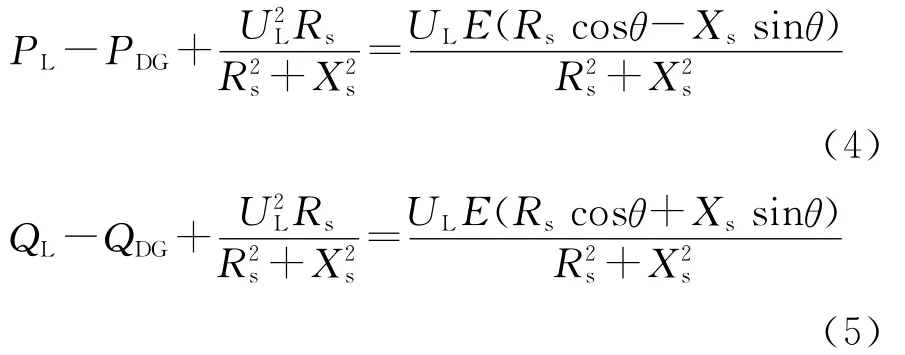
在式（4）和式（5）中消去θ，得到：

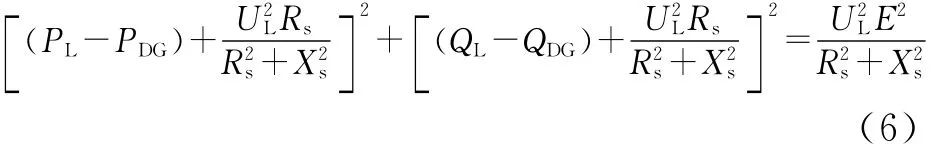
对式（6）进行简化可得到：

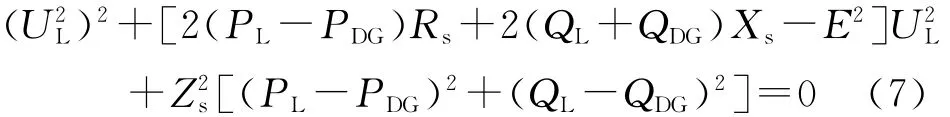
求解式（7）所示的一元二次方程得到：

在临界稳定时，电压仅存在一个解，则：

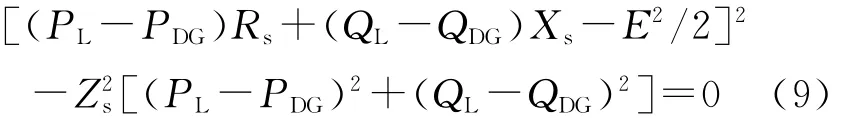
该唯一解为：

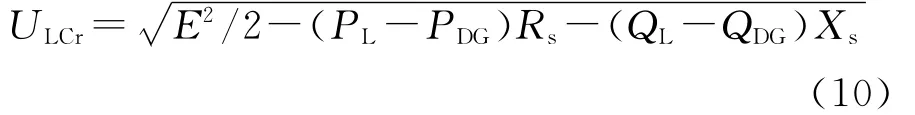
据此可定义电压稳定性指标为：

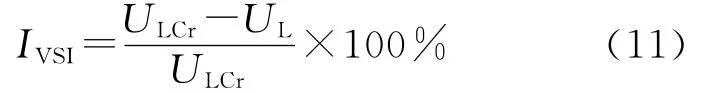
式中 ISVI——时间断面t时节点电压稳定裕度指标；ULCr——临界电压值。

当ISVI≥1时，说明所观测节点电压不稳定，如果ISVI＜1时，说明所观测节点电压稳定，ISVI＝1为电压水平达到稳定极限。

1.2 负荷节点的等效阻抗与该节点戴维南等值阻抗的关系

在不含DG的系统中，负荷节点的等效阻抗等于该节点网络的戴维南等值阻抗时，为电压稳定的临界点。该结论作为电压稳定判据已经被普遍认同［7］。但如果所观测节点含DG时，这种判据是否成立，本节对其进行证明。

根据式（11）的定义：

（1）当所观测节点不包含DG时，即PDG＝0，QDG＝0，由式（10）可知有：

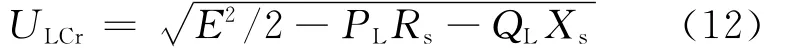
负荷阻抗ZL满足：

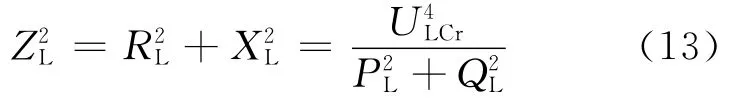
将式（12）代入式（13），可得

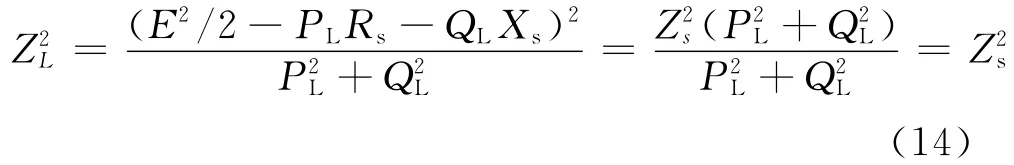
式（14）说明，当所观测节点不包含DG时上述电压稳定性判据成立。

（2）当负荷节点接入DG时，

将式（10）代入式（13），得到：

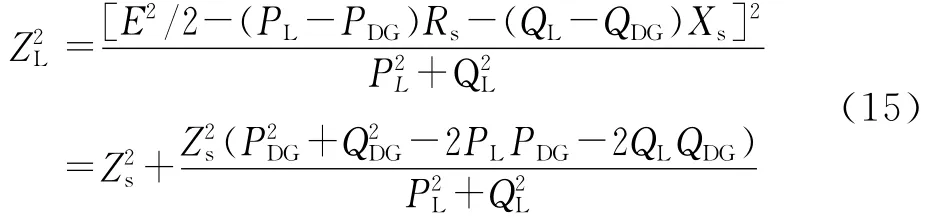
可以看到，当所观测节点含DG时，在达到稳定运行极限，负荷节点的等效阻抗不等于该节点网络的戴维南等值阻抗，说明上述电压稳定性判据在系统含DG时不成立。

2 戴维南等值电路的参数辨识

2.1 系统待辨识参数

式（10）中，负荷有功功率PL和无功功率QL以及DG输出的有功功率PDG和无功功率QDG可通过测量直接得到，故只需求出E、Rs和Xs便可求出电压临界值。由图1可以得出：

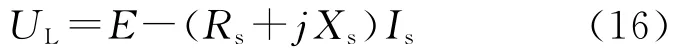
将戴维南等值系统的电势以及负荷节点电压和电流分解为直角坐标型式：

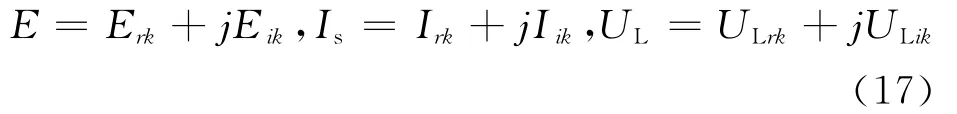
则式（17）可分解为：

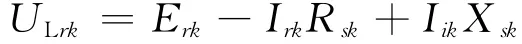
式中下标k代表第k个测量量，以下含义相同。

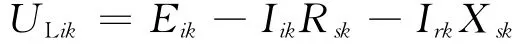
将上面两式相加，得到：

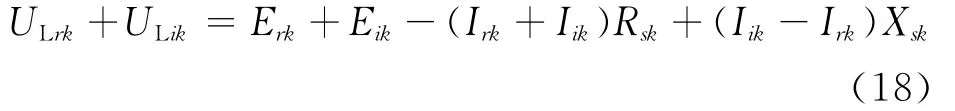
可直接测量得到节点的电压相量及相关联支路的电流相量，即ULrk、ULik、Irk、Iik为已知量，而Erk、Eik、Rsk、Xsk为待辨识参数。

2.2 Adaline神经网络

图2所示为自适应线性神经网络（Adaline）的基本结构，它是一个由输入层和输出层构成的单层前馈型网络［8－11］。

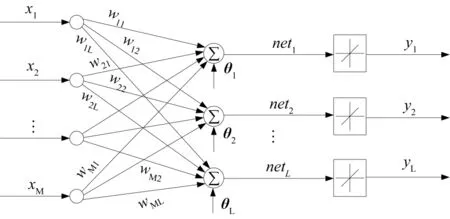
图2 Adaline神经网络基本结构

对于具有M个输入和L个输出的线性神经网络，其输出层的第i个神经元的输入总和及输出分别为：

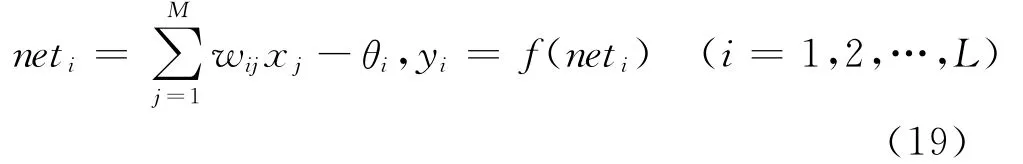
式中 θi——输出层神经元i的阈值；M——输入层节点数；L——网络输出节点数；f（·）——激活函数，一般线性神经网络选择f（x）＝x，因此对每一样本Xp有：

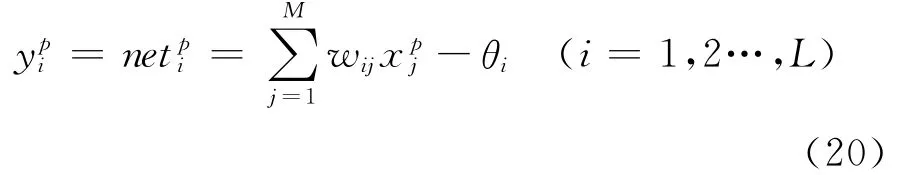
若对于每一样本的二次型误差为：

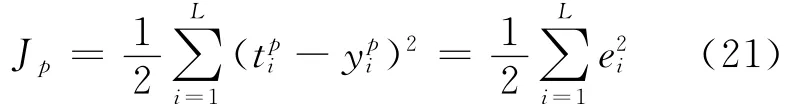
则系统对所有N个训练样本的总误差为：

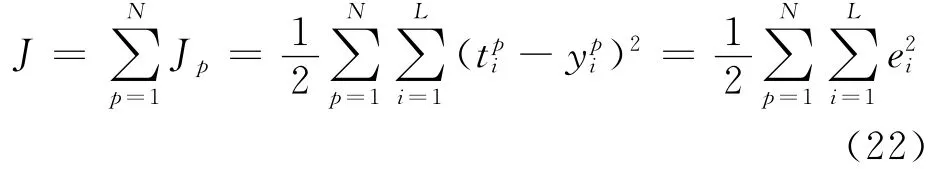
Adaline神经网络的加权系数修正采用Widrow-Hoff学习规则，又称为最小均方差误差算法（LMS）。它的实质是利用梯度最速下降法，使权值沿误差函数的负梯度方向改变。Widrow-Hoff学习规则的权值变化量正比于网络的输出误差及网络的输入矢量。根据梯度法，可得输出层任意神经元i的加权系数修正公式为：

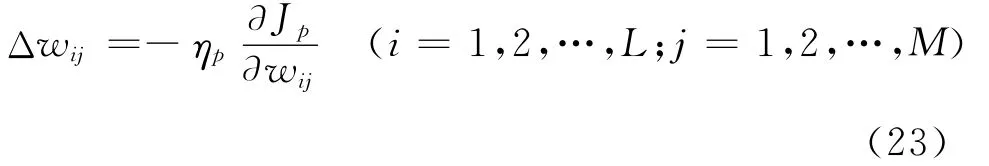
式中 ηp——学习效率；α为常数；当0﹤α﹤2时，可使算法收敛。

ηp＝α／Xp可以看到，ηp将随输入样本Xp的不同而自适应调整。

因为：

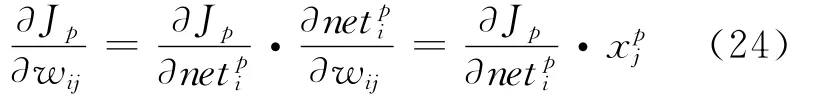
由于有：

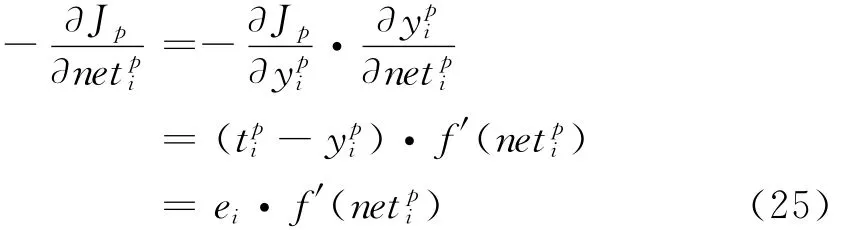
由于激活函数f（·）为线性函数，则：

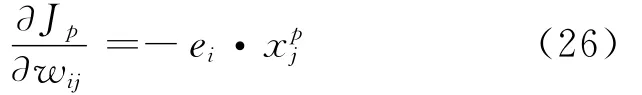
因此输出层任意神经元i的加权系数修正量为：

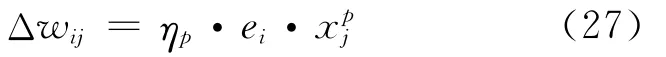
因此任意神经元i的加权系数修正公式为：

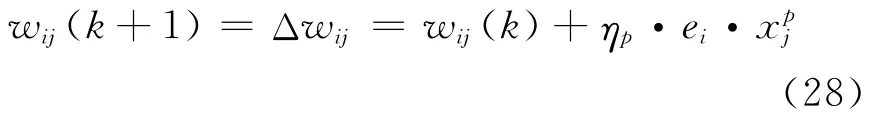
2.3 基于Adaline神经网络的参数辨识

本文应用2.2中Adaline神经网络及加权系数修正方法对式（18）中的未知参数Erk、Eik、Rsk、Xsk进行辨识。如图3所示，所设计的Adaline神经网络包含4个输入：1、1、－Irk－Iik、Iik－Irk和1个输出：Urk＋Uik，权值为Erk、Eik、Rsk、Xs。

采用该神经网络进行参数辨识的步骤如下：

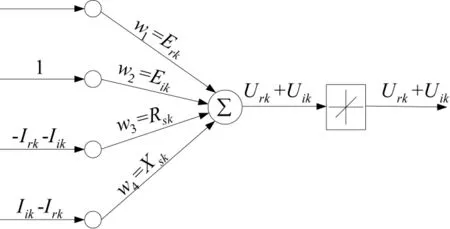
图3 用于参数辨识的Adaline神经网络

（1）初始化；通常随机设置神经元之间的连接权值为较小的非零随机值；

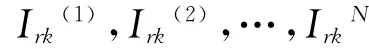
（3）按式（20）计算输出层神经元的输出；

（4）按式（22）计算总误差，当误差小于设定阈值时辨识结束；否则按式（28）调整加权系数wij，并返回步骤（3）；

（5）辨识结束，所得到的加权系数即为需要辨识的系统参数。

3 仿真分析

3.1 仿真模型及其参数

本文以如图4所示的IEEE 33节点配电系统为对象进行算法验证。该系统电压基准值为12.66 k V，视在功率基准值为10 MVA，根节点电压标幺值为1.05，其它详细参数见文献［21］。

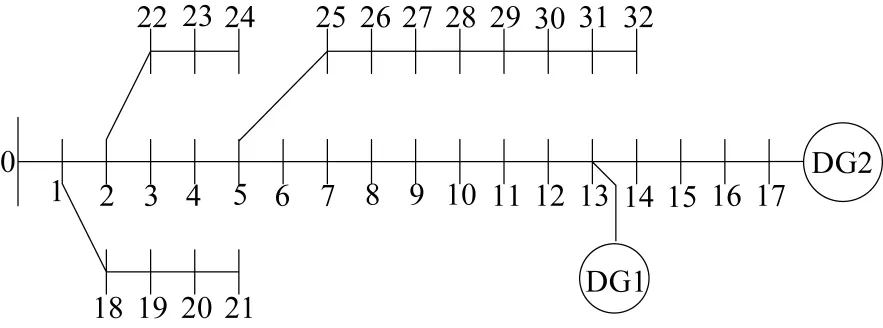
图4 含DG的IEEE 33节点配电网

3.2 未接入DG时的电压稳定性分析

根据式（11）计算得到系统各节点的电压稳定性指标如表1所示。

从表1可以看出，系统各个节点的电压稳定性指标均小于1。以恒定功率因素逐渐增加负荷节点上的功率直到系统临近电压崩溃，我们可以获得每个负荷节点在不同的负荷增长率？时的电势、阻抗以及电压稳定性。

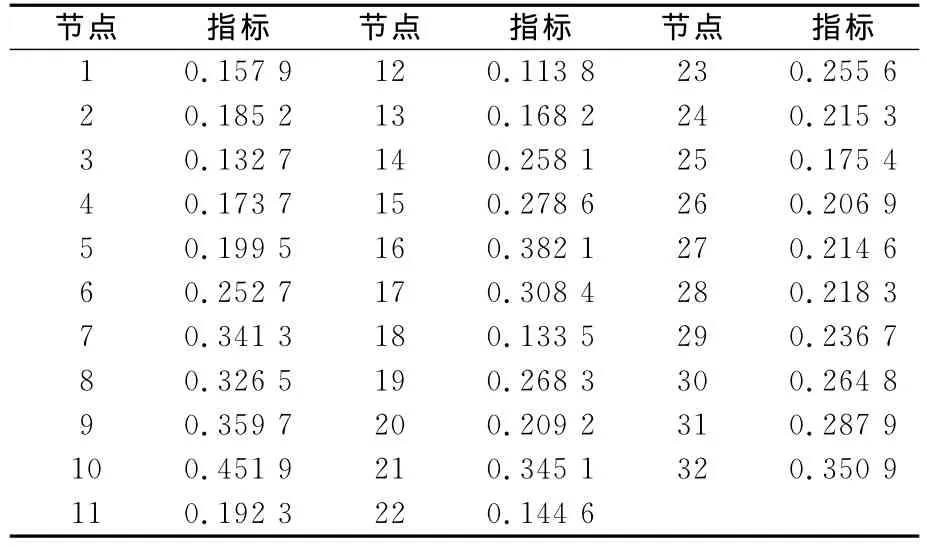
表1 不含DG时的电压稳定性指标

表2和表3给出了当负荷增长率达到3时系统的戴维南等值电路参数与电压稳定性指标。图5给出了负荷增长时的负荷增长率？与电压幅值的变化曲线。

从图5可以看出，随着负荷的增长，节点13、14、15、16、17的电压幅值逐渐减小，在负荷增长率达到3时，节点17的电压幅值超出临界电压水平，从表3可以看出，这些节点的电压稳定性指标有如下关系：ISVI，17＞1＞ISVI，16＞ISVI，15＞ISVI，14＞ISVI，13，这与图5中的结果一致，说明当系统不含DG时，该电压稳定性指标可以很好地反应系统电压稳定状况。

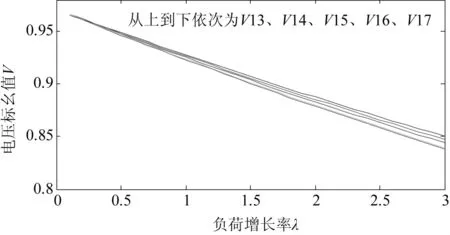
图5 负荷节点的V-λ特性曲线

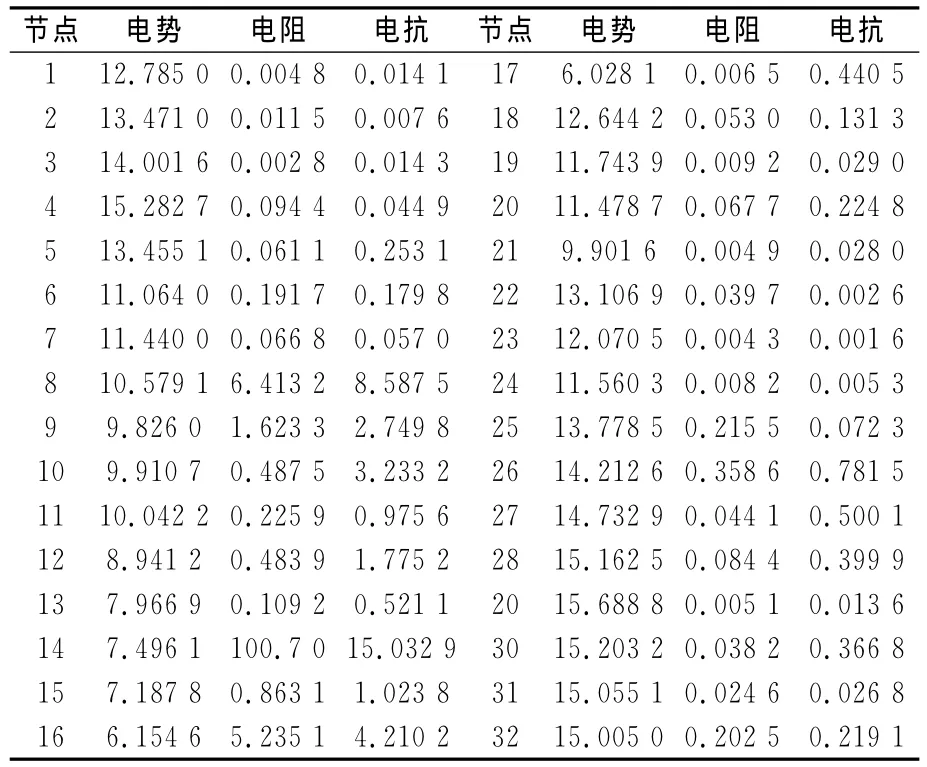
表2 各节点的戴维南等值电势和阻抗

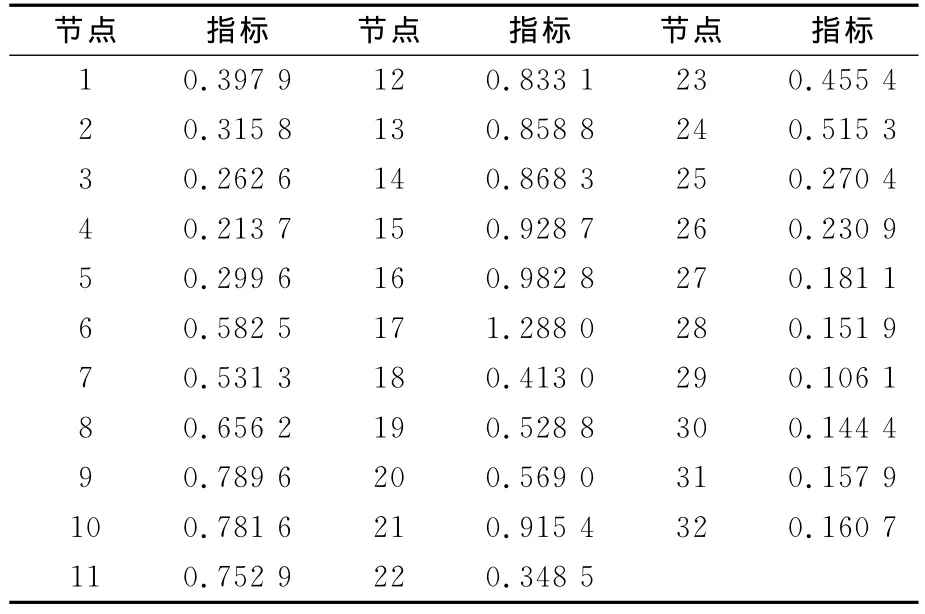
表3 负载增大时的电压稳定性指标

3.3 接入DG后电压稳定性分析

在节点13和节点17接入DG，其容量均为0.8MVA＋j0.8MVar。此时节点13、14、15、16、17的等值参数与电压稳定性指标如表4所示。

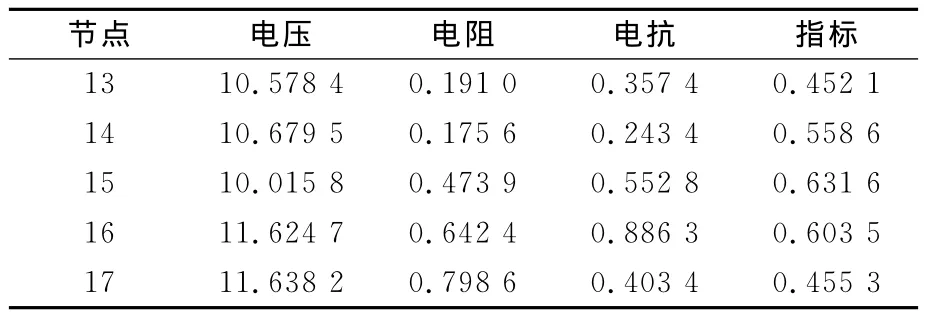
表4 含DG时的电压稳定性指标

从表4可以看出，在接入DG以后，节点13、14、15、16、17的电压稳定性指标重新小于1。此时，再以恒定功率因素逐渐增加负荷节点上的功率直到系统临近电压崩溃，当负荷增长率达到5时，系统再次出现电压稳定性指标大于1的节点，相应的戴维南等值参数与电压稳定性指标如表5所示。图6给出了负荷增长时的负荷增长率λ与电压幅值的变化曲线。

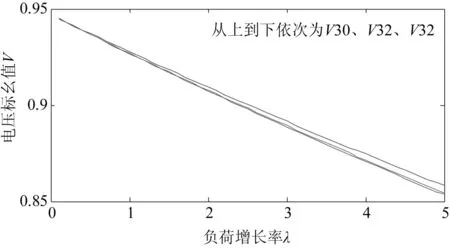
图6 负荷节点的V-λ特性曲线

从图6可以看出，在接入DG后，随着负荷的增长，节点30的电压幅值超出临界电压水平，节点31、32的电压幅值趋于临界电压。从表5可以看出，这些节点的电压稳定性指标均存在如下关系：ISVI，32＞1＞ISVI，31＞ISVI，30，这与图6中的结果一致，说明系统中含DG时，该电压稳定性指标可以很好地反应系统电压稳定状况。

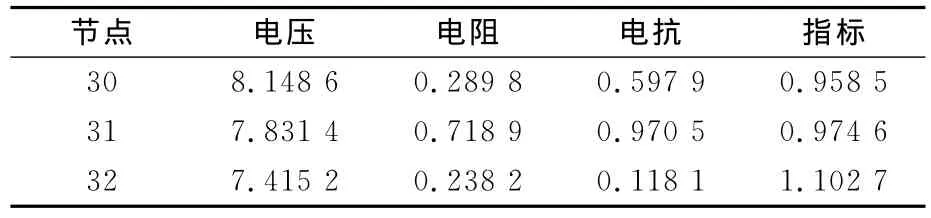
表5 含DG时的电压稳定性指标

4 结论

本文首先根据戴维南等值理论，将含DG的配电网络等值为3节点系统，在此基础上提出了电压静态稳定性新指标；应用了Adaline神经网络对戴维南等值系统的参数进行辨识，以实时连续采集到的电压和电流作为样本，采用最小均方差误差算法神经网络加权系数进行修正，辨识所得的加权系数即为戴维南等值系统的电势及阻抗。在IEEE33节点系统中，对DG接入前后配电网在不同负荷水平下的电压稳定性进行了分析，结果表明不接入DG时，随着负荷的增大，配电网的静态电压稳定性将逐步变差，而DG的接入能在一定程度上提高配电网的静态稳定性。本文所提出的静态电压稳定性指标，基于Adaline神经网络的等值系统辨识方法及以此为基础的DG接入对配电网电压稳定性的影响分析为研究分布式电源接入对配电网的影响提供了较好的理论和方法。

［1］ 刘宝柱，于继来.基于阻抗动态步进的PVZ曲线快速求解［J］.中国电机工程学报，2004，24（9）：104－109.

LIU Bao-zhu，YU Jin-lai.Fast computation of PVZ curves with impedance dynamic step［J］.Proceedings of the CSEE，2004，24（9）：104-109.

［2］ 李大虎，曹一家.基于同步相量测量的实时电压稳定分析方法［J］.电力系统自动化，2006，30（12）：17-22.

LI Da-hu，CAO Yi-jia.Synchronous phasor measurements based real time voltage stability analysis method［J］.Automation of Electric Power System，2006，30（12）：17-22.

［3］ 李娟，刘修宽，曹国臣，等.一种面向节点的电网等值参数跟踪估计方法的研究［J］.中国电机工程学报，2003，23（3）：30-33.

LI Juan，LIU Xiu-kuan，CAO Guo-chen.A tracking estimation method for network equivalent parameters of facing the node［J］.Proceeding of CESS，2003，23（3）：30-33.

［4］ 汤涌，孙华东，易俊，等.基于全微分的戴维南等值参数跟踪算法［J］.中国电机工程学报，2009，29（13）：48-53.

TANG Yong，SUN Hua-dong，YI Jun，et al.Tracing algorithm for thevenin equivalent parameters based on complete differential equation［J］.Proceedings of the CSEE，2009，29（13）：48-53.

［5］ 闫常友，刘建飞，刘奇逊，等.基于平方根滤波的网络等值算法［J］.继电器，2006，，34（3）：41-45.

YOU Chang－you，LIU Jian-fei，LIU Qin-xun，et al.Research on real time equivalent based on square root algorithm［J］.Relay，2006，34（3）：41-45.

［6］ 赵晋泉，杨友栋，高宗和.基于局部相量测量的电压稳定评估方法［J］.电力系统自动化，2010，34（20）：1-6.

ZHAO Jin-quan，YANG You-dong，GAO Zong-he.A review on on-line voltage stability monitoring indices and methods based on local phasor measurement［J］.Automation of Electric Power System，2010，34（20）：1-6.

［7］ 汤涌，林伟芳，孙华东，等.考虑负荷变化特性的电压稳定判据分析［J］.中国电机工程学报，2010，30（16）：12-18.

TANG Yong，LIN Wei-fang，SUN Hua-dong，et al.A-nalysis of voltage stability criterion considering load characteristics［J］.Proceedings of the CSEE，2010，30（16）：12-18.

［8］ 刘侃，张兢.基于自适应线性元件神经网络的表面式永磁同步发电机参数在线辨识［J］.中国电机工程学报，2010，30（30）：68-73.

LIU Kan，ZHANG Jing.Adaline neural network based online parameter estimation for surface mounted permanent magnet synchronous machines［J］.Proceedings of CSEE，2010，30（30）：68-73.

［9］ 李国勇.神经模糊控制理论及应用［M］.北京：电子工业出版社，2009.

［10］ 蔡忠法，陈隆道，陈国志.基于自适应神经网络的谐波分析模型与算法［J］.电工技术学报，2008，23（7）：118-123.

CAI Zhong-fa，CHEN Long-dao，CHEN Guo-zhi.Harmonic analysis model and algorithm based on adaptive neural network［J］.Transactions of China Electrotechnical society，2008，23（7）：118-123.

［11］ 祝燕萍，方鸽飞.基于动态自适应神经网络和人体舒适度的短期负荷预测［J］.电力系统保护与控制，2012，40（1）：56-61.

ZHU Yan-ping，FANG Ge-fei.Short-term load forecasting based on dynamic adaptive artificial neural network and human body amenity indicator［J］.Power System Protection and Control，2012，40（1）：56-61.

［12］Distribution system analysis subcommittee report.Radial distribution test feeders［C］.Power engineering society winter meeting，2001：908-912.