开式简单布雷顿制冷循环热力学优化2.性能优化
张万里,罗 京,陈林根
(1.海军工程大学热科学与动力工程研究室舰船动力工程军队重点实验室动力工程学院,武汉 430033;2.中国卫星海上测控部,江苏江阴 214431)
本文第一部分利用开式循环优化原理[1-7]考虑工质的复杂流动过程,建立具有压降不可逆性的开式简单布雷顿制冷循环的热力学模型,导出压缩机耗功率、换热器换热率、膨胀机输出功率、排放到环境的乏气的放热率、制冷率和制冷系数及循环各个部件处由于工质的不可逆流动导致的压力损失与压缩机入口相对压力损失的函数关系,并对循环的热力学性能进行了分析。本部分将对循环的制冷率进行优化,并分析各种因素对制冷循环制冷率最优性能的影响;然后在循环输入功率、装置总的流通面积和换热器总的热导率一定条件下,以制冷系数最大为目标,优化沿工质流动路径的压降分配、各个部件流通面积的分配和换热器热导率的分配,并分析各种因素对优化结果的影响。
1 循环有关性能参数
根据本文第一部分的结果,循环有关参数具体如下。
压缩机无量纲输入功率为:
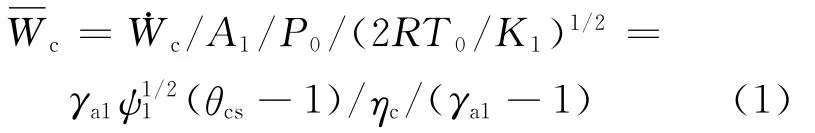
高温侧换热器无量纲换热率为:
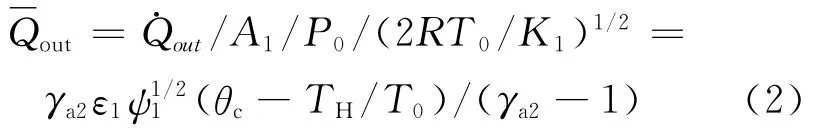
膨胀机无量纲输出功率为:
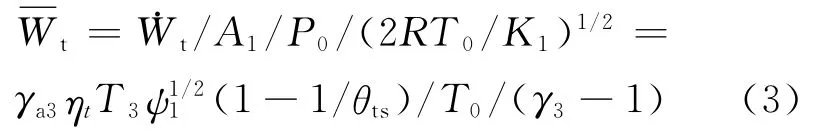
无量纲制冷率为:
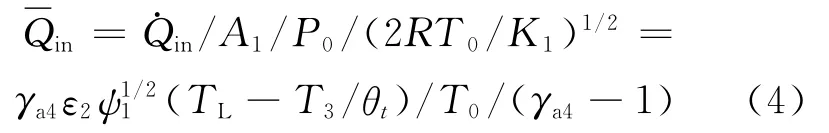
排放的乏气达到环境温度T0时的无量纲吸热率为:
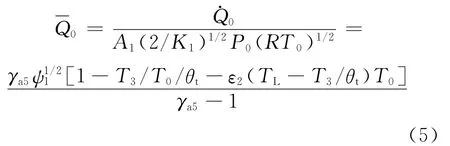
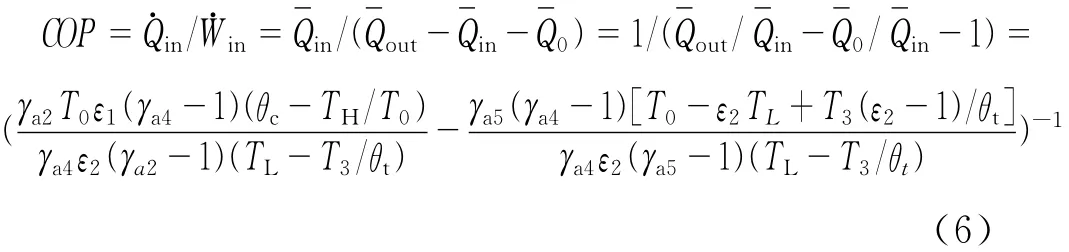
由于各个性能指标的表达式比较复杂,而且各个参数之间有着相互嵌套的关系(见图1),下面将用数值计算的方法来分析质量流率(或压降损失)对以上各性能指标的影响。计算时相关参数取值范围为:0≤ψ1≤0.2,2≤β1≤10,0.8≤ε1、ε2≤0.99;P0=0.101 3 MPa,ηc=0.9,ηt=0.85。计算时给定a1-3=1/2,a1-2=a1-4=a1-5=1/3,环境温度设为300 K。
2 开式简单布雷顿制冷循环的性能优化
设制冷空间温度为TL,为了方便对制冷循环进行分析,令TH=T0,定义热源温度比τ=TH/TL。
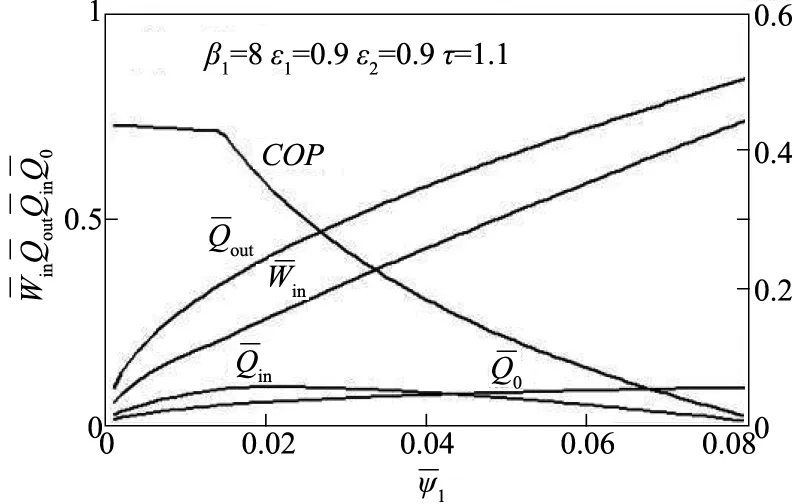
图1 -ψ1-ψ1-ψ1、和COP-ψ1特性关系
2.1 制冷率优化
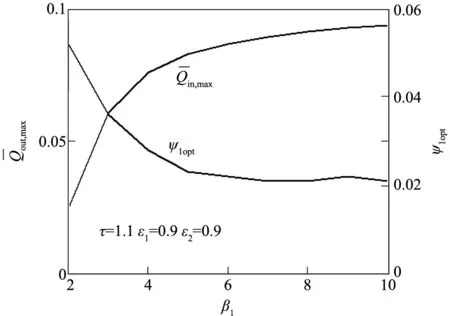
图2 -β1、ψ1opt-β1特性关系
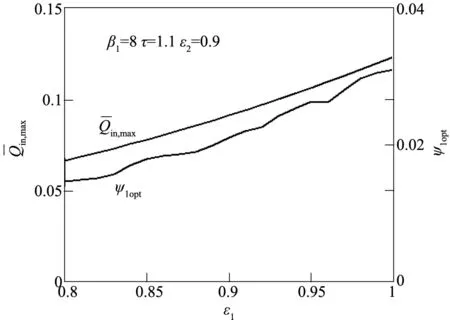
图3 -ε1、ψ1opt-ε1特性关系
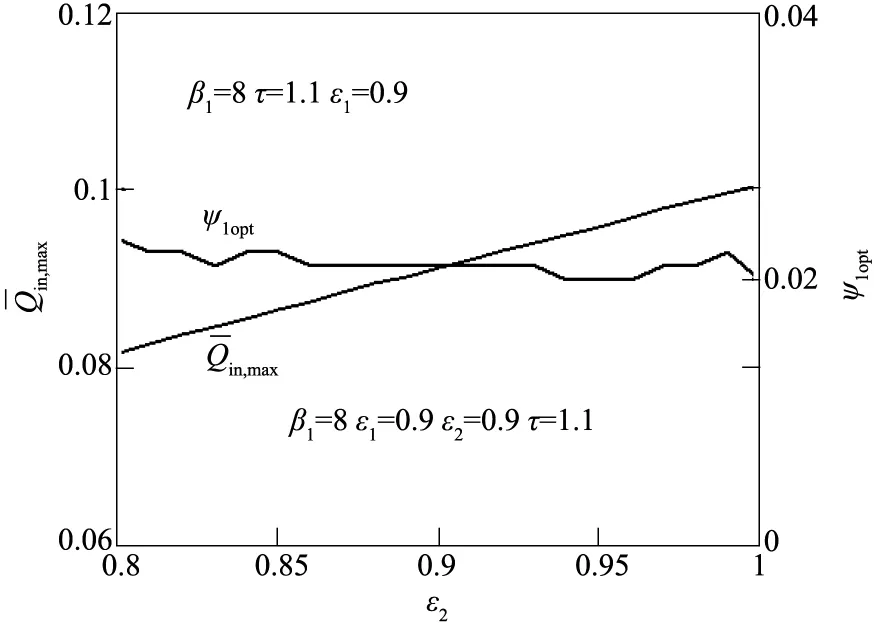
图4 ,max-ε2、ψ1opt-ε2特性关系
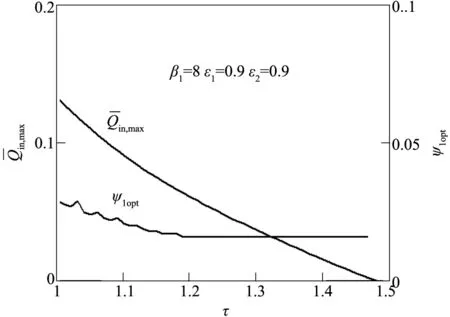
图5 ,max-τ、ψ1opt-τ特性关系
2.2 给定循环输入功率和装置尺寸时的制冷率优化
由图1可知,存在最佳压降(ψ1)opt使制冷率最大,但是当ψ1<(ψ1)opt时,(COP)ψ1>(COP)(ψ1)opt。实际上,当ψ1=0时,循环达到最大的制冷系数(COP)max,此时物理模型中说明的七项阻力引起的熵增均为零。实际应用中,制冷机的输入功率是给定的,因此物理模型有个输入功率约束,给定约束如下:
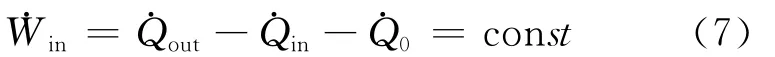
另外,循环装置总尺寸有限制。与总尺寸和重量相关的是压缩机、膨胀机和换热器的总尺寸。与压缩机和膨胀机总尺寸相关的是压缩机进口面积A1及膨胀机出口流通面积A4的总和A1+A4。这里为分析方便起见,以Ai/(i=2,3,4,5)代替Ai。令压缩机和膨胀机的尺寸约束如下:
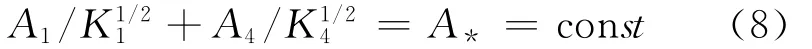
设循环中所用的换热器均为管道逆流式换热器,高温侧换热器管道直径为D1,管道长度为L1,管道数为nH,换热面积为F1,低温侧换热器管道直径为D2,管道长度为L2,管道数为nL,换热面积为F2,则高低温侧换热器工质的流通面积分别为:
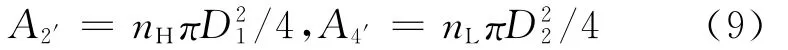
高低温侧换热器的换热面积分别为:
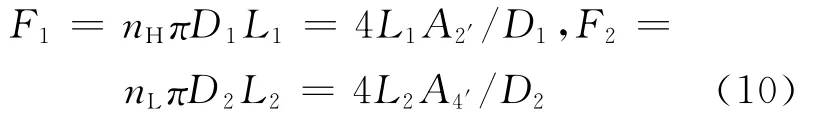
设高低温侧换热器的换热系数分别为κ1和κ2,则高低温侧换热器的热导率分别为:
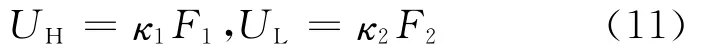
总热导率为:
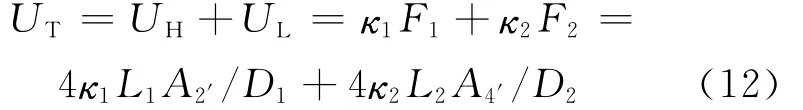
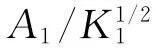
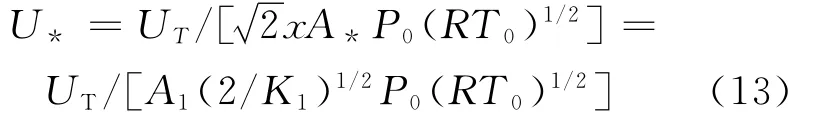
式中 U*为比例常数,U*由式(32)中的κ1、κ2、L1、L2、D1、D2及常数K2′和K4′确定。
设高温侧换热器的热导率为UH=u UT,则低温侧换热器的热导率为UL=(1-u)UT,这里u为热导率分配系数。则两个换热器的有效度分别变为:
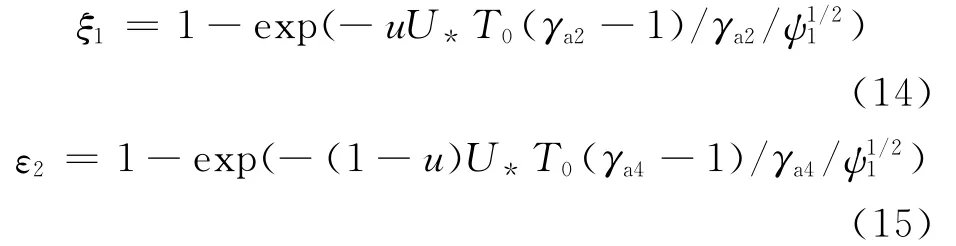
联立式(2)、式(4)、式(5)、式(7)和式(8)
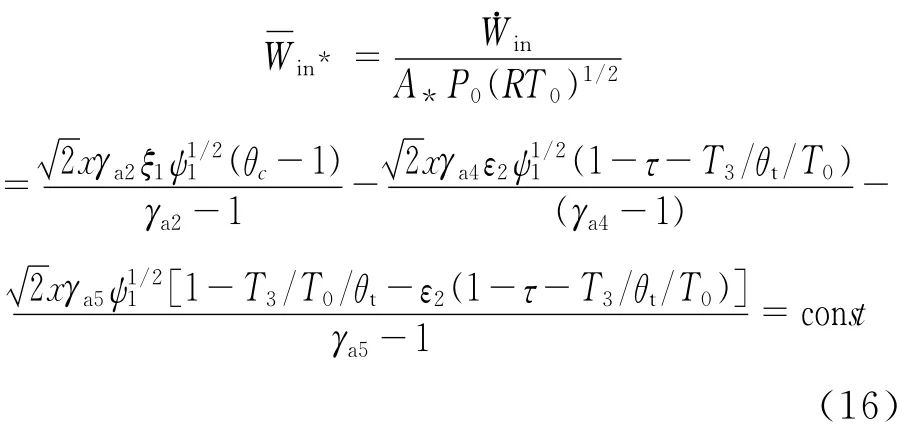
ψ2的表达式可改写为:
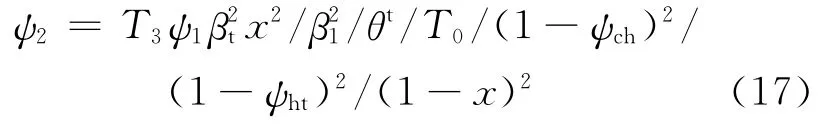
基于A*约束式(8),式(2)、(4)、(5)分别改写为:
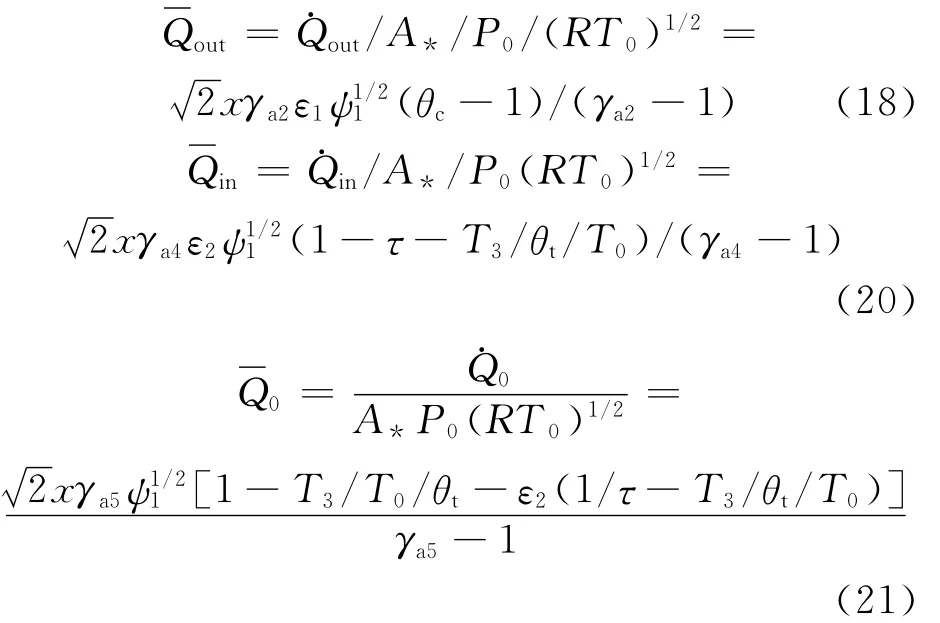
将式(18)至(21)代入式(6)可得改写的制冷系数为:
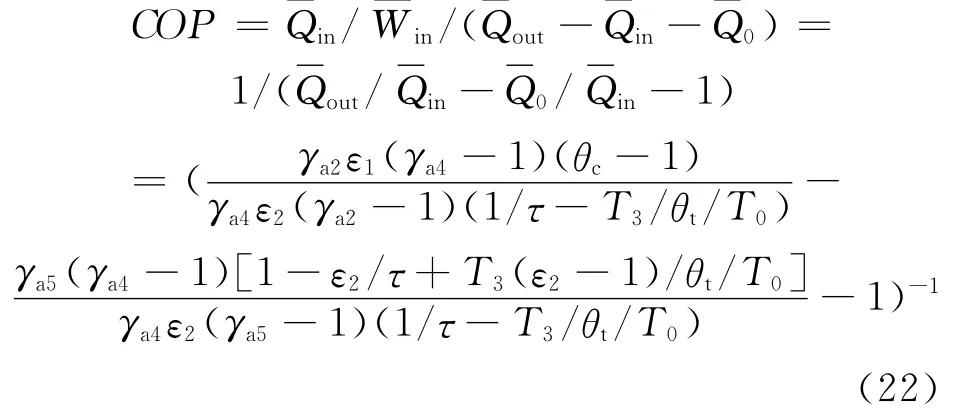
图6给出了制冷系数COP与压缩机入口相对压降ψ1、装置面积分配比x和换热器热导率分配系数u的变化关系。由图6可知,分别存在最佳的压缩机入口相对压降ψ1opt或装置面积分配比xopt和最佳的换热器热导率分配系数uopt使制冷系数COP取得最大值COPmax。
根据式(24),由下列方程组即可求出COPmax的数值解:
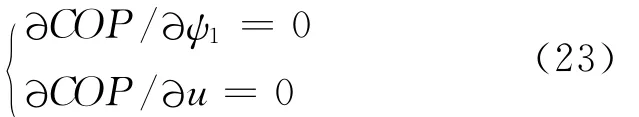
方程组求得的数值解见图7至图10。
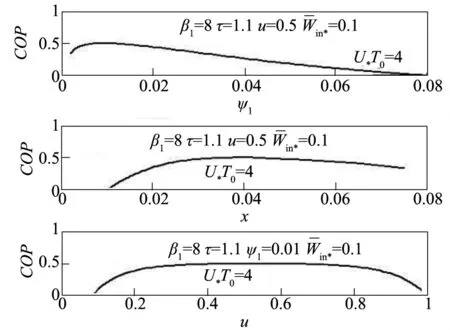
图6 COP-ψ1、COP-x、COP-u特性关系
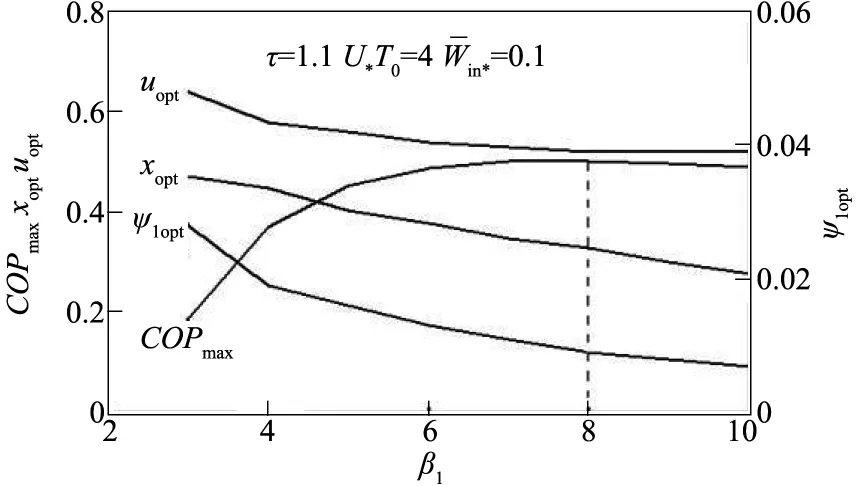
图7 COP max-β1、x opt-β1、u opt-β1和ψ1opt-β1特性关系
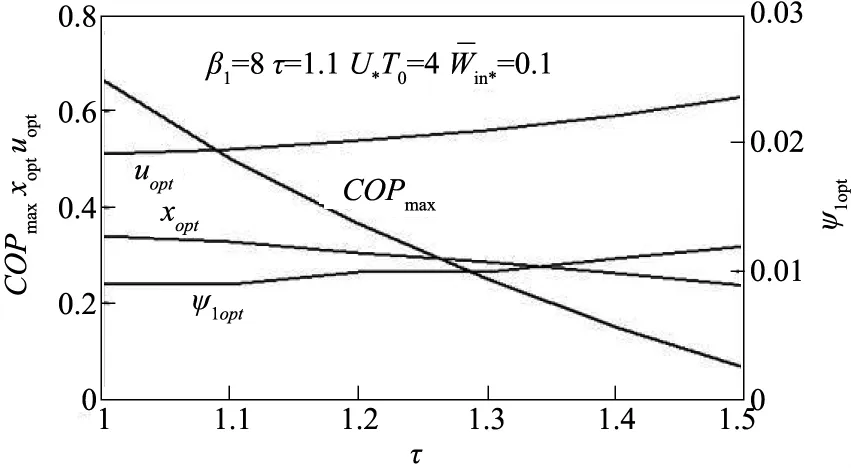
图8 COP max-τ、x opt-τ、u opt-τ和ψ1opt-τ特性关系
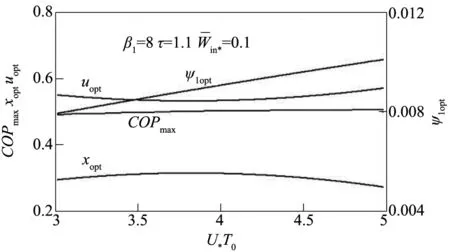
图9 COP max-U*T 0、x opt-U*T 0、u opt-U*T 0和ψ1opt-U*T 0特性关系
图7至图10分别给出了循环最大制冷系数COPmax及相应的压缩机入口最佳相对压降ψ1opt、最佳装置面积分配比xopt和最佳的换热器热导率分配系数uopt随压缩机压比β1、热源温度比τ、无量纲数U*T0和循环输入功率的变化关系。由图7可知,存在最佳的压缩机压比β1opt使COPmax取得附加最大值;由图7~10可知,COPmax随τ和增大而减小,随U*T0基本不变;ψ1opt随β1增大而减小,随τ、U*T0和增大而增大;xopt随β1和τ增大而减小,随增大而增大;uopt随β1增大而减小,随τ和增大而增大。
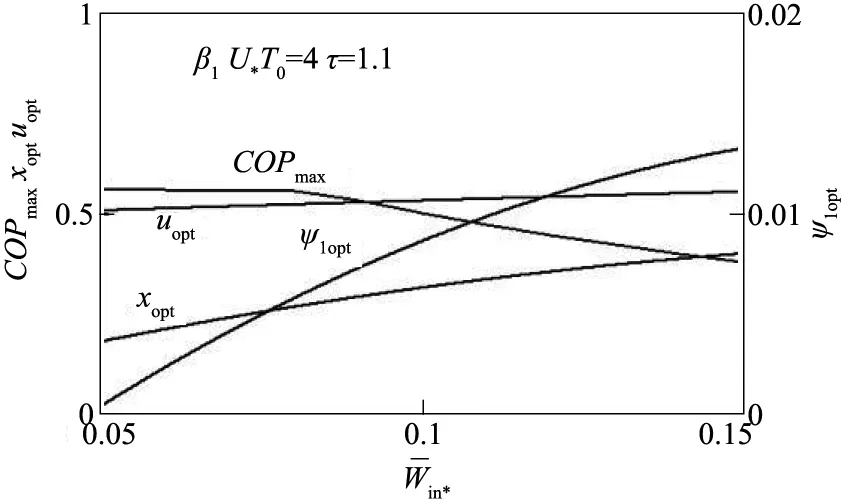
图10 COP max-、x opt-、u opt-和ψ1opt-特性关系
3 结论
本文开拓了开式简单制冷循环的研究,建立了开式简单空气制冷循环的热力学模型,导出了制冷率和制冷系数等性能参数与压缩机进口相对压降的函数关系,分别给出了空气制冷循环制冷率分析和优化结果,在输入功率、装置总的流通面积和总的热导率约束条件下制冷系数分析和优化的数值计算结果。研究结果表明,存在最佳的压缩机入口压降使制冷循环时的制冷率最大;当给定循环输入功率和装置总尺寸时,存在压缩机最佳入口压降使制冷循环时的制冷系数(制冷率)最大,存在最佳的高低温侧换热器热导率分配使制冷系数最大;最大制冷系数(制冷率)对压缩机压比有最大值。
[1]BEJAN A.Advanced Engineering Thermodynamics[M].New York:Wiley,1988.
[2]RADCENCO V.Generalized Thermodynamics[M].Bucharest:Editura Techica,1994.
[3]CHEN L,WU C,SUN F,et al.Performance characteristic of fluid flow converters[J].J.Instit.Energy,1998,71(489):209-215.
[4] BEJAN A,DAN N.Maximum power from fluid flow[J].Int.J.Heat Mass Transfer,1996,39(6):1175-1181.
[5]CHEN L,BI Y,WU C.Influence of nonlinear flow resistance relation on the power and efficiency from fluid flow[J].J.Phys.D:Appl.Phys.,1999,32(12):1346-1349.
[6] HU W,CHEN J.General performance characteristics and optimum criteria of an irreversible fluid flow system[J].J.Phys.D:Appl.Phys.,2006,39(5):993-997.
[7]KAZAKOV V A,BERRY R S.Estimation of productivity,efficiency,and entropy production for cyclic separation processes with a distributed working fluid[J].Phys.Rev.E,1994,49(4):2928-2934.

