华东地区城市供电可靠性增长模型的研究与应用
赵 彬,张 焰
(1.上海交通大学,上海 200240;2.国网上海市电力公司市北供电公司,上海 200072)
伴随着我国的经济发展和城市化进程,电力供应已经成为国民经济建设的重要支撑。而供电系统可靠性作为电力可靠性管理的重要组成部分,对确保电力的可靠供应有着十分重大的积极意义。供电系统可靠性不仅能够直接体现供电系统对用户的供电能力,更是反映电力工业的发展与国民经济电能需求是否匹配的重要指标[1]。可靠性增长的定义为“以产品的可靠性量度随时间逐步提供为特征的一种过程”[2]。电力可靠性管理的重要目标之一就是促进供电可靠性的增长。文献[3,4]中介绍了发电机组和输变电设施的可靠性增长模型,但是关于供电系统可靠性增长模型研究的公开文献还比较少。以华东地区四省一市的城市供电可靠性为例,研究城市供电可靠性的增长模型和预测方法,对于保障城市供电可靠性增长有积极意义。
1 供电系统可靠性的增长模型
1.1 供电系统可靠性的评价指标
对供电系统可靠性进行衡量和评价的主要评价指标为供电可靠率RS1和不计系统电源不足限电的供电可靠率RS3[1],根据DL/T836,RS1和RS3的表达式分别为
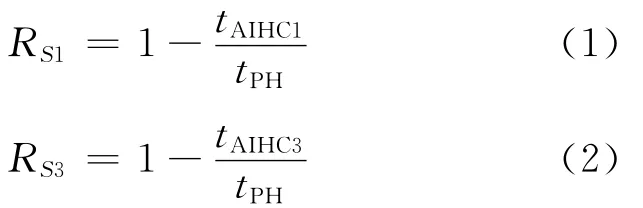
式中 tAICH1——用户平均停电时间;
tAICH3——不计系统电源不足限电的用户平均停电时间;
tPH——统计期间小时数。
1.2 检修系数的计算公式
为了研究供电可靠性的变化规律,本文引入供电系统检修系数ρR1和ρR3作为供电系统可靠性新的可靠性评价指标,其中对应RS1的检修系数ρR1的计算公式为

对应RS3的检修系数ρR3的计算公式为
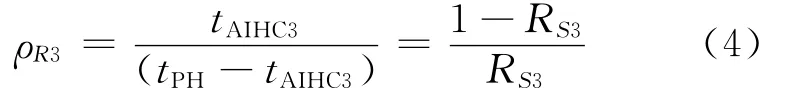
利用ρR1和ρR3的计算公式,供电可靠率RS1和RS3的可以表示为

1.3 检修系数的时间函数
在配电网日益坚强,供电可靠性有所改进的情况下,供电可靠率RS1和不计系统电源不足限电情况下的供电可靠率RS3以及其相应的检修系数ρR1和ρR3,可以处理为时间t的函数。在时间为第ti年时,检修系数ρR1(ti)、ρR3(ti)可表达为

式中 RS1(ti)、RS3(ti)——第ti年RS1、RS3的统计值。
1.4 建立供电系统可靠性的增长模型
受发电机组和输变电设备的可靠性增长模型启发[3,4],建立供电系统可靠性的增长模型表示为

式中 α1——ρR1增长模型的增长参数;
β1——ρR1增长模型的尺度参数;
α3——ρR3增长模型的增长参数;
β3——ρR3增长模型的尺度参数。
α1(或α3)的物理意义是能够将供电可靠性的增长情况通过定量表示出来。当α1(或α3)<0时,表明供电系统的可靠性在逐渐减小;当α1(或α3)=0时,ρR1(t)(或ρR3(t))为常数,表明供电系统的可靠性不变;当α1(或α3)>0时,表明供电系统的可靠性在日益增长,当α1(或α3)的定量越大,供电系统可靠性的增长速度就越快。
将式(9)、式(10)分别代入式(7)、式(8),供电系统可靠性的增长模型RS1和RS3可以表示为

将t=1代入式(9)和式(11),可得ρR1(t)=β1,RS1=(1+β1)-1。由此可以看出,尺度参数β1的物理意义反映了在可靠性增长初期t=1时,供电系统可靠性检修系数ρR1的基础水平;而(1+β1)-1反映了在可靠性增长初期t=1时,供电系统的可靠性RS1的基础水平。
同理,尺度参数β3的物理意义反映了在可靠性增长初期t=1时,供电系统可靠性检修系数ρR3的基础水平;而(1+β3)-1反映了在可靠性增长初期t=1时,供电系统的可靠性RS3的基础水平。
1.5 供电系统可靠性增长模型相关参数的估算
由式(9)和式(10)可以看出,ρR1(t)与ρR3(t)都是时间t的幂函数,其增长参数α1、α3和尺度参数β1、β3可以使用非线性回归的方法确定。考虑到变量t和ρ(t)在双对数坐标纸上具有线性关系,因此其尺度参数β1、β3与增长参数α1、α3可以通过最小二乘法来求出,换算步骤如下
对式(9)和(10)两边取对数,可得

令y=lnρR1(t),z=lnρR3(t),x=ln t,
a=lnβ1,b=-α1,c=lnβ3,d=-α3,则有

在式(15)与(16)中代入供电系统可靠性的统计数据后,可得出ti和ρR1(ti)、ρR3(ti)的n组观测值数据[t1,ρR1(t1)],[t2,ρR1(t2)],…,[tn,ρR1(ti)]与[t1,ρR3(t1)],[t2,ρR3(t2)],…,[tn,ρR3(ti)]。
令xi=ln ti,yi=lnρR1(ti),zi=lnρR3(ti),由最小二乘法可以得出以下公式
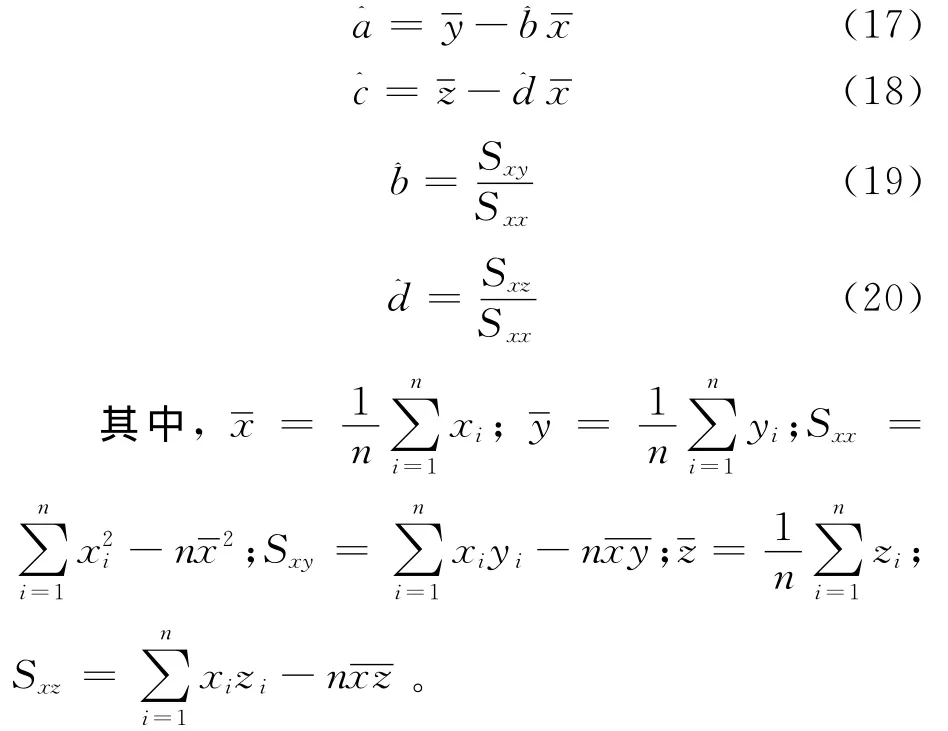
最后,可以得出式(9)和(10)中供电系统可靠性增长模型的增长参数α1与α3与尺度参数β1与β3的估计结果分别为
1.6 供电系统可靠性增长模型的统计检验
在建立供电可靠性增长模型的基础上,需根据相关的供电可靠性统计数据来检验供电可靠性增长规律是否与所建立的供电可靠性增长模型相符合。根据文献[5],采用统计检验法计算的检验统计量F1和F3的计算公式分别为
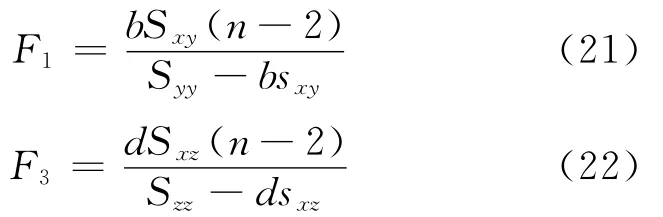
其中,

根据式(21)和式(22)计算得出的检验统计量F1和F3,可以判断供电系统可靠性的变化规律是否符合所建立的增长模型。通过给定一个显著性水平γ,结合F分布上侧分位数表[6],可以得出Fγ(1,n-2)。当F1>Fγ(1,n-2)或F3>Fγ(1,n-2)时,判断式(9)或式(10)中所建立的供电系统可靠性增长模型可以接受;当F1≤Fγ(1,n-2)或F3≤Fγ(1,n-2)时,判断式(9)或(10)中所建立的可靠性增长模型不能接受。
2 华东四省一市城市供电系统可靠性的增长分析
2.1 华东四省一市供电系统可靠性的统计分析
文献[7]中所提供的2005~2010年华东地区上海、江苏、浙江、安徽、福建等省市供电系统可靠性统计值RS1和RS3的数据进行统计汇总,如表1所示。表中上海、江苏、安徽和福建四地的城市供电可靠率RS1=RS3,其可靠性统计数据相一致,浙江城市供电可靠率RS1≠RS3。

表1 华东四省一市城市供电可靠性统计数据
利用表1中所列华东地区四省一市的城市供电可靠性数据,可以计算出本文所建立的供电系统可靠性增长模型的尺度参数β与增长参数α,以及其校验统计量F,具体数值见表2。
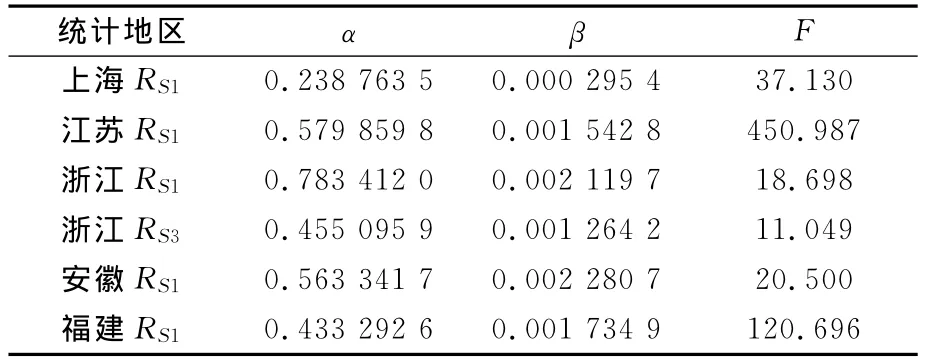
表2 华东四省一市城市供电可靠性增长模型参数
查F分布上侧分位数表[6],可得Fγ(1,n-2)=F0.1(1,4)=4.54。由表2可见,华东四省一市城市供电可靠性增长模型的检验统计量F的最小值为Fmin=11.049>4.54。由此判断,本文所建立的供电可靠性增长模型式(9)、式(10)与华东地区四省一市的城市供电可靠性增长规律相符。同时,由于华东地区各省市增长参数α>0,表明华东地区四省一市对于配电网的改造和升级取得了较好成效,近年来该地区城市供电系统的可靠性正在呈增长趋势。
2.2 华东四省一市城市供电可靠性的预测
使用根据2005~2010年华东地区四省一市城市RS1和RS3的统计数据得出的城市供电可靠性增长参数α和尺度参数β,可以用来预测2011~2012年华东地区四省一市城市RS1和RS3。采用表2中所给出的城市供电可靠性增长模型参数,将其值代入式(11)和式(12)中,可以得出以下华东地区四省一市的城市供电系统可靠性增长模型。
上海市供电可靠性增长模型的主要特征量RS1=RS3为
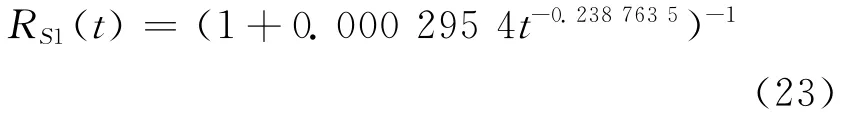
江苏省供电可靠性增长模型的主要特征量RS1=RS3为

浙江省供电可靠性增长模型的主要特征量RS1为
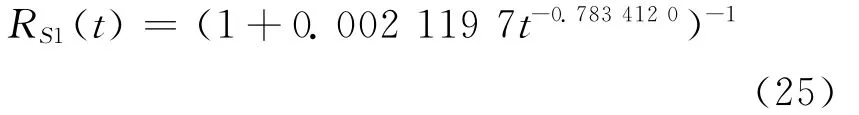
浙江省供电可靠性增长模型的主要特征量RS3为

安徽省供电可靠性增长模型的主要特征量RS1=RS3为

福建省供电可靠性增长模型的主要特征量RS1=RS3为

为了分析本文建立的华东地区城市供电可靠性增长模型的预测精度,根据公式(23)~式(28)分别计算2011、2012年上海、江苏、浙江、安徽、福建等地的城市供电可靠率RS1与RS3,并将计算结果与文献[8]中所给出的2011~2012年华东四省一市RS1与RS3的实际统计值相比较,比较结果如表3所示。表3中,相对误差计算公式为

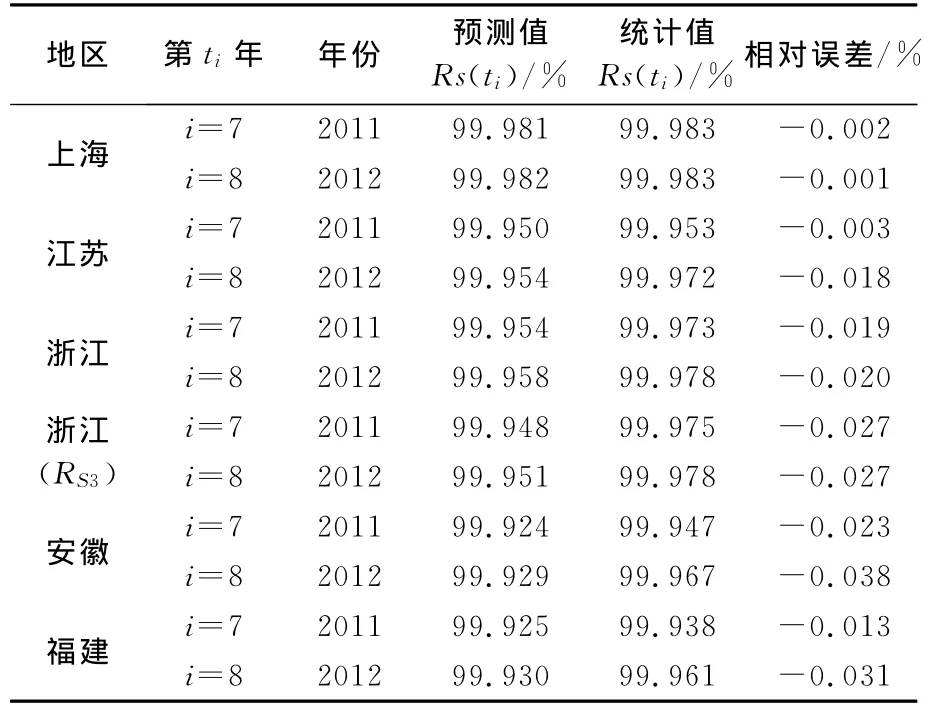
表3 华东地区供电可靠性增长模型的预测精度
由表3可见,本文建立的华东地区四省一市的城市供电可靠性增长模型所预测的2011、2012年供电可靠性特征量RS1、RS3,其数值与实际统计值基本一致,相对误差绝对值在0.038%以下,具有比较高的预测精度与比较好的实用性。
2.3 华东四省一市城市供电可靠性的增长趋势
近年来,伴随着配电网设施的强化以及电力公司服务意识的增强,华东地区四省一市的城市供电可靠性呈逐年上升的态势。采用本文式(23)~式(28)所得出的增长模型,分别对上海、浙江、江苏、安徽、福建等四省一市的2013~2018年城市供电可靠性进行预测,其增长变化趋势如图1~图6所示。
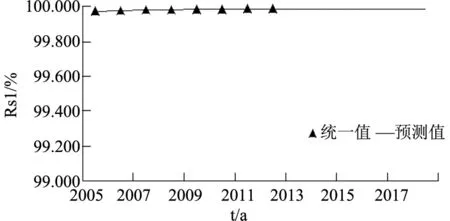
图1 上海供电系统可靠性的变化趋势(RS1=RS3)
根据图1~图6所绘出的华东地区各省市城市供电可靠性的变化趋势图,可以看出由本文建立的供电系统可靠性增长模型计算得出的上海、江苏、浙江、安徽、福建等四省一市城市的RS1、RS3预测值,与实际统计值的增长规律基本相符,并呈逐年上升的趋势。
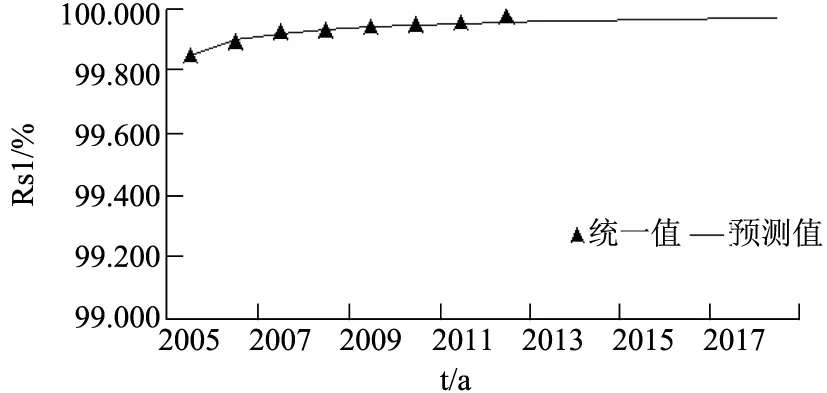
图2 江苏供电系统可靠性的变化趋势(RS1=RS3)

图3 浙江供电系统可靠性RS1的变化趋势
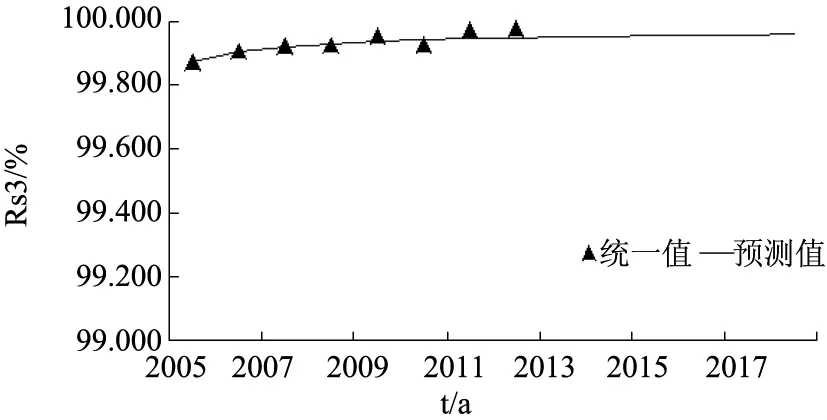
图4 浙江供电系统可靠性RS3的变化趋势
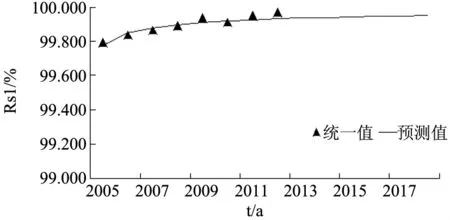
图5 安徽供电系统可靠性的变化趋势(RS1=RS3)

图6 福建供电系统可靠性的变化趋势(RS1=RS3)
3 结语
文中所建立的供电系统可靠性增长模型,与华东地区四省一市的城市供电可靠性增长规律相符合。使用供电系统可靠性增长模型得出的2011~2012年华东四省一市城市供电可靠性的预测值与实际统计值相符合,相对误差比较小。
使用本文建立的供电系统可靠性增长模型,结合华东地区历年发布的可靠性统计数据,对上海、江苏、浙江、安徽、福建等四省一市的城市供电可靠性变化趋势进行了可靠性增长分析,结果表明上述地域城市供电可靠性呈上升趋势。
[1] DL/T836-2012供电系统用户供电可靠性评价规程[S].
[2] GB/T2900.13—2008电工术语可信性与服务质量[S].
[3] 史进渊,杨 宇,危奇.大型火电设备可用性评定新技术[J].机械工程学报,2005,41(7):205-210.SHI Jin-yuan,YANG Yu,WEI Qi.New technology for availability assessment of large capacity thermal power equipments[J].Chinese Journal of Mechanical Engineering,2005,41(7):205-210.
[4] 史 清.输变电设备可靠性增长模型及其在220 k V输变电设备中的应用[J].能源技术经济,2012,24(1):38-41.SHI Qing.Reliability growth model of electric equipment and its application in 220 k V electric equipment[J].Electric Power Technologic Economics,2012,24(1):38-41.
[5] 方开泰,全 辉,陈庆云.实用回归分析[M].北京:科学出版社,1988.
[6] 中国电子技术标准化研究所.可靠性试验用表[M].北京:国防工业出版社,1987.
[7] 电力可靠性管理中心.中国电力可靠性管理年报[R].2005~2010.
[8] 电力可靠性管理中心.中国电力可靠性管理年报[R].2011~2012.

