开式简单布雷顿制冷循环热力学优化1.热力学建模

张万里，罗 京，陈林根

（1.海军工程大学热科学与动力工程研究室舰船动力工程军队重点实验室动力工程学院，武汉 430033；2.中国卫星海上测控部，江苏江阴 214431）

因布雷顿制冷循环的循环工质为无环境公害的空气，且其工作循环逆布雷顿循环具有典型热力学特性，不会对大气臭氧层造成破坏，实现了“绿色”制冷，故对其的研究近年来颇受学者们的重视。在联合国蒙特利尔协议已确定，2030年前在世界范围完全停止使用各类含氟制冷剂的规定下，曾遭忽视的布雷顿制冷循环研究又显现了曙光［1-6］。

有限时间热力学理论和方法［7－13］是研究和优化各种热力学循环和装置性能的有效工具。早期的研究主要是针对卡诺循环，随后又拓展到布雷顿循环。对于正反向布雷顿循环的研究中，主要以针对闭式循环的研究为主，对于开式循环的研究比较少，对于开式逆布雷顿循环的研究则更少，尚未发现公开发表的文献。比较正向布雷顿循环和逆布雷顿循环的工质流动过程可以发现，工质同样经过透平机械和换热器，有着与这些设备相关的类似的流动机理。由于对工质流动过程较复杂循环的研究主要就是考虑工质的流动机理，故对于开式逆布雷顿循环的研究与开式布雷顿循环的研究是类似的。Radcenco等［14］对开式单轴简单燃气轮机循环的功率效率进行了分析与优化。陈林根等［15］等对开式回热燃气轮机循环的功率进行了分析与优化。王文华等［16］对开式中冷燃气轮机循环的功率效率进行了分析与优化。陈林根等［17，18］对三轴开式中冷回热燃气轮机循环的功率效率进行了分析与优化，并进一步分析了该模型的生态学函数性能［19，20］。张万里等［21－23］对开式布雷顿、（两平行）逆布雷顿循环的功率和效率进行了分析与优化。张万里等［24］建立了开式微型燃气轮机外燃循环的热力学模型。张万里等［25，26］研究了采用布雷顿制冷循环冷却压气机进气的开式燃气轮机循环的功率效率特性。本文将利用开式循环优化原理［27－33］考虑工质的复杂流动过程，建立具有压降不可逆性的开式简单布雷顿制冷循环的热力学模型，导出压缩机耗功率、换热器换热率、膨胀机输出功率、排放到环境的乏气的放热率、制冷率和制冷系数及循环各个部件处由于工质的不可逆流动导致的压力损失与压缩机入口相对压力损失的函数关系，并对这些参数进行分析。

1 物理模型

考虑如图1所示的逆布雷顿循环装置示意图，其T-s图如图2所示。工质分别流过压缩机、高温侧换热器、膨胀机和低温侧换热器时，都存在压降。研究的关键是确定是否存在最佳压降（或最佳流率），使得循环性能最优。

考虑工质流动过程的实际情况，作以下建模假设。

（1）循环工质（空气）为理想气体，其比热仅随温度和成分变化。

（2）空气不可逆的进入压缩机（过程0—1），存在压力损失ΔP1＝P0－P1，环境条件T0下的比熵增为Δs1。

（3）空气不可逆绝热压缩的熵增为Δsc（过程1—2）。在图2中简化为等熵线1—2s′，和节流过程2s′—2。由于摩擦引起的工质压力损失为ΔPc。

（4）空气流经高温侧换热器（过程2—3′）引起压力损失ΔPch，该过程可简化为节流过程2— 2′（熵增Δs2），等压放热过程2′—3′（压力P′）。因摩擦引起的工质压力损失为ΔPch。热泵循环时，TH为供热空间温度。

图1 开式简单制冷循环压降和质量流率分配图

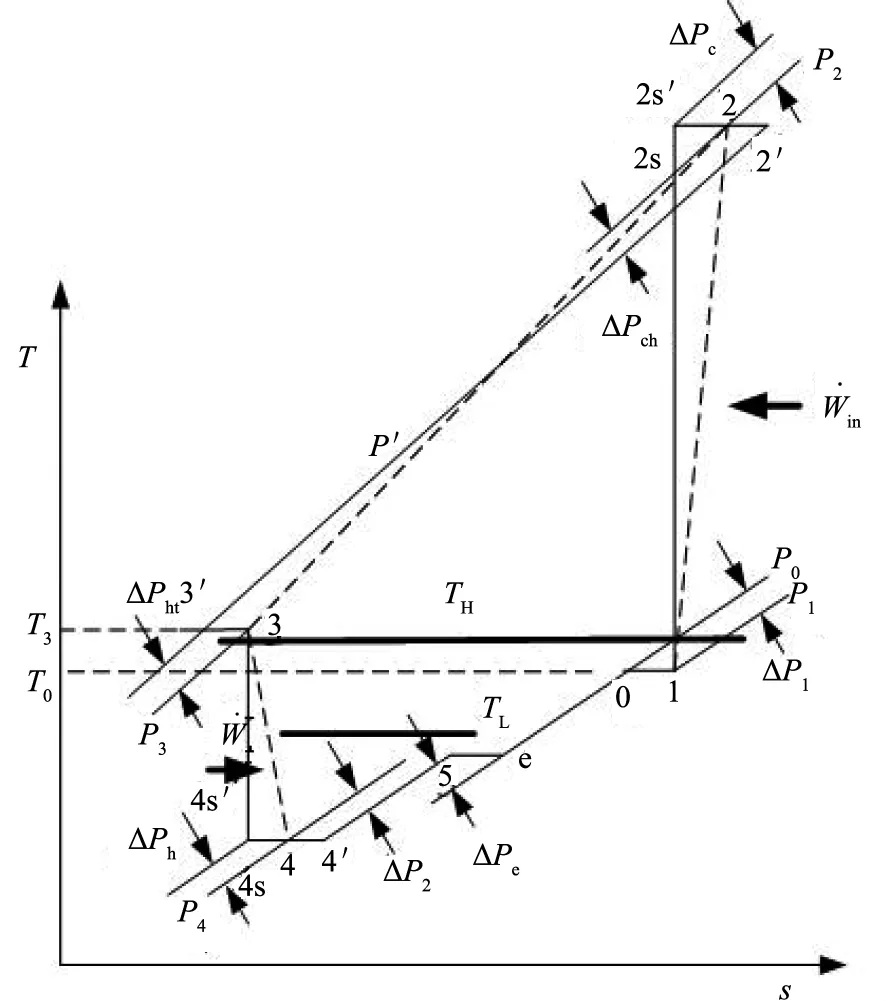
图2 开式简单制冷循环T-s及流阻图

（5）工质不可逆进入膨胀机（过程3′—3），引起压力损失ΔPht，熵增Δs3。

（6）不可逆绝热膨胀过程3—4的工质熵增Δst，可简化为沿等熵过程3—4s′，后节流过程4s′—4，通过膨胀机因摩擦引起的工质压力损失为ΔPt。

（7）工质流经低温侧换热器（过程4—5）引起的压力损失为ΔP2，该过程可简化为工质流入换热器的节流过程4—4′（熵增为Δs4），后经等压吸热过程4′—5。工质通过换热器因摩擦引起的压力损失为ΔP2。制冷循环时，TL为制冷空间温度。

（8）低温侧换热器中工质流出过程5—e的压力损失为ΔPe＝P5－P0，在温度Te下的熵增为Δse。

2 热力学分析

工质在流动过程中要遇到七种流动阻力，如图2所示。工质通过压缩机、膨胀机时所受摩擦力大小与等熵效率ηe和ηt相关。实际上，如果等熵效率（ηc，ηt）→1时，摩擦力可以忽略不计。但由于压缩机等设备进出口出截面积的变化导致工质状态的不可逆变化，流动阻力不可忽略。而阻力决定了质量流率。可用下式表示进入压缩机的压力损失：

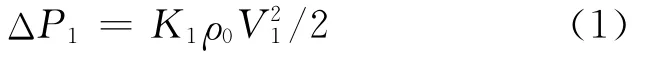
式中 K1——压力损失系数；V1——入口截面A1处的平均空气流速，如图2所示。

假设工质为高紊流态，取第一级近似，入口截面积取常量时K1也可取常数［34］。通过同一截面质量流率＝A1ρ0V1，另写为：

式中 ψ1——流动阻力决定的压气机入口的相对压力损失，ΨΔP1／P0。

该过程工质的比热比为：

式中 R——气体常数，R＝0.287 kJ／（kg·k）。

则，比热比γa1可以由式（5）确定。

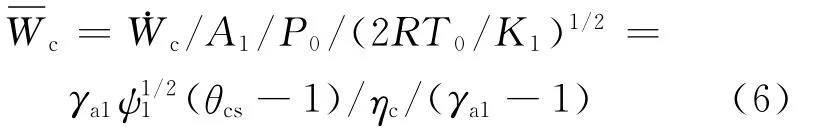
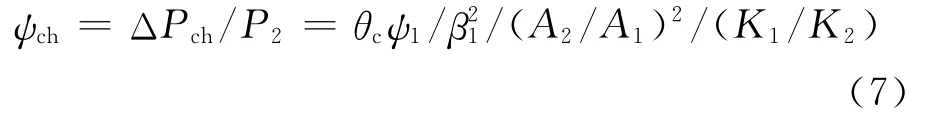
由工质性质和热源与工质间的传热可得高温侧换热器换热率为：

式（8）中γa2由式（5）确定。ε1为高温侧换热器有效度：

式中 NH——传热单元数，NH＝UH／）；UH——工质与高温热源间的热导率。

由式（8）可得：

工质放热后进入膨胀机，压力损失为ΔPht＝K3ρ3／2，相对压力损失为ψht＝ΔPht／P′。其中K3为压力损失系数，当常数处理，V3为空气流入膨胀机入口截面A3时的平均速率。根据质量守恒＝A1ρ0V1＝A3ρ3V3，可得相对压力损失为：

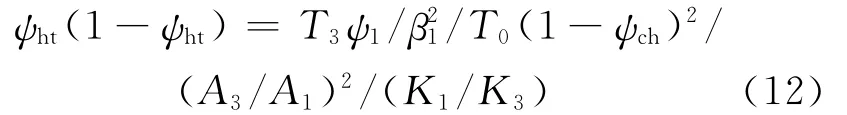
膨胀机输出比功为wt＝ηtRT3（1－1／θts）γa3／（γa3－1），它与叶片流动压力损失有关。注意到h4s′＝h4，ψt＝ΔPt／P4＝（θts／θt）γa3／（γa3－1）－1，θt＝T3／T4＝（1－ηt＋ηt／θts）－1，膨胀机输出功率为＝mwt，则无量纲输出功率可定义为：

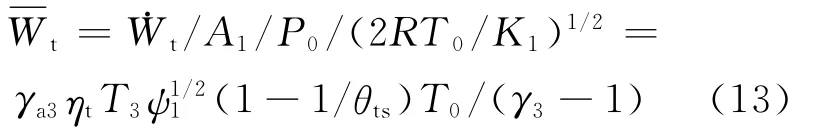
工质离开膨胀机进入换热器2的压力损失为ΔP2＝K4ρ4／2，其中K4为压力损失系数，V4为膨胀机出口截面A4处的平均速率。根据质量守恒可得＝A1ρ0V1＝A4ρ4V4，膨胀机排气相对压力损失为：

由工质性质和热源与工质间的传热可得制冷率为：

式（15）中，γa4由式（5）确定，ε2为低温侧换热器有效度：

式中 NL——传热单元数，NL＝UL／（）；UL——工质与低温热源间的热导率。

由式（15）可得：

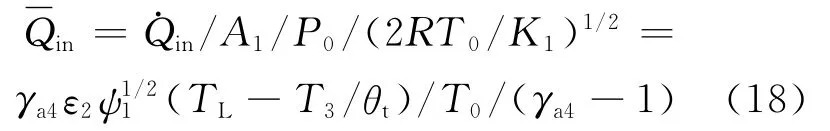
换热器2出口的压力损失用大气压力来定义，ΔPe＝K5ρ5／2，其中K5为压力损失系数，V5为换热器2出口截面A5处的平均速率。压气机排气相对压力损失ψ5＝ΔPe／P0，排气口出压力为P5＝P0（1＋ψ5）。根据流动的连续性有m·＝A1ρ0V1＝A5ρ5V5，经推导可得到

则，膨胀机膨胀比为：

式中 γa5由式（5）确定。

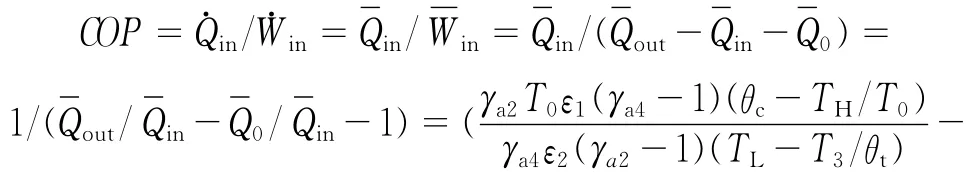
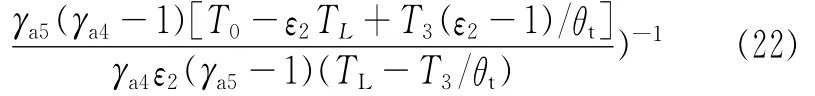
以上相关参数取值范围为：0≤ψ1≤0.2，2≤β1≤10，0.8≤ε1、ε2≤0.99；P0＝0.101 3 MPa，ηc＝0.9，ηt＝0.85。两端流动的等效截面积之比的范围为0.25≤a1－i≤4，这里a1－i为无量纲数组：

计算时给定a1－3＝1／2，a1－2＝a1－4＝a1－5＝1／3，环境温度设为300 K。

3 开式简单布雷顿制冷循环的性能分析

设制冷空间温度为TL，为了方便对制冷循环进行分析，令TH＝T0，定义热源温度比τ＝TH／TL。

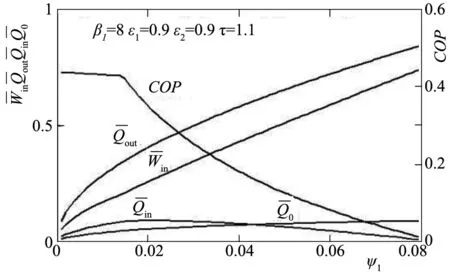
图3 －ψ1－ψ1－ψ1－ψ1和COP－ψ1特性关系

4 结语

本文建立了考虑压降不可逆性的开式简单布雷顿制冷循环的热力学模型，导出了制冷率和制冷系数等性能参数与压缩机进口相对压降的函数关系。函数表达式表明，压缩机消耗功率（式（6））、高温侧换热器换热率（式（11））、膨胀机输出功率（式（13））、制冷率（式（18））和排气损失引起的热流率（式（21））都与成正比，因此与质量流率也成正比，即能量交换率in和均随着质量流率成正比减少，如质量流率为零时，放热率和吸热率均为零。

另外，对简单布雷顿制冷循环各参数的无量纲量的分析得出，存在最佳的压缩机进口相对压降使循环制冷率最大。

［1］HAMLIN S，HUNT R，TASSOU S A.Enhancing the performance of evaporative spray cooling in air cycle refrigeration and air conditioning technology［J］.Appl.Therm.Engng.，1998，18（9）：1139-1148.

［2］SPENCE S W T，DORAN W J，ARTT D W.Design，construction and testing of an air-cycle refrigeration system for road transport［J］.Int.J.Refrig.，2003，27（5）：503–510.

［3］ WILLIAMSON N J，BANSAL P K.Feasibility of air cycle systems for low temperature refrigeration applications with heat recovery［J］.Proc.IMech E，Part E，J.Process Mech.Eng.，2003，217（E3）：267–273.

［4］SPENCE S W T，DORAN W J，ARTT D W.Performance analysis of a feasible air-cycle refrigeration system for road transport［J］.Int.J.Refrig.，2004，28（3）：381-388.

［5］FLEMING J S，VAN DER WEKKEN B J C，MCGOVERN J A，et al.Air-cycle cooling and heating，Part 1：A realistic appraisal and a chosen application［J］.Int.J.Energy Res.，1998，22（7）：639-55.

［6］FLEMING J S，LI L，VAN DER WEKKEN B J C.Aircycle cooling and heating，Part 2：A mathematical model for the transient behaviour of fixed matrix regenerators［J］.Int.J.Energy Res.，1998，22（5）：463-76.

［7］BEJAN A.Entropy Generation through Heat and Fluid Flow［M］.New York：Wiley，1982.

［8］SIENIUTYCZ S，SALAMON P.Advances in Thermodynamics.Volume 4：Finite Time Thermodynamics and Thermoeconomics［M］.New York：Taylor ＆Francis，1990.

［9］BERRY R S，KAZAKOV V A，SIENIUTYCZ S，et al.Thermodynamic Optimization of Finite Time Processes［M］.Chichester：Wiley，1999.

［10］GORDON J M，NG K C.Cool Thermodynamics［M］.Cambridge：Cambridge Int.Science Publishers，2000.

［11］ 陈林根.不可逆过程和循环的有限时间热力学分析［M］.北京：高等教育出版社，2005.

［12］SIENIUTYCZ S，JEZOWSKI J.Energy Optimization in Process Systems［M］.Oxford：Elsevier，2009.

［13］FEIDT M.Optimal thermodynamics-New upperbounds［J］.Entropy，2009，11（4）：529-547.

［14］RADCECO V，VARGAS J V C，BEJAN A.Thermodynamic optimization of a gas turbine power plant with pressure drop irreversibilities［J］.Trans.ASME，J.Energy Res.Techn.，1998，120（3）：233-240.

［15］CHEN L，LI Y，SUN F，et al.Power optimization of open-cycle regenerator gas-turbine power plants［J］.Appl.Energy，2004，78（2）：199-218.

［16］WANG W，CHEN L，SUN F，et al.Performance optimization of an open-cycle intercooled gas turbine power plant with pressure drop irreversibilities［J］.J.Energy Instit.，2008，81（1）：31-37.

［17］WANG W，CHEN L，SUN F.Thermodynamic optimization of a triple-shaft open intercooled-recuperated gas turbine cycle.Part 1，Description and modeling［J］.Rev.Mex.Fis，in press.

［18］WANG W，CHEN L，SUN F.Thermodynamic optimization of a triple-shaft open intercooled-recuperated gas turbine cycle.Part 2，Power and efficiency optimization［J］.Rev.Mex.Fis，in press.

［19］WANG W，CHEN L，SUN F.Ecological performance optimization for an open-cycle ICR gas turbine power plant.Part 1：Thermodynamic modeling［J］.J.Energy Insit.，in press.

［20］WANG W，CHEN L，SUN F.Ecological performance optimization for an open-cycle ICR gas turbine power plant.Part 2：Optimization［J］.J.Energy Insit.，in press.

［21］ZHANG W，CHEN L，SUN F.Power and efficiency optimization for combined Brayton and inverse Brayton cycles［J］.Appl.Therm.Engng.，2009，29（14-15）：2885-2894.

［22］CHEN L，ZHANG W，SUN F.Power and efficiency optimization for combined Brayton and two parallel inverse Brayton cycles，Part 1：Description and modeling［J］.Proc.IMechE，Part C：Mechanical Engineering Science，2008，222（C3）：393-403.

［23］ZHANG W，CHEN L，SUN F.Power and efficiency optimization for combined Brayton and two parallel inverse Brayton cycles，Part 2：Performance optimization［J］.Proc.IMechE，Part C：Mechanical Engineering Science，2008，222（C3）：405-414.

［24］CHEN L，ZHANG W，SUN F.Thermodynamic optimization for an open cycle of externally fired micro gas turbine（EFmGT）.Part 1：Thermodynamic modeling［J］.Int.J.Sustainable Energy，2011，30（4）：246-256.

［25］CHEN L，ZHANG W，SUN F.Performance optimization for an open cycle gas turbine power plant with a refrigeration cycle for compressor inlet air cooling.Part 1：Thermodynamic modeling［J］.Proc.IMech E，Part A：J.Power Energy，2009，223（A5）：505-513.

［26］ZHANG W，CHEN L，SUN F.Performance optimization for an open cycle gas turbine power plant with a refrigeration cycle for compressor inlet air cooling.Part 2：Power and efficiency optimization［J］.Proc.IMechE，Part A：J.Power Energy，2009，223（A5）：515-522.

［27］BEJAN A.Advanced Engineering Thermodynamics［M］.New York：Wiley，1988.

［28］RADCENCO V.Generalized Thermodynamics［M］.Bucharest：Editura Techica，1994.

［29］CHEN L，WU C，SUN F，et al.Performance characteristic of fluid flow converters［J］.J.Instit.Energy，1998，71（489）：209-215.

［30］BEJAN A，DAN N.Maximum power from fluid flow［J］.Int.J.Heat Mass Transfer，1996，39（6）：1175- 1181.

［31］CHEN L，BI Y，WU C.Influence of nonlinear flow resistance relation on the power and efficiency from fluid flow［J］.J.Phys.D：Appl.Phys.，1999，32（12）：1346-1349.

［32］HU W，CHEN J.General performance characteristics and optimum criteria of an irreversible fluid flow system［J］.J.Phys.D：Appl.Phys.，2006，39（5）：993-997.

［33］KAZAKOV V A，BERRY R S.Estimation of productivity，efficiency，and entropy production for cyclic separation processes with a distributed working fluid［J］.Phys.Rev.E，1994，49（4）：2928-2934.

［34］BEJAN A.Heat Transfer［M］.New York：Wiley，1993.

［35］GORDON C O.Aerodynamics of Aircraft Engine Components［M］.New York：AIAA Press，1985.

［36］MORAN M，SHAPIRO H.Fundamentals of Engineering Thermodynamics［M］.New York：Wiley，2004.