一道“北约”自主招生试题的另证

喻俊辉

（江西省九江一中）

2014 年“北约”自主招生考试中有这样一道不等式试题：

设正实数x1，x2，…，xn满足x1，x2，…，xn=1.证明：

如果尝试用归纳法来证明这个不等式，将会发现从n=k 过渡到n=k+1 比较困难，不好处理。然而，若将其强化为：

若x1，x2，…，xn为正实数，则

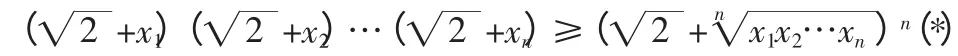
将会发现虽然从n=k 过渡到n=k+1 依然困难，但是由n=k 时命题成立推出n=k-1 时命题成立却是轻而易举的。那么，能否由此导出对任意的n≥2，n∈N+时（*）成立呢？结论是肯定的，其证明如下：

先用归纳法证明对于k∈N+时，（*）对n=2k成立

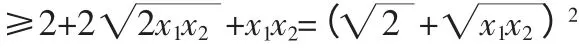
即（*）对n=21成立.

若命题对n=2k成立，则n=2k+1时，

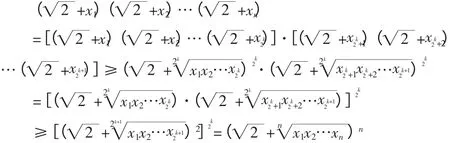
故（*）对n=2k+1也成立。由归纳原理，当k 取任意正整数时，（*）对n=2k成立。

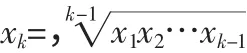
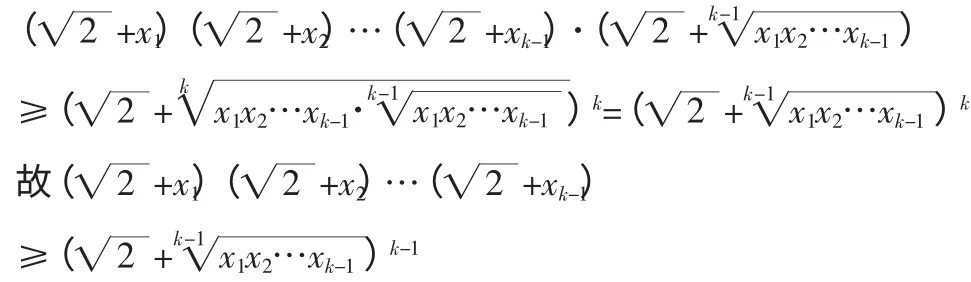
即（*）命题对n=k-1 成立；综上所述，由归纳原理，（*）对于一切不小于2 的正整数都成立。

这种先由n=21推到n=2k，再由n 推到n-1 的归纳法叫做反向归纳法。反向归纳法的使用在自主招生与竞赛中时常出现，它区别于一般归纳法，适用于从n=k 较难过渡到n=k+1，但是由n=k 命题成立推出n=k-1 时命题成立较易，且对于n=2k时命题的证明较简单。抓住这个特点很容易分辨哪些问题可以用反向归纳法来处理。

能用反向归纳法解决的问题特点非常鲜明，较易判断，用其他做法往往比较困难，有计划参加竞赛或自主招生的学生应加以掌握。