概念教学 回归本源——以方差概念及公式教学为例

史傲丽

（江苏省常州市第二十四中学天宁分校）

数学中概念是思维的基本形式，具有确定研究对象和任务的作用。概念课的教学应充分体现数学概念的产生、提炼过程。在概念的发现、形成、发展的过程中，让学生了解数学模型，体会数学理性，感受数学文化与背景。概念课的教学应该是“过程教学”，而不是告知式的“结果教学”。概念要避免形式单调的引入，避免学生根据老师的讲解进行模仿记忆和再训练的模式。在教学中我发现方差概念及公式的教学常常会陷入困境，仔细研究并实践，和各位交流一下。

在中学数学统计知识中有两类描述数据特征的概念，一类是描述数据集中程度的，如平均数、中位数、众数；另一类是描述数据离散程度的，如极差、方差、标准差。

一、引入方差

苏科版教材是在学习了第一类描述数据集中程度的平均数、中位数和众数的概念后，根据情况需要考虑数据的离散情况。如A组数据：9，10，11，9，12，9；B 组数据：7，10，8，10，12，13。这两组数据的离散程度大小怎样比较？学生可以根据数据绘制图直观感知数据B 比较散，也可以发现散是相对于前面学习过的描述数据集中程度的平均数。因为平均数是数据最集中的反映，“散”与“不散”是相对这个集中作比较的；若以0 分作比较对象，两组数据对0 来说都较“散”了，则很难作判断。

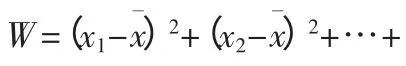
在教学过程中，教师要让学生感受到：为什么要引入方差概念，也就是是数学知识继续发展的必要性；怎样引入方差，涉及具体解决方法；在引入方差过程中为什么要与平均数作差，为什么对差作平方，又为什么对平方后的和要除以n 等等，弄清了这些问题，概念的来龙去脉就清晰了，同时不断让学生面临问题，寻找解决问题的方法，不断完善方法，解决问题。

二、方差概念的理解

1.方差单位的理解

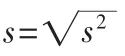
2.方差与极差的区别

极差是一批数据中最大值与最小值的差，简洁明了地描述了这批数据的波动范围。说明了极差也能反映一批数据的离散程度或波动大小。但是很粗糙。因为极差仅反映这批数据中两个极端值的离散度，并不能准确反映这批数据离散的整体情况。而“方差”充分利用每个数据的作用，削弱极端数据的作用，整体反映这批数据的离散程度。

3.比较离散程度与平均数的关系

在教学过程中发现教材中的习题的两组数据的平均数都是相同的。在平均数不等的时候是否可以比较数据的离散程度？这是学生学习的一个疑问。其实每批数据的离散程度都是相对这批数据的平均数的，所以平均数不一定要相同。在实际应用中，当两批数据的平均数差异较大时，先考虑平均数的作用。当两批数据平均数相等或很接近时，用方差来刻画其离散度，根据离散度来进行选择。

“方差”是中学数学中的一个概念，注重概念的本源，每一个概念的产生都有其丰富的知识背景，舍弃这些背景直接抛给学生会让学生感到迷茫。数学概念是随着数学知识的发展而不断发展的，“学习最好的途径是自己去发现”，这需要我们教师理解数学概念，并能创设情境让学生经历一遍发现与创新的过程，这样学生在获得概念的同时也培养了创新精神。