福建省2015年三角函数解法探究

吴明庭

（福建石狮石光中学）

三角函数历来都是高中数学的重要组成部分，是高考中的重点和难点，同时也是必考内容，三角函数在考试中的比重和分值较大。函数的求值问题实质就是三角转换的基础内容，通常包括三种类型：非特殊三角函数式求值、解三角形求值以及位置角的三角函数式求值。对于这类问题的解答，需要熟练掌握三角函数的基本公式以及变换形式，与此同时，还会运用到相应的技巧与方法，才可以简洁、迅速又准确地对式子化简求值。2015 年福建省高考试卷中就包含典型的三角函数试题，本文摘取了其中的试题，通过这几道题的解法，来探究和感悟三角函数的求值方法。

一、考试原题：2015 年高考福建卷理科第II 卷，第19 题

已知函数f（x）的图像是由函数g（x）=cosx 的图像经如下变换得到：先将g（x）图像上所有点的纵坐标伸长到原来的2 倍（横坐标不变），再将所得到的图像向右平移个单位长度.

（Ⅰ）求函数f（x）的解析式，并求其图像的对称轴方程；

（Ⅱ）已知关于x 的方程f（x）+g（x）=m 在［0，2p）内有两个不同的解a，b.

（1）求实数m 的取值范围。

（一）点评

此题主要通过考查学生对三角函数中图像与性质、三角恒等式转换等基础知识，重点测试了学生综合解题能力，包括运算求解能力、抽象概括能力、推理论证能力等多种能力，同时还考查了学生函数与方程思想、分类与整体思想、转化与规划思想、数形结合运用能力等多种综合学习能力及思想。

（二）试题解析

（Ⅰ）纵向伸缩或平移：g（x）→kg（x）或g（x）→g（x）+k；

横向伸缩或平移：g（x）→g（ωx）（纵坐标不变，横坐标变为原来的倍），g（x）→g（x+a）（a＞0 时，向左平移a 个单位；a＜0 时，向右平移a 个单位）；

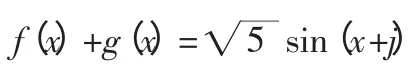
解法一：

（Ⅰ）将g（x）=cosx 图像上所有点y 轴坐标伸长到原来的2倍，x 轴坐标不变；

于是，得到y=2cosx 图像，然后将y=2cosx 的图像向右平移个单位长度；

（1）（fx）+g（x）=2sinx+cosx

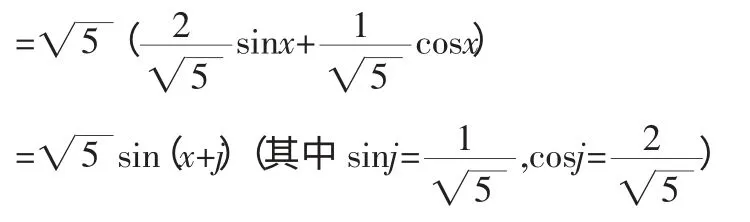
解法二：

（1）参照解法一

（2）①参照解法一

所以cos（a+j）=-cos（b+j）

于是：

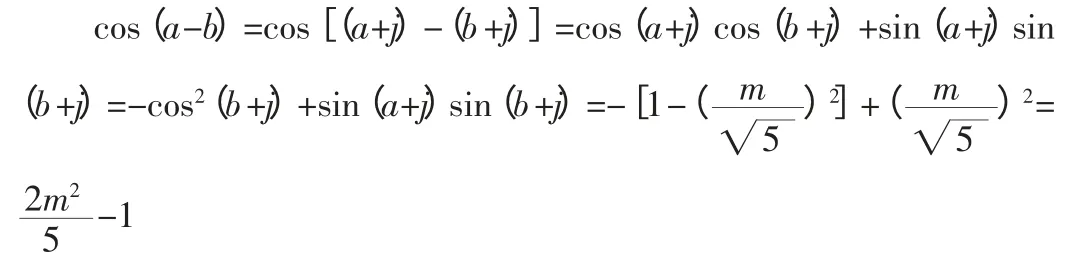
此方法重点考查的是三角函数图象性质及其变化公式，同时考查了辅助角公式以及诱导公式。通过证明对比，不难看出，福建高考数学试题具有明显的开放性，问题的答案也不是唯一的，解答此题需要具备统筹思想，将想象、联想、分析、类比、整合以及推理有效地应用到解题过程汇总，以此锻炼学生的思维探究能力，因此具有很高的价值，值得以后模拟训练及探究性学习。

二、考试原题：2015 年高考福建卷文科第I 卷，第21 题

（Ⅰ）求函数f（x）的最小正周期；

（1）求函数g（x）的解析式；

（2）证明：存在无穷多个互不相同的正整数x0，使得g（x0）＞0.

（一）点评

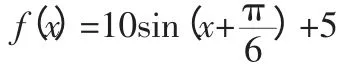
想要证明存在无穷多个互不相同的正整数x0，使得g（x0）＞0，可解不等式g（x0）＞0，只需解集的长度＞1，此时解集中一定含有整数，由周期性可得，一定存在无穷多个、且互不相同的正整数x0.

（二）试题解析

所以g（x）=10sinx-8.

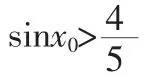
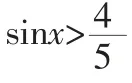
三角函数主要考查的是三角函数的单调性、周期性、奇偶性以及最值问题，同时还结合三角函数的图像、三角恒等变换、函数模型的应用、正余弦定理及其应用以及平面向量及其应用。结合以上考试中的常见问题，可以回顾以往高考试卷中关于三角函数的相关试题。

三、问题回顾

例1.若x 是三角形的最小内角，则函数y=sinx+cosx+sinxcosx的最大值是 （ ）

分析：三角函数的最值问题是三角函数常见的考查内容之一，主要是利用正余弦定理的有界性，通过换元或是其他方法的三角恒等变换来转化问题。本题中三角形的最小内角是不大于的，而（sinx+cosx）2=1+2sinxcosx，可通过换元解决.

点评：涉及sinx±cosx 与sinxcosx 的问题时，通常用换元解决.

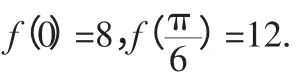
（1）求实数a，b 的值；（2）求函数f（x）的最大值及取得最大值时x 的值.

分析：利用待定系数求a，b，可以利用倍角公式和降幂公式进行问题的转化.

解析：函数f（x）可化为f（x）=asin2x+bcos2x+b.

综上所述，三角函数问题是高考中的常见问题，在解题过程中会运用多种相关知识，这些问题综合性强，方法灵活多样，并且问题本身并不是割裂和独立的，而是相互联系和依存的，通过不同的解题方法，动态地、辩证地看待解决问题，充分利用和调动相关知识，在熟练掌握公式的基础上，融入一些数学思想，辅以一些解题技巧，运用综合分析，尝试从多角度解答问题，拓展思路，发散思维，不断积累经验，关键时刻问题就能迎刃而解。由此可见，对2015 年福建省高考试卷中的三角函数进行剖析和探究，可以集思广益、举一反三，触类旁通，同时引导学生加强合作交流，积极探索并分享经验，可以提高学生的学习效率，为以后的学习和考试打下坚实的基础。