轮式差动转向无人车运动跟踪控制的研究*

熊 璐，黄少帅，陈远龙，杨光兴，章仁燮

(1.同济大学汽车学院，上海 201804； 2.同济大学新能源汽车工程中心，上海 201804；3.中国嘉陵工业股份有限公司(集团)，重庆 401332)



2015190

轮式差动转向无人车运动跟踪控制的研究*

熊 璐1,2，黄少帅1,2，陈远龙1,2，杨光兴3，章仁燮1,2

(1.同济大学汽车学院，上海 201804； 2.同济大学新能源汽车工程中心，上海 201804；3.中国嘉陵工业股份有限公司(集团)，重庆 401332)

在分析车辆传动系统结构特点的基础上，基于差动转向原理，将无人车的运动跟踪控制分为：基于左右轮平均轮速的直线行驶控制和基于左右轮轮速差的行车转向控制。同时，基于抗积分饱和的比例积分控制法，提出了直线行驶下的车速跟踪控制算法；基于状态反馈法，提出了行车转向下的横摆角速度跟踪控制算法。最后，通过实车试验对提出的运动跟踪控制算法进行验证，实现了目标车的遥控行驶。

无人车；差动转向；运动跟踪控制；实车试验

前言

随着社会的进步和科技的发展，无人车已成为汽车发展的一个新趋势。无人车是指不依靠驾驶员操作，通过车载传感器和计算机系统控制，实现安全可靠行驶的车辆。无人车系统是一个综合性的系统，包括许多子系统和相关技术，如环境感知、规划决策、定位导航、运动控制和控制体系等[1-3]。其中，运动控制作为无人车控制系统中的底层实现部分，其性能的好坏直接影响到无人车的自主行驶。

自从履带差动转向理论应用到轮式车辆以来[4]，由于轮式差动转向车辆具有结构简单及快速、灵活的全地形适应能力，受到了国内外学者的广泛研究。文献[5]中基于魔术公式，建立了六轮差动转向车辆动力学模型，并与阿卡曼转向原理的车辆进行了详细对比；文献[6]中对六轮独立驱动差动转向车辆进行了研究，采用分层式的控制结构，通过控制车辆轮胎力来实现车辆的运动跟踪控制；文献[7]中设计了一种基于反馈线性化的跟踪控制器来完成车辆的运动跟踪控制；文献[8]中使用滑模变结构方法设计了一种运动跟踪控制器，并给出了该方法基于Lyapunov稳定性的分析；文献[9]中设计了两个滑模控制器对车辆的直线行驶和转向运动分别进行控制，有效地补偿了轮胎与地面间建模的不准确性。

显然，现阶段对于无人车运动跟踪控制的研究方法较多，但大部分都是基于理论仿真，没有经过实车的验证。本文中从工程实践的角度出发，在分析传动系统结构特点的基础上，基于差动转向原理，利用抗积分饱和的比例积分控制法和状态反馈法设计了轮式差动转向无人车的运动跟踪控制算法，并在实车试验中验证了所设计的算法。

1 传动系统结构特点

图1为无人车动力传动系统简图。该无人车底盘由某轻型8×8全地形车改装而成，其底盘动力传动系统由前传动箱、自动变速器、闭式液压差速转向系统、综合传动箱和轮边减速机构等部件组成。

图2为差动转向原理图。车辆由内燃机的双功率流来驱动，其中转向通过闭式液压回路(变量泵和定量液压马达)差速转向系统实现：发动机动力经前传动箱后分为两路，其中，直驶流通过自动变速器，传到综合传动箱内的行星机构的外齿圈；转向流则通过前传动箱、液压泵和液压马达，传到行星机构的太阳轮，由反向机构实现左右旋转反向；两路动力在综合传动箱处汇流后通过行星架输出。

2 整车动力学模型

为了简化整车动力学模型，假设车辆仅平行于地面运动，忽略车辆的垂向运动、俯仰运动和侧倾运动。

如图3所示，车辆在固结有地面惯性坐标系(Xg,Yg)的二维平面上运动。为方便描述车辆的运动，定义一个车辆坐标系，其原点在车辆质心(COM)。

假设[XYθ]T∈R3表示车辆在大地坐标系中的坐标，其中，X和Y分别表示车辆质心的位置，θ表示车辆的航向角(图中为车辆坐标系和地面惯性系的夹角)。

(1)

根据牛顿第二定律，整车动力学也可由下面的方程来描述：

(2)

(3)

(4)

其中：

(5)

式中：Fxi和Fyi分别为第i个轮胎上的纵向力和侧向力；Mz为各个车轮施加在车身上总的横摆力矩。

3 运动跟踪控制算法设计

由于车辆执行器系统响应速度、控制精度和车载传感器数量的限制，从整车角度对车辆进行控制难度较大。因此，本文将依据车轮轮速对车辆进行控制。然而，其左右两侧传动机构是通过行星机构相互耦合连接的，不能对每侧车轮独立控制。但连接车轮的行星机构是一个2自由度输入系统(分别对应直线行驶和转向行驶)，故可以将车辆的运动跟踪控制分开进行：基于左右轮平均轮速进行直线行驶控制和基于左右轮轮速差进行转向行驶控制。运动跟踪控制架构如图4所示，主要包括参考信号计算、车速控制和转向控制3大部分。

3.1 参考信号计算

3.3.1 行车需求参考信号

上层规划决策系统发出3个行车需求参考指令：参考车速、参考转向曲率和参考横摆角速度。其中，参考转向曲率用于正常行车转向，而参考横摆角速度用于原地转向(pivot steering, PS)。通过式(6)，将这些指令统一为参考车速指令vc和参考横摆角速度指令γc：

(6)

将上层指令统一后，有必要对其进行信号限制和信号滤波，如图4所示。

其中，参考车速信号为

(7)

式中：vmax和vmin分别为设计最大车速和最小车速(也即倒车最大车速)，m/s；τv为滤波时间常数，τv=0.4。

参考横摆角速度信号为

(8)

式中：aymax为最大侧向加速度，aymax=0.8μg，m/s2，μ为路面附着系数；τγ为参考横摆角速度信号滤波的时间常数，考虑到闭式液压差速转向系统的响应速度相对直驶系统慢，为保证两系统的响应带宽接近，取τγ=0.25。

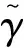
(9)

式中：Kγ和kγ均为正常数；θγ为PI控制器的作用范围指标；sat(·)为饱和函数。显然，当控制器未饱和时，系统以比例系数为kP=Kγkγ和积分系数为kI=kγ的比例积分控制器对误差进行修正；当控制器饱和时，则以最大值定值来进行修正。

3.1.2 参考轮速信号

在如图3所示的坐标系中，根据车辆运动与车轮转速之间的关系可得到参考轮速信号为

(10)

式中：ωl_ref和ωr_ref分别为左右侧车轮的参考角速度，rad/s；vref和γref为经过修正过的参考行车需求指令，即参考车速和参考横摆角速度，m/s和rad/s；dl和dr分别为车辆质心到左右侧车轮的距离，m；R为车轮的滚动半径，m。

3.1.3 执行器参考信号

根据基本控制理论，要想让车辆实现运动跟踪控制，须计算相应执行器的驱制动力矩，保证执行器的实际“速度”能够跟踪参考“速度”。研究车辆的执行器系统由发动机、闭式机械液压差速转向装置及制动器构成。其中，发动机为动力源，其输出转速间接反映了车速，所以通过左右轮的平均轮速来描述发动机的输出转速；而闭式机械液压差速转向装置用来实现车辆的转向，其液压马达的输出转速同样间接反映了车辆的横摆角速度，所以通过左右轮的轮速差来描述这一输出转速。

在参考轮速已知的情况下，通过车辆传动系统的传动关系，可以计算出发动机和液压马达的参考速度，如式(11)所示：

(11)

式中：ωeref和ωmref分别为发动机和液压马达的参考角速度，rad/s；α为行星机构特性参数；iws为轮边减速器的传动比；ig为变速器的传动比；ihc为液力变矩器的速比i的倒数，定义为等效速比；im为液压马达输出端减速比。

3.2 车速跟踪控制算法设计

由上文可知，对车速的控制将被转化为对发动机输出转速的控制。

3.2.1 控制算法原理

(1)控制问题描述及控制率设计

考虑标量非线性系统：

(12)

式中：x为系统的状态；f(x)连续，且满足局部Lipschitz条件[10]；u为系统的控制输入；y为系统的受控输出。

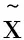
(13)

对式(13)误差约定设计镇定控制律：

(14)

其中：Ku，ku和θu均为正常数，且满足：

(15)

式中非负数Lf为系统函数f的Lipschitz常数。

(2)控制算法稳定性分析

本文设计的式(14)控制律为一带抗饱和策略的比例积分控制，控制器在未饱和时只是一个比例积分控制。然而，由于系统参数变化、外界干扰及建模不精确等因素都会对系统镇定的稳定性产生影响，长时间无法镇定可能会使积分项不断增大，从而导致执行器过早饱和，损害系统的瞬态响应甚至是稳定性；抗饱和策略能够保证在执行器饱和以后仍可使系统镇定收敛。

(a)当|s|≥θu时，所设计的控制器参数只要满足一定条件，就能保证|s|在有限时间内收敛到(0,θu)范围内，且此后都在该范围内。

记Ms为误差与误差积分流形，即

|ε(t0)|≤θu/ku}

(16)

其几何意义如图5中的阴影部分所示。

误差积分的集合Me为

Me={ε||ε≤θu/ku|}

(17)

则由式(15)可知，只要ε(t0)≤θu/ku，对任意t>t0，恒有

|ε(t)|≤θu/ku

(18)

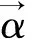
在线段AB以上，s向流形Ms运动，只要满足式(19)即可。

(19)

对式(19)展开，得

(20)

因此，结合式(19)，Ku需满足条件：

(21)

在线段CD以下，s向流形Ms运动，同理，只要Ku满足条件：

(22)

综合条件式(21)和式(22)可得

(23)

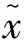
将式(14)代入式(13)，则误差系统可被转化为

(24)

显然，只要系统能够满足式(25)，则系统一定是渐近稳定的。

(25)

由于系统函数f连续，且满足Lipschitz常数为Lf的局部Lipschitz条件，因此式(25)进一步被明确为

(26)

3.2.2 车速跟踪控制算法

依据前文算法原理，设计车速跟踪控制的控制律，并给出算法稳定条件。

根据车辆系统动力学和动力传动关系，受控系统的状态方程为

(27)

式中：Je为发动机及其附属部件的等效转动惯量，kg·m2；ωe为发动机的实际角速度，rad/s；R为车轮的滚动半径，m；Fx为轮胎力函数，N；κ为动力传动系统的传动函数，与系统的状态变量无关；RFxκ为发动机的所有负载，包括直驶流负载Mdl、转向流负载Msl和风扇散热负载Mfl，N·m；T为系统的控制输入，也即发动机的输出转矩，N·m。

设计一个可靠实用的控制律，使发动机输出转速能够稳定地跟踪由参考信号计算模块得到发动机的参考角速度ωeref。

(28)

同理，根据上面的理论分析，可以设计一个稳定的控制律：

(29)

式中：KT,kT和θT均为正常数，在实车标定测试中标定，它们满足以下条件：

(30)

式中：Fz为轮胎的垂向载荷，N；μ为估计的最大路面附着系数；非负数Lp为系统负载函数-RFxκ的Lipschitz常数。

3.3 横摆角速度跟踪控制算法

为使车速跟踪和横摆角速度跟踪能够协调一致，在横摆角速度跟踪控制中，发动机转速以车速跟踪控制中的参考转速为准，不作为横摆角速度跟踪控制中的控制输入，仅视为控制系统的参数。这样，横摆角速度跟踪控制系统将成为一个单输入(变量液压泵斜盘开度)-单输出(定量液压马达转速)系统。鉴于车辆转向执行器的特点，参考横摆角速度信号被转化为参考液压马达转速信号，并由参考信号计算模块给出。

受控对象变量液压泵-定量液压马达组成的闭式回路系统，其动力学数学模型为

(31)

式中：Jm为液压马达及其附属部件的等效转动惯量，kg·m2；ωm为液压马达的实际角速度，r/min；ξ为黏性阻尼系数；Msl(ωm)为转向流负载，N·m；qm为定量液压马达的排量，L/r；ηmm为系统机械效率；p为高压管路的压力，MPa；V0为液压管路容积，L；E为液压油弹性模量，MPa；ηmv为液压马达的容积效率；qbmax为变量泵的最大排量，L/r；ηbv为液压泵的容积效率；nb为液压泵的转速，r/min；k为液压泵的斜盘开度，%。

其中，转向流负载Msl同样可以表达成轮胎力的形式：

(32)

整理系统，令

a12=500qmηmm/Jm/π

a21=-30Eqm/π/ηmv/V0

a22=0；b1=0；b2=Eqbmaxηbv/V0，u=nbk

将式(31)转换成状态方程的形式：

(33)

令|λI-A|=0，可得系统矩阵A的特征值为

(34)

由现代控制理论[11]可知，只要系统矩阵的所有特征值为负，则该系统一定是稳定的。因此，根据式(34)特征值表达式，式(33)系统的稳定性主要由a11的正负来决定。

考虑到目标车使用的轮胎类型及数量，与商用车类似。因此，根据文献[12]，可以假设轮胎力与滑移率单调递增，则a11一定为负，即式(33)系统是稳定的。此外，即便这样的假设不成立，一样可以通过线性误差系统的状态反馈来保证稳定液压马达角速度控制收敛。

因此，对于给定参考输出信号为y=ωmref的跟踪控制系统，始终有控制输入为

(35)

的控制律使式(33)系统输出参考信号的跟踪渐近稳定。

4 实车验证

采用汽车嵌入式系统开发V模式，针对选用的整车控制器，应用基于模型的设计方法，利用Matlab/Simulink工具对算法建模，并在仿真测试、软件在环测试和硬件在环测试通过的基础上，在如图6所示的目标车上进行实车测试。

由于对差动转向车辆性能的试验和评价尚未有相关的标准法规，本文中根据项目需求和实际条件设计了以下的试验工况：直线加、减速工况用来验证车速跟踪控制效果；原地转向工况用来验证横摆角速度跟踪控制效果；最后，参考国标GB/T6323.1—94[13]的蛇行试验规范，采用人为闭环遥控的工况来验证运动跟踪控制的整体控制效果。试验中，目标指令都通过遥控装置给出。

4.1 直线加、减速试验工况

直线加、减速试验设定的目标车速为10，16和12km/h，通过比较目标车速和实际车速、参考发动机转速和实际发动机转速来验证车速跟踪的控制效果。试验结果如图7和图8所示。

由图可见，车速能够快速准确地实现跟踪。需要注意的是，图8中的发动机参考转速较高，出现了大的类似超调的现象，这是因为自动变速器中液力变矩器的泵轮和涡轮的速比在车辆起步时比较大，随着车辆起步，该速比逐渐变小，发动机参考转速也趋于正常。

4.2 原地转向试验工况

原地转向试验是在空挡下进行的，操作者通过遥控装置给出参考横摆角速度值，并尽量在该数值上保持一段时间不变，然后切换下一个不同的数值，来验证横摆角速度跟踪的控制效果。试验结果如图9和图10所示。

由试验结果可以看出，横摆角速度能够实现稳定跟踪。但由于试验车辆的自动变速器不稳定，在试验后半程中(15 s以后)挡位跳到1挡，车辆出现小的前进速度，因此试验中断。

4.3 蛇行试验工况

在做蛇行试验之前，考虑到操作者的遥控水平有限，自动变速器固定在1挡，并以20km/h的入弯速度进行试验，试验中为尽量保持初始车速恒定，将参考车速设为标定量并在试验前给定，而操作者通过遥控装置只进行转向控制。蛇行工况的试验结果如图11～图14所示。

从图11和图12中可以看出，车速能够保持稳定，说明车速跟踪控制能够使车速在转向中依然保持稳定；从图13和图14中可以看出，横摆角速度跟踪控制能够实现车辆横摆角速度的稳定跟踪。

5 结论

针对目标车，分析了其传动系统的结构特点，在此基础上，基于差动转向原理，提出了其实现运动跟踪控制的可行性方法，即将车辆运动跟踪分为基于左右轮平均轮速的直线行驶控制和基于左右轮轮速差的行车转向控制。为了顺利实施上述运动跟踪方法，基于抗积分饱和的比例积分控制法，设计了直线行驶下的车速跟踪控制算法；基于状态反馈法，设计了行车转向下的横摆角速度跟踪控制算法。最后，通过设计相应的试验工况，在实车试验中验证了所设计的算法，能够满足上层的稳定跟踪要求。但是由于试验条件和目标车本身的限制，算法并没有在高速情况下得到验证，这将是以后工作的方向。

[1] Morita T, Takahashi H, Satonobu J, et al. An Approach to the Intelligent Vehicle[C]. Intelligent VehiclesSymposium, 1993: 426-431.

[2] 支高英. 智能车辆视觉导航算法的研究[D]. 天津:天津工业大学, 2009.

[3] 黄岩, 吴军, 刘春明, 等. 自主车辆发展概况及关键技术[J]. 兵工自动化, 2010(11):8-12.

[4] Weiss K R.Skid-steering[J]. Automobile Engineer, 1971, 61(4):22-25.

[5] Li X, Zhang Y, Hu J, et al. Lateral Dynamic Simulation of Skid Steered Wheeled Vehicle[C]. Intelligent Vehicles Symposium (IV), IEEE, 2013: 1095-1100.

[6] Kang J, Kim W, Lee J, et al. Skid Steering-Based Control of a Robotic Vehicle with Six In-Wheel Drives[J]. Proceedings of the Institution of Mechanical Engineers Part D Journal of Automobile Engineering,2010, 1:1-23.

[7] Caracciolo L, De Luca A, Iannitti S. Trajectory Tracking Control of a Four-wheel Differentially Driven Mobile Robot[C]. Proceedings - IEEE International Conference on Robotics and Automation,1999:2632-2638.

[8] Yi J, Song D, Zhang J, et al. Adaptive Trajectory Tracking Control of Skid-steered Mobile Robots[C]. Proceedings - IEEE International Conference on Robotics and Automation, 2007: 2605-2610.

[9] Lucet E, Grand C, Sallé D, et al. Dynamic Sliding Mode Control of a Four-Wheel Skid-Steering Vehicle in Presence of Sliding[C]. 17th CISM-IFToMM Symposium on Robot Design, Dynamics, and Control, 2008.

[10] Hassan K Khalil. Nonlinear Systems (3rd Edition)[M]. 北京:电子工业出版社, 2007.

[11] 王新生, 曲延滨. 现代控制理论基础[M].哈尔滨: 哈尔滨工业大学出版社, 2009.

[12] Pauwelussen J P. The Single Track Vehicle Matel[J/OL]. https://www.tut.fi/ms/muo/tyreschool/moduulit/moduuli_10/hypertext/5/5_1.html,1999.

[13] GB/T 6323.1—94 汽车操纵稳定性试验方法—蛇行试验[S].1994.

A Research on Motion Tracking Control for Unmanned Ground Vehicle with Wheeled Skid-steering

Xiong Lu1,2, Huang Shaoshuai1,2, Chen Yuanlong1,2,Yang Guangxing3& Zhang Renxie1,2

1.SchoolofAutomotiveStudies,TongjiUniversity,Shanghai201804; 2.CleanEnergyAutomotiveEngineeringCenter,TongjiUniversity,Shanghai201804;3.ChinaJialingIndustrialCo.,Ltd. (Group),Chongqing401332

With an analysis on the structural features of vehicle transmission system, and based on the principle of skid-steering, the motion tracking control for unmanned ground vehicle is divided into straight-line driving control based on the average rotation speed of left and right wheels and cornering control based on the rotation-speed difference of left and right wheels. Meanwhile, a vehicle speed tracking algorithm is proposed for straight-line driving based on PI control with integral anti-windup, and a yaw rate tracking algorithm is proposed for cornering based on state variable feedback. Finally, the motion tracking algorithms proposed are verified by real vehicle tests, realizing the remote control driving of target vehicle.

unmanned ground vehicle; skid-steering; motion tracking control; real vehicle tests

*国家自然科学基金(51475333)资助。

原稿收到日期为2015年7月2日，修改稿收到日期为2015年7月31日。