解析函数的物理意义及其应用
瑛 瑛
(呼伦贝尔学院 数学统计学院,内蒙古 海拉尔 021008)
解析函数是复变函数论研究的主要对象,因此,复变函数论又称为解析函数论.解析函数不仅具有多种性质,也有着广泛的应用.但很多教材中,尤其物理、电信等专业的《复变函数与积分变换》教材中很少涉及到解析函数的物理意义及应用.本文简明地介绍了解析函数的物理意义,并例举了典型的应用例子,从而使解析函数的概念从抽象到具体,更容易让学生理解.
1 复变函数的物理意义
物理学上有很多不同的稳定平面场,所谓场就是每点对应有物理量的一个区域,可用一个复变函数表示.
例1 平面向量场的复变函数表示.
分析:如果一个向量场E为平面场,则E上所有的向量都平行与某一个平面S.这样,向量场E就可以用平面S上的向量场来表示.在平面S上采用向量的复数记法,那么向量场E就唯一地确定一个复变函数

这里,Ex,Ey分别表示向量场E在x轴和y轴上的两个分量.反之,已知某一个复变函数w=u(x,y)+iv(x,y),由此也可以作出一个对应的平面向量场
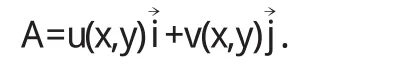
2 解析函数的物理意义
一个无源无旋的平面向量场可用一个解析函数表示,则这个解析函数是该平面向量场的复势函数.
例2 平面静电场用解析函数表示.
分析:选取一个有代表性的平面作为z平面,设D是电场中的一个单连通区域,如果D内每一点电场强度f(z)=u(x,y)+iv(x,y),由场论知识,有
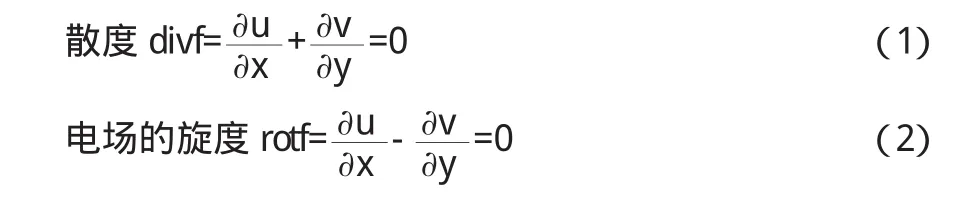
由式(1)可知,-vdx+udy是某一个二元函数ψ(x,y)的全微分,即有

ψ(x,y)称为电场的力函数,其等值线ψ(x,y)=c称为电力线.
由(2)可知,存在函数 φ(x,y),使得
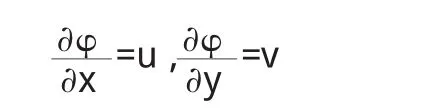
φ(x,y)称为电场的势函数,其等值线φ(x,y)=c称为等势线.
由(2)和(3)得到偏微分方程组
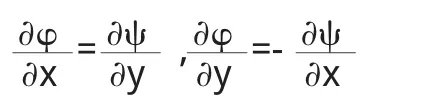
以上方程是C-R方程,因此得到一个解析函数
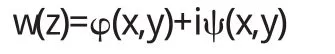
该函数称为静电场的复势函数.显然,f的复势不是唯一确定的,可以相差一个常数.
类似地,对任一既无源又无旋的平面向量场总可以构造一个解析函数,即复势与之对应.流体力学中无旋流动的研究中也经常用到解析函数,利用复势来刻画流动比用复速度方便,因为由复势求复速度只用到求导数,反之则要用积分.另一方面,由复势容易求流线和势线,这样可以了解流动的情况.
例3 已知平面流速场的复势f(z)为(z+i)2,求流动的速度以及流线和等势线方程.

故该流体流动的水平及垂直分速分别为2x,2(y+1).
综上所述,解析函数具有明确的物理意义和广泛的应用背景.在复变函数论的课堂教学中,把解析函数及其他的一些概念和定理等的物理意义及应用作以介绍,对提高学生的学习兴趣及培养他们理论联系实际的能力有很大的帮助.
〔1〕钟玉泉.复变函数论[M].高等教育出版社,2004.
〔2〕华中科技大学数学系,复变函数与积分变换(第三版)[M].高等教育出版社,2008.
〔3〕余家荣.复变函数[M].高等教育出版社,2005.
〔4〕张金锋,等.解析函数在平面静电场中的应用性研究[J].吉林师范大学学报 2013(2):84-86.

