关于一致连续的判定与应用
李江华
(广东理工学院,广东 肇庆 526100)
关于一致连续的判定与应用
李江华
(广东理工学院,广东肇庆526100)
本文以一致连续函数的判定与应用为研究对象,基于现有判定定理,分析函数一致连续的性质,增强一致连续的应用.
函数思想;函数方程式;一致连续;判定定理
1 引言
函数是构建中学数学的主旋律.而函数思想在高中数学的运用较多.它起到承上启下的作用.在考虑到相关运动变化、相依关系的同时,以一类状态过渡至研究变化的过程,从而确立相关的思想方式.在高中数学的范畴,关于不等式的研究,如何才能体现相应的函数思想,培养学生应用函数解决不等式的问题,进一步挖掘培养学生的思维深刻性.为此,我们必须从问题分析开始,对函数思想加以论述,并详细地探究.
2 函数的基本概念
2.1函数概念
对于函数的概念,我们可定义为,在一个变化的过程,设定两个变量,分别为x、y,对于x,均有唯一值y与之对应,即x为自变量,y是x的函数,而自变量x取值的集合,与x相应的y称为函数值域.从x→y,在相应的值域均有唯一的f(x)与它对应.它揭示的是定义域、值域与对应法则的关系.
2.2函数思想
运用函数思想,从概念入手,就其性质,对问题加以分析,将其转化为解决技巧.从问题开始,研究彼此之间的关系,运用数学语言,将因素转化为数学模式,从而将问题加以解决.基于方程的思想,结合方程组,对其求解,转换对应的关系,实现函数与方程的转化,从而实现方程组因式分解,得出结果.
笛卡尔方程思想是以问题为主,将数学问题转化为结果,因函数与多元方程区别较少.两者基本无差异.它围绕着二元函数,结合因变量与自变量,探究方程组的求解过程.
列方程、解方程和研究方程的特性,均是通过方程思想加以考虑的.函数方程确定的是数量之间的关系,而函数思想则通过问题的研究,体现着数学特征.函数模型的构建,研究相关的关系.按函数性质,对问题加以分解,结合不同性质,如奇偶性、单调增减、指数函数等.按不同组分的求解,基于显隐条件,构造相关的函数.从问题的现象透视本质,构建彼此之间的关联,构造相应的函数方程.经过变量之间的分析,确定对应的组分,从而研究不同函数之间的关系,挖掘其中的规律变化.
2.3一致连续函数性质
结合数学分析,函数一致连续性是重要的教学内容.它强调的是函数的连续性,基于区间的考虑,它表达的是函数在区间I的分布,而函数一致连续问题是连续函数的性质,基于微积分学的研究,函数的应用将较为重要的.
3 函数一致连续的判定与应用
3.1一致连续的定理
假设f(x)在[a,b]连续,那么判定f(x)在[a,b]是一致连续的.如果∀ε>0,∃δ(ε)>0,对于∀x1、x2∈[a,b],则有|x1-x2|<δ,推出|f(x1)-f(x2)|<ε.那么,函数f(x)在闭区间[a,b]是一致连续的.基于一致连续判定,划分为不同的定理.如下所示:
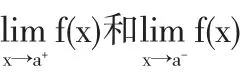
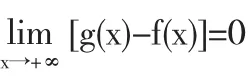
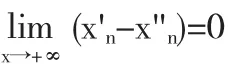
3.2一致连续函数判定
基于3.1定理判断,判定一致连续函数的有效性.因区域连续且为有界函数,它在区域I是一致连续的.基于有限值的判断,结合函数的性质,判定其是否是一致连续的.因函数有界,且区间
例1设f(x),g(x)均在区域I内一致连续且有界,证明:F(x)=f(x)g(x)也于I一致连续.
证明f(x),g(x)有界,为此,M>0,使|f(x)|<M,|g(x)|<M,∀x∈I.判定f(x),g(x)均为一致连续的.
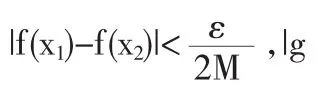

为此,F(x)在区间I内是连续函数,且它们是较为一致的.
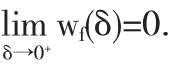
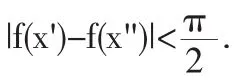
所以,当
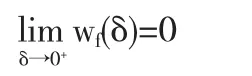
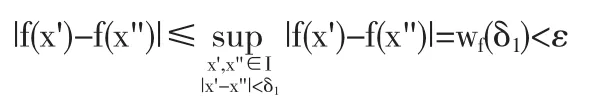
为此,f(x)在I是连续函数,且数值维持一致.
3.3一致连续函数的应用
例1设函数f(x)在[a.b]上连续,且为单调增加函数,a<0<b,证明:
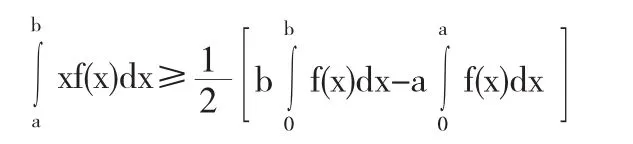
证明令

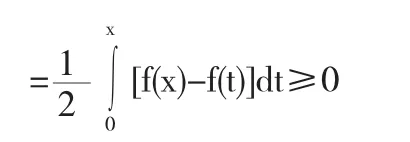
因f(x)为递增的函数,为此,当b>a时,有F(b)F(a)=0,
例2设f(x),g(x)在[a,b]上连续,且满足
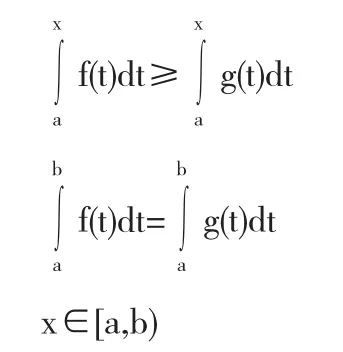
证通过题目设定的条件,我们可以知道,以下简要的分析:
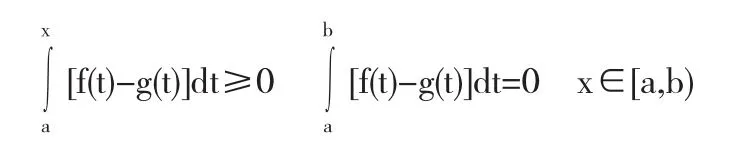
由题设可知,G(x)≥0,x∈[a,b],G(a)=G(b)=0,G'(x)=F(x),从而我们能够确定如下过程:


〔1〕杜家祥.函数在无穷区间上一致连续性的判定[J].宿州教育学院学报,2011(1):91-92.
〔2〕胡适耕,张显文.数学分析原理与方法[M].北京:科学出版社,2008.
〔3〕杨传林.数学分析解题思想与方法[M].浙江:浙江大学出版社,2008.
O172.1
A
1673-260X(2015)11-0001-02

