让个性化教学绽放光彩

福建上杭县临城中心小学（364200） 吴茂生

《义务教育数学课程标准（2011版）》明确指出：“要面向全体学生，适应学生个性发展的需要，使得人人都能获得良好的教育，不同的人在数学上得到不同的发展。”“学生学习应当是一个生动活泼的、主动的和富有个性的过程。”让学生个性得到充分的发展，是一切教育教学改革的终极目标。个性化教学以学生为主体，以“发展个性，培养创新精神”为思想精髓，鼓励学生独立思考、标新立异，以逐步形成独特的思想意识，提高数学素养。数学教学要重视学生个性的存在和发展，以学生的个性差异为依据，运用个性化的教学方法和策略，把学习活动变成自我探究、自我体验的活动，让个性化教学绽放光彩。

一、在活动中体验，培养学生个性

体验是个性化的行为，具有鲜明的个体特点，成功的体验对于学生良好个性的培养有着巨大的推动作用。在教学中要为学生提供广阔的活动空间，让他们以适合自己的认知方式投入到操作活动中去，让他们在自主学习中获得成功的情感体验，从而使他们的创造潜能得到最大限度的发挥。如教学“三角形的面积”时，（1）猜想。怎样算出红领巾的面积？能不能把三角形也转化成学过的图形面积？（2）拼摆。将两个完全一样的直角三角形进行拼摆，看能拼出哪些图形。（3）思考。直角三角形面积与平行四边形面积有什么内在联系？（4）拼摆。两个完全一样的锐角三角形进行拼摆，看能拼出学过的哪些图形。（5）思考。①拼成的平行四边形的底、高分别与锐角三角形的底、高有什么关系？②锐角三角形的面积与拼出的平行四边形面积有什么联系？（6）拼摆。将两个完全一样的钝角三角形进行拼摆，看能拼成学过的哪些图形。（7）思考。①拼成的平行四边形的底、高分别与钝角三角形的底、高有什么关系？②钝角三角形的面积与拼成的平行四边形面积有什么关系？（8）归纳。三角形的面积＝平行四边形的面积÷2＝底×高÷2。（9）多媒体展示下图。很早以前，我们的祖先就已经发现割补法，先作底边上的高和中位线，沿高的一半旋转180°就可拼成一个平行四边形。

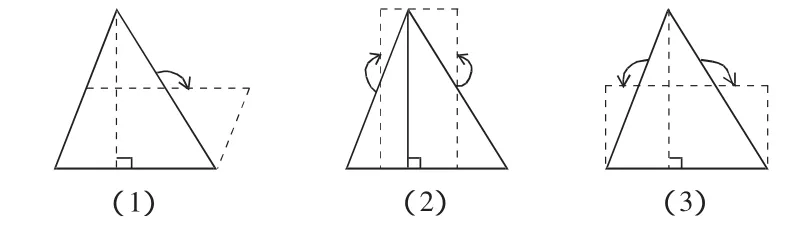
这样教学，学生在动手操作、动脑思考、动眼观察、动口表达的活动中经历和体验了三角形面积公式推导过程，逐步建立清晰而深刻的表象，体现了学生的自主性，使不同层次的学生在活动中建立三角形面积公式，获得丰富的数学活动经验。

二、在探究中创新，发挥学生个性

赞可夫认为：“学生的反映是个体能动的反映过程，应该鼓励学生在教师的指导下独立的探索。通过探索，在掌握知识的同时发展能力。”学生因知识水平、经验不一，兴趣爱好不同，对同一事物的观察方法与角度不同，个性表现也不同。教学中必须尊重学生的个性差异，鼓励学生用自己独特的方式，表示具体情境中的数、数量关系或变化规律，让学生经历“具体事物——个性化表示——数学化表示”的过程，使学习过程成为学生展示个性、表现个性、发挥个性的过程。如“乘法分配律”的教学中，可引导学生对下面问题进行探究。

1.口算并给算式分类。

（2＋10）×4 9×7＋11×7 （2＋8）×5 2×4＋10×4

2×5＋8×5 （12＋18）×5 （9＋11）×7

2.分类整合。有括号的一类，没有括号的一类。

（2＋10）×4 （2＋8）×5 （9＋11）×7 （12＋18）×5

2×4＋10×4 2×5＋8×5 9×7＋11×7

3.观察思考。上、下算式有什么特点？

4.感知规律。观察等式，你发现了什么？

（2＋10）×4＝2×4＋10×4 （2＋8）×5＝2×5＋8×5

（9＋11）×7＝9×7＋11×7

5.验证规律。照样子写出几个这样的算式验证。

6.表示规律。用自己喜欢的方式表示规律。①文字表示。两个数的和同一个数相乘，可以把两个加数分别同这个数相乘，再把两个积相加，结果不变。②字母表示。（a＋b）c＝ac＋bc。③图形表示。（△＋□）×○＝△×○＋□×○。④汉字表示。爱×（数＋学）＝爱×数＋爱×学。

这样，学生在探究中用文字、字母、图形、汉字代替具体的数据，将乘法分配律用符号表达出来，既是符号思想的具体应用，也是学生数学抽象思维能力的提升。

三、在合作中完善，彰显学生个性

心理学研究表明：一个人在小组内学习，除了可以分享同组人的智慧外，还可以最大限度地发挥个人的聪明才智。小学生的自尊心日益增强，他们喜欢受人尊重，渴望个性地发展自我；不同的学生思考问题的方法、解决问题的策略都有自己固有的特点，这种个性化的方法和策略正是展开教学活动最有价值的数学资源。因此，教师在教学中要适当开展合作学习，把课堂有限的时空变成人人参与、个个思考的无限空间，鼓励学生大胆将自己的思维过程展示出来，同时引导学生在合作中学会尊重和欣赏他人，从而使学生在合作学习中不断完善自我。在合作学习中每个学生都有发言交流的机会，可以学习别人的优点，当某一个学生对问题理解有困难时，可以请求其他同学帮助，以达到共同提高的目的。如教学“三角形的认识”时，让学生合作学习。（1）围一围。从4厘米、5厘米、6厘米、10厘米四根小棒中任取三根围一围，看能否围成三角形。（2）填一填。把围三角形的情况填入下表。（3）议一议。通过实践，你们发现了什么？（4）归纳小结，得出结论：三角形任意两边的和大于第三边。

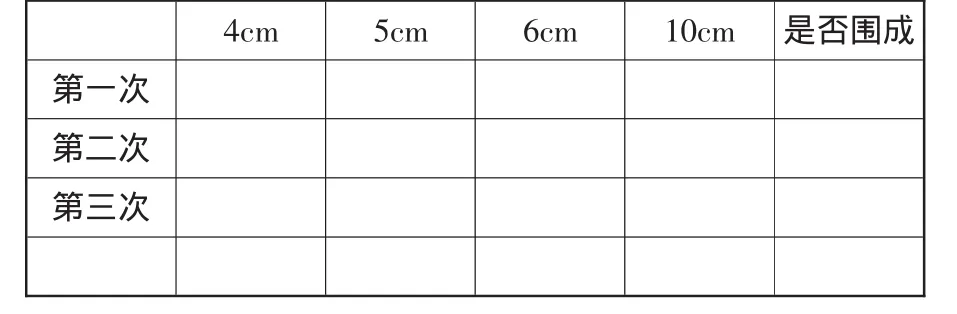
4cm 5cm 6cm 10cm 是否围成第一次第二次第三次

这样合作学习，使学生畅所欲言，满足了学生之间的情感交流，有利于学生自由地发表意见，学生在无拘无束和非强制性的学习中认识了三角形，个性得以充分发展，最终达到互相提高的目的。

四、在质疑中反思，发展学生个性

古人云：“学起于思，思源于疑。”疑是思维的开端，是创造的基础；敢于和善于质疑是学生个性的显著特点，让学生质疑问难是调动学生学习的积极性和主动性的重要手段。发展学生的个性，提高学生的个体素质，既要对有个性的学生持理解、宽容和鼓励的态度，又要鼓励学生质疑问难。教学中教师要引导学生在知识易混处质疑，在课将结束时质疑，在质疑中发展学生个性；同时让学生在体验中学会反思，实现学生与知识的平等对话，最终实现“不仅知其然，而且还知其所以然”，使学生在质疑问难中实现自我超越。如教学“互质数”时，学生容易把“互质数”和“质数”混淆起来，教学中应引导学生质疑：质数和互质数有什么不同，主要区别在哪里？此时，再引导学生通过讨论，明确质数是指一个数，是从一个数约数的个数来定义的，而互质数研究的是两个数之间的关系，是基于两个数的公约数来研究的。又如，教学“十几减9”结束时，我问学生是否还有其他想法，一位学生质疑：15－9，5－9 不够减，我是倒着减的。先用 9－5 得4，再用 10－4 得 6，因此，15－9＝6，这样做可以吗？问题一提出，立刻引来大家议论纷纷，我及时表扬了这位学生，并引导学生讨论、交流，最终达成共识：这种做法是合理的。

这样质疑问难，在比较中解决问题，在反思中深化知识，使学生的情操潜移默化地得到陶冶，个性得到发展。