合理设计“开放题” 培养思维品质

江苏镇江市飞达光彩学校（212312） 杨 军

培养思维品质是发展智力、培养能力的突破口。合理设计和运用一些“开放题”，不仅能有效拓宽学生的思维空间，而且有利于引导学生探索多样化的解题策略，培养学生良好的思维品质。

一、“条件”开放，培养思维的敏捷性

有意识地设计一些有“多余条件”的“开放题”，有利于开放学生的思维方式，灵活选择所需条件，引导学生多角度思考问题，让思维在开放中得以“闪光”，培养思维的敏捷性。

【例1】杨靖把她家6月份家庭支出情况做了整理，有以下一些信息：

（1）全家一共支出3500元，项目大致可分为：伙食、文化娱乐、其他三大类。

（5）文化娱乐比其他支出少用350元。

张老师提出问题：“请选取其中的几个信息，求出文化娱乐的费用是多少元。”

由于题目提供的解题信息比较多，在教学反馈时学生的思路就很宽广。

东东是这样思考的：我选择（1）、（2）、（3）三个条件。根据信息（1）和（2），就可以先求出文化娱乐支出和其他支出的总数。又根据信息（3），就可以求出文化娱乐的支出。

楠楠是这样思考的：我选择（1）、（2）、（4）三个条件。根据信息（1）和（2），就可以先求出伙食支出，又根据信息（4）求出其他支出，最后求出文化娱乐的支出。

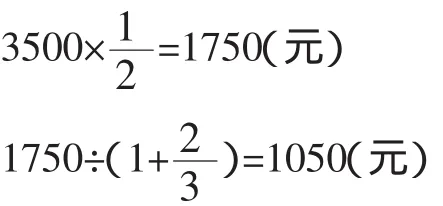
3500－1750－1050=700（元）

帅帅是这样思考的：我选择（1）、（2）、（5）三个条件。根据信息（1）和（2），就可以先求出文化娱乐支出和其他支出的总数，又根据信息（5），就可以求出文化娱乐的支出。

慧慧却是这样思考的：可以选择（1）、（3）、（4）三个条件。根据信息（3）和（4），就可以先求出三个项目的比，又根据信息（1），就可以求出文化娱乐的支出。

把其他支出看成3份，文化娱乐支出是2份，伙食支出是5份，则：

3500÷（3+2+5）=350（元）

350×2=700（元）

可见，不同的条件选择就可以得到不同的解题思路和方法。当然，解法有简便与繁琐之分。可以发现，最简捷的解法应当是第4种。

二、“思路”开放，培养思维的灵活性

不同的思考角度会产生不同的解题方法，体现出不同的思维方式。因此，合理设计一些“一题多解”的“开放题”，有利于引导学生多角度思考，在“多思”中学会“多解”，在“多解”中追求“巧解”，培养思维的灵活性。

【例2】学校组建了田径队，男生人数和女生人数的比是5∶4。已知女生有16人，田径队一共有多少人？

从不同角度思考分析，就会得到不同的解题思路。

思路1：从份数的角度思考，女生的4份是16人，一份是16÷4=4（人），田径队一共是5+4=9份，所以 4×9=36（人）。综合算式是16÷4×（5+4）=36（人）。

思路4：把田径队总人数看作“1”，那么女生人数就是田径队人数，可以直接求出田径队总人数。算式是1

三、“答案”开放，培养思维的深刻性

合理设计一些有“不同答案”的“开放题”，可以引导学生不盲从，不被局部现象所迷惑，有利于引导学生从不同角度去思考问题，做到整体把握，全面分析，三思而后“答”，培养思维的深刻性。

【例3】有一个等腰三角形，其中两个角的度数比是1∶2。顶角的度数是多少？

初读本题，不可盲目解答，而应仔细分析，全面地思考，分多种情况一一考虑。

第一种情况：如果1∶2是底角和顶角的度数比，因为等腰三角形的两个底角相等，所以三个内角的度数比是1∶1∶2。如图 1，三个角的总份数就是 2+1+1=4 份，180÷4=45度，顶角度数：45×2=90度。

图1

图2

第2种情况：如果1∶2是顶角和底角的度数比，因为等腰三角形的两个底角相等，所以三个内角的度数比也可以是1∶2∶2。如图2，三个角的总份数就是1+2+2=5份，180÷5=36度，顶角度数：36×1=36度。

题目中没有告诉我们钢管的长度，所以结果有多种可能。

第一种情况：如果钢管的长度大于1米，假设为2米，那么第一次用去它的，就是米，可见，第1次用去的长度多一些。

第二种情况：如果钢管的长度小于1米，假设为0.8米，那么第一次用去它的，就是=0.24米，可见，第2次用去的长度多一些。

可见，在解“开放题”时，在出现多种情况时，要充分考虑各种情况，学会用分类的思路进行讨论，这非常利于培养学生思维的深刻性。