关注三点，生成课堂精彩

江苏如皋市江安镇江安小学（226534） 严世林

课堂教学是一个充满生成性的、不确定的、动态发展的过程。在这个过程中，学生会有奇思妙想，也会出现诸多错误……教师要时刻关注学生的学习动态，精心预设，合理调控，动态生成，只有这样，才能使课堂教学更加精彩。

一、关注学习起点，主动应对生成

在学习数学新知之前，学生对所学的新知都会有一些或多或少的学习经验，这也是学生学习的起点。在数学教学中，教师要时刻关注学生学习的起点，依据学生的理解接受程度，设计出有效的教学策略，起到对教学过程随时调控的教学目的。

如在教学“时，分，秒”之前，我出示了以下问题：1.钟面上一共有（ ）个大格；2.每个大格内又分为（ ）个小格；3.钟面上一共有（ ）个小格。大多数学生看到题目都有种无从下手的感觉，说明了学生对这种表述方式在理解上还存在一定困难。在准确把握学生起点的基础上，我换了个提问的形式：“你知道这个钟面上一共有多少个数字吗？每个数字之间都有一定距离，我们把个距离称之为一大格，现在，你知道钟面上有多少个大格吗？”基于学生理解提出问题，学生很快就能准确给出答案。

在“时，分，秒”的教学中，认识钟面，了解大格、小格指的是什么，以及分清时针、分针、秒针是教学的基础。在这个教学过程中，教师通过问题准确把握了学生的起点，然后立足于起点，在基于学生理解认识的基础上展开。这样的教学，为课堂教学的动态生成提供了保证。

二、关注学习疑点，充分开发生成

学贵有疑。学生在学习的过程中，只在有疑问时，才会有进一步探索的要求。因此，教师要充分关注学生的学习疑点，巧妙开发利用，进而使学生在存疑、探疑、释疑的过程中加深对问题的认识，生成精彩的课堂。

如在教学“有余数的除法”时，教学重点是让学生在摆一摆、分一分中了解余数以及有余数的除法的含义，并且理解除数与余数之间的关系。在教学时，首先以“把7个苹果平均分给3个学生，每个学生可以分到几个，还余下几个”为例，让学生摆一摆、想一想，学生很容易就得出了“每个学生分2个，还余下1个”的结论。此时，我顺势指出：“余下的这个我们就把它叫做余数。现在你们还有什么疑问吗？”在教师的鼓励和支持下，有学生提出自己对除数和余数之间的关系还不是很了解。于是我让学生分别拿出8根小棒、9根小棒、10根小棒……摆成正方形，并在旁边写上算式。

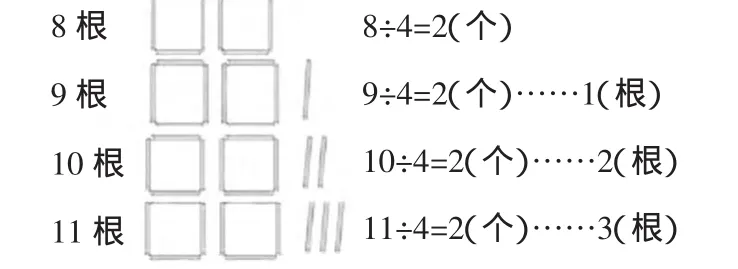
学生经过动手操作得出以上结果后，我再让学生仔细观察这些算式中的除数与余数，经过比较，学生轻松得出了“余数一定比除数小”的结论。

在这个教学过程中，面对学生的疑惑，教师没有直接告知，而是巧妙地开发利用，让学生通过亲自动手实践来解决这个谜团，使得学生的感受更深刻，提高了学习效率。

三、关注易错点，有效促进生成

富兰克林曾说：“垃圾是放错了地方的宝贝。”在数学教学中，面对教师的提问，学生总会出现各种各样的错误。其实，教师如果利用好这种错误，也可以使错误资源绽放精彩。因此，教师面对学生的错误时，不妨借“错”发挥。

如教学“利用商不变的规律进行简便计算”时，我以“8500÷200”为例展开教学，依据被除数和除数同时扩大或者缩小的规律，把原式化为“85÷2”，进而得出了“得数是42，余数是100”的结果。有学生马上提出了反对意见：“你不是常说余数一定要比除数小吗？在这里余数怎么比除数大啊？我故作茫然，借题发挥道：“对呀，余数是不可以比除数大的呀，看来这样的简算有问题！大家再认真思考一下，确定是不是真的计算错了？”学生立即认真查找，发现余数100是相对除数是200时的余数，而不是改变后的除数是2的余数，这样一来，学生豁然开朗。

当学生出现错误时，教师借“错”发挥，引领学生主动探究，发现错误的本质。这样，学生在发现错误、追究本质的过程中，收获了柳暗花明的惊喜，进而把课堂推向了高潮。

总之，在数学教学中，关注学习起点就是关注学生学习的就近发展区；关注学习疑点，就是关注学生探究的起点；关注学习错点，就是真正的以生为本。就让我们时刻关注学生，发现问题，主动应对，打造出充满无限活力的数学课堂吧！