让解题思路自然流淌——浅谈数学解题思维能力的培养

赵建丽

（山东省聊城大学数学科学学院2014 级研究生 东营垦利县中等职业专业学校）

在数学解题中，通常会出现解完题，学生高呼“太巧了”。其实这种现象不正常，会出现这种情况，是因为有些人喜欢故弄玄虚，弄一些技巧性强、方法奇妙的解法，以此显示自己解法的高明。从数学思维的角度看，自然的想法才是学生能够想到的方法，才能引起师生的共鸣。

例如，（全国大纲卷2012 年17 题）已知△ABC的三个内角A，B，C成等差数列，且2b2=3ac，求角A。

解：由题意知2B=A+C，且A+B+C=180°，知∠B=60°，则A+C=120°.

由2b2=3ac及正弦定理知2sin260°=3sinAsinC知sinAsinC=

则cos（A+C）=cosAcosC-sinAsinC=cosAcosC

得cosAcosC=0，则cosA=0或cosC=0。

若cosA=0，则A=90°；

若cosC=0，则C=90°，从而A=180°-90°-60°=30°。

所以∠A=90°或∠A=30°

通法一、化角的关系为边的关系，运用方程思想和余弦定理求A。

解：由题意知2B=A+C，且A+B+C=180°，知∠B=60°，

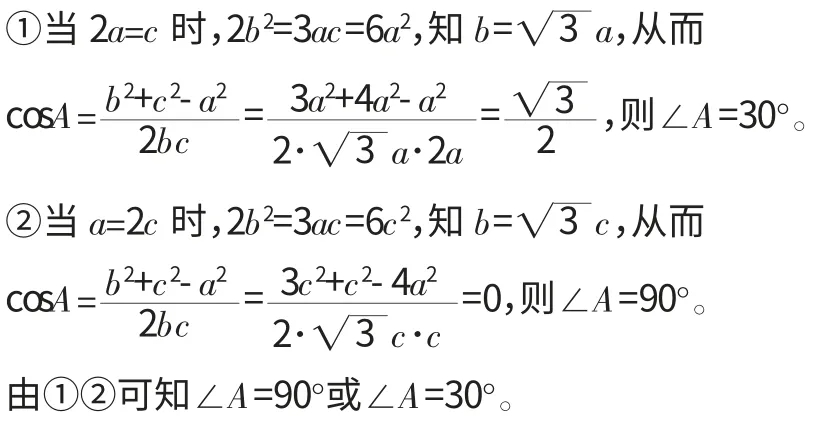
通法二、化边的关系为角的关系。

解：由题意知2B=A+C，且A+B+C=180°，知∠B=60°，则A+C=120°.

由2b2=3ac及正弦定理知2sin260°=3sinAsinC知sinAsinC=

从而∠A=90°或∠A=30°。

解三角形的问题，学生容易想到的是边角之间关系的互化，无论是化为边的关系，还是角的关系，都是可以解决的。要让学生能够想到，敢于去尝试，学生才能掌握和应用。

事实上，教师炫耀自己解法的高明和技巧的高超只会让学生望而却步，容易让学生误以为自己很笨，失去数学学习的兴趣和信心。怎样做到自然？拿到题目，应该自己先做一做，不应该马上就看答案，照本宣科，这样你是无法做到自然，也无法走进学生的思维世界。

培养学生的解题思维能力，我认为有以下几种途径：

1.加强对概念的理解和应用

让学生明白高中数学所有教学内容最基本的是概念。概念是思维的基本形式，具有确定研究对象和任务的作用。《普通高中数学课程标准》指出：教学中应加强对基本概念和基本思想的理解和掌握，对一些核心概念和基本思想要贯穿高中数学教学的始终，帮助学生逐步加深理解。

概念的由来能让学生参与的，要创造条件让学生去动手、去观察、去发现和归纳总结。比如，在椭圆概念的教学中，我利用硬纸片、针和线做了一种道具，用针扎在硬纸的两个点上，这两个点就作为椭圆的焦点，弄上一段线，让线的长度大于两个定点之间的距离，让学生亲自操作，画出了不同形状的椭圆，学生很有心得体会；然后让学生把线的长度缩短，和两定点的距离一样再去观察，学生轻而易举地就给出了椭圆的定义，使课堂教学取得了良好的教学效果，并且学生每见到“椭圆上一点P”时就能想到“P到两焦点距离之和为定值”这一结论，并能灵活地转化成式子。

2.挖掘题目中的隐含条件

数学解题中最首要的问题是读懂题目，挖掘出隐含条件。所谓的隐含条件是指数学题目中那些若明若暗含而不露的已知条件，或者从题设中不断发现并利用条件进行推理和变形而重新发现的条件。一般来说，隐含条件通常隐蔽在数学定义与性质中；或者隐蔽在函数的定义域与值域之中；或者隐蔽在几何图形的特殊位置上；或者隐蔽在知识的相互联系中。

解题活动中，许多学生由于对隐含条件的关注不够或不知道如何挖掘题目中的隐含条件，而使解题活动陷入困境，或导致解题失误，或使思路复杂化。隐含条件的挖掘离不开有效的阅读，从题干中的蛛丝马迹分析出隐含条件，给解题带来畅快淋漓之感。

例如：如果a，b，c成等比数列，那么函数y=ax2+bx+c的图像与x轴的交点个数为 （ ）。

A.0 B.1 C.2 D.1或2

在此题中，条件“a，b，c成等比数列”都能转化成b2=ac，而对于“a≠0”则往往分析不到，不能明确函数y=ax2+bx+c就是一个二次函数。判断函数y=ax2+bx+c的图像与x轴的交点个数只需验证判别式即可。

再比如：lga，lgb，lgc成等差数列是a，b，c成等比数列的（ ）。

A.充分条件 B.必要条件

C.充要条件 D.既不充分也不必要条件

在此题中，“lga，lgb，lgc成等差数列”的等价转化不仅仅是“2lgb=lga+lgc”，还有就是a，b，c>0。

在做题中，有些题目的表述不那么直白，需要我们用一双慧眼看出隐含在文字中的条件；根据解题的实际需要，有效转化题目中的条件，整合有用的信息，确定正确的理解途径，养成良好的思维习惯，就能破解复杂多变的数学问题。

3.要养成“三思而后行”的习惯

一思：要我做什么？就是要对解决的问题进行思考，定位题目考查的知识点，提炼解决问题的基本途径，即分析结论；

二思：我要做什么？就是探讨解决问题的基本途径、步骤，共分为几步，每一步解决什么问题，即分析思路；

三思：给了我什么？即审视条件，把已知条件朝结论方向转化和挖掘，促进学生在条件和结论之间建立联系，及分析条件。

要我做什么？求（f2）；

点评：此方法有具体的式子，学生容易接受。

点评：此法较为抽象，但也是通法，要求程度稍好的同学掌握。

解题应该跟着感觉走，自然至上。自然的想法才是最真实的，是学生能够想到的。所谓自然，就是尽量利用基本知识和基本技能，尽量反映解题的思维历程，解题是一种思维性很强的活动，解题的目的在于启迪心智，锻炼思维，不仅仅是为了解题而解题，而应该紧贴自己的思维实际，让解题思路自然地流淌。

方厚实.专题复习的“四查”“三思”“一练”，中学数学教学参考：上旬，2012（08）.