基于神经网络的热轧机各机架出口比例凸度预报

王文景，侯建新，杨 荃，王晓晨，何 飞

(1.北京科技大学冶金工程研究院，北京 100083;2.北京科技大学国家板带生产先进装备工程技术研究中心，北京 100083)

0 前言

板形质量是衡量带钢质量好坏的一项重要指标。热带钢轧机进行板形预设定时，须遵循一定的调控策略。根据板形控制目标的不同，目前常用的板形调控策略有三种:以精轧出口凸度作为目标;以精轧出口平坦度作为目标;考虑凸度与平坦度之间的耦合关系及板形调控手段的多样性，将精轧出口凸度与平坦度结合起来进行多目标优化控制，该策略应用较多。热带钢轧机进行板形预设定的第一步就是各机架出口目标凸度分配，且目标凸度分配的原则决定了整个板形控制模型调控策略的主体思想［1］。

采用最多的就是基于Shohet 判别式的精轧机架比例凸度分配策略，即根据末机架所测得的带钢出口凸度和厚度，借助等比例凸度原则，分配每个机架的比例凸度值。由于考虑到带钢横向流动的影响，上游机架可以在一定范围内不遵循等比例凸度原则。最终，通过各个机架的凸度分配值计算所需的弯辊力，根据板形控制系统，达到凸度控制的目的。

但是Shohet 判别式也存在不足，如阈值的确定是根据大量的数据统计归纳得来，这能够保证普通规格带钢的计算，但不适用于所有规格的钢种。如果调整参数，需要很大的计算量，给现场造成很大麻烦。本文采用基于神经网络的智能算法，只要给出好的样本库，就能得到准确的预报值，避免繁琐的计算，从而提供出解决凸度分配问题的新思路。

1 传统解析模型的比例凸度分配策略

在热轧中，判别带钢是否出现外观可见的浪形，常采用Shohet 判别式［2］如下:

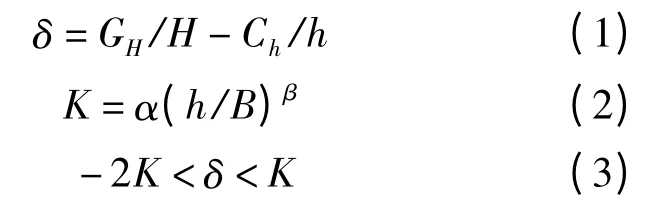
式中，CH/H为入口带钢截面的比例凸度，即入口凸度CH与入口厚度H 之比;Ch/h为出口带钢截面的比例凸度，即出口凸度Ch 与出口厚度h之比;δ为入口带钢比例凸度与出口带钢比例凸度的残差;K为阈值;B为带钢宽度;α、β为常数，α=40，β=2［3］或1.86［4］。

当某机架中带钢出口与入口的比例凸度之差满足式(3)时，则不会产生浪形。式(2)又称为“平坦死区”，当δ ＞K 时，将出现中浪，当δ ＜－2K 时，将出现边浪。如果能使出口带钢截面与入口带钢截面保持几何相似，则出口带钢比例凸度与入口带钢比例凸度相等，此时δ=0，轧出的带钢将是完全平坦的。

由式(1)可知，随着厚度h 的减小，要想不导致浪形，带钢比例凸度的可改变量越小，即“平坦死区”越来越窄。

在进行具体设定时，把精轧机组分成三个区间，分别为凸度调节、平直度保持以及平直度控制。对于七机架热连轧来说，一般F1～F3为凸度调节阶段，通过F1～F3 的凸度调节，并根据Shohet 判别式，使F3 出口达到目标比例凸度，同时又获得较好的板形;F4～F6为平直度保持区段，严格保持比例凸度恒定。

根据Shohet 板形判别原理，在上游机架，由于带钢厚度较厚，带钢比例凸度的可改变量较大，即所谓的“平坦死区”范围较大。因此在进行目标凸度分配时，在上游机架适度偏离等比例凸度相等的控制条件，充分发挥上游机架的凸度控制能力，形成所需要的出口带钢凸度;而在下游机架，严格按等比例凸度相等原则进行控制。通过这一策略，可使得凸度与平坦度得到兼顾控制。但在实际控制中，做到完全按等比例分配有些难度;另外，是通过K.N.Shohet 利用切铝板的冷轧实验数据和不锈钢板的热轧实验数据，导出β 值，能够作为大多数钢种的判定依据，但对于极限规格钢种，如集装箱板SPA－H 等，所得的计算结果精度并不高，为此则需要通过不断实测数据来调整β 值，这给现场造成了很大麻烦。

2 基于神经网络的比例凸度预报模型

用神经网络来预报比例凸度，其精度主要取决于样本库的大小。在实际应用中，神经网络会每周训练一次，将上周测得的实际值作为下一周训练的样本库，这样在日积月累的过程中，神经网络会逐步完善，能够适应不同规格，不同钢种的输入参数，并预报出和实际值误差很小的预测值。

2.1 BP 神经网络

误差反向传播网络(Error Back Propagation Networks，简称BP 网络)是目前使用最广泛的一种人工神经网络，对轧制过程进行数据分析时大多采用BP 网络。它结构简单，工作状态稳定，是一种有导师监督学习的误差反向传播训练算法的多层前馈神经网络［5］。

BP 神经网络是由一个输入层、一个输出层和一个或多个隐层组成，每一层有若干个节点，为多层映射结构。在3 层神经网络结构中，输入层样本为Pi(i=1，2，3，…，m)，输出层目标为Tk(k=1，2，3，…，n)，即为教师信号，实际输出为Tk。Wji和Wkj，分别表示输入层与隐层之间、隐层与输出层之间的连接权，通常采用传递函数Sigmoid，即

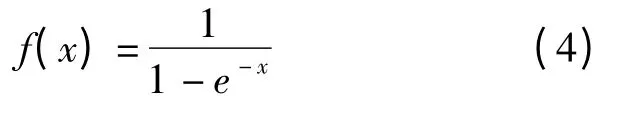
当隐层神经元数目足够多时，BP 神经网络可以任意值精度逼近任何一个具有有限间断点的非线性函数。BP 网络利用均方误差和梯度下降法来实现对网络连接权值的修正。对网络权值修正的目的是使网络实际输出与目标输出之间的均方误差(MSE)达到期望误差范围之内［6］［7］。

2.2 RBF 神经网络

RBF 网络的结构与多层前向网络类似，是单隐含层的前向神经网络。输入层由信号源节点组成;隐含层的单元数由所描述问题的需要而定;输出层对输入的作用做出响应。

RBF 神经网络的主要功能在于能以任意精度逼近任意连续函数，由输入到输出的映射是非线性的，而隐层空间到输出空间是线性的，从而大大加快了学习速度。RBF 网络的输出如式(5)所示

式中，n为隐层节点的个数;wk(k=1，2，…，n)为隐层节点与输出层节点的权值;Xk为第k 个输入向量;φ为高斯函数;Ck(k=1，2，…，n)为第k 个基函数的中心;σk决定了该基函数围绕中心点的宽度;| | Xk－Ck| | 表示Xk与Ck之间的距离。

图1 网络结构图Fig.1 Structure of Network

在板带轧制过程中，为了满足现场的实时性，要求预测模型的修正和控制量的求解是在线进行的。

在RBF 网络中，输入层节点到隐含层节点实现从X→αj(X)的非线性映射，而隐含层节点到输出层节点是简单的线性函数［8］。

αj(X)选用高斯基函数，即

式中，Cj是第j 个基函数的中心点;σj决定了输入变量围绕该基函数中心的离散性，即标准差;‖X－Cj‖是向量X→Cj的范数，表示X 和Cj之间的距离;φj是一个径向对称的函数，它在Cj处有一个唯一的最大值。随着‖X－ Cj‖的增大，φj迅速衰减为零。对于给定的输入X∈Rn，只有一部分中心靠近X 的处理单元被激活。

2.3 神经网络结构设计

用BP 网络和RBF 网络进行预报的程序设计大同小异，主要步骤如下:1)载入训练数据并归一化;2)建立网络并训练;3)载入测试数据并归一化;4)用建立好的网络进行预报，输出预测值;5)将测试数据的实际值和预测值进行对比，并画出趋势图和离散点图，并评价预报精确度。6)将测试数据的预报值进行反归一化。

BP 网络和RBF 二者需要确定的参数不同。其中，BP 网络主要确定3 个参数:隐层节点数、学习速率、动量因子。而RBF 网络主要确定的是宽度系数［9］。

本文中，BP 网络采用单隐含层结构，网络建立函数是newff，仿真函数是sim。其计算结果的精度评价是工具箱的函数mse，记为perf 值，其值越小，说明神经网络的预报精度越高。方法是将600 个样本十等分，每组60 个样本，取一组用于测试，剩余九组用于训练，这种方法称为交叉验证法，有利于神经网络预报的稳定和精确。具体计算时，BP 网络的节点数经过粗算，取值范围最终定在［26，40］，传递函数包括{'tansig'，'purelin'}、{'tansig'，' logsig '}、{'logsig'，' purelin '}，学习速率介于［0.01，0.1］，动量因子介于［0，1］。

由于有六个机架，因此设计了六个独立的神经网络来对各机架进行预报。六个机架参数设定情况具体见表1。

表1 BP 神经网络最佳参数Tab.1 The best parameters of BP network

RBF 神经网络由newrb 函数建立。由于newrb 函数属于approximate 类型，所以不需要手动确定隐含层神经元的数量，RBF 神经网络会在自适应过程中不断增加神经元的个数，提高精度，最终收敛在目标误差范围之内。对于RBF网络来说，我们需要确定的参数就是其spread值，即神经网络的宽度系数。

从基函数原理我们可以知道，每一个RBF网络都只有一个最优的spread 值，将goal 值设定为10－6，在迭代过程中逐渐增加隐层节点数，直到误差低于goal 值则停止迭代。与BP 网络相似，RBF 网络也采用六个独立的神经网络进行预报。六个机架参数设定情况具体见表2。

表2 RBF 神经网络各机架最佳分布密度Tab.2 The best width of RBF network in each stand

3 实验结果及仿真

实际仿真结果是从现场采集的非样本库的60组数据，通过对这60组数据的预报值的分析来最终评价神经网络的精度。

3.1 Shohet 判别式下设定值评价

现场的凸度仪都安装在末机架，因此测量的都是末机架的出口凸度和厚度。根据等比例凸度的原则，下游机架严格保持等比例凸度，再用Shohet 判别式来判断是否能够保证在“平坦死区”内，如果能够满足，则说明判别式良好;如果不能，但又没有出现外表可观的浪形，则说明β 值的设定存在问题，不能够满足现场要求。(－2k，k)的区间范围和残差如图2 所示。

图2 F6 机架平坦死区与实际比例凸度残差对照图Fig.2 Comparsion of the flat area and the actual proportion crown residual error in F6 stand

从图2 中可以看出，残差δ 位于(－2k，k)之间的带钢数很少，经计算得知只有12%。但是现场所实测的这些钢卷的平直度命中率都在90%以上。这说明了用Shohet 判别式来进行比例凸度分配并不符合现场实际情况。

3.2 基于神经网络的比例凸度预报

本文的神经网络预报是用BP 网络和RBF 网络分别进行比例凸度预报，比较二者的预报结果。根据BP 网络局部最优和RBF 网络全局最优的特点，取二者计算的均值作为最终计算结果。样本库采用在进行神经网络预报之前要进行样本库的筛选，剔除其中的异常点。具体方法是根据“3σ 原则”和现场实际情况。其中“3σ 原则”是使用Excel 自带函数average 计算各组输入量的平均值作为其期望值E，然后使用stdevp 来计算其标准差σ，然后确定3σ 范围，即(E－3σ，E+3σ)，以此为依据剔除所有区间外的点。

接下来便是确定神经网络的输入和输出参数。在研究了影响机架出口比例凸度的影响因素后，最终确定神经网络的输入参数有带钢出口宽度、带钢出口厚度、中间坯凸度、精轧出口目标凸度、各机架的综合辊缝凸度、各个机架的压下率、各个机架的轧制力等共22 个参数。而输出参数是F1～F6 各机架的出口比例凸度等6 个参数。

3.3 仿真结果

为了证明训练好的神经网络精度能够满足实际应用要求，需要采集不同于样本库的未知数据来进行拟合对比验证。共采取了60组数据，由于篇幅限制，计算结果如图3 所示。

图3a为BP 网络拟合的结果，图3b为RBF网络拟合的结果。从图中可以看出，对于同一组测试样本的预报，BP 网络和RBF 网络的预报结果趋势大体相当，拟合精度上BP 网络略高于RBF 网络。但就具体情况，能否满足现场实际要求，还需要进行分析。

3.4 结果分析

从图3 看出，曲线头部误差较大，这是因为这三组钢卷厚度超过了10 mm，神经网络训练数据不足，造成预报精度不高。剔除起始3组厚度超过10 mm 的钢卷，从剩余57组测试数据中取出所需要的参数，分别用已经训练到最优的BP和RBF 进行预报，并求出两种网络预报结果的平均值。然后将BP 预报值、RBF 预报值和平均值等三组仿真值分别与实测值进行对比，求各自均方差平方和，取误差最小值作为最终预报结果，从而能够找出最合适的参数来进行实际数据的预报。这种方法与神经网络工具箱函数mse，即均方误差性能函数对应，记为perf，perf 值越小，则说明神经网络的预报精度越高。

图3 神经网络测试值和实际值比较Fig.3 Comparison of Test Value and Actual Value

表3为BP 网络与RBF 网络和二者预报结果均值相比，BP 误差小，因此选用BP 网络的预报结果作为最终输出结果。误差结果如图4所示。

表3 测试值和实际值误差平方和Tab.3 The import parameters of the 10 data bases

图4 BP 网络出口凸度值预报误差分布图Fig.4 Error Distribution of BP network

神经网络输出结果是各机架的出口比例凸度，因此要乘以各自机架出口厚度才能得到出口凸度。从图4 中可以看出:在厚度介于2～6 mm的所有钢卷，处于±4 μm 的误差范围内的钢卷数达到了98%。并根据该钢厂的习惯，凸度公差一般均为±15 μm，充分说明了神经网络预报值完全满足实际需要。

在实际应用中，神经网络每周训练一次，上周根据预报值计算出的实际值会作为下一周神经网络训练的输入样本，随着轧制的深入，神经网络会随着样本库的增加而逐渐提高精度。

4 结论

本文给出了以下两个结论:

(1)通过对基于Shohet 判别式的凸度分配策略的验证，发现在没有出现外观可见的浪形的条件下，末机架入口和出口比例凸度残差能够保证在“平坦死区”内的比例只有12%，充分说明了判别式不能够作为该现场的计算依据。

(2)在BP 网络、RBF 网络和二者均值的预报结果的比较中，BP 网络的预报精度最高。结果表明，厚度在2～6 mm 的钢卷，均能够保证在误差范围之内，能够满足现场要求。

［1］郭德福.热带钢轧机板形控制模型在线数值求解方法研究［D］.北京:北京科技大学，2012.

［2］姜丽丽.热连轧板形设定模型优化与控制［D］.沈阳:辽宁科技大学2012.

［3］K.N.Shohet，N.A.Townsend.“Flatness control in plate rolling”［J］.Journal of the Iron and Steel In stitute，1971(10):769.

［4］Robert R.Somers et al，“Verification and applications of a model for predicting hot strip profile，crown and flatness”［J］.Iron and Steel Engineer，1984(9):35.

［5］刘东东.基于神经网络的热连轧精轧机组预报模型研究［D］.济南:济南大学，2007.

［6］张继先.神经网络及其在工程中的应用［M］.北京:机械工业出版社，1998.

［7］李实，乔爱民，叶乃威，等.［A］.基于BP 神经网络的不锈钢轧制力预报模型研究.2007 年全国多辊冷轧技术研讨会［C］.北京:北京科技大学，2007.

［8］张秀玲，陈丽杰，逄宗朋，等.RBF 神经网络的板形预测控制［J］.智能系统学报，2010，5(1):70.

［9］张敬伟.基于智能算法的热连轧板形设定模型的研究［D］.北京:北京科技大学，2007.