预应力混凝土连续梁桥施工仿真研究

周志强

（山西省交通科学研究院，山西 太原 030000）

1 施工过程模拟分析方法

1.1 正装计算法

正装计算是指为保证桥梁结构成桥后的受力状态计算的准确性，参照实际的结构配筋状况以及施工方案逐步进行计算。正装计算法必须对照设计方案，按照一定的程序分析各阶段的内力。但是，因为在进行分析的过程中，结构节点坐标将会发生变化， 所以它最后设计出来的结构线形与实际状况相差较大[1]。

1.2 倒装计算法

倒装计算是指根据桥梁加载的逆顺序对桥梁结构进行计算，从而得出桥梁结构最为理想的施工方法和受力情况。但是采用倒装计算，难以分析时差效应对桥梁结构的影响[2]。

2 算例及讨论

2.1 预应力混凝土连续梁桥有限元模型的建立

该预应力混凝土连续梁桥位于山西省境内，主路桥宽19.5m，辅路桥宽11.75m，主路桥和辅路桥分隔带为5m，跨度为55m+80m+55m。对于2号块-7号块箱梁采用悬臂浇筑的施工方法，而0、1号块箱梁采用托架现浇的施工方法。设计车速主路为100km/h，辅路为50km/h，对于设计荷载，汽车—超20级，挂车—120，对于人群荷载3.5 kN/m2；地震荷载设计按7度设防。使用大型桥梁软件《桥梁博士》以及有限元软件MIDAS 对桥梁的结构进行计算，在此过程中分别运用的是梁格法和板单元法建立模型。采用的计算方法为正装计算法、倒装计算法。这样做的主要目的是为了使得施工过程中各阶段的结构行为状态得到有效控制，最终符合施工要求。采用MIDAS 计算时将主、辅桥顶板沿梁各节段纵向分为2个单元，横向分为8个单元，底板4个单元，腹板沿梁高方向分为2个单元，主、辅桥各计2808个单元，1948个节点。采用桥博计算时将主、辅桥沿梁横向分为2个梁格，沿梁纵向每节段分为1个梁格，主桥共计187个单元，辅桥共计126个单元。参考定性分析，对桥梁施工程序加以确定，同时依据计算出来的结果，得到具体的施工工序。每施工梁段分挂篮前移、混凝土浇注和预应力张拉3个工况，整个结构形成过程共分为52个施工阶段和1个运营阶段。这样一来，整个施工过程中出现的荷载、边界条件、计算图式的改变都能在有限元模型中得到准确的体现。全桥理论计算模型如图1（MIDAS）、图2（桥博)所示。

图1 全桥理论计算模型(MIDAS)

图2 全桥理论计算 模型(桥博)

2.2 桥梁各节段挠度的正装及倒装分析

按照之前的正装及倒装计算方法， 并且结合有限元计算模型，可以得到如下3种结论[3]：（1）仅仅考虑预应力作用下的各节段挠度；（2）仅仅考虑自重作用下的各节段挠度；（3）考虑自重、预应力、徐变作用下的节段挠度。表1显示采用Midas和桥博两种有限元模型的挠度计算结果。根据上表数据，我们可以发现，这两种方法计算得出的数值是比较接近的。这说明，计算准确度较高。从墩顶O号块开始施工的悬臂结构，受到施工设备自重、节段自重、混凝土收缩徐变等各方面的影响。因此，采用正装计算能够有效的计算出各个阶段下的结构变形及内力，可以及时地计算出误差，以及迅速得到控制之后的结果。

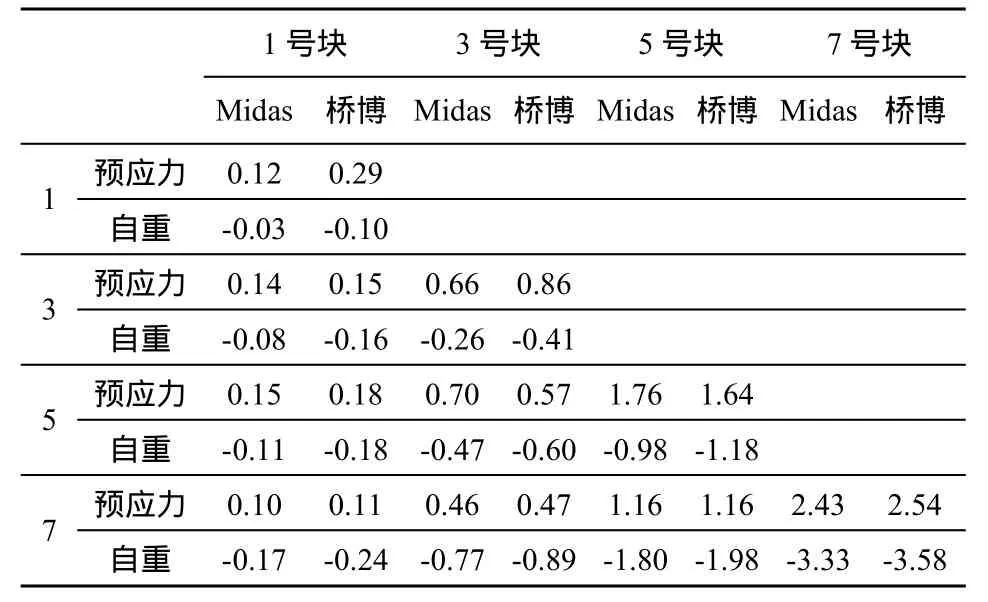
表1 自重和预应力作用下各节段挠度Midas和桥博计算结果比较

2.3 收缩徐变后各节段挠度的正装及倒装分析

正装计算是对桥梁的直接模拟，根据桥梁施工的顺序进行计算，同时考虑每个节段的收缩徐变。倒装计算则是逐步拆除单元，对拆除单元接缝处的主体加以模拟。由于倒装计算模拟的特性，所以采用倒装计算是无法完成混凝土的收缩徐变计算。为解决这一问题，需要运用以下方法加以解决：进行正装计算时，暂不考虑混凝土收缩徐变这一因素，首先计算结构的变形值和内力，算出相应数据后，再对收缩徐变后的变形值进行计算。最后，运用倒装计算的方法，扣除正装计算时各阶段混凝土时效的影响。

2.4 正装计算与倒装计算的关系

对预应力混凝土连续梁桥有限元模型进行相关的倒装计算，得出只考虑自重作用下的各节段的倒装计算挠度，如表2所示。将表2和表1进行对比，可知，采用倒装计算时表2中7号块在仅考虑自重作用下倒装分析的挠度与表1中7号块的挠度是一致的；而表2中5号块的挠度为表1中5～7号块挠度的和；表2中3块的挠度为表1中3～7号块的和；表2中1号块的挠度为表1中1～7号块挠度之和。若采用正装计算，则各节段的挠度是表1中相应节段的迭加，比如说3号块自重作用下的挠度，则为1～3号块自重共同作用在3号块的挠度之和，以此类推。对于涉及到预应力和徐变的情况，只需在计算每个节段挠度的时候，将对应的影响值计算进去。

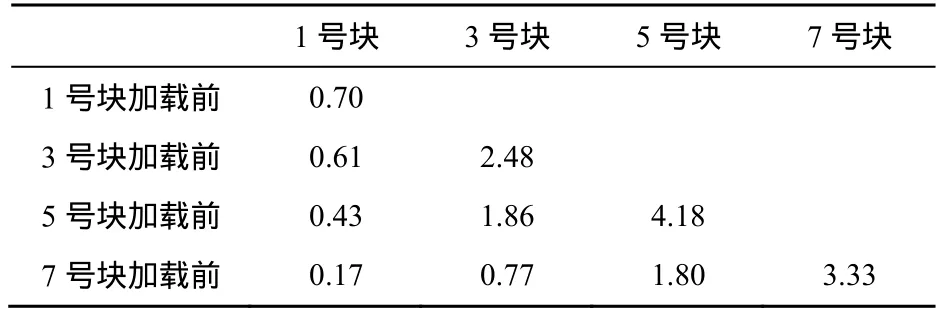
表2 仅考虑自重作用下倒装分析各节段挠度

3 结论

在预应力混凝土连续梁桥施工控制仿真计算的过程中，采用正装与倒装计算相结合的方法，可以较为全面的考虑到混凝土收缩徐变、几何非线性以及初始应力的影响，有利于得到较为准确的预拱度，确保施工质量。

[1]吕建鸣, 陈云海.预应力混凝土桥梁徐变计算方法的研究[J].公路交通科技.2005(07)：61-66.

[2]谭德盼.预应力混凝土连续梁桥施工控制技术与应用[D].广州：广东工业大学.2007..