积分因子的存在性及求法论析

白星华（阳泉师范高等专科学校，山西 阳泉 045200）

积分因子的存在性及求法论析

白星华
（阳泉师范高等专科学校，山西 阳泉 045200）

积分因子法的起源相对较晚，但是其对于求解常微分方程的作用却是相当巨大的。要想将一般的常微分方程转变成全微分方程的形式，最重要的一个步骤就是求出积分因子。文章对积分因子的存在性及求法进行了论述。

常微分方程；积分因子；恰当方程

1　研究意义

积分因子法是求解常微分方程的一种常用解法。通过本文对于积分因子法的讨论和分析，希望能够给读者提供更为清晰的积分因子法求解常微分方程的思路。

2　积分因子法的解题思路

介绍形如的积分因子法求解。

3　二元微分方程积分因子的存在性及求法

3.1二元微分方程积分因子的概念

3.2积分因子的存在性

上面的式子可以简化为

3.3积分因子的求法

积分因子的求法主要有公式法、分组法和观察法，观察法比较简单，不再赘述。

3.3.1公式法

方程（2.1）存在形式如μ（x）的积分因子的充要条件：

φ的自变量只和y有关；

3.3.2分组法

也可以说微分方程

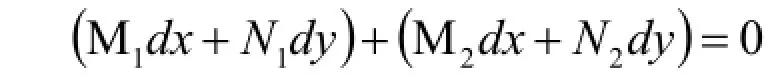
μ1是前一个式子的积分因子，即

μ2是第后一个式子的积分因子，即

从中选择满足的和，其中为关于μ1，μ2的连续可微函数，于是便是原方程的积分因子。

4　结论

积分因子法的关键步骤是求解积分因子，在求解积分因子之前先要判断方程是否存在积分因子，确定存在后再按照步骤进行求解。积分因子的求法常见的方法有公式法、分组法及观察法，在此需要强调的是，三种积分因子的求法不存在孰优孰劣，在求解积分因子前必须合理选用积分因子求解方法。

［1］王高雄，周之铭，朱思铭.常微分方程.高等教育出版社，2006. ［2］陈吉美.积分因子及其应用.湖南工业大学学报［J］.2010， 3（2）：15-16.

［3］王金诚.浅析积分因子的求法.中国科技信息［J］.2007（10）：25-26.

（责任编辑：黄密）

Analysis of the existence and solving method about integral factor

BAI Xing-hua
（Yangquan Teachers’College，Yangquan Shanxi 045200）

Origin of integration factor relatively late，but its role for solving ordinary differential equations is quite enormous.To convert ordinary differential equation ODE sake，the most important step is to determine the integral factor.The article Integrating Factor Existence and Seeking discussed.

ordinary differential equations；integrating factor；appropriate equation

O12

A

10.3969/j.issn.1672-7304.2015.03.031

1672-7304（2015）03-0073-02

白星华（1981-），女，山西平定人，讲师，研究方向：数学教育，基础数学。