基于RSSI 的自适应分段曲线拟合室内定位算法*

林方旭，朱明华

(华东师范大学 软件学院，上海200000)

0 引 言

无线传感器网络(wireless sensor networks，WSNs)被誉为21 世纪最有影响力的21 项技术和改变世界的10 大技术之一［1］。在室外定位系统中，全球定位系统(global positioning system，GPS)已被广泛用于国民经济各个领域。GPS信号无法穿透建筑物等障碍物，不适用于室内定位。但基于无线传感器网络的室内定位技术正好弥补了GPS 室内定位的不足，可以为会展中心、地下停车场等场所提供实时的位置和导航信息。

本文针对现有定位算法精度不高、难以满足不同室内场合的问题，提出自适应分段曲线拟合定位算法。结果表明:与均值滤波单一拟合相比，本文算法的平均定位误差提高了0.4 m，与高斯滤波单一拟合相比平均定位误差提高0.2 m。

1 系统与算法总体介绍

定位系统由信标节点(坐标已知)、未知节点以及PC处理终端组成。传感器节点(信标节点和未知节点)均采用TI 的CC2430 芯片搭建而成。信标节点以固定发射功率(0 dBm)发送数据包，并发送自己的ID(ID 与物理坐标相对应)，未知节点将接收的数据包通过RS—232 转USB 接口上传到PC 端［5］。PC 端对上传数据进行预处理，并建立自适应分段曲线拟合的室内信号传播模型，最终实现定位。

2 RSSI 预处理

由于室内信号存在多径传播现象，接收的原始RSSI 数据中会存在部分异常值，这些异常值会干扰定位结果。因此，需对原始RSSI 数据做滤波预处理。

高斯滤波预处理是先对采样的RSSI 数据进行高斯滤波，然后再选取高概率发生的RSSI 值，并对选取的RSSI 值进行均值滤波。高斯分布函数为

其中

高概率发生区间为［0.6，1.0］(0.6 为经验值)，根据式(4)、式(5)将滤波后选取的RSSI 值再进行均值滤波，即为当前RSSI 值。

利用Matlab 对原始RSSI 数据做高斯滤波预处理，如图1所示。图1 表明滤波前RSSI 值存在一定的波动，部分数值严重偏离正常波动范围，经高斯滤波后的曲线变得平滑，RSSI 值趋于稳定。

图1 采样数据经高斯滤波处理效果Fig 1 Sampling data processing effect by Gaussian filtering

3 自适应分段曲线拟合

3.1 信号传输模型

目前，常用的信号传播模型为对数距离路径损耗模型—Shadowing 模型，该模型为

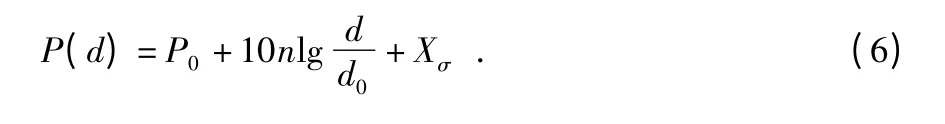
其中，P(d)和P0分别为未知节点在d(m)和d0(m)处接收到的信号强度(dBm)，n 为路径损耗系数，Xσ是均值为0 的高斯随机变量(dBm)。

在实际室内定位中，一般采用简化的Shadowing 模型［6］

其中，A 和n 为环境参数，随着实际室内环境的不同，A和n 的值也随之不同。

3.2 自适应分段曲线拟合传播模型

利用Matlab 绘制预处理后的RSSI 值和d 值之间的二维曲线，并通过线性回归方法计算得到当前室内环境参数A 和n 值，其中，A=－31.46，n=1.70，拟合曲线如图2 所示。

图2 参数优化后的RSSI 测距模型曲线Fig 2 Curve of RSSI ranging model after parameters optimization

图3 表明:RSSI 随着传输距离的增加而衰减，近距离时信号衰减快，远距离时衰减则趋于平缓，但信号衰减曲线仍存在部分不规则的上下抖动现象。而且从4 m 处开始拟合值偏离实测值，所以，单一拟合难以满足复杂室内环境下的定位需求，需根据曲线整体变化趋势进行分段拟合处理［7，8］，以实现更精确的定位。根据图2 变化趋势将1 ～L m(1 ＜L ＜10，且L=1.2，1.4，…，10 m)和L～10 m 分别进行曲线拟合。

由式(7)可得

由式(8)可得未知节点与信标节点间的距离。节点间距离的理论值与计算值之差决定了之后定位的精度。同时，为了满足不同室内环境下的定位需求，提高整体定位精度，本文依据距离的均方误差(mean squared error，MSE)值来确定自适应分段拟合点，从而保证距离计算值的整体精度，如式(9)所示

式中 σ 为距离的均方误差，d1为距离的计算值为距离的理论值。n 为实测的位置数(n=46)。σ 越小，计算值越接近理论值，总体定位精度越高。

经Matlab 仿真表明当前室内环境下自适应分段拟合点在L=7.8 m 处(即当L=7.8 m 时距离的MSE 最小，整体定位精度最高)。利用线性回归方法分别计算出自适应分段拟合曲线的A 和n 的值，如式(10)所示，拟合曲线如图3 所示。与图2 相比图3 更贴近当前室内的环境情况

图3 自适应分段曲线拟合Fig 3 Adaptive piecewise curve fitting

4 定位计算

假定信标节点坐标为(x1，y1)，(x2，y2)，…，(xn，yn)未知节点坐标为(x，y)，再由式(8)中RSSI 和d 的关系和最小二乘法原理得到

其中

5 实验结果与分析

实验在华东师范大学理科大楼A 栋B1 楼15 m×10 m室内环境下进行。其中三个信标节点置于离地面1.0 m处。未知节点从距离信标节点1.0 m 处开始，每隔0.2 m 采样一次，即分别在1.0，1.2，1.4，…，10 m 处采样，总计46 个未知位置。

使用Matlab 对理论值、均值滤波单一拟合、高斯滤波单一拟合、高斯滤波自适应分段曲线拟合作分析比较，如图4所示。图4 表明相比均值滤波单一拟合和高斯滤波单一拟合，高斯滤波自适应分段拟合更贴近理论值，而且在距离较远处(图4 中7.8～10 m 之间)仍有较好的拟合效果，定位结果更准确。

本文的定位算法与均值滤波单一拟合相比定位平均误差提高0.4 m 以上，与高斯滤波单一拟合相比平均定位误差提高0.2 m，且67%以上的位置坐标精度得到改善。其中，在0～10 m 室内环境下均值滤波单一拟合的定位误差在0.15～2.93 m 之间。高斯滤波单一拟合则在0.15～2.55 m之间，本文定位算法的定位误差落在0.08～1.11 m 之间，定位精度得到显著提高，且对远距离能有较好的定位效果。

图4 未知节点坐标定位轨迹图Fig 4 Unknown node coordinate positioning trajectories

6 结 论

本文针对单一的对数距离路径损耗模型拟合难以满足复杂室内环境的不足，提出高斯滤波自适应分段曲线拟合定位算法。通过自适应分段拟合算法(自适应分段拟合点以距离的MSE 最小作为评判标准)得到高斯滤波后RSSI和距离d 之间的关系，最终实现定位。对三种不同定位方法进行了定位误差分析，对比结果表明:本文算法的定位精度最高，且能适应不同的室内环境，能满足日常无线传感器网络的室内定位的需要。

［1］ 李建中，高 宏.无线传感器网络的研究进展［J］.计算机研究与发展，2008，45(1):1－15.

［2］ 章坚武，张 璐，应 瑛，等.基于Zig Bee 的RSSI 测距研究［J］.传感技术学报，2009，22(2):285－288.

［3］ 朱明辉，张会清.基于RSSI 的室内测距模型的研究［J］.传感器与微系统，2010，29(8):19－22.

［4］ 彭玉旭，杨艳红.一种基于RSSI 的贝叶斯室内定位算法［J］.计算机工程，2012，38(10):237－240.

［5］ Kaemarungsi K，Ranron R，Pongsoon P.Study of received signal strength indication in Zig Bee location cluster for indoor localization［C］∥2013 10th International Conference on Electrical Engineering/Electronics，Computer，Telecommunications and Information Technology(ECTI－CON)，IEEE，2013:1－6.

［6］ Adewumi O G，Djouani K，Kurien A M.RSSI－based indoor and outdoor distance estimation for localization in WSNs［C］∥2013 IEEE International Conference on Industrial Technology(ICIT)，IEEE，2013:1534－1539.

［7］ 吴成东，程 龙，张云洲，等.基于循环滤波的无线传感器网络室内定位［J］.控制与决策，2011，26(10):1515－1519.

［8］ 朱明强，侯建军，刘 颖，等.一种基于卡尔曼数据平滑的分段曲线拟合室内定位算法［J］.北京交通大学学报，2012，36(5):95－99.