基于精细分区控制的三电平逆变器中点电位平衡策略
王慧敏 温坤鹏 张 云 夏长亮,
(1.天津工业大学电工电能新技术天津市重点实验室 天津 300387 2.天津大学电气与自动化工程学院 天津 300072)
基于精细分区控制的三电平逆变器中点电位平衡策略
王慧敏1温坤鹏1张 云2夏长亮1,2
(1.天津工业大学电工电能新技术天津市重点实验室 天津 300387 2.天津大学电气与自动化工程学院 天津 300072)
针对中点钳位型(NPC)三电平逆变器中点电位波动问题,在三矢量四状态合成方法的基础上,提出一种精细分区控制的中点电位平衡策略。在低调制度下,对占空比分配因子进行限幅,尽量控制中点电流为零。在高调制度下,通过对比最值电流法和分配因子法分区结果的不同,将工作区域划分为可控区域(CI)、不可控区域(UI)和存疑区域(DI),并对DI区域按中点电流控制效果进行归属判定,在不增加开关频率的情况下,尽可能将中点电流的绝对值控制为最小,实现减小中点电位波动的目的。仿真和实验结果验证了所提策略在降低开关频率的同时,可有效抑制中点电位的波动。
中点钳位型三电平逆变器 中点电位平衡 三矢量四状态调制 精细分区控制
0 引言
牵引逆变器是牵引机车交-直-交变流系统的重要组成部分,随着大功率、高速度运输工具的发展需要,传统的两电平系统逐渐不能满足要求,多电平逆变器成为研究热点[1,2]。中点钳位型(Neutral Point Clamped,NPC)三电平逆变器具有开关频率低、输出电压谐波含量少、功率开关管上电压应力低等优点,成为目前中高压交流领域应用最广泛的多电平变换器[3-6]。然而,由于NPC三电平逆变器直流侧使用两电容分压,工作时易产生中点电位不平衡问题,进而影响逆变系统的稳定运行及输出性能。
针对NPC三电平逆变器中点电位不平衡的问题,文献[7-13]提出了不同的解决方案。文献[14]提出了一种混合调制策略,将三电平空间矢量转换成两电平的形式,简化了计算过程,然后根据不同的调制度区间采用不同的调制方法,实现了对中点电位的精细化控制。文献[15]分析了中点电流对中点电位的影响,通过判断中点电流的最值进行工作区域的划分,在最近三矢量(Nearest Three Vectors,NTV)策略的基础上提出了一种中点电位限幅控制策略,将中点电位波动值限定在最小范围内,从而达到控制中点电位波动最小的目的。文献[16]提出了一种基于虚拟矢量的优化调制策略,将矢量的作用时间都映射到第一扇区,简化了求解矢量占空比的过程,同时利用冗余矢量优化了开关序列。由于虚拟矢量调制方法每个开关序列都有5个开关状态,这使得其总开关频率仍然较高。
牵引变流器运行时要求开关频率低于1 kHz,为了充分利用开关频率,通常采用分频调制策略,低频时一般采用异步空间矢量调制,这使得需要较高开关频率以达到完全控制中点电位平衡的调制方法不再适用,在这种情况下,只能在降低开关频率的基础上,尽量削弱中点电位的不平衡状态。为此本文在三矢量四状态合成方法的基础上提出了一种基于精细分区控制的中点电位平衡策略。当调制度0
1 NPC三电平逆变器空间矢量调制
1.1 NPC三电平逆变器
图1为NPC三电平逆变器的拓扑结构图,由于三电平电路每相可输出p、o和n三种电平,三相共输出33=27种电平组合,对应27种开关状态。
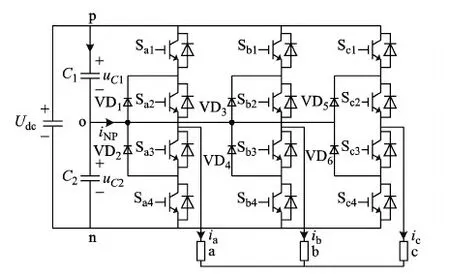
图1 NPC三电平逆变器拓扑结构
在α-β平面上的空间矢量图中,多个开关状态可能对应同一个基本空间电压矢量,称这样的开关状态为冗余状态。空间矢量分布如图2所示。

图2 空间矢量图
按照矢量的模长可将空间矢量分成大矢量、中矢量、小矢量和零矢量4类。其中零矢量对应3个冗余状态,本文调制策略零矢量只选用ooo开关状态。大矢量和零矢量作用时产生的中点电流为0,中矢量和小矢量作用时产生变化的中点电流。每个小矢量对应2个冗余状态,产生的中点电流大小相等、方向相反。
1.2 NTV策略中点电流分析
图3为第一扇区的空间矢量图,其中ic、-ic、ib、ia和-ia为各矢量产生的中点电流。采用NTV方法,当参考电压矢量位于小三角形3中时,由伏秒平衡原理可知
(1)
式中:Vref为参考矢量;VS0、VM、VS1分别为与参考矢量距离最近的3个矢量;dS0、dM、dS1分别为三矢量的作用时间占空比。

图3 第一扇区的空间矢量图
小矢量VS0所对应的开关状态有两个,其中onn产生的中点电流与图1中iNP的参考方向一致,称VS0(onn)为正小矢量;poo产生的中点电流与iNP的参考方向相反,称VS0(poo)为负小矢量。若设正小矢量VS0(onn)的占空比为(1+kS0)dS0/2,其中kS0定义为VS0的占空比分配因子,其取值范围为[-1,1],可得出对应负小矢量VS0(poo)的占空比为(1-kS0)dS0/2。同理,设正小矢量VS1(ppo)的占空比为(1+kS1)dS1/2,其中kS1定义为VS1的占空比分配因子,其取值范围为[-1,1],可得出对应负小矢量VS1(oon)的占空比为(1-kS1)dS1/2。则一个采样周期内,合成参考矢量Vref产生平均中点电流iNP为
iNP=kS0dS0ia+dMib+kS1dS1ic
(2)
式中ia、ib和ic为负载电流。在一个采样周期内,由中矢量产生的中点电流为
iM=dMib
(3)
在参考矢量和负载已知的条件下,各矢量的占空比及其产生的中点电流都是确定的,故由式(2)可知,平均中点电流iNP的大小仅与小矢量的占空比分配因子有关。对式(2)进行分析可知,当kS0=-sgn(ia)且kS1=-sgn(ic)时,iNP取最小值iNP_l;当kS0=sgn(ia)且kS1=sgn(ic)时,iNP取最大值iNP_h。
当Vref位于小三角形5和6时,最近三矢量中只有一个小矢量,故只需调节一个占空比分配因子,其他扇区与此类似。图4为一个输出周期内iNP_l、iNP_h和中矢量产生的中点电流iM的波形图。
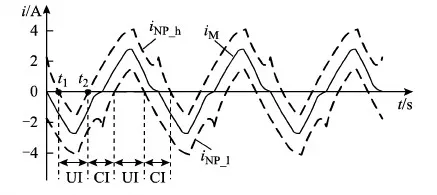
图4 一个输出周期内iNP_l、iNP_h和iM的波形图
2 基于分配因子分区的中点电位平衡策略
2.1 工作区域的判断
令电容容值C1=C2=C,则由图1可得
(4)
(5)
如果在[ta,tb]区间内iNP符号不变,则由式(5)可得
(6)

令iNP∈[iNP_l,iNP_h],由图4可知,当
iNP_h≥0且iNP_l≤0
(7)
时,可控制iNP=0,则称此时Vref位于CI区域,否则称Vref位于UI区域,本文称这种判断工作区域的方法为最值电流法,具体判断方法如表1所示。根据最值电流法判断出的UI区域、CI区域如图4所示。

表1 最值电流法
注意到NTV策略只有在CI区域才能控制iNP为0,因此在判断工作区域时,也可直接令iNP=0,计算出占空比分配因子kS0和kS1。若kS0∈[-1,1]且kS1∈[-1,1],说明利用小矢量能够控制iNP=0,即Vref处于CI区域,否则Vref处于UI区域,本文称这种判断工作区域的方法为分配因子法,具体判断方法如表2所示。

表2 分配因子法
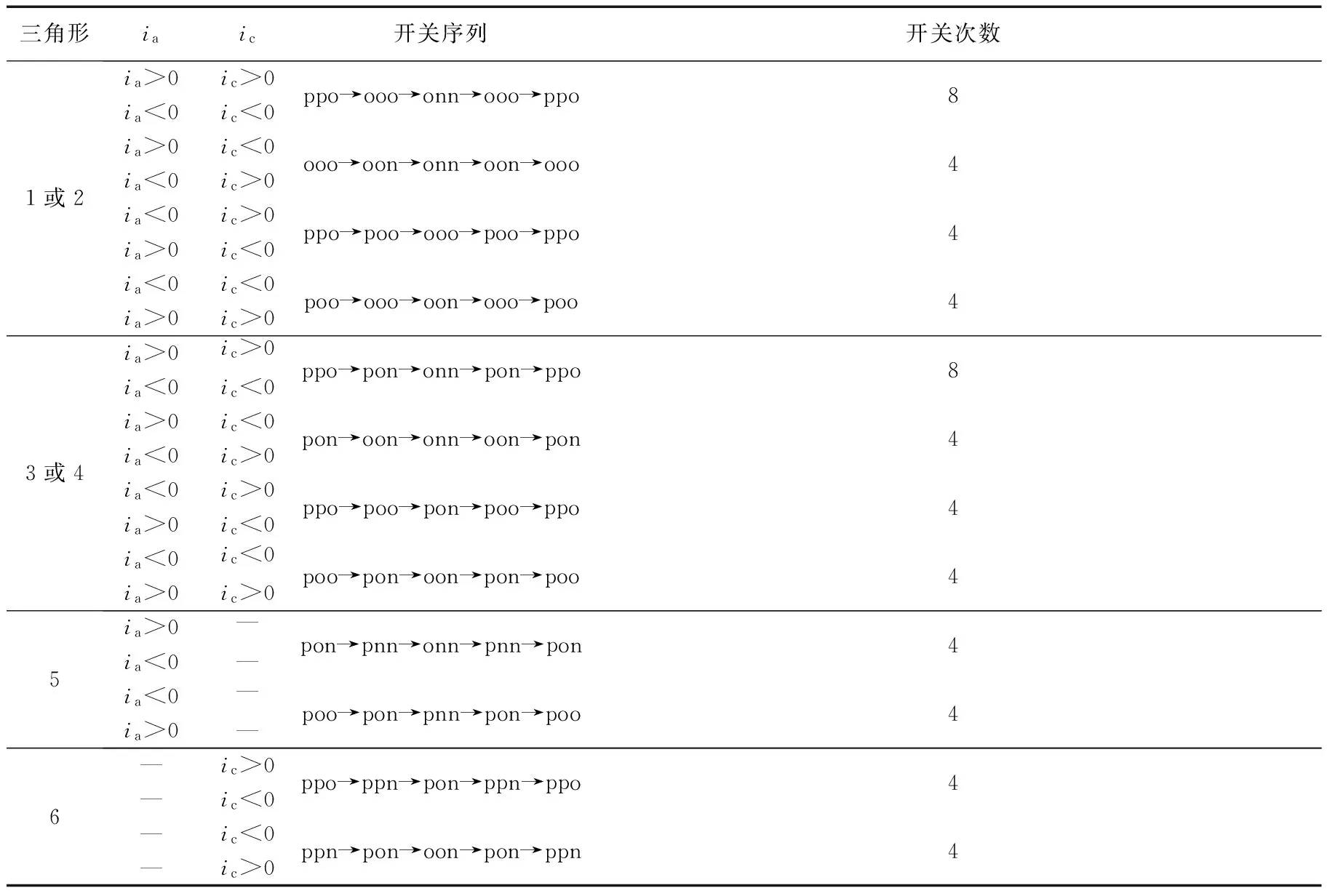
从降低开关频率的角度考虑,NTV策略通常选用三矢量四状态合成方法控制iNP为0,当参考矢量位于1、2、3或4小三角形时,工作区域内有5个可选开关状态,则舍弃一个控制iNP能力差的小矢量冗余状态,并忽略被舍弃冗余状态对iNP的影响。实际上,在一些区域舍弃小矢量冗余状态对iNP影响较大,将导致上述两种分区方法存在判断差异。

对于分配因子法,工作区域按照实际中点电流能否控制为0进行划分,在有5个开关状态的区域,受到舍弃冗余状态的影响,该方法将最值电流法判断出的CI区域中实际不可控区域直接判断为UI区域,相当于在最值电流法判断出的UI区域基础上增加了一部分区域。如果在UI区域控制中点电流为iNP_l或iNP_h,从图4可看出,增加区域内中点电流符号发生改变,因此不能保证其中点电流绝对值最小。该方法判断出的CI区域内iNP能够完全控制为0。
下面根据不同调制度具体分析工作区域的划分方法。
1)当调制度m>0.5时,iNP将受到中矢量的影响。当调制度越大、参考矢量与中矢量距离夹角越小时,中矢量对iNP影响越大,这使得iNP越难以控制,此时被舍弃冗余状态的小矢量的占空比较大,舍弃冗余状态对iNP影响也较大。图5为m>0.5时不同调制度下两种判断方法分别对工作区域的判断结果仿真图,其中灰色粗实线表示最值电流法判断出的工作区域值,黑色细实线表示分配因子法判断出的工作区域值;值取1时表示CI区域,值取2时表示UI区域。
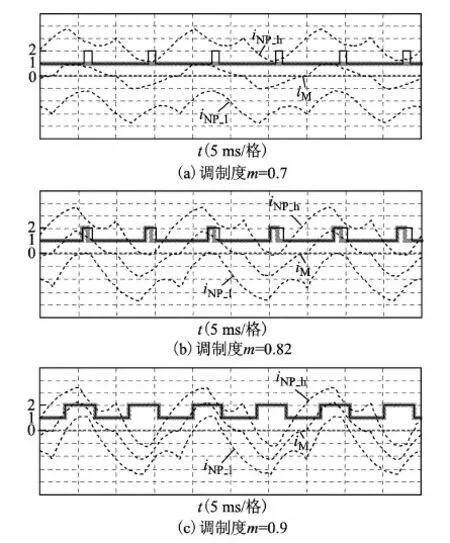
图5 不同判断方法的判断结果仿真图
如图5a所示,当m=0.7时,采用最值电流法判断,工作区域都为CI区域,而采用分配因子法判断,工作区域却存在UI区域。随着m增大,中矢量对iNP的影响变大,在参考矢量离中矢量距离较近的区域开始出现iNP_h<0或iNP_l>0,此时采用最值电流法判断,工作区域开始出现UI区域,然而受舍弃冗余状态的影响,工作区域仍存在差异,如图5b所示。当m=0.9时,两种判断方法的判断结果相同,如图5c所示,说明此时工作区域的判断不受被舍弃冗余状态的影响。本文将受舍弃冗余状态的影响而产生差异的区域称为存疑区域(DI),将工作区域划分为CI区域、UI区域和DI区域3种。
当存在DI区域时,两种判断方法产生的中点电流波形示意图如图6所示。
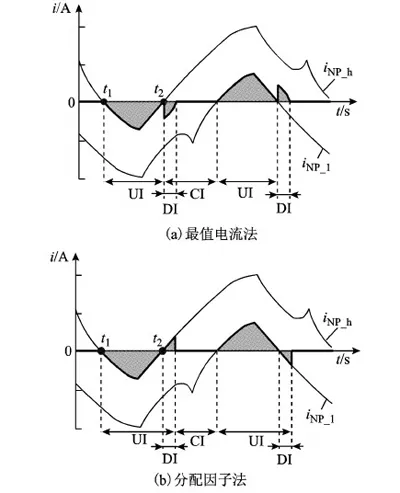
图6 不同判断方法产生的中点电流波形示意图
由图6a可知,应用最值电流法分区时,DI区域包含在CI区域中,DI区域的中点电流为舍弃一个小矢量冗余状态后,由剩余的开关状态控制而产生。由图6b可知,应用分配因子法分区时,DI区域包含在UI区域中,DI区域的中点电流为iNP_h或iNP_l。由此可知,两种不同工作区域判断方法的区别之处在于对DI区域中点电流的控制。为了不增加系统的开关频率,同时将DI区域中点电流绝对值控制为尽可能小,比较两种分区方法在此区域产生的中点电流绝对值,若应用最值电流法产生的中点电流绝对值小,则DI区域归属于CI区域,否则DI区域归属于UI区域。
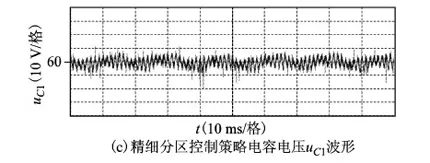
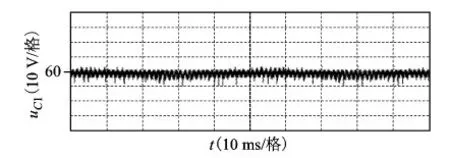
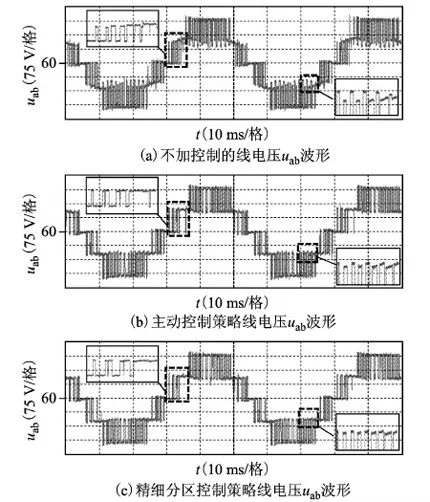
2)当调制度0 2.2 中点电位平衡策略实施步骤 在对工作区域进行区域划分时,需要同时使用两种分区方法。采用三矢量四状态合成方法时,被舍弃冗余状态的小矢量由于只剩下一个开关状态,其占空比分配因子为1或-1,故令iNP=0计算占空比分配因子时,只需求解另一个未舍弃开关状态的小矢量占空比分配因子。此外,分配因子法在计算出小矢量占空比分配因子的同时,即可对工作区域进行判断,比较简便,因此本文在分配因子法的基础上,对工作区域进行精细分区,调制策略实施步骤如下: 1)判断Vref所在的具体小三角形,确定所选用的最近3个矢量。 2)根据伏秒平衡原理计算三矢量的占空比。 3)确定iNP_h、iNP_l、iM及三矢量四状态方法下iNP的表达式,令iNP=0,计算小矢量占空比分配因子kS0或kS1。 当调制度0 当m>0.5时,若采用分配因子法判断工作区域为CI区域,则按照CI区域调制方法控制中点电流为0;若采用分配因子法判断工作区域为UI区域,则需用最值电流法进一步判断:若判断结果同为UI区域,则按照UI区域调制方法进行调制;若判断结果为CI区域,说明参考矢量位于DI区域,需将两种判断方法产生的中点电流绝对值进行比较,如果应用最值电流法产生的中点电流绝对值小,则将工作区域归属为CI区域,否则归属为UI区域。CI区域调制方法和UI区域调制方法具体如下述所示。 2.3 CI区域调制方法 在CI区域内,为了尽量降低开关频率,选用三矢量四状态合成方法,当一个小三角形中含有5个开关状态时,舍弃一个控制中点电流能力较弱的冗余状态。为了减少开关序列的开关次数,本文舍弃的均为正小矢量开关状态,如在第一扇区,对于1和3小三角形,舍弃小矢量VS1的开关状态ppo;2和4小三角形,舍弃小矢量VS0的开关状态onn。这样被舍弃冗余状态的小矢量占空比分配因子均为-1。第一扇区的6个小三角形在CI区域的开关序列如表3所示。 表3 CI区域的开关情况(第一扇区) 以小三角形3为例,其平均中点电流为 iNP=kS0dS0ia+dMib-dS1ic (8) 由式(8)可知,iNP的大小只与占空比分配因子kS0有关。令iNP=0,可得 (9) 若所求kS0满足-1≤kS0≤1,则可判断参考矢量位于CI区域;若不满足,当kS0>1时,令kS0=1;当kS0<1时,令kS0=-1。 2.4 UI区域调制方法 由于中矢量产生的中点电流iM与iNP_l和iNP_h频率相同,且当iNP_l和iNP_h取最大值或最小值时,iM也取最大值或最小值。当iM>0时,调制方法采用产生iNP_l所对应的开关序列,当iM<0时,采用产生iNP_h所对应的开关序列。表4为iNP=iNP_h和iNP=iNP_l时,位于第一扇区的开关情况,其中阴影部分为iNP=iNP_l时的判断条件。 表4 iNP=iNP_h和iNP=iNP_l时的开关情况(第一扇区) 由图4可知,在[t1,t2]区间,当iNP=iNP_h时,两电容电压差的绝对值最小,由式(6)可知 (10) 在确定UI区域、CI区域调制方法后,针对本文工作区域判断方法进行了仿真验证。图7为调制度m=0.82时,由最值电流法切换成所提出的精细分区法时电容电压uC1的变化情况,从图中可知,采用精细分区控制策略后,中点电位波动明显变小,验证了本文所选用的工作区域判断方法的有效性。 图7 m=0.82时电容电压uC1的波形 为验证所提调制策略的有效性和可行性,本文在以DSP28335为控制核心的三电平逆变器实验平台上进行了实验,实验参数如表5所示。其中,考虑到牵引变流器运行时开关频率不能高于1 kHz,且仅在低频时(基波频率为0~20 Hz)采用异步空间矢量调制,故选择基波频率为20 Hz,载波频率为800 Hz。 表5 实验参数 图8为调制度m=0.85时,不同调制策略电容电压uC1的实验波形,其中主动控制策略即为在整个工作区域内均采用三矢量四状态合成方法控制中点电流为0的策略。 图8 不同控制方法电容电压uC1实验波形 图8a为不对中点电位施加控制的电容电压uC1波形,波动峰峰值为21.7 V。图8b为主动控制策略的电容电压uC1波形,波动峰峰值为10.9 V。图8c为本文精细分区控制策略的电容电压uC1波形,波动峰峰值为6.8 V。由此可知,与不对中点电位施加控制的策略相比,本文策略的电容电压峰峰值降低了68.7%;与主动控制策略相比,本文策略的电容电压峰峰值降低了37.6%。因此,精细分区控制策略能更有效地控制中点电位平衡。 为了验证低调制度时精细分区控制策略的有效性,调制度m=0.3时的电容电压实验波形如图9所示。 图9 m=0.3时精细分区控制下电容电压uC1的波形 由图9可看出,低调制度时,虽然此时舍弃的小矢量开关状态占空比较大,但可通过其他小矢量进行弥补,采用所提出的精细分区控制策略可有效抑制电容电压波动,中点电位平衡效果良好。 图10为调制度m=0.85时,不同调制策略输出线电压uab的实验波形。 图10 不同控制方法线电压uab实验波形 由图10可看出,相比已降低开关频率的三矢量四状态主动控制策略,本文精细分区控制策略使用的开关频率更少,同时由于在本文策略控制下中点电位波动更小,输出线电压波形也更为平整。 图11为调制度m=0.85时,不同调制策略输出相电流的实验波形。 图11 不同控制方法输出相电流波形 由图11可看出,不同控制方法下输出电流波形正弦度均较高。不加控制时,由于不同矢量切换最多只有一相开关动作,中点电流波动较少,负载电流连续性较好,波形质量较高;主动控制策略由于舍弃开关状态,存在多相开关动作,因此与不加控制相比,波形质量稍差,但差别不大;精细分区控制策略在生成PWM波时,引入了最大电流、最小电流开关序列,多相开关动作相对于主动控制更多,然而通过合理安排开关序列,电流波形质量可以和主动控制下的相同。因此,与不加控制及主动控制策略相比,所提出的精细分区控制策略不但可明显改善中点电位平衡效果,还可维持输出电流波形质量较高。 为了验证精细分区控制策略对不同基波频率的有效性,图12为调制度m=0.85时,载波频率fs不变,基波频率f为10 Hz的实验波形。 图12 基波频率f=10 Hz时的实验波形 对比图12a与图8c、图12b与图10c可看出,由于基波频率降低,载波频率保持不变,每个基波周期内参与合成的PWM周期数增大1倍,中点电位更易平衡,精细分区控制策略对电容电压波动抑制效果更好,输出线电压波形更为平整。 本文针对低开关频率下NPC三电平逆变器中点电位波动问题,通过分析中点电流与中点电位波动的关系,并考虑舍弃冗余状态对工作区域划分的影响,提出了一种精细分区控制中点电位平衡的新方法。该方法在低调制度下对占空比分配因子进行限幅,尽量控制中点电流为零;在高调制度下,将最值电流法和分配因子法相结合,将工作区域精细划分为CI、UI和DI三个区域,并针对不同工作区域,采用不同调制方法尽量控制中点电流绝对值最小,从而控制中点电位平衡。仿真和实验结果表明,所提出的精细分区控制策略所使用的开关频率较低,中点电位平衡效果较优,输出负载电流波形质量较高,因而适用于牵引系统等要求低开关频率、高运行品质的场合。 [1] 张紫凡.CRH2型动车组牵引变流器的建模仿真与控制策略研究[D].北京:华北电力大学,2013. [2] Rodriguez J,Bernet S,Steimer P K,et al.A survey on neutral-point-clamped inverters[J].IEEE Transactions on Industrial Electronics,2010,57(7):2219-2230. [3] 王兆宇,艾芊.三电平逆变器空间矢量调制及中点电压控制[J].电力系统保护与控制,2011,39(20):131-136. Wang Zhaoyu,Ai Qian.Space vector modulation for three-level inverter and neutral point potential control[J].Power System Protection and Control,2011,39(20):131-136. [4] Pou J,Pindado R,Boroyevich D,et al.Evaluation of the low-frequency neutral-point voltage oscillations in the three-level inverter[J].IEEE Transactions on Industrial Electronics,2005,52(6):1582-1588. [5] 姜卫东,王群京,史晓锋,等.中点箝位型三电平逆变器在空间矢量调制时中点电位的低频振荡[J].中国电机工程学报,2009,29(3):49-55. Jiang Weidong,Wang Qunjing,Shi Xiaofeng,et al.Low frequency oscillation of neutral point voltage of neutral-point-clamped three-level VSI under SVPWM control[J].Proceedings of the CSEE,2009,29(3):49-55. [6] Beig A R,Narayanan G,Ranganathan V T.Modified SVPWM algorithm for three level VSI with synchronized and symmetrical waveforms[J].IEEE Transactions on Industrial Electronics,2007,54(1):486-494. [7] 谢路耀,金新民,吴学智,等.基于零序注入的NPC三电平变流器中点电位反馈控制[J].电工技术学报,2012,27(12):117-128. Xie Luyao,Jin Xinmin,Wu Xuezhi,et al.Neutral point voltage feedback control based on zero sequence injection for NPC three-level converter[J].Transactions of China Electrotechnical Society,2012,27(12):117-128. [8] 张伦健,谭国俊,陈利萍.基于双调制波技术的三电平Z源逆变器中点电位平衡控制[J].电力系统保护与控制,2013,41(7):91-96. Zhang Lunjian,Tan Guojun,Chen Liping.Neutral-point potential balance control for three-level Z-source inverters based on double modulation wave technique[J].Power System Protection and Control,2013,41(7):91-96. [9] Zhang J,Yokoyama R,She J.Neutral-point voltage control for a three-level DC-AC inverter using equivalent-input-disturbance approach[J].Power System Protection and Control,2013,41(1):183-189. [10]孟庆云,马伟明,孙驰,等.考虑二极管非理想特性的中点钳位三电平电路的分析[J].电工技术学报,2010,25(6):40-46,54. Meng Qingyun,Ma Weiming,Sun Chi,et al.The NPC three-level circuit considering nonideal characteristic of diode[J].Transactions of China Electrotechnical Society,2010,25(6):40-46,54. [11]Shen J,Schroder S,Rosner R,et al.A comprehensive study of neutral-point self-balancing effect in neutral-point-clamped three-level inverters[J].IEEE Transactions on Power Electronics,2011,26(11):3084-3095. [12]Xia C,Shao H,Zhang Y,et al.Adjustable proportional hybrid SVPWM strategy for neutral-point-clamped three-level inverters[J].IEEE Transactions on Industrial Electronics,2013,60(10):4234-4242. [13]Jiao Yang,Lee F C,Lu Sizhao.Space vector modulation for 3-level NPC converter with neutral voltage balancing and switching loss/noise reduction[C].Twenty-Ninth Annual IEEE Applied Power Electronics Conference and Exposition (APEC),Fort Worth,TX,2014:1780-1787. [14]周京华,贾斌,章小卫,等.混合式三电平中点电位平衡控制策略[J].中国电机工程学报,2013,33(24):82-89. Zhou Jinghua,Jia Bin,Zhang Xiaowei,et al.A hybrid three-level neutral-point balance control strategy[J].Proceedings of the CSEE,2013,33(24):82-89. [15]Orfanoudakis G I,Yuratich M A,Sharkh S M.Nearest-vector modulation strategies with minimum amplitude of low-frequency neutral-point voltage oscillations for the neutral-point-clamped converter[J].IEEE Transactions on Power Electronics,2013,28(10):4485-4499. [16]张志,谢运祥,乐江源,等.消除中点电位低频振荡的三电平逆变器空间矢量脉宽调制方法[J].电工技术学报,2011,26(3):103-109. Zhang Zhi,Xie Yunxiang,Le Jiangyuan,et al.SVPWM method of removing the low-frequency oscillations of neutral point voltage for three-level NPC inverter[J].Transactions of China Electrotechnical Society,2011,26(3):103-109. Neutral Point Potential Balance Strategy for NPC Three-level Inverter Based on Meticulous Partition Control WangHuimin1WenKunpeng1ZhangYun2XiaChangliang1,2 (1. Tianjin Key Laboratory of Advanced Electrical Engineering and Energy TechnologyTianjin Polytechnic University Tianjin 300387 China 2.School of Electrical Engineering and Automation Tianjin University Tianjin 300072 China) To solve the problem of neutral point potential fluctuation of neutral point clamped (NPC) three-level inverter,a meticulous partition control strategy is proposed based on the three vectors and four states synthetic method.In the low modulation degree,the amplitude of the duty cycle distribution factor is limited in order to eliminate the neutral point current.In the high modulation degree,through analyzing the judgment difference between extreme current value method and distribution factor method,the working area is divided to controllable interval (CI),uncontrollable interval (UI),and doubtful interval (DI).The adscription of DI is analyzed based on the control effect of the neutral point current,which minimize the neutral point current without increasing the operating frequency.By these,the neutral point potential fluctuation can be decreased with a low switching frequency,which is verified by the results of the simulations and experiments. NPC three-level inverter,neutral point potential balance,three vectors and four states modulation,meticulous partition control 国家自然科学基金(51207104)和天津市高等学校科技发展基金计划项目(20140414)资助。 2015-01-09 改稿日期2015-08-02 TM464 王慧敏 女,1983年生,博士,讲师,研究方向为电机系统及其控制。(通信作者) 温坤鹏 男,1989年生,硕士研究生,研究方向为电机系统及其控制。
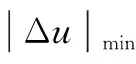

3 实验研究





4 结论

