磁谐振式无线电能传输系统谐振器参数对传输性能的影响性分析

王 维 黄学良 谭林林 赵俊峰 陈 琛

(1.东南大学电气工程学院 南京 210096 2.江苏省智能电网技术与装备重点实验室 镇江 212000)



磁谐振式无线电能传输系统谐振器参数对传输性能的影响性分析

王 维1，2黄学良1，2谭林林1，2赵俊峰1，2陈 琛1，2

(1.东南大学电气工程学院 南京 210096 2.江苏省智能电网技术与装备重点实验室 镇江 212000)

针对磁谐振式无线电能传输系统进行设计，需要在不同场合下挖掘其最优化传输性能。通过对磁谐振式无线电能传输系统特别是目前常用的含中继谐振器的四线圈无线电能传输系统进行相应的理论建模分析，采用参数归一化解析理论，探讨最优化传输效率及最大化输出功率的影响因素以及在设计过程中两种实现目标的内在关系。通过理论仿真及实验验证的方式得出在系统工作频率确定的前提下，磁谐振式无线电能传输系统最优化传输效率以及最大化输出功率一定不拟合。将理论结果应用到无线电能传输系统的设计中，发现在系统设计条件不变的前提下，存在确定匝数及半径的能量接收线圈可使得系统传输效率或输出功率达到最优化。

无线电能传输 磁谐振 传输性能 参数归一 最优化

0 引言

无线电能传输技术是美籍克罗地亚裔物理学家Nikola Tesla于19世纪提出并进行了研究[1]，由于早期的技术因素限制，该技术仅局限于设想阶段，未能成功实施。经过一百多年的研究过程，无线电能传输技术(Wireless Power Transmission，WPT)已逐渐成熟，并在各领域内都走向了实用化的道路。无线电能传输系统按照功率等级可分为小功率无线充电系统及kW级无线供电系统两大类。小功率无线充电系统涉及面较为广泛，从便民家电到植入医疗均有不同程度的应用[2-4]，且前景广阔。kW级无线供电系统在目前的市场前沿探究中主要涉及到电动汽车无线充电[5，6]这一战略性领域，这是化石能量面临枯竭而必须要跨出的重要一步。

无线电能传输技术从传输方式上可分为短程无线传输与中远程无线传输两大类。短程无线电能传输技术以电磁感应式为代表，而中远程无线电能传输技术则以磁耦合谐振方式为代表，在目前研究中最为广泛[7]。谐振器是影响无线电能传输系统传输特性的重要因素，国内外研究学者分别从磁场特性[8]、功耗特性[9]和耦合能力[10]等方面对平面螺旋谐振器进行综合分析及优化设计。然而对于空间螺旋谐振器参数对无线电能传输系统性能的影响却研究很少，这对于该项技术的发展非常不利。

本文对含中继谐振器的四线圈无线电能传输系统[11]进行相应的理论建模及特性分析，采用参数归一化解析理论，从电路本质上探讨最优化传输效率和最大化输出功率的实现方式以及在设计过程中两种实现目标的内在关系。同时，将理论结果应用到实际系统设计中，探讨在系统其他参数不变的前提下，接收谐振器的匝数、半径变化是否与系统最优化传输效率或输出功率之间存在对应关系，从而在不同优化目标下的实际系统中，指导能量接收线圈进行优化设计。

1 系统理论建模与分析

目前，针对无中继的无线电能传输系统，能量发射端与接收端可采取串联补偿谐振或并联补偿谐振，因此无线电能传输系统的模型建立可分为4种：串串(SS)、串并(SP)、并串(PS)、并并(PP)[12，13]。然而，本质上任何含中继谐振器的系统在分析建模时均可通过等效电路将参数归算至发射与接收线圈两侧进行分析。而本文主要针对实际应用系统中采用较多的电压源输入式四线圈串联谐振结构进行建模分析，且分析方法适用于所有结构形式的无线电能传输系统。从电路本质上来说，在接入负载确定的情况下，无线电能传输系统的输出功率Pout仅与负载侧流入的电流Il有关，即

(1)

而系统的传输效率仅与能量传输与接收线圈中的储能比有关，即

(2)

式中Lt、Lr分别为能量传输与接收线圈的自身电感值。同时，能量传输与接收线圈中的谐振电流存在一定的比例关系，假定比例系数为k，且k为与电路其他参数有关的复系数，则可令

Ir=kIt

(3)

故式(2)可化简为

(4)

从式(4)中可明显看出，当电路其他参数都确定后，系统传输效率仅与能量传输和接收线圈的自感比值有关，为了能更准确地分析系统输出功率与传输效率之间的关系，本文在以上理论的基础上将对电压源输入式四线圈串联谐振无线电能传输系统进行建模分析，找出两者之间的内在联系。其中，物理模型如图1所示，等效电路模型如图2所示。

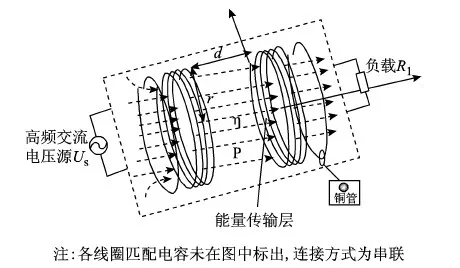
图1 系统物理模型图

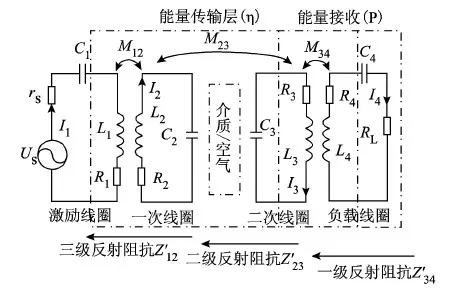
图2 系统电路模型图

图1、图2所示模型图中，从左至右依次包含高频交流电压源Us、激励线圈L1、能量发射线圈L2、能量接收线圈L3、负载线圈L4、负载R1。图1中各线圈匹配电容未在图中标出，其与线圈连接方式均为串联方式。谐振器在高频环境下存在趋肤效应，为了减少由此带来的功率损耗影响，本文所设计的谐振器材质都采用空心冷轧铜管。

对于空心螺旋线圈之间的互感系数，数学家Neumann给出了合适的计算公式，经过化简后为

(5)

式中：μ0为磁常数；N1、N2分别为两线圈的匝数；d为两线圈的轴向距离；θ、φ均为积分因子。为了简化分析过程，本文中所涉及的线圈半径均相等且为r。文献[14]验证了该公式在无线电能传输系统线圈互感求解的正确性。表明当传输距离大于最小限定距离dmin后，对于图2所示电路模型，可忽略激励线圈与能量接收线圈、负载线圈的互感M13和M14以及能量发射线圈与负载线圈的互感M24，故在对系统进行电路建模解析时，只需考虑互感因素M12、M23、M34。

针对图2给出的系统电路模型图，可列出系统能量传输过程中的等效KVL方程式中：Z1、Z2、Z3、Z4均为各谐振回路的自阻抗，Z1=R1+jωL1+1/(jωC1)，Z2=R2+jωL2+1/(jωC2)，Z3=R3+jωL3+1/(jωC3)，Z4=R4+jωL4+1/(jωC4)。 在系统设计时，为减少电路无功损耗，均使得线圈处于谐振状态，即

(6)

jωLn+1/(jωCn)=0n=1,2,3,4

(7)

由式(6)可进一步推算出

(8)式中：k1=rs+R1；k2=R4+RL。 从式(8)的理论推导中可见，系统的传输效率由谐振器的自感与互感共同决定，而输出功率仅与其互感有关。故在实际系统的设计中需根据优化目标的不同而选择需要调整的具体参数。

同时，为了进一步分析谐振器参数对其系统传输性能的影响，本文采用参数归一化解析理论，将系统传输效率及负载接收功率的优化归算至谐振线圈L3的匝数Nr以及线圈半径r的设计中，探讨其参数设计对系统性能的影响。文献[15，16]分别给出了空心螺旋电感以及螺旋线圈损耗电阻的近似计算公式

(9)

(10)

式中：L为电感量，μH；μ0为真空中的磁导率；N为线圈匝数；S为螺旋线圈的横截面积，m2；l为螺旋线圈轴向长度，m；k为与2r/l有关的量化系数；r为线圈的径向半径，m；R为铜管的有效截面积半径，cm；σ为导体电导率，S/m。对于设计变量Nr与r对系统传输性能的影响分析，本文采用分别归一化处理的方式对其进行讨论。

1)取谐振器匝数Nr为基本设计变量。

由式(9)可看出线圈自身电感Lr随匝数Nr的增加呈非线性增长趋势，而线圈间的互感参数则与Nr呈单调关系。通过推导，可得系统传输性能与线圈匝数Nr存在以下关系

(11)

(12)

式中：当系统其他参数均确定时，a1、a2、b1、b2、c1、c1分别为包含系统其余参数的定系数；k为随Nr增加的非线性增长系数。故随着Nr的增加，η在一定范围内存在相应的最大值，而Po则一直呈增长趋势，没有极值点。

2) 取谐振线圈半径r为基本设计变量。

谐振线圈的半径是影响线圈自身电感及线圈间互感的重要参数。但从式(5)和式(9)可以看出，半径r被包含在复杂的运算中。为了能更加清晰明了地反映出r与系统传输性能之间的关系，本文采用仿真模拟与实验对比的方法对其进行分析。

2 传输性能的仿真分析

对于本文所设计的磁谐振式无线电能传输系统，为了更准确、形象地分析其传输效率及输出功率与中继线圈匝数和半径之间的关系，本文采用电磁仿真软件及数值计算软件相结合的方式对系统进行仿真分析，在可接受误差范围内验证上述分析的正确性，同时在传输距离一定的情况下对系统参数进行优化设计，达到最优化传输效率或输出功率的设计目标。

仿真中的系统参数如表1所示，每组线圈均通过匹配电容使之在工作频率(本文设为3 MHz)下发生谐振，同时采用模拟恒压源(内阻rs=50 Ω)作为激励源，传输距离设定为30 cm，负载选用50 Ω纯阻性负载，以便在分析中得到更加切合实际的结果。

表1 磁耦合谐振式无线电能传输系统仿真参数

1)为了研究系统传输效率、负载接收功率与能量接收线圈匝数之间的关系，在仿真中，取能量接收线圈的半径与其他线圈一致，即r=15 cm，以发射与接收线圈间的磁场交互强度描述系统的传输效率，并同时计算得出相应的负载功率，仿真分析如图3所示。

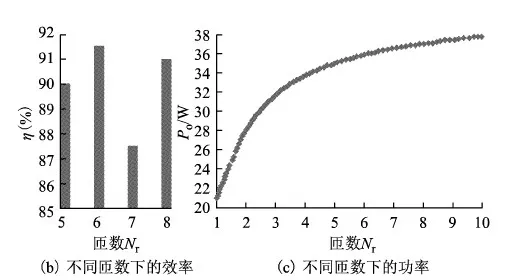
图3 系统传输性能与谐振器匝数的关系图

如图3所示，在含中继线圈的磁耦合谐振式无线电能传输系统其他条件均一致的条件下，系统传输效率在接收中继线圈匝数的有效设计范围内存在最优值(本文设计系统中最优化匝数设计为Nr=6)，而负载的接收功率却随接收中继线圈匝数的增加而呈逐渐递增趋势。这是因为系统传输效率仅与中继线圈内的电流大小及线圈自身电感有关，负载接收功率仅与负载线圈内的电流大小有关，当线圈匝数增加时，线圈的自身内阻及线圈间的互感呈线性增加，而线圈的自身电感呈非线性增长，这些因素综合起来使得中继线圈内的电流呈非线性增长趋势，导致负载线圈中的电流也呈非线性增长，负载功率非线性增加。而当系统达到传输效率最优化时，能量接收中继线圈中的电流并非是最大值。这也从另一方面验证了理论分析的正确性。

2)为了研究系统传输效率、负载接收功率与能量接收线圈半径之间的关系，在仿真中，取能量接收线圈的匝数为传输效率最优化匝数，即Nr=6，同样以发射与接收线圈间的磁场交互强度描述系统的传输效率，并同时计算得出相应的负载功率，仿真分析如图4所示。

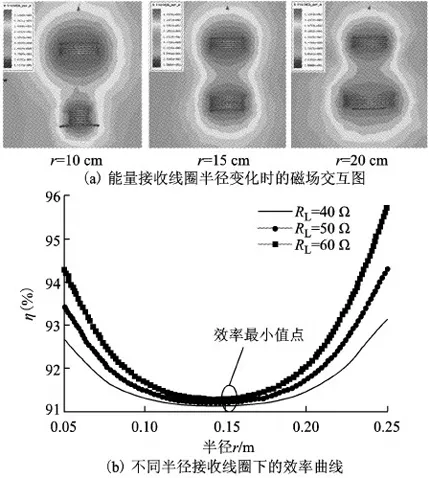
图4 系统传输性能与接收线圈半径关系图

由图4可清晰地看出，当系统能量接收线圈匝数不变的前提下，系统传输效率最小值点出现在接收线圈半径与其他线圈半径相同时，在本文设计的系统中即rL3=15 cm。针对不同负载的接入，系统传输效率略有变化，但出现传输效率最小值点的位置不变。负载接收功率与传输效率的曲线截然不同，当负载值变化不大时，其接收功率最大值点出现在略大于15 cm处。这也从另一方面说明了当线圈处于最优化效率匝数时，线圈半径对系统传输效率的影响不大，但对负载接收功率的影响很大，这主要是因为线圈半径变化导致了线圈间互感发生变化，系统反射阻抗也发生变化，最终影响了最大输出功率出现时的阻抗匹配点。实际设计过程中可根据不同负载的接入略微增加或减小接收线圈的半径来达到最大功率输出。

3 传输性能的实验验证

为了验证理论与仿真分析的正确性，本文对相关理论结论进行了较为精确的实验验证。相关实验参数同仿真一致，见表1。实验装置如图5所示，图中标示的①、②、③、④为各线圈端的调谐电容。实验中负载均取RL=50 Ω的灯泡，实验结果如图6所示。

由图6可明显看出，当系统其他参数一定的条件下，系统传输效率随匝数增加而呈非线性变化，且存在最大值，本文设计的系统效率最大值点位Nr=6，而系统输出功率则随匝数的线性增加呈缓慢增长趋势。对于能量接收线圈的半径对系统传输性能的影响，图6中可看出，当接收线圈半径与其他线圈相同时，系统传输效率最低；在半径有限变化范围内，系统传输效率略有提高，但幅度不大。系统输出功率随半径增加也略有提高，这主要归因于系统的阻抗匹配，与理论与仿真分析基本一致。

图5 实验装置图

图6 系统传输性能随匝数/半径变化图

4 结论

本文通过对磁谐振式无线电能传输系统进行建模分析，采用参数归一化解析理论，探讨最优化传输效率和最大化输出功率的实现方式，以及分析谐振线圈匝数和半径大小与这两种实现目标的内在关系。由理论分析与实验验证可以得出，在实际系统的设计过程中，可根据以下方法实现设计中所追求的传输性能：①通过增加线圈匝数可单方面提高负载接收功率；②选择最优化线圈匝数及采用半径略大或略小于其他线圈的接收谐振器可提高系统传输效率；③选择最优化线圈匝数及采用半径略大于其他线圈的接收谐振器可综合提高系统总体传输性能。以上结论对磁谐振式无线电能传输系统的实用化设计奠定了良好的理论基础。

[1] 黄学良，谭林林，陈中，等.无线电能传输技术研究与应用综述[J].电工技术学报，2013，28(10)：1-11. Huang Xueliang，Tan Linlin，Chen Zhong，et al.Review and research progress on wireless power transfer technology[J].Transactions of China Electrotechnical Society，2013，28(10)：1-11.

[2] 张剑韬，朱春波，陈清泉.应用于无尾家电的非接触式无线能量传输技术[J].电工技术学报，2014，29(9)：33-37. Zhang Jiantao，Zhu Chunbo，Chen Qingquan.Contactless wireless energy transfer technology applied to tail-free household appliances[J].Transactions of China Electrotechnical Society，2014，29(9)：33-37.

[3] 赵军，杨新生，徐桂芝，等.Witricity 系统对作用于人体胸腔电磁环境的研究[J].电工技术学报，2013，28(S2)：200-203. Zhao Jun，Yang Xinsheng，Xu Guizhi，et al.Research on electromagnetic environment to chest via witricity[J].Transactions of China Electrotechnical Society，2013，28(S2)：200-203.

[4] Ahn D，Hong S.Wireless power transmission with self-regulated output voltage for biomedical implant[J].IEEE Transactions on Industrial Electronics，2014，61(5)：2225-2235.

[5] Onar O C，Miller J M，Campbell S L，et al.A novel wireless power transfer for in-motion EV/PHEV charging[C].2013 Twenty-Eighth Annual IEEE Applied Power Electronics Conference and Exposition (APEC) Long Beach，CA，2013：3073-3080.

[6] Shin J，Shin S，Kim Y，et al.Design and implementation of shaped magnetic-resonance-based wireless power transfer system for roadway-powered moving electric vehicles[J].IEEE Transactions on Industrial Electronics，2014，61(3)：1179-1192.

[7] Liu C，Chau K T，Zhang Z，et al.Multiple-receptor wireless power transfer for magnetic sensors charging on Mars via magnetic resonant coupling[J].Journal of Applied Physics，2015，117(17)：17A743.

[8] Zhang X，Ho S L，Fu W N.Quantitative analysis of a wireless power transfer cell with planar spiral structures[J].IEEE Transactions on Magnetics，2011，47(10)：3200-3203.

[9] Wang J，Li J，Ho S L，et al.Study and experimental verification of a rectangular printed-circuit-board wireless transfer system for low power devices[J].IEEE Transactions on Magnetics，2012，48(11)：3013-3016.

[10]Fotopoulou K，Flynn B W.Wireless power transfer in loosely coupled links：coil misalignment model[J].IEEE Transactions on Magnetics，2011，47(2)：416-430.

[11]王维，黄学良，周亚龙，等.双中继无线电能传输系统建模及传输效率分析[J].电工技术学报，2014，29(9)：1-6. Wang Wei，Huang Xueliang，Zhou Yalong，et al.Modeling and transmission efficiency analysis of wireless power transmission system with dual relays[J].Transactions of China Electrotechnical Society，2014，29(9)：1-6.

[12]Chen Linhui，Liu Shuo，Zhou Yongchun，et al.An optimizable circuit structure for high-efficiency wireless power transfer[J].IEEE Transactions on Industrial Electronics，2013，60(1)：339-349.

[13]黄学良，吉青晶，谭林林，等.磁耦合谐振式无线电能传输系统串并式模型研究[J].电工技术学报，2013，28(3)：171-176. Huang Xueliang，Ji Qingjing，Tan Linlin，et al.Study on series-parallel model of wireless power transfer via magnetic resonance coupling[J].Transactions of China Electrotechnical Society，2013，28(3)：171-176.

[14]Huang X L，Wang W，Tan L L，et al.Study of transmission performance on strong coupling wireless power transfer system in free position[C].Session 2P4 Near to Mid-range Wireless Power Transfer Technology：Principles and Applications 2，Moscow，2012：383.

[15]П·Л·卡兰塔罗夫，Л·А·采伊特林.电感计算手册[M].陈汤铭，刘保安，罗应立，等译.北京：机械工业出版社，1992.

[16]黄辉，黄学良，谭林林，等.基于磁场谐振耦合的无线电力传输发射及接收装置的研究[J].电工电能新技术，2011，30(1)：32-35. Huang Hui，Huang Xueliang，Tan Linlin，et al.Research on transmitter and receiver of wireless power transmission based on magnetic resonance coupling[J].Advanced Technology of Electrical Engineering and Energy，2011，30(1)：32-35.

Effect Analysis Between Resonator Parameters and Transmission Performance of Magnetic Coupling Resonant Wireless Power Transmission System

WangWei1,2HuangXueliang1,2TanLinlin1,2ZhaoJunfeng1,2ChenChen1,2

(1.School of Electrical Engineering Southeast University Nanjing 210096 China 2.Key Laboratory of Jiangsu Province Smart Grid Technology with Equipment Zhenjiang 212000 China)

When designing a magnetic coupling resonant wireless power transmission system，we need to seek optimal transmission performance under different situations.By modeling analysis for the magnetic coupling resonant wireless power transmission system，especially the four-coil-system with dual relays, we use normalized parameter analytical theory to explore the way of realizing optimal transmission efficiency and output power，as well as the internal relations between these two targets.By theoretical simulations and experiments，the optimal transmission efficiency and the optimal output power are not matching when the system operating frequency is determined.Ultimately，applying the theory results to the design of actual system，it is found that there are determined turns or radius of receiving coils which can provide maximum transmission efficiency or output power when other parameters of the system is unchanged.

Wireless power transmission，magnetic coupling resonant，transmission performance，parameters normalized，optimization

国家自然科学基金(51177011)和江苏省普通高校研究生科研创新计划(KYLX15_0133)资助项目。

2015-05-28 改稿日期2015-06-16

TM12；TM133

王 维 男，1988年生，博士研究生，研究方向为无线电能传输技术。

黄学良 男，1969年生，教授，博士生导师，研究方向为无线电能传输技术、新型能源转换装置研究和智能用电技术等。(通信作者)