双谐振耦合能量信息同步传输技术研究

郭 尧 魏 国 郝潇潇 朱春波

(哈尔滨工业大学 哈尔滨 150001)



双谐振耦合能量信息同步传输技术研究

郭 尧 魏 国 郝潇潇 朱春波

(哈尔滨工业大学 哈尔滨 150001)

无线电能传输技术实现了对设备的非接触供电，适应了特殊场合(如移动设备和旋转设备)供电需求，避免了传统传导式供电带来的诸多问题。然而在实际应用中(如医学电子胶囊、无线供电时的信息反馈等)，在能量无线传输的同时还要求信息的同步传输。针对这类应用，提出一种新型双谐振结构，利用其固有的双谐振特性，在一对线圈中实现能量和信号的同步传输。在分析双谐振电路特性的基础上，通过提出传输因子的概念，分析其信道带宽与响应时间，并研究传输因子与能量/信息传输性能的关系。实验表明，当负载小于10 Ω，传输距离小于120 mm时，能量传输效率高于70%。通过开关键控调制方式，在负载值1.31 Ω、距离122 mm时，实现了50 kHz的有效传输。

双谐振耦合 无线 电能传输 信息传输

0 引言

自美国麻省理工学院的Marin Soljacic教授等于2006年11月在美国AIP工业物理论坛上首次提出磁耦合谐振无线电能传输技术的概念[1]以来，该技术快速发展，并逐渐应用到手机、家用电器、电动汽车及轨道交通等诸多领域。

在研究磁耦合谐振技术用于能量传输的同时，国际上一些机构开始着手研究该技术用于通信领域。如乔治亚理工学院Z.Sun等[2]研究了土壤中磁通信的通道损耗、误码率和带宽等问题，提出用LC无源中继增加通信距离的方法；美国阿拉巴马大学S.Bae等[3]研制了基于磁通信的矿难应急通信装置，工作频率48 kHz，实现地下1 km语音通信。

磁通信与磁耦合能量传输在理论模型上几乎相同，只是在电路工作状态上有所不同。由于其具有的诸多优点，部分学者开始针对特殊应用场合下的能量信号同步传输进行研究。文献[4]提出一种DCSK调制方法，使电能传输功率改变时不影响数据传输，但该文中所提出的结构要求二次侧有两个接收线圈：一个用于接收数据，一个用于能量接收和时钟同步，增加了系统复杂程度。文献[5]研究了在谐振式无线电能系统中使用频分复用(OFDM)技术的单向信息同步传输方式，其信息与能量共用耦合机构，传输距离10 cm，然而这种基于电能传输通道的同步信息传输方法无法兼顾带宽与效率(虽然较小的Q值可获得较大的通信带宽，但也导致能量传输效率较低)。文献[6，7]提出一种用于引信的能量和信息非接触同步传输技术。文献[8]提出了基于电能通道的数字信号双向传输方法。文献[9]通过在逆变源前加入Boost调制环节，实现能量信息同步传输。

为了解决利用能量通道传输信息的诸多缺陷，保证能量传输的连续性和信息传输速率，本文提出一种新型双谐振结构，利用其固有的双谐振特性，分别进行能量和信息的传输。首先分析了双谐振电路的特性，然后分析了其信道带宽与响应时间，并研究了传输因子与能量/信息传输性能的关系，最后搭建了实验平台，研究了不同距离、负载下能量传输特性及通信速率对信号传输的影响。

1 双谐振电路分析

1.1 谐振频率分析

双谐振电路结构如图1所示，由串联的电感L和电容C及并联的电感La和电容Ca组成，其总阻抗为

(1)

其阻抗谱如图2所示，可看到电路存在两个串联谐振点f1、f2以及一个阻抗无穷大的并联谐振点f3。因为本文中激励源为电压源，因此仅采用f1和f2作为电路的两个谐振频率，在谐振频率处电路总阻抗最小，呈纯阻性。

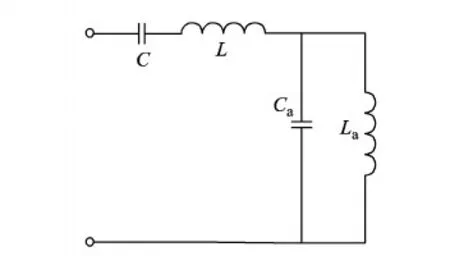
图1 双谐振电路

图2 双谐振电路总阻抗与频率关系

f1和f2对应的角频率为

(2)

下面分析L与C、La及Ca的取值和ω0、ωa、ω1、ω2的关系。

当L=xLa，C=yCa， 且x>1，xy>1， 也即L>La且ω0<ωa时，有ω1=αω0，ω2=βωa， 其中α、β表明了ω1、ω2相对于ω0、ωa的偏移程度，且

(3)

此时α<1，β>1，且随着x、y的增大，α、β均趋近于1，如图3所示。此外，α与β的变化受电感倍数x的影响较为明显，各频率间的关系为ω1<ω0<ωa<ω2。

图3 偏移量α与β随x、y的变化趋势

另一种情况，当La=xL，Ca=yC且x>1，xy>1， 也即Lωa时，有ω1=αωa，ω2=βω0， 其中

(4)

此时α与β的总体变化趋势与前面相同，但其变化受y的影响更为明显，并且与电感倍数x基本无关，如图4所示，各频率间的关系为ω1<ωa<ω0<ω2。

图4 第二种情况下α与β变化趋势

1.2 等效电感与传输因子的提出

无论是无线电能传输还是信息传输，其传输特性均与品质因数Q密切相关。而在双谐振电路中，其品质因数计算较为复杂，因此需要找到一个更为合适的参数用于衡量能量/信息的传输。

设电压源US=UScosωt激励下电路各部分电流如图5所示。

图5 电压源激励下各部分电流

电路工作于谐振频率ω1时，电感电流与电容电压瞬时值为

(5)

(6)

(7)

(8)

电路储能为

(9)

对式(9)求导，可解出在ω1t=0和ω1t=π/2时刻为储能的极值点，分别记为W储1和W储2

(10)

(11)

对求得的两个储能做差，其结果如图6所示，可以看到两储能之差近似为零，可认为两种表达式基本相等，都能表示储能最大值。

图6 两个储能值之差

一个周期内消耗的能量就是电阻所产生的热损耗

(12)

根据品质因数的定义

并带入式(10)和式(12)，则双谐振电路的品质因数为

(13)

同理，当电路工作于谐振频率ω2时

(14)

(15)

同时，由式(5)与式(7)可得

(16)

式中λ为并联电感电流与串联电感电流之比，λ同样出现在等效电感与品质因数的表达式中，并且在后续分析中与能量和信号的传输性能相关，本文中将其称作传输因子。

1.3 耦合电感的选择

由于双谐振电路中存在两个电感，而无线能量/信息的传输需要一、二次侧的互感耦合，因此本节将通过进一步分析，选择合适的电感作为发射/接收线圈。

首先当L=xLa，C=yCa， 且x>1，xy>1时，传输因子随x、y变化曲线如图7所示。可以看到，低频ω1时传输因子λ接近于1，电感L和La中的电流几乎相等。高频ω2时传输因子随x的增加而增大，即等效电感增大，导致带宽变窄，响应时间变长。

当La=xL，Ca=yC， 且x>1，xy>1时，传输因子随x、y的变化曲线如图8所示。可以看到，低频ω1时λ随y的增加而增大，而较大的传输因子意味着并联电感的电流大于串联电感电流，具有电流放大作用。高频ω2时在整个x、y变化区间λ一直较小，这意味着此时的带宽较宽，响应时间较短。

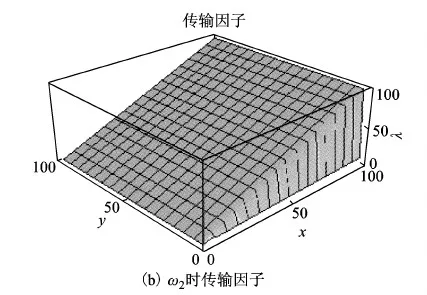
图7 传输因子随x、y变化曲线

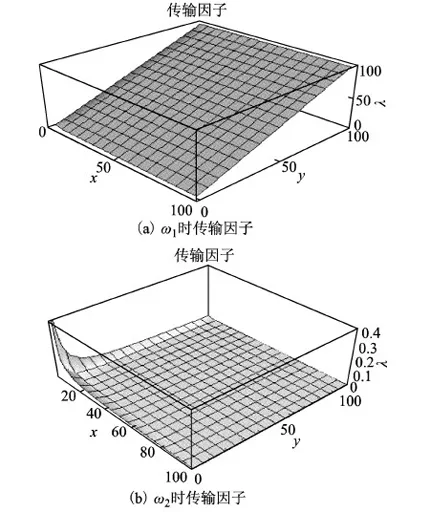
图8 第二种情况下传输因子随x、y变化曲线

因此选择并联电感作为耦合线圈，且并联电感值大于串联电感值，ωa<ω0，这样低频时线圈上具有较大的电流，增强能量传输能力，而高频时具有较高的带宽和较短的响应时间，保证通信速率。此时各频率关系为ω1<ωa<ω0<ω2。

2 双谐振耦合建模分析与参数选择

采用并联电感作为互感耦合的电路模型如图9所示，L1、C1和L2、C2分别为一、二次侧串联电感电容；La1、Ca1和La2、Ca2分别为一、二次侧并联电感电容。RS为交流电压源内阻，RL为负载电阻。

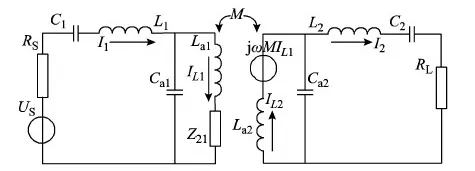
图9 双谐振电路互感耦合模型

电路的各部分阻抗为

(17)

式中：Z2(ω)为二次侧的总阻抗；Z21(ω)为二次侧到一次侧的反映阻抗；Z1(ω)为一次侧的总阻抗。

可求得电路中各电感电流和负载电压为

(18)

从而输入和输出电压的关系为

URL(ω)=G(ω)US

(19)

负载所接收到的功率为

(20)

则能量传输效率为

(21)

采用数学软件对参数赋值后，就可以进行绘图观察。

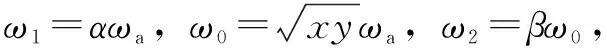
(22)

传输因子与电感电容的选择密切相关，这些参数的选择关系到整个系统的传输性能。

对于能量传输，选择较低的频率可以降低辐射和线圈上的趋肤效应，逆变电路及其控制也更容易实现，而对于信息传输，为了获得较高的通信速率，需要较高频率的载波。因此在设计中，我们希望ω1和ω2的频率差尽可能大，有两种方法：

方法一：使ω1接近ωa，ω0接近ω2，且增大ωa与ω0的频率差。此时xy较大，且α与β接近于1。由式(22)可知，用这种方法选择的参数，低频传输因子很大，高频传输因子很小。

方法二：使ω1尽量低于ωa，ω2尽量高于ω0，即令α较小而β较大。依据图4，要求xy>1时，y<1。用这种方法选择的参数，传输因子相对适中。

通过代入具体参数，对比两种参数选择方法。设低频f1为100 kHz附近，高频f2为900 kHz附近，RS=0.5 Ω，RL=20 Ω，US=10 V， 耦合系数k依次取值0.01、0.1、0.4。两种方法的电感电容取值如表1所示。

表1 各电感、电容参数取值

方法一计算的高频传输因子为0.017，低频传输因子为10.83；方法二计算的高频传输因子为0.113，低频传输因子为1.18。

对比图10和图11可知，低频时方法一较方法二更早地进入频率分叉，意味着低频时方法一具有更大的Q值(传输因子也更大)；对比图12和图13可知，高频时方法二传输功率更大，这是因为此时方法二的传输因子更大。

图10 方法一低频f1时的负载电压

图11 方法二低频f1时的负载电压

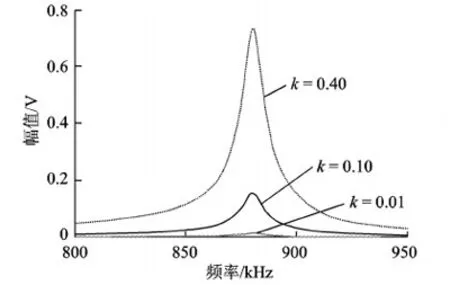
图12 方法一高频f2时的负载电压

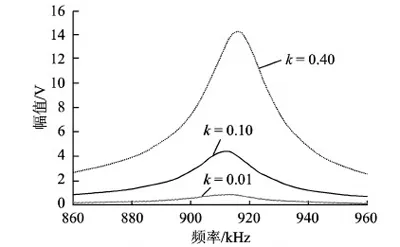
图13 方法二高频f2时的负载电压

将高频时两种方法的传输因子代入式(15)，分别为L+2.76×10-4La和L+0.0128La， 等效电感主要受串联电感的影响，而传输因子几乎不影响数据传输。

3 实验

实验电路相关参数如表2所示，为了保证信号传输的信噪比，采用方法二选取参数。逆变电路为全桥，信号调制方式为二进制开关键控，二次侧解调采用包络检波和比较整形。采用互感耦合的方式，通过串联电感将信号加入到双谐振电路中。考虑耦合电感对系统的影响，此时的低频谐振点为115.1kHz，高频谐振点为888kHz。

表2 实验参数选取

首先验证低频能量传输。传输距离为103 mm时，传输功率与效率随负载的变化如图14所示。

图14 传输功率与效率随负载变化曲线

随着负载的增加，系统的传输效率下降，负载值小于10 Ω时，传输效率大于70%。而负载值为20 Ω时达到匹配，传输功率最大。

选定负载电阻为2.96 Ω，测量距离从46 mm到266 mm(耦合系数从0.3到0.037变化)变化时的传输功率与效率。耦合系数较高出现频率分叉时，测量低频点的数据，结果如图15所示。

图15 传输功率与效率随距离变化曲线

随着距离增加，传输效率呈下降趋势。在距离为146 mm，耦合系数为0.074 4时达到阻抗匹配，传输功率最大。当传输距离小于120 mm时，传输功率与效率较为稳定。

然后验证高频信号传输。传输距离定为122 mm，负载为1.31 Ω，测得此时高频3 dB带宽为53 kHz，传输效率为4.92%。对于信号传输，效率不是主要的考虑因素，下面考察其传输速率。

在能量传输输入功率20 W的同时，一次侧发送频率为9.7 kHz交替的01信号，二次侧带通滤波及包络检波的波形如图16所示，原始信号与最后解调输出信号如图17所示。可看到经过带通后，信号较好地从能量中分离出来，且最终的解调输出与原始信号一致。将信号频率增至70 kHz，带通与包络检波的输出如图18所示。可看到此时信号的上升与下降边缘已经发生重叠，解调会产生较大的误码率，认为已经无法传输信号。经测量，二次侧带通输出信号的上升时间约为8 μs，而70 kHz的一个周期为14.3 μs，上升未完全响应就开始下降，所以电路的响应时间决定了最大通信速率。

图16 9.7 kHz带通与包络检波器输出波形

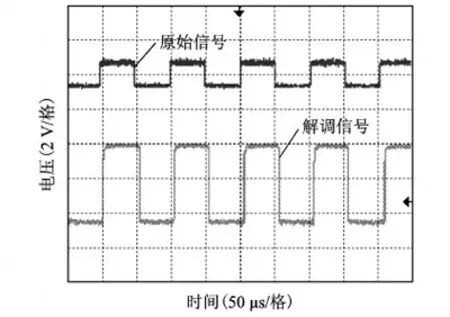
图17 9.7 kHz原始信号与解调信号

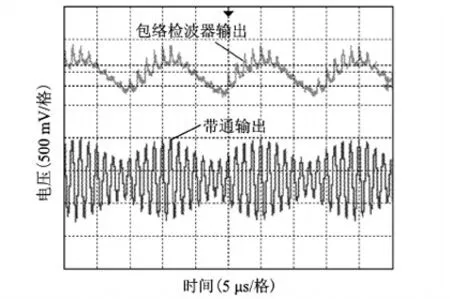
图18 70 kHz带通与包络检波器输出波形

实验达到的最大通信速率为50 kHz，原始信号与解调信号如图19所示。此时解调信号相对于原始信号存在一定延迟，这是由于受电路响应时间的影响。

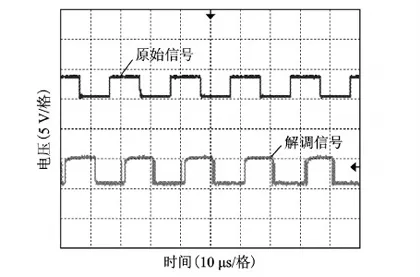
图19 50 kHz原始信号与解调信号

4 结论

本文提出一种新型双谐振结构，低频谐振点用于传能以降低辐射和趋肤效应，且使得逆变电路及控制更容易实现；高频谐振点用于通信以提高通信速率，解决传统的基于能量通道传输信号速率慢、能量传输不连续的问题。分析了双谐振电路的特性、耦合电感的选择、双谐振耦合模型和参数选择。

实验表明，当负载值小于10 Ω、传输距离小于120 mm时，可实现70%以上的能量传输效率。在负载为1.31 Ω，距离为122 mm时，可实现最高50 kHz的数据传输速率。

[1] Kurs A，Karalis A，Moffatt R，et al.Wireless power transfer via strongly coupled magnetic resonances[J].Science，2007，317(5834)：83-86.

[2] Sun Z，Akyildiz I F.Magnetic induction communications for wireless underground sensor networks[J].IEEE Transactions on Antennas and Propagation，2010，58(7)：2426-2435.

[3] Bae S，Hong Y K，Lee J，et al.Pulsed ferrite magnetic field generator for through-the-earth communication systems for disaster situation in mines[J].Journal of Magnetics，2013，18(1)：43-49.

[4] Mirbozorgi S A，Nejad M M.A novel data transfer technique for bio-implantable devices through the inductive power transfer link[J].Analog Integrated Circuits and Signal Processing，2013，74(2)：303-315.

[5] Noguchi S，Inamori M，Sanada Y.Reliable data transmission for resonant-type wireless power transfer[J].IEICE Transactions on Fundamentals of Electronics，Communications and Computer Sciences，2013，E96A(1)：298-303.

[6] 周晓东，张河.用于引信的电能和信息非接触同步传输技术[J].兵工学报，2003，24(3)：424-426. Zhou Xiaodong，Zhang He.Contactless synchronous transmission of power and information for fuzes[J].Acta Armamentarii，2003，24(3)：424-426.

[7] 李长生，张合.基于磁共振的引信用能量和信息无线同步传输方法研究[J].兵工学报，2011，32(5)：537-542. Li Changsheng，Zhang He.Research on wireless power and information synchronous transmission method based on magnetic resonance for fuzes[J].Acta Armamentarii，2011，32(5)：537-542.

[8] 刘洋.ICPT系统中信号双向传输机理研究[D].重庆：重庆大学，2013.

[9] 张爱国.感应式电能和信号同步传输技术的研究[D].哈尔滨：哈尔滨工业大学，2013.

Study on Wireless Power and Information Synchronous Transfer Based on Dual Resonant Coupling Circuits

GuoYaoWeiGuoHaoXiaoxiaoZhuChunbo

(Harbin Institute of Technology Harbin 150001 China)

Wireless power transfer (WPT) technology realizes contactless power supply to equipments，e.g. mobile devices and rotating machinery，and avoids problems caused by power supply wires.However，in practical applications, such as medical electronic capsule and information feedback in WPT，the synchronous transfer of information is required.For such applications，a new dual resonant circuit is proposed in this paper，which is able to realize the synchronous transmission of power and information.Based on the analysis of the dual resonant circuit，the concept of the transfer factor is proposed to analyze the channel bandwidth and response time.The relationship between the transfer factor and the energy/information transfer performance is also studied.Experiments show that the energy transfer efficiency is above 70% when load is less than 10 Ω and the distance is less than 120 mm.By using the on-off-keying modulation mode，50 kHz signal can be effectively transferred at 122 mm air gap with 1.31 Ω load.

Dual resonant coupling circuit，wireless power transfer，information transfer

国家自然科学基金(51277037)资助项目。

2015-05-28 改稿日期 2015-06-12

TM726.1

郭 尧 男，1987年生，博士研究生，研究方向为无线电能传输技术。

魏 国 男，1966年生，教授，研究方向为无线电能传输、现代敏感技术、信号处理。(通信作者)