首次积分法及其在非线性电报方程中的应用

李 钊，孙峪怀，黄 春

(四川师范大学数学与软件科学学院，四川 成都 610066)

首次积分法及其在非线性电报方程中的应用

李 钊，孙峪怀，黄 春

(四川师范大学数学与软件科学学院，四川 成都 610066)

在交换代数环理论的基础上，通过首次积分方法和Maple软件，研究了非线性电报方程，得到了该方程新的精确解.

首次积分法;非线性电报方程;精确解;除法定理

0 引言

非线性电报方程［1］，也称非线性传输方程，其形式为，

式中，α，β，γ，δ是常数，x代表空间位置，t表示时间，u表示某时刻各点的电位.

方程(1)是非常重要的数学物理方程，特别地，当α=1，β=0时，方程(1)为Klein-Gordon方程.因此求解方程(1)的精确解意义重大.对于方程(1)，范恩贵等［2］利用齐次平衡法并结合吴消元法，获得了方程(1)的孤波解.李想等［3］利用平面动力系统理论对方程(1)的行波解对应的动力系统作定性分析，研究了方程(1)有界行波解的个数和所有可能存在的解形式.郭鹏等［4］利用Tanh-coth方法求解了非线性电报方程，得到了扭结状孤立波，奇异行波解和三角函数周期波解.

首次积分法首先由Feng［5］提出，其基本原理是对非线性发展方程做行波变换，化为常微分方程(组)，由可交换代数环理论找出一阶常微分方程(组)的首次积分，然后利用直接积分得到方程的精确解.实践证明，这个方法可以用来求解许多非线性发展方程的精确解［6－8］.基于此，本研究利用首次积分法讨论方程(1)的精确解.

1 首次积分法

除法定理［7］设 P(ω，z)是复数域 C［ω，z］上的多项式，并且P(ω，z)在 C［ω，z］上是不可约的，如果Q［ω，z］包含P(ω，z)的全部零点，那么在复数域C(ω，z)上存在一个多项式G(ω，z)使得，

对于含独立变量x，t的非线性发展方程，

式中，u=u(x，t)是未知函数，P是u和u的关于x和t的各阶偏导数的多项式.

利用首次积分法求解式(3)的主要步骤如下:

步骤1 通过行波变换将x和t转化为行波变量ζ，设定，

式中，ω为待定常数，式(4)就可转化为只含行波变量ζ的二阶常微分方程，

式中，u'=du/dζ，u″=d2u/dζ2.

步骤2 引入2个独立变量，X(ζ)=u(ζ)，Y(ζ)=u'(ζ)，则式(5)等价于一阶常微分方程组，

步骤3 设式(6)的首次积分形式为，

式中，ai(X)(i=0，1，…，m)(通常 m=2)，是实数域上的待定多项式.根据除法定理，存在实数域上的多项式α(X)，β(X)使得，

由式(8)确定多项式 α(X)，β(X)，进而求出P(X，Y).

步骤 4 将 X(ζ)=u(ζ)，Y(ζ)=u'(ζ)代入式(7)中，解之即可得到式(5)的精确解.

2 方程(1)的解

首先，将方程(1)进行行波变换，ζ=x－ωt，将ζ=x－ωt代入到方程(1)中，得到常微分方程，

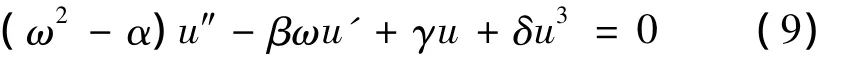
令，X(ζ)=u(ζ)，Y(ζ)=u'(ζ)，则式(9)的等价方程为，

式中，

根据式(10)和除法定理，可确定式(9)的首次积分.

设式(9)的首次积分的形式为，

式中，ai(X)(i=0，1，2，…，m)是实数域上的待定多项式.根据除法定理，存在实数域上的多项式α(X)，β(X)使得，

情形1 当m=1时，由式(13)两边Yi(i=0，1，2)的系数相等，即，

因为，ai(X)(i=0，1)均是X的多项式，由式(14)可以推出a1(X)是常数且β(X)=0.不失一般性，取a1(X)=1，将其代入式(15)，平衡α(X)和β(X)的次数，可得出，deg(α(X))=1，deg(a0(X))=2，不妨设，α(X)=A1X+A0，则由式(15)可得，

式中，D为积分常数.

将 α(X)，a0(X)，a1(X)代入式(16)，并令所有Xi的所有系数为零，得到，

解式(18)，得到2组解，

将上面的式(19)、(20)代入式(12)，可分别得到，

将 X(ζ)=u(ζ)，Y(ζ)=u'(ζ)分别代入式(21)、(22)，解得，

由此可得方程(1)的一组精确解为，

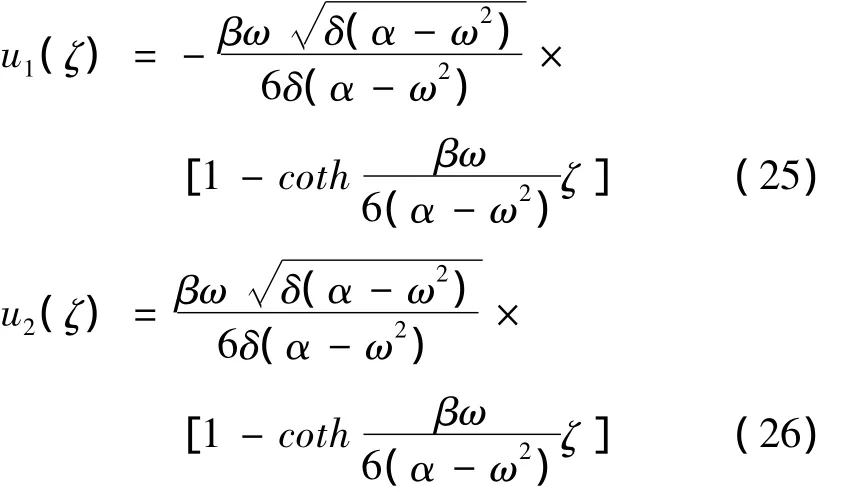
情形2 当m=2时，由式(12)两边Yi(i=0，1，2，3)的系数相等，得，

因为，ai(X)(i=0，1，2)均是X的多项式，由式(27)可以推出a2(X)是常数，且β(X)=0.不失一般性，取a2(X)=1，将其代入式(28)，平衡α(X)和β(X)的次数，可得出 deg(α(X))=0，或者deg(α(X))=1.事实上，如果 degα(X)＞ 1，设degα(X)=k(k ＞ 1)，由式(28)、(29)可知，dega1(X)=k+1，dega0(X)=2k+2，而由式(30)可知，k+4=3k+2，即k=1，这与k＞1矛盾.

当degα(X)=0时，取α(X)= α0，将其代入式(28)、(29)可得，

式中，G为积分常数.

将α(X)，a0(X)，a1(X)代入式(30)中，令X的同幂次项系数为0，得代数方程组，

解代数方程组(31)，得到2组解，

将式(32)代入式(12)，可得到，

式(33)可化简为，

将 X(ζ)=u(ζ)，Y(ζ)=u'(ζ)代入式(34)，运算可知其与m=1的结果相同.

当 degα(X)=1 时，取 α(X)=A5X+A4，将其代入式(26)、(27)可得，

式中，E、F为积分常数.

将 α(X)，a0(X)，a1(X)，a2(X)代 入 式 (30)中，令X的同幂次项系数为0，得代数方程组，

解式(37)～(42)，得，

将式(43)、(44)代入式(12)，可得到，

化简式(45)、(46)，得，

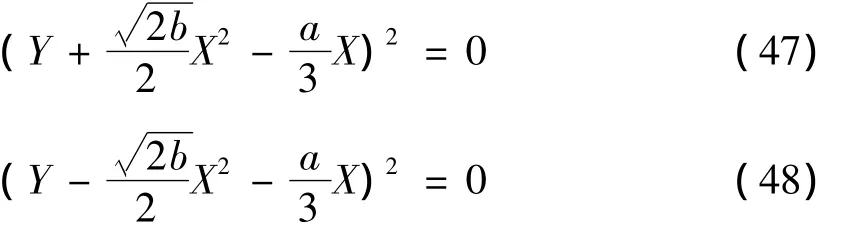
联立式(47)、(48)和式(12)，运算可知其与m=1的情况相同.

3 结论

近年来，许多学者应用首次积分法求解非线性发展方程的精确解.与双曲函数方法和辅助方程法直接求解方法相比较，首次积分法具有许多优点:首先，首次积分法不需要先对方程解的形式进行假设，再代入进行求解;其次，它在获得精确解的过程中，避免了求解复杂和繁琐超越方程的计算.

［1］Farlow S J.Partial differential equations for scientists and engineers［M］.New York:Wiley Interscience，1982.

［2］范恩贵，张鸿庆.非线性波动方程的孤立波解［J］.物理学报，1997，46(7):1254 －1258.

［3］李想，张卫国，赵岩.非线性电报方程行波解的定性分析与求解［J］.上海理工大学学报，2011，33(4):372 －378.

［4］郭鹏，陈宗广，孙小伟.非线性电报方程的简洁解法［J］.大学物理，2014，33(4):15 －17.

［5］Feng Z S.The first-integral method to study the Burgers-Korteweg-de vries equation［J］.Journal of Physics A:Mathematical and General Physics，2002，35(2):343 －349.

［6］黄欣.首次积分法下高维非线性偏微分方程新的行波解［J］.四川师范大学学报(自然科学版)，2014，37(3):312 －315.

［7］Bourbaki N.Commutative algebra［M］.Paris:Herman，Publishers in Arts and Science，1972.

［8］孙峪怀，杨少华，王佼，等.非线性Chaffee-Infante反应扩散方程的新精确解［J］.四川师范大学学报(自然科学版)，2012，35(3):293 －296.

First Integral Method and Its Applications in Nonlinear Telegraph Equation

LI Zhao，SUN Yuhuai，HUANG Chun
(College of Mathematics and Software Science，Sichuan Normal University，Chengdu 610066，China)

Based on the ring theory of commutative algebra，applying the first integral method，and combining the software of Maple，we obtain some new exact traveling wave solutions for the nonlinear telegraph equation.

first integral method;nonlinear telegraph equation;exact solution;division theorem

O175.29

A

1004－5422(2015)01－0029－04

2015－02－04.

四川省教育厅自然科学重点基金(2012ZA135)资助项目.

李 钊(1984—)，男，硕士研究生，从事非线性方程研究.