冻土导热系数的非线性规律研究

任小朋，樊红辉

(四川建筑职业技术学院，四川 德阳 618000)

冻土导热系数的非线性规律研究

任小朋，樊红辉

(四川建筑职业技术学院，四川 德阳 618000)

根据冻土多孔多相介质各组分随机分布的特性，结合随机模拟方法，应用有限元数值模拟软件COMSOL研究了导热系数与各影响因子之间的关系.计算结果表明:一定范围内的冻土土粒粒径以及含水量与导热系数表现为非线性关系，含水量与等效导热系数呈明显的非线性关系;在数量级较小的范围内导热系数与孔隙率以及未冻水含量表现为非线性关系.研究结果与实测结果和已有成果相符合，证明此方法是一种研究冻土物性参数的有效手段.

冻土;导热系数;未冻水含量;含冰量;非线性

0 引言

冻土，指的是含水的松散岩石或土壤，在0℃或0℃以下的环境温度下，转变成结晶状态或胶结松散的固体颗粒.冻土主要由矿物颗粒、冰晶体、未冻水(薄膜结合水和液态水)、气体(水蒸气和空气)组成.作为一种复杂的非均匀的多孔多相介质，其物理力学性质易受温度、水分等影响.

通常，测量冻土的导热系数有稳态和瞬态2种方法，国内外大多学者根据所研究的对象采用不同的测量手段和方法［1－5］.例如，赵秀峰等［6］采用基于瞬态平面热源法的Hot Disk热常熟分析仪测量了岩土的热物性参数，并得到了比较合理的测量结果.陶兆祥等［7］在比较法的测试原理的基础上，研制了针对大含水量的冻土导热系数测量仪器，并对兰州、东北等地的5种经典大含水量冻融土的导热系数进行了测量，取得比较满意的效果.谭贤君等［8］从多孔介质随机混合理论出发，提出了考虑相变以及未冻水对冻土导热系数的影响的计算公式，并利用有限元软件计算了冻土的导热系数，研究证明有限元软件在计算冻土的导热系数方面也能取得较好结果.

随着对冻土的不断深入研究，许多学者发现，冻土的物理参数是一个非线性的函数，受多种因素的影响，如土颗粒粒径、孔隙率、密度、含水量以及含冰量等.本研究从考虑冻土导热系数受颗粒粒径、孔隙率、未冻水含水量以及含冰量影响出发，建立微观冻土物理模型并进行数值模拟计算，基于热流计法的理论计算冻土的导热系数，并研究冻土导热系数变化规律，以期为冻土工程的发展提供理论和数据支持.

1 冻土导热系数模型

冻土作为一种多孔多相介质，其组成与普通土壤的区别在于含有冰晶体，而冰晶体在土壤中的存在对冻土的物理力学、热学性质有很大的影响.由于冻土的导热系数不同于普通土壤，需要考虑含冰量对导热系数的影响，而冰晶体作为一种容易相变的物质，其相变前后的导热系数差异巨大，主要表现为冰的导热系数是液态水导热系数的3倍左右.

此外，由于冻土是由矿物颗粒、冰、水和气体组成的多相介质，其导热系数取决于冻土体的孔隙率、未冻水含量、含冰量与含气量，以及各组分的导热性能以及温度等，通过建立微观冻土物理模型并进行数值模拟计算，成为分析与研究冻土导热系数变化规律的一个重要手段［4，8－9］.

1.1 基本假定

本研究根据多孔多相介质各组分在空间上具有随机分布的特性［10］，通过计算导热系数的稳定法，建立预测宏观等效导热系数的计算模型来计算不同工况下冻土的导热系数.

本研究提出的计算模型需设定的基本假定如下:导热系数各向同性;各组分为均质材料;各组分为立方体且尺寸相当，即孔隙尺寸与颗粒粒径等相等;各组分在空间分布上具有随机性.

1.2 有限元计算模型

根据多孔多相随机混合介质理论，将冻土各组分按一定比例随机分布在模型中:孔隙率为40%，未冻水含量为25%，含冰量为6%，单元总数为1000，各组分随机分布的冻土微观三维有限元计算模型见图1所示.

图1 冻土微观三维有限元模型示意图

1.3 控制方程及计算公式

冻土导热系数是表示冻土体导热能量的指标，它的测试具有一定的特殊性，即必须维持冻土试样的低温状态.

当仅考虑热传导、冰水相变作用，而忽略热对流、热辐射等时，冻土体三维稳态热传导控制方程［14］为，

式中，λx、λy、λz分别为 x、y 及 z方向的导热系数，W/m·℃;T为温度，℃.

基于本研究建立的有限元计算模型以及控制方程，采用热流计法研究冻土的导热系数.

热流计法的理论基础是根据傅里叶提出的一维热传导方程，在研究冻土导热现象时，确定了导热所传递的热流量Q与温度梯度的绝对值和垂直于热流的截面积A成正比，由于热流的方向与温度梯度的方向相反，则，

式中，λ为导热系数，W/(m·℃);Q/A为通过单位面积的热流量，称为热流密度，用q表示，W/m2.则式(2)可写为，

对测试各向同性、具有规则几何形状的试样时可表示为如下形式，

将式(5)带入式(4)可改写为，

导热系数在数值上等于单位温度梯度(1℃/m)作用下物体内所产生的热流密度.由于假定导热系数各向同性，因此只需计算一个方向的导热系数，本研究以计算Z方向的导热系数作为冻土等效导热系数.Z方向的导热系数公式如下，

式中:q为通过计算模型的平均导热热流密度，W/m2;h为计算模型的高度，m;Tup、Tdown分别为计算模型的上边界条件和下边界条件，℃.

2 结果及分析

2.1 结果

哈尔滨漠河区域地处多年冻土地区，以该地区的冻土作为研究对象具有代表意义，本研究所分析对象的冻土土工参数及其颗粒组成见表1.

表1 冻土的土工参数及其实测颗粒组成

采用多孔介质传热模型，模型的四周为绝热边界条件，上下边界面的温度边界条件Tup、Tdown根据未冻水含量(含冰量)推算，各计算单元根据组分类型定义其导热系数.利用式(1)进行模拟计算，最后按式(6)统计给出冻土微观模型的等效导热系数.

为验证本实验的合理性，给出了计算值与实测值之间的相对误差如表2所示.

表2 计算值与实测值统计数据对比

计算结果表明，本方法可较好地模拟冻土的导热系数.

2.2 分析

2.2.1 土壤粒径.

图2为冻土矿物颗粒平均直径与等效导热系数的曲线关系.结果表明，冻土的导热系数随颗粒平均直径增大而增大，表现为线性关系.不同土体的导热系数的曲线斜率有所差别，当颗粒粒径较小，其增长速率较快;而当粒径较大时，增长速率较小;粒径越大，其等效导热系数值也越大.

图2 颗粒平均粒径与导热系数的关系

2.2.2 土壤孔隙率.

图3为土体孔隙尺寸分别为0.01 mm和0.02 mm时的等效导热系数与孔隙率的关系.可以看出，冻土的导热系数随孔隙率的增加而减小，冻土的导热系数在孔隙率小于0.42时表现为非线性关系，当孔隙率超过某一范围时表现为线性关系.数值计算结果表明，冻土密实度越大，其导热系数越大.

图3 孔隙率与导热系数的关系

2.2.3 未冻水含量.

一般情况下，未冻水含量愈低，导热系数值愈大.这是因为未冻水含量较低，固体颗粒以及含冰量含量较大，这两者的导热系数比水的导热系数大3～4倍.图4显示为土壤颗粒平均粒径分别为0.01 mm和0.02 mm时，未冻水含量与等效导热系数的关系.曲线显示，随着未冻水含量的增加，冻土的导热系数呈单调递减的趋势，关系曲线为一近似线性函数.

图4 未冻水含量与导热系数的关系

土颗粒粒径为0.01 mm时的函数关系式，

土颗粒粒径为0.02 mm时的函数关系式，

2.2.4 含冰量.

含冰量是影响冻土导热系数的一个极其重要因素.图5为土壤颗粒平均粒径分别为0.01 mm和0.02 mm时，含冰量与等效导热系数的关系.导热系数随着含冰量的增加而增加.这主要是由于含冰量的增加会导致未冻水含量下降，而冰的导热系数比水大很多倍.此外，含冰量的增加减少了土体中的孔隙，致使空气所占比例减小，从而使冻土导热系数的急剧增加.

图5 含冰量与导热系数的关系

2.2.5 含水量的影响.

图6为土壤颗粒平均粒径分别为0.01 mm和0.02 mm时，总含水量与等效导热系数之间的关系.结果表明，随着总含水量的增加，冻土的导热系数不断增大曲线斜率不断下降.主要是黏土、粉土的颗粒尺寸较小，粒径较小的颗粒吸水性较强，当吸收的水分超过最大吸水量时，水分对矿物颗粒间的联系作用减弱，表现为导热系数增长缓慢.含水量与导热系数的关系曲线为非线性型，曲线表现为一抛物线型，拟合曲线给出函数关系式.

土颗粒粒径为0.01 mm时的函数关系式，

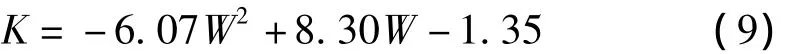
土颗粒粒径为0.02 mm时的函数关系式，

图6 总含水量与导热系数的关系

3 结论

冻土作为一种多孔多相介质，由于受温度、应力及水分的影响，其导热系数受多重因素的相互作用.本研究根据冻土多孔多相介质各组分随机分布的特性，结合随机模拟方法，应用有限元数值模拟软件研究了导热系数与各影响因子之间的关系.

研究结果表明:导热系数随矿物颗粒粒径、含冰量及含水量增加而增大，且矿物颗粒粒径值较小时表现为非线性关系;含冰量与导热系数主要呈线性关系;而导热系数随含水量增加而增加，但曲线斜率逐渐减小，表现较强的非线性关联;孔隙率以及未冻水含量的增加会导致导热系数的下降;相关曲线显示，当孔隙率较低时，导热系数与孔隙率表现为非线性关系，而当孔隙率超过一定值，两者表现为线性关系.

需要说明的是，由于计算模型是一种理想化的模型，同时未考虑密度、含盐量等对导热系数的影响，数值计算的结果在局部上与实测值存在一定的差异，这也是下一步工作需要着重考虑的问题.

［1］徐学祖，王家澄，张立新，等.冻土物理学［M］.北京:科学出版社，2001.

［2］Gustafsson S E，Suleiman B.The transient plane source technique:experi-mental design criteria［J］.High temperatureshigh pressures，1991，23(1):289 －293.

［3］陈桂生，廖艳，曾亚光，等.材料热物性测试的研究现状及发展需求［J］.中国测试，2010，36(5):5 －8.

［4］吕兆华.泡沫型多孔介质等效导热系数的计算［J］.南京理工大学学报，2001，25(3):257 －261.

［5］徐慧，杨杰.瞬态热带法和瞬态平面法测量材料热传导系数［J］.测控技术，2004，23(11):71 －73.

［6］赵秀峰，曹景洋，罗惠芬.采用Hot Disk测量岩土热物性的实验研究［J］.中国测试，2012，38(4):106 －109.

［7］陶兆祥，张景森.大含水(冰)量融冻土导热系数的测定研究［J］.冰川冻土，1983，5(2):75 －80.

［8］谭贤君，褚以忄享，陈卫忠，等.考虑冻融影响的岩土类材料导热系数计算新方法［J］.岩土力学，2010，31(2):70－74.

［9］刘焕宝，张喜发，赵意民.冻土导热系数热流计法模拟试验及成果分析［J］.冰川冻土，2011，33(5):1127 －1131.

［10］刘建军，代立强，李树铁.孔隙介质渗流微观数值模拟［J］.辽宁工程技术大学，2005，24(5):680 －682.

Nonlinear Law Research of Heat Conductivity for Frozen Soil

REN Xiaopeng，FAN Honghui
(Sichuan College of Architectural Technology，Deyang 618000，China)

According to the permafrost characteristics of the random distribution of components of porous multiphase medium，using the stochastic simulation method and the finite element numerical simulation software COMSOL，this paper studies the relationship between the coefficient of thermal conductivity and the influence factors.The calculation results show that a certain range of the permafrost soil grain size and the water content and the coefficient of thermal conductivity performance have nonlinear relation，and the nonlinear relation of the water content and the coefficient of equivalent thermal conductivity is obvious.Within the scope of the smaller order of magnitude，the relation among the thermal conductivity coefficient and the porosity and the unfrozen water content is characterized by the nonlinear relation.The research results have been consistent with the measured results and the previous research，which proves that such method is an effective means to study the physical property for frozen soil.

frozen soil;thermal conductivity;unfrozen water content;ice content;nonlinear

TU445;P642.14

A

1004－5422(2015)01－0101－04

2014－12－22.

任小朋(1981—)，男，硕士，工程师，从事工程结构与抗震防灾研究.