基于信息素更新和挥发因子调整的改进蚁群算法

孟晓琳，黄天民，陈尚云

(西南交通大学 数学学院，四川 成都 611756)

0 引 言

20 世纪90年代，学者Macro Dorigo 首先提出了蚁群算法，其迅速成为启发式算法研究的热点，它在解决传统算法无法解决的组合优化和NP 等难题上能够取得很好的效果，并且具有解决复杂问题的能力.同时，蚁群算法的鲁棒性较强，能进行分布式计算，同其他优化算法结合容易，而且算法没有复杂的数学操作，对软硬件要求不高，但是该算法搜索时间较长，很容易陷入局部最优解［1－2］.为了克服蚁群算法的缺点，许多学者对其进行了研究，并提出了相应的改进算法［3－6］.在此基础上，本研究提出一种将信息素局部更新和全局更新相结合，并对挥发因子ρ进行分段设置，以此来增强蚁群算法的全局搜索能力，并采用TSP 实例对算法进行验证，证明了本改进算法的有效性.

1 蚁群算法的基本原理

设m 表示蚂蚁的数量，dij(i，j = 1，2，…，n)表示城市i、j 之间的距离，bi(t)表示t 时刻位于城市i的蚂蚁个数，则，表示t 时刻在i和j 连线上残留的信息素，初始时刻，各路径上的信息素浓度相等，设τij(0)= C，C 为常数.

在搜索过程中，每只蚂蚁根据状态转移概率来判断路径的选择，t 时刻蚂蚁k 由城市i 到j 的状态转移概率用来表示，

每只蚂蚁对路径做出选择后将移动至下一城市，并且将当前蚂蚁所在城市放入禁忌表tab uk中，当禁忌表包含所有城市时，表示已经完成一次迭代，计算每只蚂蚁所走的路径并保留最短路径.

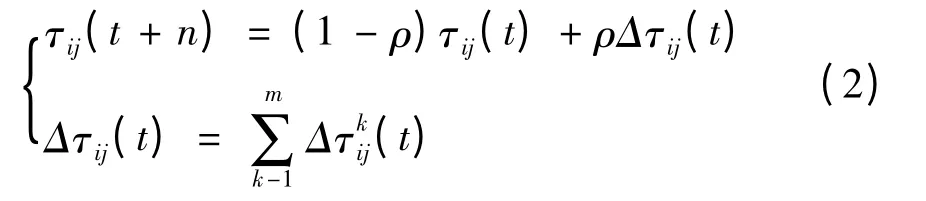
路径上的信息素会随着时间的推移而渐渐减弱，经过n 个时刻，路径ij 的信息素将按照式(2)进行更新，式中，ρ 表示信息素挥发因子，Δτij(t)表示本次迭代中路径ij 上的信息素增量，表示第k 只蚂蚁在本次迭代中留在路径ij 上的信息素，其表达式为，

式中，Q 表示常数，Lk表示第k 只蚂蚁在本次迭代中走过的路径长度［4］.

2 蚁群算法的改进

本研究对基本蚁群算法做了2 点改进:其一，针对基本蚁群算法容易出现早熟和停滞现象，进行了信息素更新的改进;其二，为了使算法的全局搜索能力和收敛速度均得到提高，进行了信息素挥发因子的改进.

2.1 信息素的局部更新与全局更新

在基本蚁群算法中，信息素的更新方式有可能导致这样的现象:新的最优路径尚未出现时，当前最优路径上的信息素就会按照信息素更新公式不断增多.这使得当前最优路径上的信息素可能会因为过度增多而大于新的最优路径上信息素，最终导致算法停滞.对此，本研究提出一种局部更新和全局更新信息素结合的方法，其思路是:

对于第k 只蚂蚁，它每经过一条路径ij，设经过该路径的时间为n，则在时刻t + n，该路径上的信息素会用式(4)进行更新.

式中，ρ 为信息素挥发因子;τij(0)为信息素初始值.当蚂蚁k 经过(i，j)时，式(4)就会减小该路径上的信息素，降低其他蚂蚁选中该路径的概率，增加探索其他边的机会.相较于基本蚁群算法，此改进可以避免因某一路径信息素累计量过大而导致算法停滞.

同时，每次迭代结束以后，对于当前最优路径上的信息素用式(5)进行全局动态更新，

中华民族五千年的发展和奋斗史使我们清楚的明白，一个民族的物质财富只是民族财富的外在形式，而真正起决定作用、内在的财富是这个民族的文化，它发挥着巨大的精神作用。文化强则国强，精神富则国富。引进剧是外来文化中独树一帜的新生力量，是我们接收外来文化的一种新的发展趋势，我们应该认真对待，使引进剧在马克思主义哲学的事业下符合21世纪的东方与西方文化建设的方向，在物质生活飞速发展的形势下增强人民精神世界的获得感、幸福感和满足感。

式中，Δτij(t)为全局更新信息素增量，LNC为当前迭代即第NC 次迭代的最优路径长度，Lbest为当前最优路径长度.

此改进有利于蚂蚁根据当前最优路径动态地调整信息素，随着迭代进行，有更优路径出现后，LNC和Lbest的差值会逐渐减小.相应地，信息素增量减小直至0，此时，当前最优路径上只进行信息素蒸发.与基本蚁群算法相比，这样能使当前最优路径上的信息素浓度更为突出，但又不至于造成算法停滞，使当前最优路径的变化更快地反映在信息素分布上.

2.2 分段调整信息素挥发因子

蚁群算法中，信息素挥发因子ρ 的大小直接关系到算法的全局搜索能力和收敛速度，基本蚁群算法中的ρ 是(0，1)区间的某个固定值.当ρ 过小时，已经被搜索过的路径被再次选择的可能性过大，容易出现局部收敛;反之，当ρ 过大时，虽然可以提高算法的随机性能和全局搜索能力，但又会使算法的收敛速度降低［6］.对此，本研究提出一种分段调整信息素挥发因子的方法，即随着迭代次数的增加，将算法分为初期、中期和后期.在算法初期，将ρ 设置为较大的值，这样可以使算法的全局搜索能力增强，在中期和后期适当减小ρ 的值，使得算法可以较快地收敛到最优解.这样既增加了算法的全局搜索能力，又可以在一定程度上加快算法的收敛.具体规则为，

其中，NC 表示算法的迭代次数，NC－max 表示最大迭代次数.

在整个迭代过程的前四分之一，将ρ 取值为最接近1 的值0.9，可以在初始阶段提高算法的全局搜索能力;然后，将ρ 设置为中间数值0.5，使算法既不至于陷入局部收敛，又能加快收敛速度;到了迭代过程的后四分之一，将ρ 值取为0.1，因为此时的搜索结果已经基本确定，适时可以加快算法的收敛速度.

2.3 算法实现

根据以上的改进思路，改进后的算法实现的具体步骤为:

1)参数初始化α，β，Q，NC－max，m，令迭代计数器NC = 1.

2)随机选择每只蚂蚁的初始位置，初始化禁忌表tk，按照式(6)设置ρ 的值.

3)按照式(1)选择路径，将所选城市添加到tk中，并按照式(4)更新局部信息素.

4)若tk未满则转至步骤3)，若已满，得出蚂蚁此次的最优路径长度LNC，并更新Lbest的值.

5)对当前的最优路径按照式(5)更新全局信息素，清空tk.

6)若NC ＜NC－max，则NC = NC +1，并转至步骤2)，开始新一次的迭代，否则算法结束，输出最优路径长度Lbest.

3 仿真实验及结果分析

在仿真实验中，选用TSP LIB 中的Oliver 30 和att 48 作为仿真算例，以验证本研究提出的改进算法性能，并与基本蚁群算法求解Oliver30 TSP 和att48 TSP 进行比较.

基本蚁群算法采用的参数为:α = 1，β = 2，ρ =0.5，Q = 100，NC－max = 200，m = 30［7］;本研究提出的改进算法的参数为:α = 1，β = 2，Q = 100，NCmax = 200，m = 30.对2 种算法分别测试20 次，其结果如表1、2 所示.

表1 对Oliver30 TSP 测试20 次的结果

表2 对att48 TSP 测试20 次的结果

从表1、2 可以看出，经过20 次的测试，采用本基本蚁群算法改进的算法求解Oliver 30 和att 48 所得最优值、最差值和平均值与基本蚁群算法相比均有所改善.

另外，在收敛速度上，本研究算法在150 代以内几乎可收敛到最优值，但基本蚁群算法在180 代到200 代依然存在多次尚未收敛的情况.2 种算法的最短距离及收敛情况如图1、2、3、4 所示.图1 和图2分别是基本蚁群算法测试att48 TSP 问题的某一次最短距离和收敛情况.

图1 基本蚁群算法测试att48 TSP 问题的最短距离

图2 基本蚁群算法测试att48 TSP 问题的收敛情况

图3 和图4 分别是改进算法测试att48 TSP 问题的某一次最短距离和收敛情况.

图3 改进算法测试att48 TSP 问题的最短距离

图4 改进算法测试att48 TSP 问题的收敛情况

由实验结果可见，随机选择的某一次实验结果中，基本蚁群算法测试att 48 的最短距离是35 701.8073 km，收敛速度较慢，在迭代180 次之后仍未收敛;改进算法测试att 48 的最短距离是34 751.3419 km，收敛速度明显提升，在迭代150 次左右达到最优.此表明，在求解Oliver 30 和att 48 问题上，本改进算法在求最优解和收敛速度上有明显优势.

4 结 语

本研究通过引入信息素局部更新和全局更新相结合，以及分段式更新信息素挥发因子的方法，对基本蚁群算法进行了改进，达到了扩大解的搜索空间、兼顾搜索速度和搜索能力的目的.改进算法的性能在Oliver 30 和att48 问题上已经得到验证，但对于更大规模的数据，改进的算法是否能够使用还有待于进一步的研究.

［1］王运涛，姚砺，毛力.基于混合行为的自适应蚁群算法［J］.计算机仿真，2009，26(12):151－153.

［2］段海滨，王道波，于秀芬.蚁群算法的研究现状及其展望［J］.中国工程科学，2007，9(2):98－102.

［3］方霞，席金菊.基于变异和启发式选择的蚁群优化算法［J］.计算机工程与应用，2013，49(24):24－27.

［4］李成兵，郭瑞雪，李敏.改进蚁群算法在旅行商问题中的应用［J］.计算机应用，2014，34(S1):131－132，165.

［5］王沛栋.改进蚁群算法及在路径规划问题的应用研究［D］.青岛:中国海洋大学，2012.

［6］赵伟，蔡兴盛，曲慧雁.一种基于惩罚函数和新信息素更新方式的蚁群算法［J］.计算机工程与科学，2013，35(3):103－107.

［7］叶仕通，万智萍.一种基于改进全局信息素更新效率的蚁群算法及仿真［J］.计算机应用与软件，2014，31(1):176－179.