灰色－马尔科夫模型在大坝内部变形预测中的应用

沈哲辉，黄 腾，唐佑辉

（河海大学 地球科学与工程学院，江苏 南京210098）

对大坝内部水平位移进行监测是大坝安全监测系统中的重要组成部分，因此，对坝体内部水平位移数据进行分析，建立预测模型是十分必要的。灰色系统理论是研究系统分析、建模、预测、决策和控制的理论［1］，而传统的灰色 GM（1，1）理论预测模型存在精度差的问题［2］。针对大坝内部水平位移测点之间不是相互独立而是相互影响的，而且实际操作中样本的等时距性要求不容易满足，提出了一种非等时距的 MGM（1，n）－Mar kov模型。首先对原始数据进行等时距处理，再建立 MGM（1，n）模型。以灰色预测结果为基础，按照马尔科夫方法划分状态区间以及确定状态转移概率矩阵，进而求出新的预测值，提高预测精度［3］。

1 灰色－马尔科夫模型的建立

1．1 灰色 MGM（1，n）预测模型

MGM（1，n）建模过程如下：［4－6］

其中k＝1，2，…，m。

MGM（1，n）模型为n元一阶常微分方程组

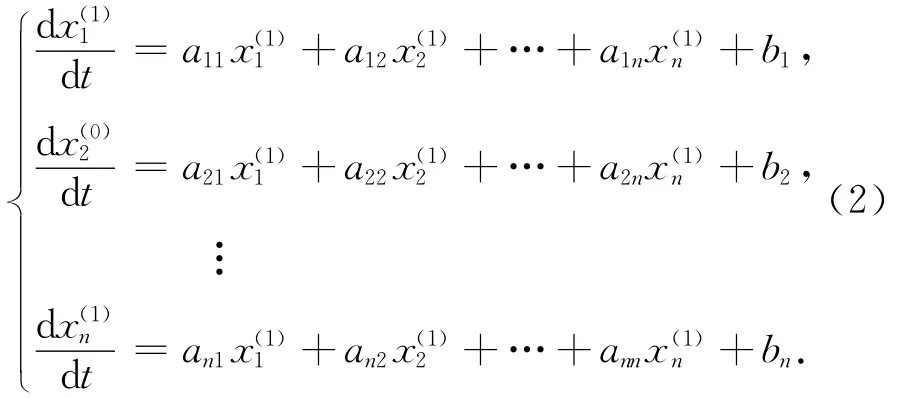
记

则式（2）可记为

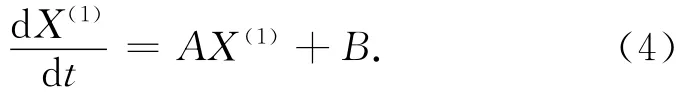
式（4）的连续时间响应为

X（1）（t）＝e（At）X（1）（0）＋A－1（e（At）－I）·B．（5）

其中

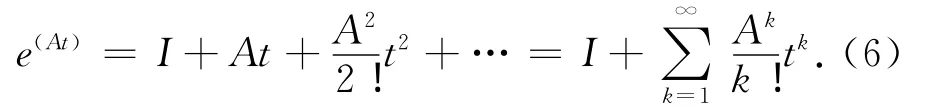
这里级数求和要取多少项才合适并不能简单地判断出来，因此，建议在MATLAB中用exp m函数求无穷级数。

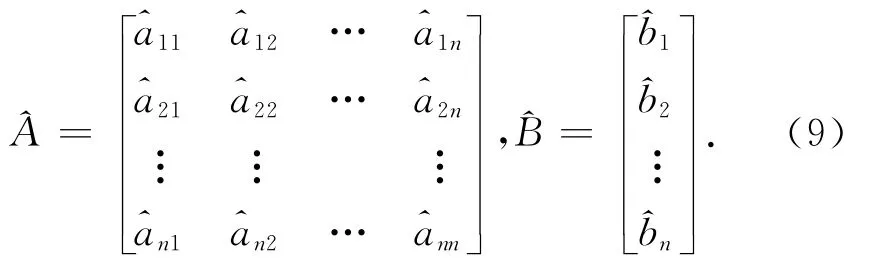
为了识别A和B，将式（2）离散化得到

记ai＝（ai1，ai2，…，ain，bi），i＝1，2，…，n。则由最小二乘法得到ai的辨识值

其中：

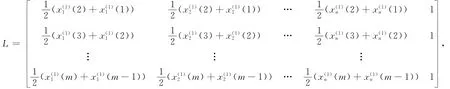
则得A和B的辨识值＾A 和＾B。

MGM（1，n）模型的计算值为

针对灰色模型只适用于等时距的数据，因此，把非等时距的原始观测数列化为等时距的数列是必要的。

1．2 非等时间间隔序列的处理

MGM（1，n）模型要求样本为等时距的，但实际过程中很难得到完全的等时距序列的样本。对于非等时距的数列，可以通过一定的方法化为等时距的数列，具体方法如下［7］：

令Δtk＝tk＋1－tk；

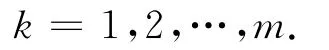
则可求得平均时间间隔

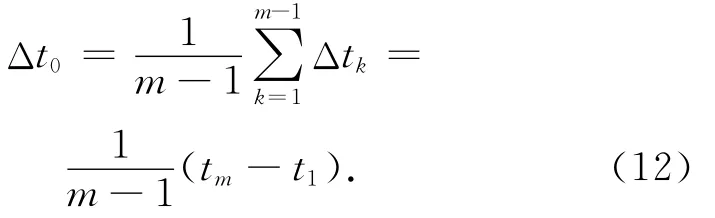
各时段与平均时段的单位时段差系数为

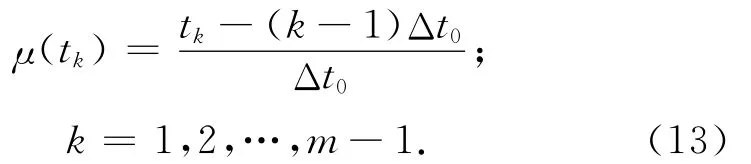
最终求得的等时距数列为

式（14）就是上述模型所需的等时距数列。等时距化后就可以建立 MGM（1，n）模型计算各期的拟合值并且进行预测，再建立马尔科夫模型来对实测值与拟合值之间的残差进行修正。

1．3 马尔科夫状态转移概率矩阵

马尔科夫模型建立的方法和步骤［2］如下：

1）状态的划分：计算出预测数值与实测数值的残差序列，并据此划分h个状态区间

3）h步状态转移概率矩阵是一步状态转移概率矩阵的h次方，即

以上介绍了本文用到的方法和模型，下面介绍把它们结合在一起的具体过程。

1．4 Markov残差修正的 MGM（1，n）模型建立

本文构建大坝内部水平位移的多变量灰色预测模型，使用Mar kov模型对残差序列进行修正，构建基于Mar kov残差修正的灰色 MGM（1，n）模型的建模步骤如下：

1）选取位于大坝某高程处测房内的3个测点从2012－03－22到2013－06－21的15期测值，按式（12）、式（13）、式（14）把它们15期的非等时距的数据化为等时距的，得到的15期数据为（k），i＝1，2，3；k＝1，2，…，15。

4）根据εi（k），k＝1，2，…，15划分状态，这里对每个测点的各期相对误差统一划分状态，计算出各自的一步状态转移概率矩阵。

2 实例分析

2．1 历史数据

本文为验证基于Mar kov残差修正的灰色MGM 1 n模型的正确性和可靠性，利用大坝内部水平位移观测数列为历史数据进行建模分析。大坝内部水平位移指的是大坝内部顺河向的水平位移，即沿着水流方向的位移，大坝内部布有引张线水平位移测点，张线式水平位移计的工作原理是：在测点高程水平铺设能自由伸缩的管路，从各测点引出线膨胀系数很小的不锈钢铟瓦合金钢丝，通过导向滑轮，在其终端加若干张拉平衡砝码，测点相对观测房固定端移动时，带动钢丝移动，在固定标点处用游标卡尺测出钢丝的位移量，算出测点的相对水平位移。下面以某大坝某高程处坝内3个水平位移测点从2012－03－22到2013－06－21的数据为历史数据，如表1所示。

表1 原始监测序列

表1中的这15期观测数列是非等时距的，2012－03－22的观测数据在本文中是第1期观测数据，为方便等时距化，把2012－03－22记作观测的第1天，2012－04－18就为观测的第28天，依次类推，2013－06－21就为观测的第457天。

2．2 等时间间隔化并建立 MGM（1，n）模型

2．3 马尔科夫残差修正

根据表2计算出各测点每期的拟合值与真实值的相对误差，见表3。可以看出3个测点各期相对误差在［－5．2，3．2］的区间内，划分4个状态区间［－5．2，－2］，［－2，0］，［0，1．5］，［1．5，3．2］。然后对各测点划分状态，详细状态划分见表3。

表2 等时距序列以及拟合值

表3 相对误差状态划分

写出各自的一步状态转移概率矩阵，这里以测点1为例。状态1出现2次，状态2出现4次，状态3出现5次，状态4出现2次（去除最后一个状态）。再根据状态x一步转移到状态y出现的次数，求出一步状态转移概率矩阵

编制预测表格：由于将状态划分4个，所以选择离预报时刻（2013－07－22）最近的4年编制预报表，其转移步数分别定为1，2，3，4，得到新的转移概率［8］，见表4。

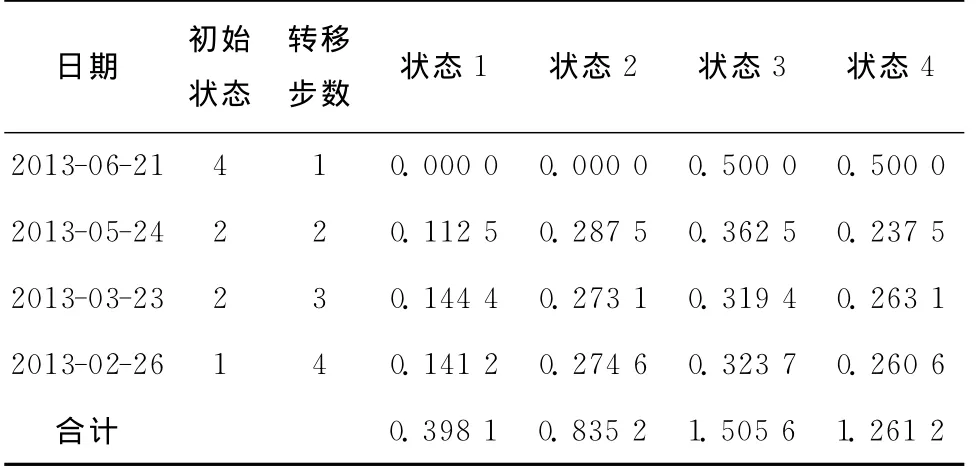
表4 状态预测

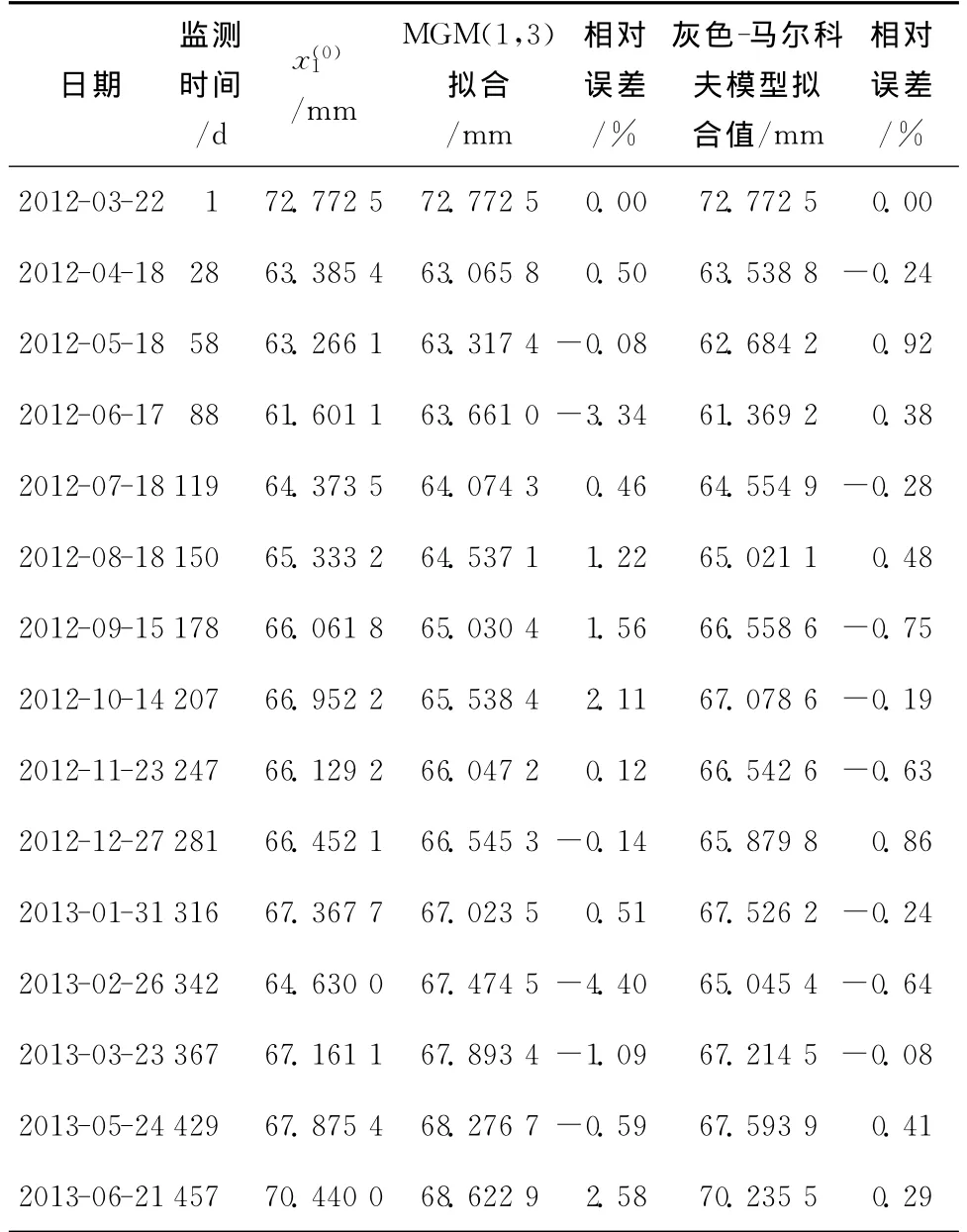
表5 测点1拟合结果比较

图1 测点1拟合值相对误差比较图

从表5可以计算出测点1的MGM（1，3）拟合结果相对误差的绝对值的平均值为1．25%，而灰色－马尔科夫拟合结果的相对误差的绝对值的平均值为0．43%。从图1中可以看出，测点1的灰色－马尔科夫拟合值相对误差折线比灰色模型拟合值相对误差折线平稳，灰色－马尔科夫拟合值相对误差总体上比灰色模型拟合值相对误差小。

同理，可求出测点2在2013－07－22的预测值为80．546 8 mm，用灰色马尔科夫模型修正的值为81．150 9 mm，实测值为83．29 mm。MGM（1，3）预测值得相对误差为3．29%，残差修正后的相对误差为 2．57%；测 点 3 在 2013－07－22 的 预 测 值 为97．321 5 mm，用灰色马尔科夫模型修正的值为98．051 4 mm，实测值为99．85 mm。MGM（1，3）预测值的相对误差为2．53%，残差修正后的相对误差为1．80%。

用灰色－马尔科夫模型对测点2和测点3在2012－03－22至2013－06－21的位移量进行拟合。图2为测点2的灰色－马尔科夫模型拟合值相对误差与灰色模型拟合值相对误差比较图；图3为测点3的灰色－马尔科夫模型拟合值相对误差与灰色模型拟合值相对误差比较图。

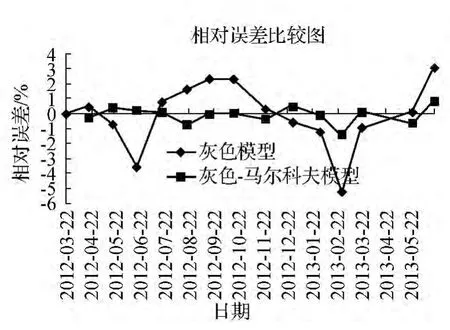
图2 测点2拟合值相对误差比较图

图3 测点3拟合值相对误差比较图

经计算，测点2的MGM（1，3）模型拟合结果相对误差的绝对值的平均值为1．54%，而灰色－马尔科夫拟合结果相对误差的绝对值的平均值为0．37%；测点3的 MGM（1，3）模型拟合结果相对误差的绝对值的平均值为1．22%，而灰色－马尔科夫拟合结果相对误差的绝对值的平均值为0．54%。从图2和图3可以看出，测点2和测点3的灰色－马尔科夫拟合值相对误差折线均比灰色模型拟合值相对误差折线平稳，两点的灰色－马尔科夫拟合值相对误差总体上比灰色模型拟合值相对误差小。

综上可见，灰色－马尔科夫模型的模型精度比灰色模型的拟合精度高。从对3个测点2013－07－22的灰色－马尔科夫模型预测的结果和灰色模型预测的结果比较看出，灰色－马尔科夫模型的预测精度高于灰色模型的预测精度。

3 结束语

本文通过对某大坝内部水平位移的实测数据建立非等时距的灰色－马尔科夫模型，解决了实际测量中样本序列不等时距的问题，得到了灰色－马尔科夫模型不仅比单一的灰色模型的拟合精度高，而且预测精度也比灰色模型的预测精度高，具有一定的实际应用价值。本文中Mar kov模型建立在灰色模型之上，其状态区间是随机划分的，所以预测结果会随着状态区间划分的不同会有略微的差异，如何划分状态区间使得灰色－马尔科夫的拟合精度和预测精度尽可能的高还有待进一步研究。

［1］ 唐争气，谭志强．灰色时序组合模型在基坑监测中的运用［J］．测绘工程，2014，23（2）：49－53．

［2］ 时合生，樊爱宛，王巍．用马尔可夫残差修正灰色理论的煤炭需求预测［J．计算机仿真，2011 28 10 187－190．

［3］ 李明然，田林亚，洪毅．改进的灰色马尔科夫模型在大坝变形预测中的应用［J］．水利与建筑工程学报，2012，10（3）：65－66．

［4］ 翟军，盛建明．MGM（1，n）灰色模型及运用［J］．系统工程理论及实践，1997，17（5）：109－113．

［5］ 孙小三，孙志久，范庆来．MGM（1，n）模型在软土路基沉降预测中的运用［J］．中南公路工程，2005，30（3）：145－147．

［6］ 邓聚龙．灰色理论基础［M］．武汉：华中科技大学出版社，2002．

［7］ 陈斌，陈晓冬，张仪萍．MGM（1，n）模型在粉喷桩路基沉降预测中的运用［J］．辽宁工程技术大学学报，2007，26（3）：378－380．

［8］ 毛占利，朱毅，杨伯忠，等．火灾事故的灰色－马尔可夫模型 预 测 研 究 ［J］．中 国 工 程 科 学，2010，12（1）：98－101．

［9］ 臧文亚，周仲礼，龚灏，等．基于灰色马尔科夫模型的重庆市水运货运量的预测［J］．水运 工程，2012（1）：30－33．

［10］唐文清，全美杰，曹玲玉，等．基于灰色理论－马尔可夫模型对畜禽粪便量增长的预测［J］．衡阳师范学院学报，2009，30（6）：128－131．

［11］孙泽信，庞逸群，黄腾．改进的灰色模型在建筑物沉降预测中的应用［J］．测绘工程，2010，19（3）：59－62．