基于规则格网DEM线状矢量要素三维可视化方法

程绵绵，李少梅，朱新铭，程见桥

（1．信息工程大学 地理空间信息学院，河南 郑州450001；2．北京理工大学 信息与电子学院，北京100081）

矢量数据是表示空间对象信息的一种重要数据结构，是进行各种深入研究工作的重要信息资源［1］。规则格网DEM能够描述地形的高程信息，采用地形格网可以模拟地球表面的起伏。矢量数据与三维地形的无缝融合是恢复空间对象真实面貌的重要手段［2］。随着三维地理信息系统、三维制图及虚拟现实技术的发展，矢量数据与三维地形的无缝叠加及符号化成为研究的热点与难点问题。在三维地理信息系统方面，三维地形无缝叠加矢量数据主要是为了在三维空间中进行空间分析和量算；在三维制图方面，主要是将三维地形及矢量基础地理信息以更直观的方式统一呈现，制作三维地图；在虚拟现实方面，主要是综合利用DEM数据及矢量基础地理信息数据构建虚拟地理环境。面向制图的矢量数据与三维地形无缝叠加强调的是矢量数据在三维地形表面的叠加及符号化效果，以更直观有效的方式传递地图信息，而不是叠加及显示的实时性。

现阶段，矢量数据与三维地形的无缝叠加主要有3种方法：几何法［3］、纹理法［4］及阴影 体算法［5］，这3种方法各有不同的特点及适用领域。从三维制图的角度来讲，为了使制图过程更加灵活，需要从DEM数据及矢量数据出发，分别实现DEM数据三维可视化及矢量数据符号化，其思想相当于将传统二维制图平面变成三维地形表面，将矢量数据“放到”地形表面后实现其符号化［6］。现有的几何法能实现矢量数据与三维地形的无缝叠加，但没有考虑后续的矢量数据符号化过程，使得矢量数据的显示过于简单，从而导致地图要素信息传递受限［7］。本文以线状矢量要素为例，提出了一种基于几何法的线状矢量数据与规则格网DEM无缝叠加的方案，并在此基础上通过纹理映射的方式实现线状要素的符号化。

1 基于几何法的线状要素与规则格网DEM叠加算法

矢量数据是通过坐标值来精确地表示点、线、面等地理实体，线要素矢量数据通常用来表示道路、河流等线状基础地理信息；规则格网DEM数据可以通过构建地形三角网的方式实现地形三维可视化。几何法是根据矢量数据与地形三角网的交点进行插值计算，实现矢量数据与三维地形的无缝叠加。为了让矢量数据显示时具有一定的宽度，常常将矢量数据扩展一定的宽度后再执行叠加算法。这种方式比较灵活，可以根据实际需要决定如何扩展矢量数据以及扩展后如何与地形三角网进行交点计算。本文提出的算法分以下几步进行：

1．1 线状矢量数据结点高程值计算

对于矢量数据的一个结点P（x，y），计算其在三维地形表面对应的点P′（x，y，z），步骤如下：

1）根据P点坐标判断其落在哪个格网当中，假设为正方形ABCD，如图1所示，进而根据P点与AC直线的关系，判断P点在格网的哪个三角形中。

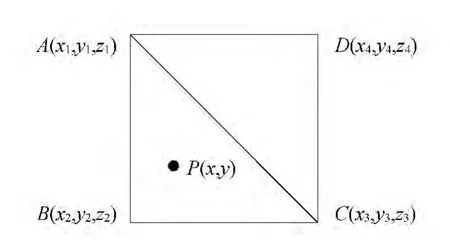
图1 点与地形三角网在平面上的投影

2）假设P点落在三角形ABC中，由于点A，B，C为DEM格网点，其三维坐标皆为已知，根据空间共面条件方程，可以求出P点的z坐标，求解方程如下：

1．2 线状矢量数据与DEM格网交点计算

计算得到矢量数据在DEM三角网上对应的新结点后，假设仅仅连接这些新结点，当这些结点不在三角网中同一个三角形中时，就会出现穿透或架空在三角网中的情形。为了让矢量数据紧贴地形表面，必须计算矢量数据与地形三角网的交点，让矢量数据紧贴着地形三角网中的每个三角形，并将这些交点增加到矢量数据结点当中，步骤如下：

1．2．1 计算矢量数据与DEM格网交点平面坐标

根据矢量数据相邻两个结点坐标计算其所在的直线方程，并根据两结点坐标值计算该线段跨越的横向和纵向的格网数，分别将横向格网的y值与纵向格网的x值代入直线方程，即可算出所有与格网交点的x，y坐标。

1．2．2 计算矢量数据与DEM格网交点高程值

矢量数据与格网的交点是空间任意一点的特例，因此可以按照1．1中所述方法进行计算。另外，由于矢量数据与DEM格网交点都在DEM格网上，计算交点的高程值只需在相邻DEM顶点上根据x坐标（交点在横向格网上）或y坐标（交点在纵向格网上）线性插值计算，这样计算公式更简单，此处不再赘述。

按照现有的几何法接下来应该计算矢量数据与地形三角网中跨越的三角形斜边的交点，但是因为很多时候矢量数据与格网的交点和与斜边的交点很近，如图2所示，为了避免给矢量数据增加过多的结点使矢量数据过于破碎，本文把线状矢量要素对地形的改造作用考虑进去，方法如1．3所述。

图2 矢量数据与格网的交点

1．3 线状矢量数据与规则格网DEM无缝叠加

按照上述方法叠加的矢量数据在数学意义上是没有宽度的直线，若在符号化时给矢量数据配置一定宽度的符号，由于矢量数据所在的地形表面一般不是水平面，这时会出现符号一半嵌入一半架空在地形上的情况。另外由于计算的矢量数据紧贴地形表面，在绘制过程中还会出现Z缓存混淆现象。

本文给出的解决方案是在构建地形三角网时就考虑到矢量数据符号的宽度，假设符号的宽度为w，矢量数据某结点处相邻线段的夹角为θ，如图3所示，则结点处符号的宽度为w／cos（θ／2）。因此，在矢量数据与地形格网交点处向所在直线垂直的方向水平扩展w／2距离增加顶点，在矢量数据结点处向角平分线方向水平扩展w／2cos（θ／2）增加顶点，以这些顶点构成的封闭条带为约束条件，约束地形三角网的构建。为了减少计算量，当线段斜率绝对值小于1时只取与纵向格网的交点（图4中AB段），大于1时只取与横向格网的交点（图4中BC段），这样能保证在小于一个格网的范围内在三维地形表面增加了新结点，不会影响矢量数据与三维地形的融合效果，且避免使矢量数据过于破碎。构建的约束条件及地形格网在平面上的投影如图4所示。

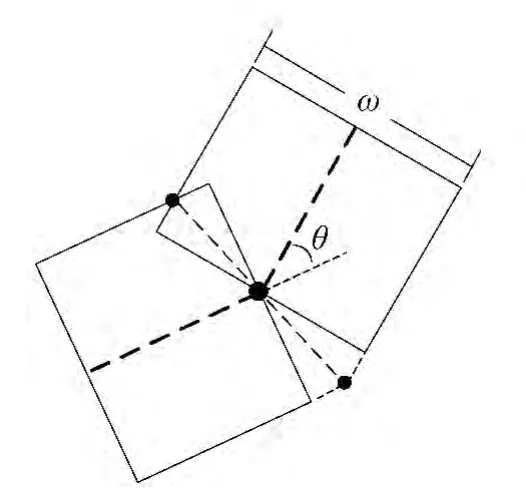
图3 结点处宽度计算

图4 构建的约束条件及地形格网在平面上的投影

这种方法可以使线状矢量要素比较均匀地叠加到三维地形上，且考虑到了矢量数据对三维地形的改造作用，比较符合实际情况。至此，线状矢量要素已扩展成为一定宽度的条带嵌入在三维地形中，在条带范围内配置一定的符号，就可以实现线状要素在三维地形表面的符号化。

2 基于三维地形的线状要素符号化

基于三维地形的符号化是指在地形表面叠加矢量数据后，给矢量数据配置符号。线要素常用的符号化方法有纵向配置图元法、横向配置图元法和函数法，其中横向配置图元法可用于绝大多数线状符号的绘制，其思想是将线状符号横向分解为最简单的重复单元，绘制时只用重复配置此单元。

由于要实现矢量数据与三维地形的无缝叠加，本文中的矢量数据已扩展成为一定宽度的条带，此时实现矢量数据的符号化可以沿着中轴线按照横向配置图元法给矢量数据配置与条带宽度一致的符号，这种方式类似于传统的在二维平面上的矢量数据符号化，会涉及到矢量数据转折点、交叉点处的关系处理等问题，难度较大。本文采用一种新的符号化方式，即在条带范围内重复配置符号图元，一个简单而有效的方式是使用纹理映射，使用纹理映射的好处是矢量数据转折点处的处理非常简单。这里的纹理是一个数组的概念，纹理可以是一个颜色数组，也可以是一张图片。将符号图元制作成纹理单元，在条带范围内重复贴此纹理单元，可以实现在三维地形表面的线状矢量要素符号化。

2．1 符号纹理的制作

现阶段使用的纹理类型较多，如一维纹理、二维纹理、三维纹理、立方图纹理等。这些纹理类型有不同的应用范围，本文对不同的线状符号选择二维纹理和一维纹理进行符号化。

2．1．1 二维纹理符号

这是应用最为广泛的一种纹理类型，它负责将二维矩形图像映射到三维物体之上。这种纹理基本可以实现所有的线状要素的符号化，纹理图元的制作可以通过PhotoShop、Ill ustrator等图形软件进行，要注意的是二维纹理高度和宽度通常为2n像素，如图5所示。

图5 符号纹理单元

2．1．2 一维纹理符号

如果将二维纹理的高度设置为1，则可视为一种只在一个方向上变化的一维纹理，这种方式只适合于沿着矢量数据方向不发生变化的符号，图5中的高速公路和普通公路纹理单元可以用一维纹理表示。虽然一维纹理实现的功能完全可以用二维纹理实现，但是一维纹理内存开销较小，用一维数组即可描述一个一维纹理，方法是依次将颜色值存入一维数组。

2．2 符号纹理的映射

在应用程序中实现纹理贴图通常需要以下4步：

1）创建纹理对象，并指定为一种纹理类型；

2）确定纹理如何应用到每个像素上；

3）启用纹理贴图功能；

4）绘制场景，提供纹理坐标和几何图形坐标。

其中最关键的是最后一步，即计算几何体每个顶点对应的纹理坐标。纹理坐标决定了纹理图像中哪个纹理单元将分配给某个特定顶点。在三维渲染引擎中，可以通过遍历几何体顶点计算适当的纹理坐标，也可以不用显示地分配纹理坐标，而是通过顶点坐标函数，由渲染引擎自动计算纹理坐标。

3 实 验

以某块区域规则格网DEM数据为例，在该区域内模拟3段不同类型的矢量数据，采用本文所述方法，利用Visual C＋＋2010和OSG开源库编程。其中OSG是一个基于工业图形标准Open GL的高层次图形开发API接口［8］，在实验中主要用来进行地形三维建模和实现纹理映射功能，其本身并不能实现矢量数据与三维地形的无缝叠加。矢量数据扩展一定宽度后叠加到规则格网DEM的地形三角网如图6所示；用分层设色方式实现地形三维可视化、分别用二维纹理实现铁路和高速公路符号化以及用一维纹理实现普通公路符号化的效果如图7所示。

图6 矢量数据扩展一定宽度后嵌入在地形三角网中

图7 矢量数据在三维地形表面的符号化效果

4 结束语

本文提出了一种在规则格网DEM表面无缝叠加线状矢量要素并实现矢量要素符号化的方法，通过实验，证明此方法行之有效。该方法可以对三维地形及矢量要素分别以不同的方式可视化，如对三维地形可以以不同的方式渲染，对矢量要素可以根据需要配置不同的符号，两者互不影响。这种方式在三维制图及构建三维虚拟地理环境方面具有一定的参考价值。由于本文以纹理映射的方式实现线状矢量要素的符号化，在显示效果及细节上还有所欠缺，下一步将研究新的符号化方法。

［1］ SCHNEIDER M，KLEIN R．Efficient and accurate rending of vector data on virtual landscapes［J］．Jour nal of WSCG，2007，15（1－3）：59－65．

［2］ 王娇娇．矢量数据三维可视化研究进展［J］．广东农业科学，2013（8）：183－188．

［3］ AGRA WAL A，RADHAKRISHNA M，JOSHI R．Geo metr y based mapping and rendering of vector data over LOD photo－textured 3D terrain models．Proceedings of WSCG［C］．Plzen：Czech Republic，2006．

［4］ BRUNETON E，NEYRET F．Real－ti me rendering and editing of vector－based terrains ［J］．Eurographics，2008，27（2）：311－320．

［5］ 刘昭华，杨靖宇，戴晨光．基于模板阴影体算法的矢量数据在三维场景中的绘制［J］．测绘工程，2009，18（1）：38－41．

［6］ 王祥峰，裴亮，丁波．基于ERDAS的数字校园三维可视化［J］．测绘工程，2014，23（4）：58－61．

［7］ 曹雪峰，万刚，李锋，等．三维地形环境中矢量地图实时符号化显示技术［J］．系统仿 真学报，2013，25（S1）：253－257．

［8］ 王锐，钱学雷．OpenScene Graph三维渲染引擎设计与实践［M］．北京：清华大学出版社，2009．