数字相机在类似棋盘检校场中的检校方法研究

张阳阳,门林杰,周桂初,杨　娟

(1.甘肃农业大学资源与环境学院,甘肃兰州730070;2.甘肃省国土资源规划研究院,甘肃兰州730000；3.中国地质大学信息工程学院,湖北武汉430074)

数字相机在类似棋盘检校场中的检校方法研究

张阳阳1,门林杰2,周桂初3,杨娟3

(1.甘肃农业大学资源与环境学院,甘肃兰州730070;2.甘肃省国土资源规划研究院,甘肃兰州730000；3.中国地质大学信息工程学院,湖北武汉430074)

摘要：针对众多非量测单相机的检校方法，通过分析数码相机的误差来源，并考虑相机的内、外方位元素和物镜光学畸变等因素引起的误差，提出一种基于类似棋盘检校场的数字相机检校方法。利用共线方程和二维DLT之间的关系导出了由二维DLT的9个参数表达的主纵线方程，构建同形矩阵，通过不同摄站拍摄目标的多幅影像，求得内、外方位元素的初始值，并由多张影像的空间后方交会求出相机需要检校参数，再由假设检验来检验相机系统参数的显著性。经实例分析表明，利用改进后的方法求解参数的精度满足实际需求，且效率更高。

关键词：内方位元素；外方位元素；畸变参数；同形矩阵；系统参数

随着科技进步，非量测数码相机以其低廉的价格、灵巧便携等特点在日常生活中得到了广泛应用，但由于它不能提供准确的内方位元素数据，加之其透镜组的排列也未严格校正，使得量测结果存在畸变差等光学缺陷，因此不能直接用于摄影测量像位的解算。为保证在摄影测量中非量测相机可提供较高的量测精度，需对相机各个参数进行精确检校。相机参数检校质量的高低直接关系着能否满足测量精度的要求，也直接影响非量测相机在摄影测量中的适用范围，所以开展非量测单相机检校的研究有着重要的实际意义。

非量测数码相机检校方法较多，一般在进行检校时应在检校场配备足够数量的控制点，但在缺乏控制点的情况下或有很高测绘精度要求时，则需根据实际情况选择适当的检校方法来满足具体测量的任务要求。本文所提方法不用配备高精度的控制场，且布置方便、造价低廉。通过在不同摄站以不同角度对目标进行摄影来获取多幅图像，并运用ERDAS对影像做预处理，可增强对比度及除噪目的，再提取类似棋盘检校场的标志点的像素坐标。由投影变换，推导视觉共线方程，构造同形矩阵。最后根据同形矩阵的约束条件，解算内方位元素以及外方位元素的初始值，联立多片后方交会最佳优化模型解算出相应的畸变参数，以及通过检验系统参数的显著性来确定该方法的有效性。

1倾斜相机的检校及影像获取过程

1.1　倾斜相机检校的内容

数字相机的检校内容包括测定主点位置(x0，y0)、主距(f)及光学畸变系数。光学畸变包括径向畸变、切向畸变及CCD面阵变形。本文主要分析径向畸变k1，k2，k3，切向畸变p1，p2。

1.2　检校场布置

为获取相机的内方位和畸变差，检校场布置应满足如下条件：

1) 标志点在三维空间上类似棋盘分布，拍摄相片时，标志点应覆盖整个像幅。

2) 标志点不可在一个平面上，需有一定的起伏。

检校建立了室外检校场,在某家属楼立面布设数百个间隔为1.5～2.5 m 的控制点标志。该楼高约30 m，宽约100 m，其墙体有电梯、走廊和凹槽，且构成前后4个层次的立体结构。控制点标志是由黑色铝片制成。为了提高控制点坐标的获取效率，在铝片中间粘贴了全站仪棱镜反光片，如图1所示。

图1　检校场实景图以及检校场控制点样式

1.3　影像获取原则

1)正交旋转拍摄，应有相互垂直拍摄的相片，实际拍摄时有多种旋转方式；

2)拍摄的摄影光束需满足几何收敛性条件，如图2所示。理想情况下，摄影光线的最大交会角在70°～100°范围内；

3)如图3所示，拍摄的基线B与摄站到检校场的垂直距H的基高比大约在1.2~1.5，可满足较好的几何收敛条件。

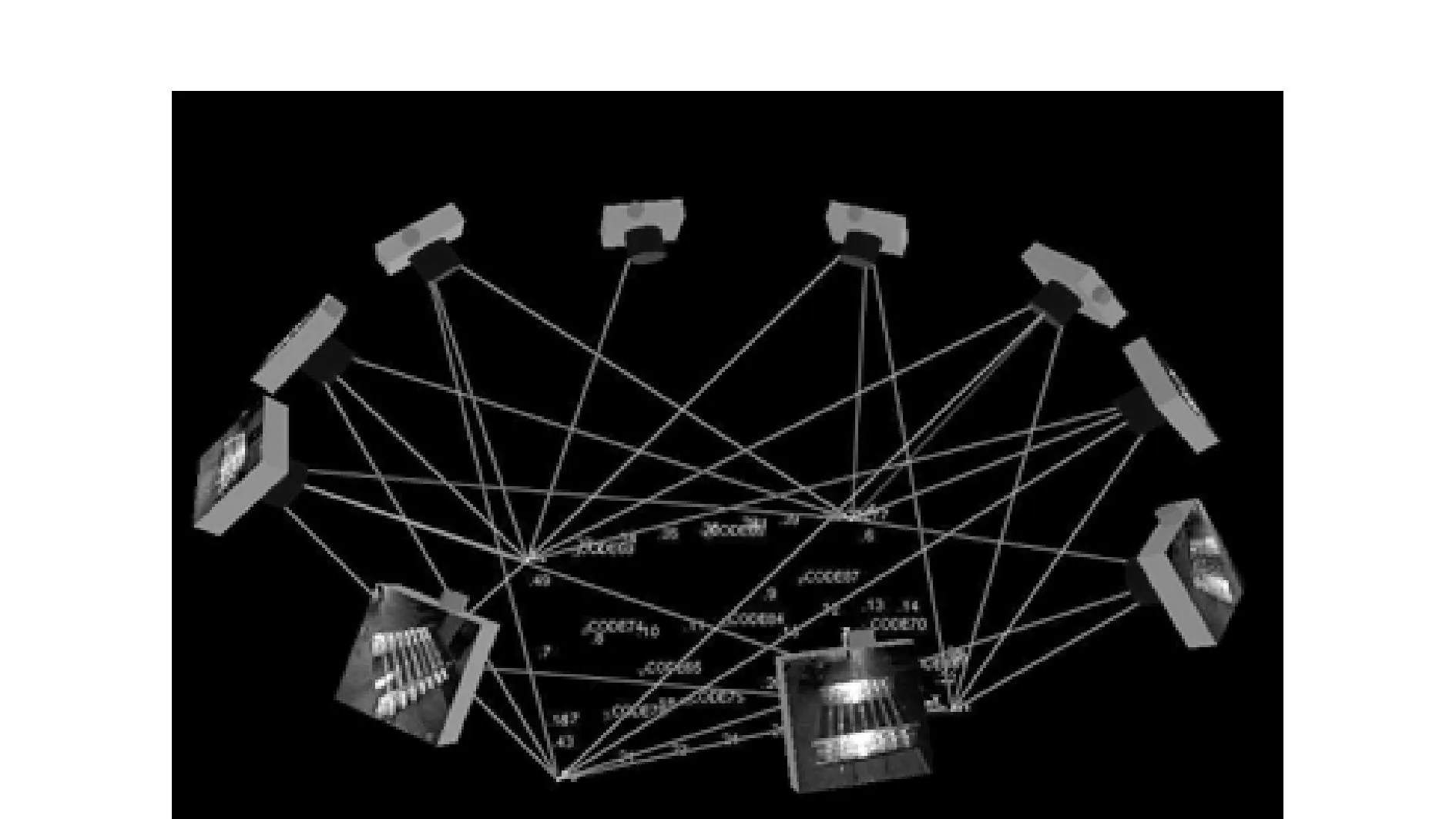
图2　几何收敛性条件

图3　摄站示意图

2倾斜相机检校原理

2.1　求解内、外方位元素的初始值

由于3D和2D检校场都会涉及到内方位元素及其外方位元素初值问题，因此本文根据检校场的特性，建立视觉共线方程以及同形矩阵的约束条件来解决初值问题。

2.1.1　求解内方位元素初始值

由投影变换，推导出视觉中共线方程为

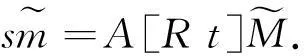
(1)

其中：

式中：α0=fx，β=fy，μ0=x0，v0=y0，s为像素分辨率，γ为x与y轴不垂直度，R为旋转矩阵。XS，YS，ZS为外方位元素的直线元素。

对于平面，Z=0，有

(2)

假设H为3阶同形矩阵，则令

(3)

由共线方程和二维DLT之间的关系导出下列表达式：

(4)

消去λ后，n个点可以列2n个误差方程，求9个未知数的齐次方程，然后按奇异值分解方法求解，取特征值最小的解。设B2n×9为误差方程系数，于是误差方程为

(5)

奇异方程求解

(6)

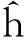
为了求解内方位元素的初始值，则需构造同形矩阵的两个约束条件。其表达式为

(7)

由旋转矩阵正交性质可知，自身列模等于1，相邻向量垂直且乘积等于0，即

(8)

将式(7)代入式(8)得

(9)

假设矩阵K3×3为对称矩阵，则可得

(10)

将对角矩阵K代入式(9)，可得

(11)

在同形矩阵的约束条件下，基于每张影像可列两个方程。因有5个参数，则至少需要3张相片。同理，采用奇异值分解法求解，求其最小特征对应的特征向量为内方位元素函数的初始值。结合以上函数关系，可解算出所需的内方位元素初始值。

2.1.2　求解外方位元素初始值

通过上述分析，求解出内方位元素构成的同形矩阵，那么根据式(7)求解出像方与物方旋转矩阵的r1，r2。又旋转矩阵满足右手定则，则有

(12)

联立式(7)和式(12)，可求解角元素的初始值，然后利用式(1)，便可得到相应直线元素的初始值。

2.2　多片后方交会的优化模型

2.2.1　初次优化

在已经求解出的内方位元素以及外方位元素的基础上，根据后方交会原理，对每张相片的内方位元素以及外方位元素实施再次优化。其表达式为

(13)

式中：A，Ri，ti分别为第i张影像的内方位元素、角元素、直线元素的初步优化值，Mj为第i张影像上的像点j的物方坐标。

2.2.2　最佳优化

由于相机存在光学畸变，所以最佳优化目的是采用多片倾斜影像的后方交会原理解算径向畸变与切向畸变。其表达式为

(14)

式中k1，k2，k3，p1，p2分别为3个径向畸变参数，2个切向畸变参数。

2.3　系统参数的检校

多片后方交会的最佳优化模型的误差方程为

(15)

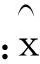
在相机检校中，经常无法确定畸变参数的中误差，于是根据经验可知畸变参数的期望为0，于是可采用t检验法。

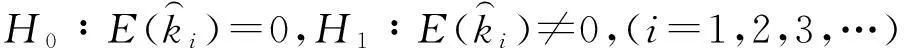
(16)

若|t(f)|

值一致，否则就认为两者有显著差别，同理切向畸变参数也类似检验。

3实例分析

在该实验中，为满足几何收敛条件，选择检校场对面的楼顶和地面作为拍摄地点，可以得到满足较高精度的交会角。两楼间的距离大约40 m，相对于焦距满足调焦到无穷远的条件。拍摄所在楼顶大约长60 m，从楼顶一边到另一边连续拍摄，基高比为1.5，即满足几何收敛条件。采用旋转拍摄方式，则可以得到相互倾斜拍摄的相片(见图4)。

图4　不同旋转角度拍摄的影像图片

3.1　数据处理

选取拍摄影像，利用ERDAS软件进行增强对比度、去噪等处理后，分别提取每张影像5个相邻标志点的像素坐标(像素单位为0.006 mm)和记录对应点的物方坐标。通过VC++程序设计对提取的数据文件进行处理,计算流程如图5所示。

对于3张影像标志点提取的像点坐标以及物方坐标，如表1所示(1pixel=0.006 mm)。

图5　影像数据计算流程

表1　测量数据

通过VC++程序设计对上述数据进行处理后，得到数据见表2。

表2　棋盘法求解的畸变参数

表中α为fx，β为fy，μ0为x0，v0为y0。k1，k2，k3为径向畸变差，p1，p2为切向畸变差。

为验证该方法的有效性，则采用传统直线性变

化换法对上述数据进行解算，得到畸变参数结果见表3。

表3　直线性变换法求解的畸变参数

3.2　系统参数的t检校

该实验选用15个标志点的坐标，共列30个误差方程。其中每张相片有6个外方位元素，共用相同的内方位元素，因此共有27个必要参数元素，且自由度f=3。

表4　畸变参数检校比较

由表4表明：由于t(k3)=3.212 4>3.182,故其拒绝H0，而其他检校参数都接受H0。因此对于只考虑2个径向畸变参数的相机检校，该方法是适用的。然而直线性变换法求解的畸变参数k10，k20，p10，p20的值都拒绝H0，仅有k30接受H0。结合表2、表3与表4及t检校结果得出以下结论：

1) 用直线变换解算的畸变参数的中误差都比该算法解算的畸变参数小，但直线变换检校参数都拒绝t检校的原假设。因此中误差不是唯一能准确评定精度的指标。 尤其引入系统参数时， 原平差模

型发生变化。

2) 通过比较分析，该算法可用于相机检校，且比直线线性变换的效率更高，迭代次数少，明显提高计算速度。

4结束语

本文利用基于类似棋盘检校场的数字相机检校方法进行相机检校，可达到预期目的，明显比传统方法的检校效率高。例如该方法未采用昂贵的

三维场，可通过布置简单的标志点，在检校场进行检校。经实验分析，基于类似棋盘检校场中的数字相机检校方法也存在一些问题：①数据噪声的处理，若求解奇异方程组时，利用高斯求解不能正确处理数据噪声。当角线元素特别小，其数据噪声较大，无法求得理想解。②虽可达到预期目的，但其中某些参数不接受假设条件，需分析其原因或改善函数模型。③该方法能否在任意检校场得到推广及应用，还需继续试验与验证。笔者将继续关注这一领域的发展，做更多的尝试，完善上述分析。

参考文献：

[1]冯文灏.近景摄影测量[M].武汉:武汉大学出版社,2002.

[2]冯文灏.关于近景摄影检校的几个问题[J].测绘科学,2000,25(10):10-13.

[3]张祖勋,张剑清.数字摄影测量学[M].武汉:武汉测绘科技大学出版社,1997.

[4]崔红霞,孙杰,林宗坚，等.非量测数码相机的畸变差检测研究[J].测绘科学,2005,30(1):105-107.

[5]李德仁,王新华.CCD阵列相机的几何标定[J].武汉测绘科技大学学报,1997,22(4):308-313.

[6]王之卓.摄影测量原理[M].武汉:武汉大学出版社,2007.

[7]陈铮.三相机结构光摄影测量中人工标志同名像点自动匹配方法[J].测绘工程,2013,22(1):28-31.

[8]喻夏琼,高岩.基于非线性优化的摄像机2D标定法[J].测绘工程,2013,22(5):25-29.

[9]刘晨，耿娟，贺一楠，等.极坐标法在非量测相机检校场控制测量中的应用[J].测绘工程，2014，23(10)：50-53.

[10]陈铮，黄桂平，冯欣，等.三相机结构光摄影测量中人工标志同名像点自动匹配方法[J].测绘工程，2013，22(1)：28-30.文灏.近景摄影测量[M].武汉:武汉大学出版社,2002.

[2]冯文灏.关于近景摄影检校的几个问题[J].测绘科学,2000,25(10):10-13.

[3]张祖勋,张剑清.数字摄影测量学[M].武汉:武汉测绘科技大学出版社,1997.

[4]崔红霞,孙杰,林宗坚，等.非量测数码相机的畸变差检测研究[J].测绘科学,2005,30(1):105-107.

[5]李德仁,王新华.CCD阵列相机的几何标定[J].武汉测绘科技大学学报,1997,22(4):308-313.

[6]王之卓.摄影测量原理[M].武汉:武汉大学出版社,2007.

[7]陈铮.三相机结构光摄影测量中人工标志同名像点自动匹配方法[J].测绘工程,2013,22(1):28-31.

[8]喻夏琼,高岩.基于非线性优化的摄像机2D标定法[J].测绘工程,2013,22(5):25-29.

[9]刘晨，耿娟，贺一楠，等.极坐标法在非量测相机检校场控制测量中的应用[J].测绘工程，2014，23(10)：50-53.

[10]陈铮，黄桂平，冯欣，等.三相机结构光摄影测量中人工标志同名像点自动匹配方法[J].测绘工程，2013，22(1)：28-30.

[责任编辑：刘文霞]

中图分类号：TP79

文献标志码：A

文章编号：1006-7949(2015)02-0055-05

收稿日期：2014-02-20；修回日期：2014-12-15

作者简介：张阳阳(1987-)，女，助教.

The check method of digital camera calibration based on chessboard check-like drill ground
ZHANG Yang-yang1,MEN Lin-jie2,ZHOU Gui-chu3,YANG Juan3
(1.Scholl of Resource and Environmental Sciences,Gansu Agricultural University,Lanzhou 730070,China;2.Gansu Institute of Land Resources Planning,Lanzhou 730000,China;3.School of Information Engineering,China University of Geosciences,Wuhan 430074,China)

Abstract：For many non-measured single camera calibration methods,a method of inclined camera calibration based on chessboard check-like drill ground is proposed.The method uses the relationship of between collinear equation and the two-dimensional DTL to deduce the lord ordinate equation including nine parameters of the two-dimensional DTL by constructing the homomorphism matrix，and gets the initial value of internal and exterior orientation elements through the different exposure station with shooting more target images.At the last，the method solves the camera check parameters with many images of the space resection，and tests the significance of camera system parameters.

Key words：inside orientation elements；exterior orientation elements；distortion parameters；isomorphism matrix；system parameter