ABAQUS中混凝土塑性损伤因子的合理取值研究

田连波，侯建国

（武汉大学土木建筑工程学院，湖北 武汉 430072）

0 引言

ABAQUS是国际上最先进的大型通用有限元软件之一，可以分析复杂的工程力学问题.ABAQUS使用说明中对混凝土塑性损伤模型的参数取值做了比较详细的说明，但关于混凝土塑性损伤因子如何取值则不详［1］.我国现行《混凝土结构设计规范》（GB 50010-2010）附录C.2给出混凝土塑性损伤因子取值的计算公式［2］，但按该公式计算的塑性损伤因子无法满足ABAQUS对数据的检验要求，导致出错提示.目前国内外关于混凝土塑性损伤演化方程的推导一般采用两种等效性假设，一种是应变等效性假设，由Lemaitre于1971年提出，损伤单元在应力σ作用下的应变响应与未受损伤单元在有效应力σˉ作用下的应变响应相同，在外力作用下，损伤单元的材料本构关系可采用未受损伤单元的材料本构关系，只需将其中的应力简单地换成有效应力即可.文献［3-4］基于应变等效性假设，结合《混凝土结构设计规范》（GB 50010-2010）建议的单轴本构关系，推导出塑性损伤因子的计算公式.另一种是能量等效性假设，Sidiroff提出应力作用在受损伤材料产生的弹性余能与作用在未受损伤材料产生的弹性余能在形式上相同，只需将应力改为等效应力，或将弹性模量改为损伤时的等效弹性模量即可［5-6］.本文中基于能量等效性假设，给出混凝土塑性损伤因子取值的计算方法.根据本文中建议方法确定的混凝土塑性损伤因子取值，利用ABAQUS软件，对钢次梁插入式节点的混凝土框架梁试验模型进行非线性全过程分析，有限元分析结果与试验结果吻合较好.

1 ABAQUS塑性损伤模型

1.1 ABAQUS塑性损伤模型 混凝土在承受外荷载前已有的微裂缝、微孔洞等被称为“损伤”，其破坏过程是各种尺度的损伤（微裂缝、微孔洞等）的发展演化和累积造成的，混凝土的非线性应力-应变特性主要由微裂缝的产生和集结引起.混凝土既有刚度退化又有塑性变形的存在，在细观物理机制上表现为既存在微裂缝、微缺陷的扩展，又存在与具体材料变形细观机理相联系的滑移与流动，合理的本构关系应为可以反映弹性损伤和塑性变形两种机制的弹塑性损伤本构模型.为了避免陷入分析材料微细结构的麻烦之中，一般都认为混凝土为宏观各向同性材料而对它的变形和失效机理进行研究.

ABAQUS的混凝土塑性损伤模型在Lubliner［7］、Lee and Fenves［8］模型的基础上建立.混凝土塑性损伤模型采用各向同性弹性损伤模型并结合各向同性受拉或受压塑性来模拟混凝土的非弹性行为.它基于各向有相同破坏的假设，适用于混凝土在任意荷载情况下的受力，包括循环荷载，同时考虑了由于拉、压塑性应变导致的弹性刚度的退化以及循环荷载作用下的刚度恢复.

在弹性阶段，混凝土塑性损伤模型（concrete damaged plasticity model，简称CDP模型）采用弹性模型对材料的力学性能进行描述，进入损伤阶段后，CDP模型损伤后的弹性模量的关系式为，

式中，E0为初始弹性模量，d表示拉伸或压缩时的塑性损伤因子dt或dc.塑性损伤因子d的取值范围为0～1，0表示材料未出现损伤，1表示材料强度的完全丧失.

1.2 ABAQUS中受拉损伤的应力-应变关系 ABAQUS中超出弹性部分的受拉应力-应变曲线数据以的形式输入，受拉开裂应变定义为总应变减去材料无损时的弹性应变，如图1所示.

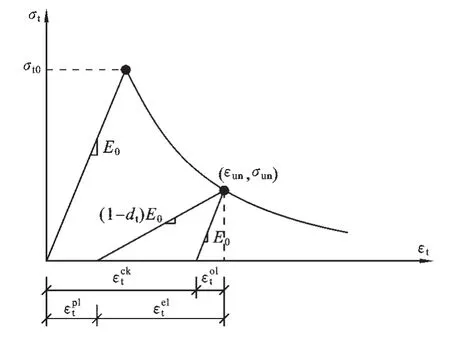
图1 混凝土损伤塑性模型受拉应力-应变曲线

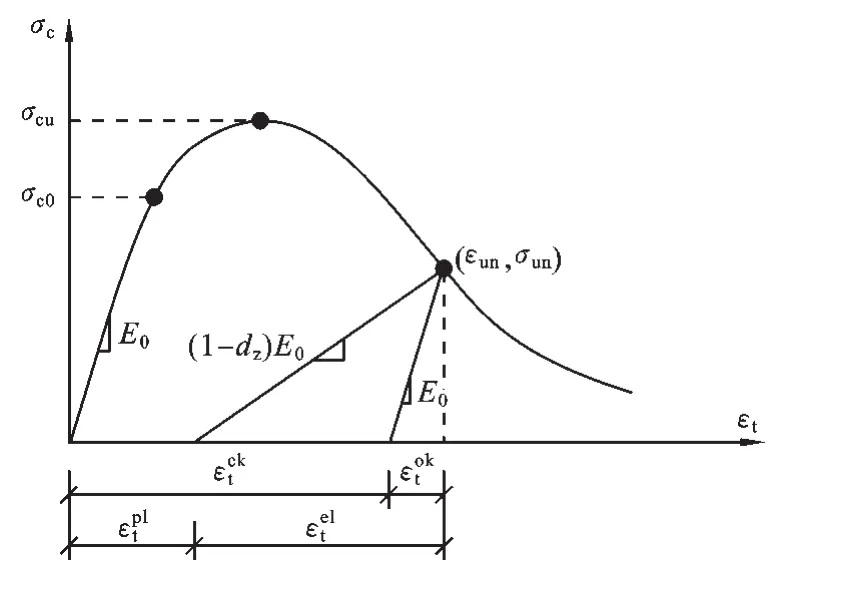
图2 混凝土损伤塑性模型受压应力-应变曲线

图1中，εun，σun——分别为卸载点的应变和应力；

1.3 ABAQUS中受压损伤的应力-应变关系 ABAQUS中超出弹性部分的受压应力-应变曲线数据以的形式输入，受压非弹性应变定义为总应变减去材料无损时的弹性应变，如图2所示.

图2中，εun，σun——分别为卸载点的应变和应力；

2 塑性损伤模型塑性损伤因子计算公式的推导

2.1 混凝土单轴本构模型 采用ABAQUS损伤塑性模型进行计算时，需要用户分别输入材料的受压、受拉应力-非弹性应变曲线，以及材料受压、受拉时塑性损伤因子-非弹性应变曲线.对于描述模型弹性阶段的杨氏模量E0的取值问题，考虑到CDP模型采用的是等向强化模型，根据文献［2］提供的混凝土本构关系，取混凝土受拉开裂时的割线模量作为混凝土的初始弹性模量，即本文中以C40混凝土为例，式（4）、式（5）通过文献［2］提供的混凝土本构关系简化而来，能满足大体积混凝土结构的基本要求.

2.2 简化后的混凝土单轴本构模型

2.2.1 简化后的混凝土单轴受拉应力-应变曲线 混凝土单轴受拉的应力-应变曲线方程可按公式（4）确定，在计算中前半部分取为线弹性，损伤只发生在峰值后.混凝土单轴受拉的应力-应变曲线如图3所示.

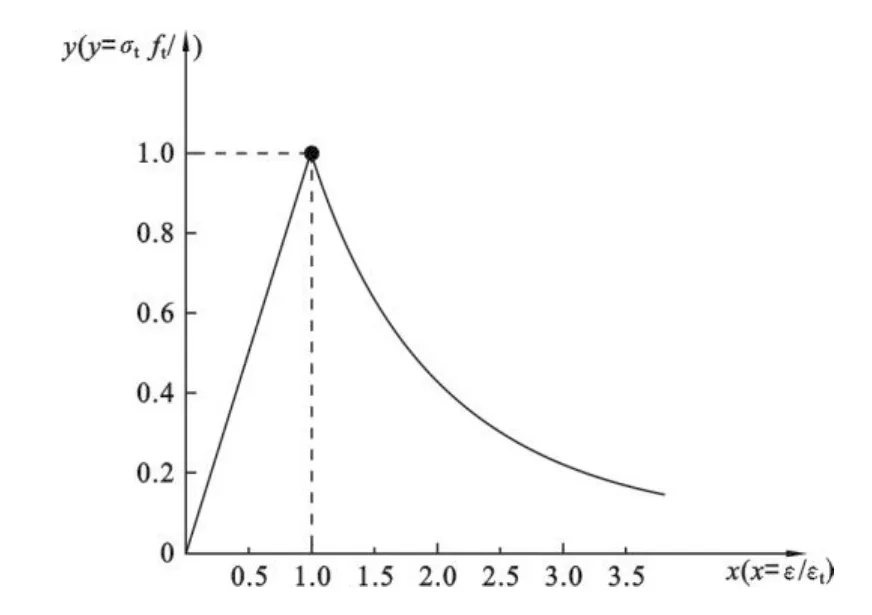
图3 混凝土拉伸应力-应变曲线

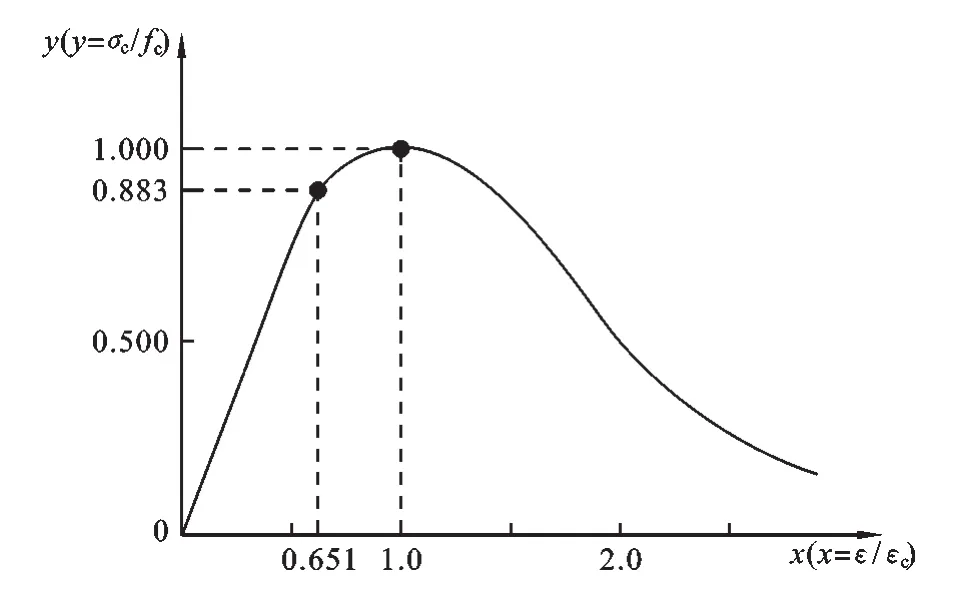
图4 混凝土压缩应力-应变曲线

2.2.2 简化后的混凝土单轴受压应力-应变曲线 根据文献［2］中提供的混凝土单轴受压应力-应变曲线计算出上升段割线模量等于混凝土受拉开裂时对应的割线模量E0的点，此应力点之前取为线弹性，损伤发生在此应力点之后.本文中以C40为例，在受压应力-应变曲线上逐步进行插值，刚好在所对应点的割线模量为E0.混凝土单轴受压的应力-应变曲线方程可按公式（5）确定，计算中在x≤0.651部分取为线弹性，在x＞0.651后开始发生损伤.混凝土单轴受压的应力-应变曲线如图4所示.

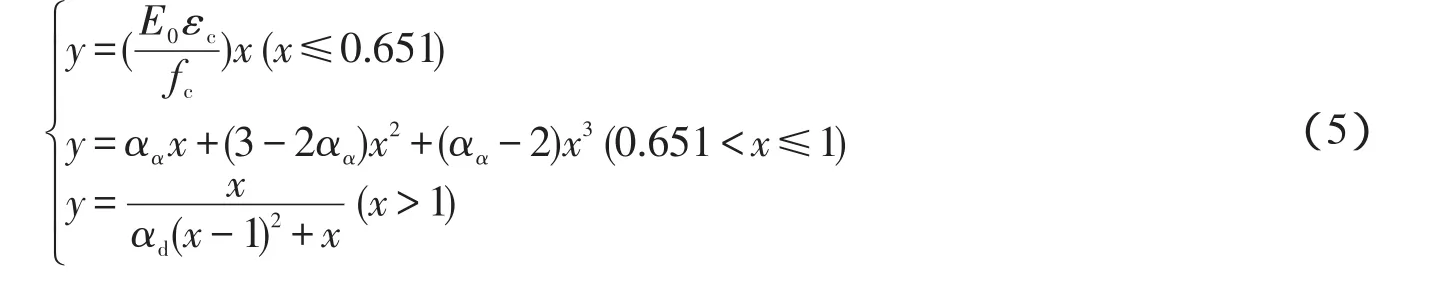
公式（5）中，

ft——混凝土的单轴抗拉强度；

εt——与 ft相应的混凝土峰值拉应变；

αt——单轴受拉应力-应变曲线下降段的参数值，计算见文献［2］附录C.2.1；

fc——混凝土的单轴抗压强度；

εc——与 fc相应的混凝土峰值拉应变；

αa、αd——分别为单轴受压应力-应变曲线上升段和下降段的参数值，计算见文献［2］附录C.2.1.

2.3 混凝土塑性损伤因子的计算公式 根据Sidoroff的能量等价原理，应力作用在受损材料产生的弹性余能与作用在无损材料产生的弹性余能在形式上相同，只需将应力替换为等效应力，或是将弹性模量替换为损伤时的弹性模量.

通过公式（6）～公式（8），得Ed=E0(1-d)2，则可以得到应力与应变的关系：

单轴受拉塑性损伤因子dt的计算公式如下：

单轴受压塑性损伤因子dc的计算公式如下：

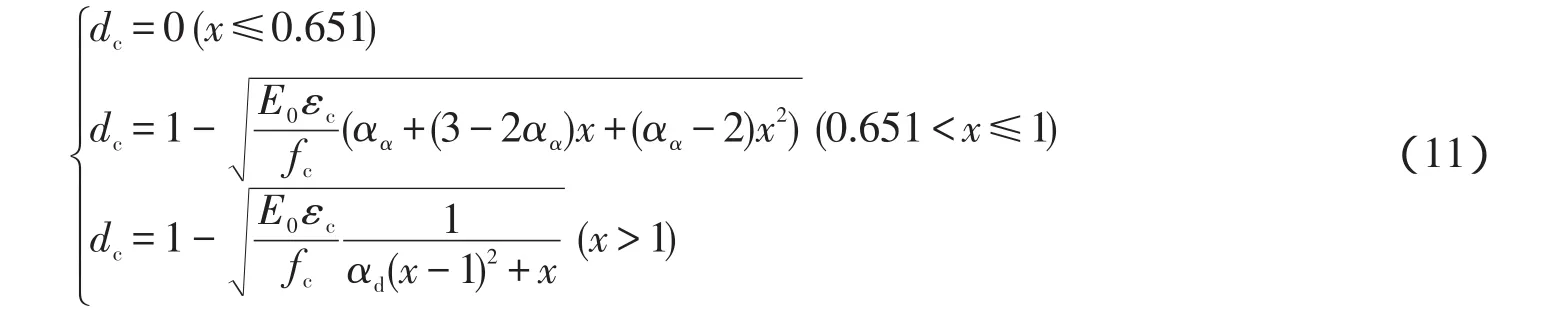
其中，αt——单轴受拉应力-应变曲线下降段的参数值，计算见文献［2］附录C.2.1；

αa、αd——分别为单轴受压应力-应变曲线上升段和下降段的参数值，计算见文献［2］附录C.2.1.

3 钢次梁插入式节点的混凝土框架梁试验模型非线性有限元分析

3.1 有限元模型 钢次梁插入式节点的混凝土框架梁试验基于某一火力发电厂实际工程，采用1∶2缩尺模型，试验模型为从楼面结构中截取一根混凝土主梁为研究对象.对于钢次梁插入式节点模型，混凝土框架主梁截面尺寸为b×h=300 mm×800 mm，跨度为5.0 m；柱子截面尺寸为b×h=400 mm×800 mm，高度为1.3 m；连系梁截面尺寸为b×h=300 mm×400 mm，长度为1.2 m.在每根框架主梁同一侧单边插入3根钢次梁，钢次梁间距为1.25 m.模型的钢次梁为HN400×200，插入混凝土主梁的深度取为200 mm，外伸长度取210 mm，钢次梁总长为410 mm.混凝土采用八节点减缩积分单元格式的三维实体单元(C3D8R)模拟，钢次梁用四节点曲壳单元(S4R)模拟，钢筋用两节点线性三维桁架单元(T3D2)模拟，钢筋和钢次梁与混凝土的接触面作用均用emdedded方式处理［9-11］.试验模型布置见图5.

3.2 计算参数 本文中提出的塑性损伤因子的计算方法所需要的参数为混凝土受压强度及受拉强度.以C40混凝土为例，轴心抗压强度标准值26.8 N/mm2，轴心抗拉强度标准值 ftk=2.39 N/mm2，混凝土弹性阶段的杨氏模量E0取混凝土开裂时的割线模量作为混凝土的初始弹性模量，E0为22.9×105N/mm2，泊松比为0.2，材料进入塑性后，利用式（10）及式（11）求得CDP模型的塑性损伤因子，见表1.钢材采用Von Mises屈服准则及双线性弹塑性随动强化本构模型.

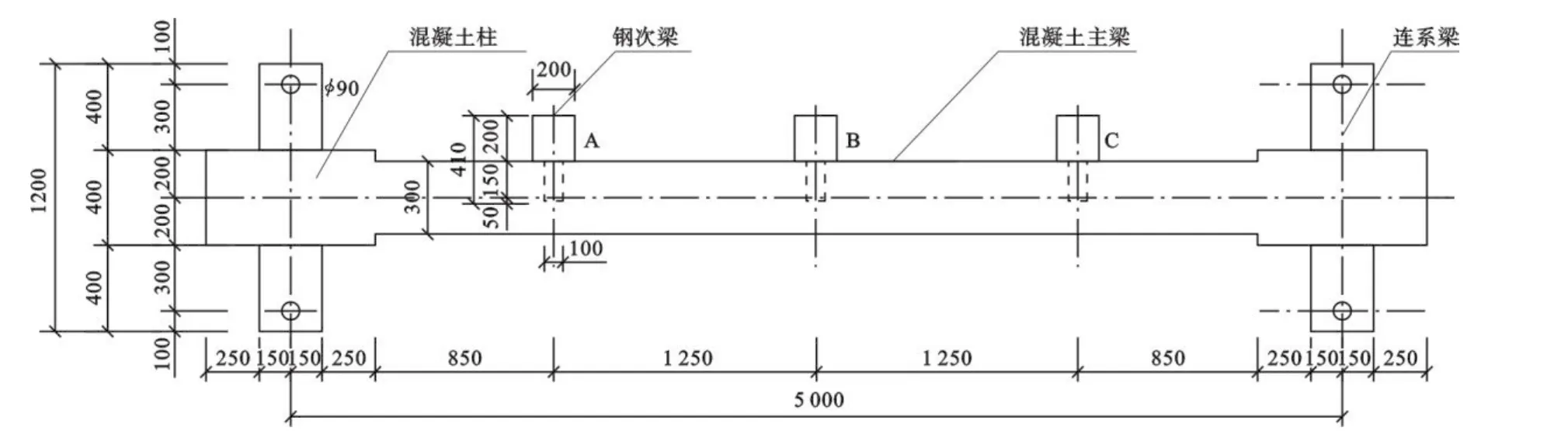
图5 模型的钢次梁HN400×200布置平面图

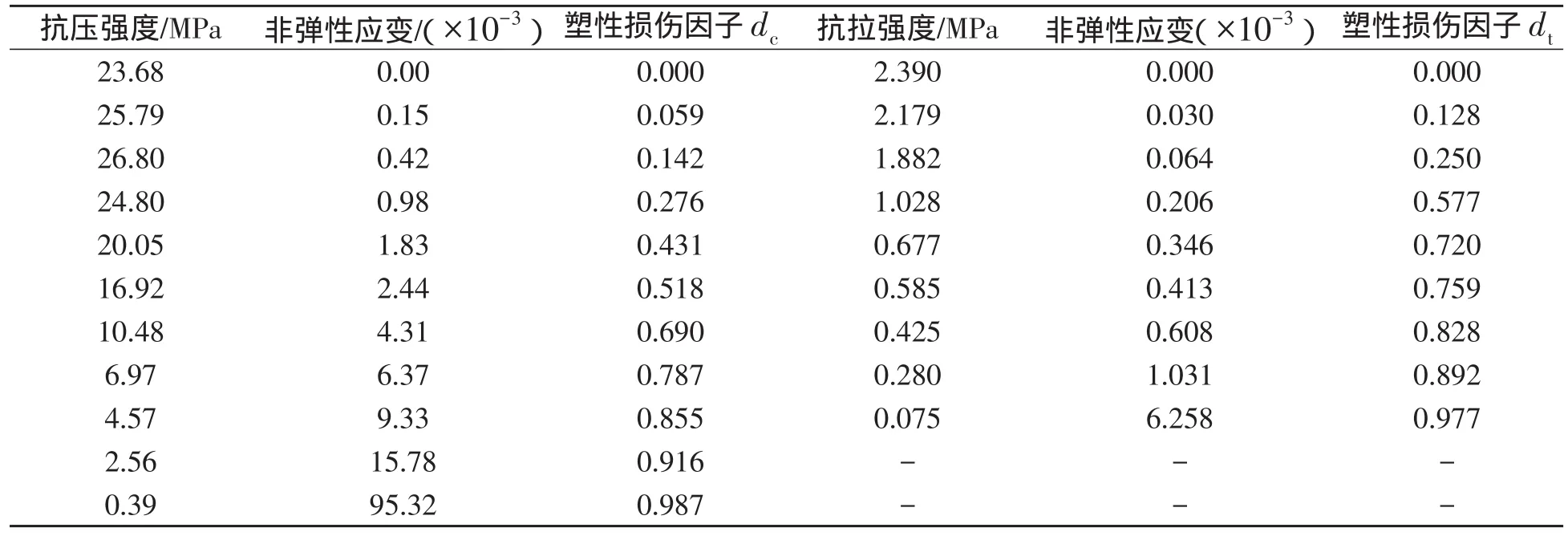
表1 C40混凝土计算参数

3.3 有限元分析结果与试验结果的对比分析 ABAQUS主要模拟了在间接荷载作用下插入式钢次梁混凝土框架梁的受力性能，节点A与节点C对称，所以只给出节点A和节点B加载时混凝土框架梁加载点的荷载-位移曲线与试验结果的对比，如图6所示.从图6可以看出，各模型的主梁混凝土开裂前，主梁加载点处的挠度计算值与模型试验值相近，说明在弹性阶段，有限元分析结果可以较好地反映试验模型的受力性能；主梁混凝土开裂后，主梁对应加载节点处的挠度计算值小于模型试验值，可能是由于模型试验时，是将某一钢次梁插入式节点加载至破坏后卸载至零，然后对另一钢次梁插入式节点进行加载试验，此时主梁是在已有混凝土裂缝的基础上进行加载试验，由于已有裂缝的影响，主梁的刚度会有所降低，而有限元分析时各节点的加载均是从零应力状态开始加载，有限元分析时主梁的刚度大于模型试验时的主梁刚度，使得有限元分析时主梁的挠度计算值比模型试验值偏小一些，但总体变化趋势是一致的.

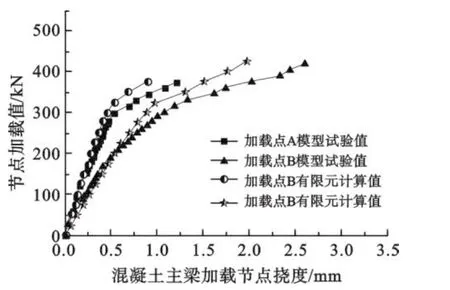
图6 模型加载点处主梁荷载-挠度曲线的有限元计算值与模型试验值的比较

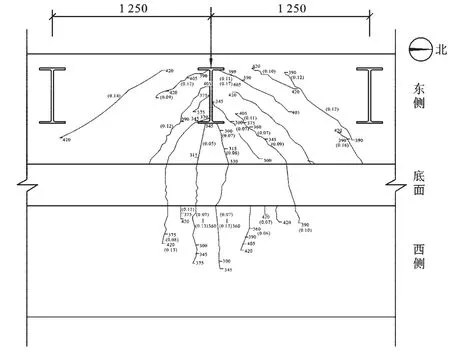
图7 模型节点B加载时混凝土主梁裂缝展开图

图7为模型试验的混凝土框架梁的破坏区域及开裂范围.图8为有限元模型的混凝土框架梁的受损情况，这与试验测得的结果规律是一致的.有限元分析时，模型将钢筋应变达到10 000με所对应的荷载定为破坏荷载，根据上述承载力极限状态标志，由有限元分析结果可确定模型的破坏荷载如表2所示.由表2可以看出，模型破坏荷载的有限元计算值与模型试验值的比值的平均值为1.003，变异系数为0.076，进一步验证了有限元分析结果的可靠性.有限元分析结果可证明上述推导的确定CDP模型的塑性损伤因子的计算方法是正确的，可以很好地模拟构件的破坏形态和骨架曲线.

图8 模型节点B加载时混凝土主梁塑性损伤因子分布图

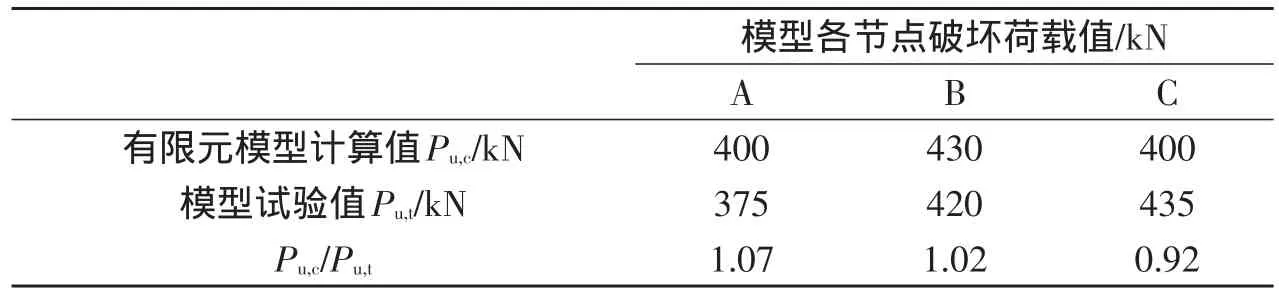
表2 模型破坏荷载的有限元计算值与模型试验值的比较

4 结论

通过CDP模型与《混凝土结构设计规范》（GB 50010-2010）中所给的混凝土单轴本构模型的对比分析，利用能量等价原理，推导CDP模型塑性损伤因子的计算方法，并对钢次梁插入式节点的混凝土框架梁试验模型进行非线性全过程分析，主要结论有：

1)本文中基于连续介质损伤力学，通过能量等价原理直接确定损伤因子，具有充分理论依据.

2)对混凝土结构设计规范所建议的单轴本构模型进行更合理的简化.以混凝土受拉开裂时的割线模量作为混凝土的初始弹性模量E0，并以此值为标准寻找单轴受压应力应变曲线上升段中割线模量等于E0的应力点，使得简化后的初始受拉弹性模量和初始受压弹性模量保持一致.

3)根据本文中确定的参数，其中塑性损伤因子随应变增长的变化规律能较好地模拟混凝土的刚度退化规律，可以进一步为分析混凝土构件的损伤行为提供数据和参考.对于复杂结构的非线性有限元分析也能较好地收敛.

4)该模型假定刚度损伤为各向同性，采用标量损伤因子d来描述，而实际上混凝土损伤为各向异性，故该模型无法精确描述各向异性的损伤情况，有待进一步研究.

［1］Hibbitt，Karlsson，Sorensen.ABAQUS/standard user subroutines reference manual［M］.USA:The Pennsylvania State University，1998:1-200.

［2］GB 50010-2010.混凝土结构设计规范［S］.北京：中国建筑工业出版社，2010.

［3］张劲，王庆扬，胡守营，等.ABAQUS混凝土损伤塑性模型参数验证［J］.建筑结构，2008，38（8）：127-130.

［4］张战廷，刘宇锋.ABAQUS中的混凝土塑性损伤模型［J］.建筑结构，2011，41：229-232.

［5］李兆霞.损伤力学及其应用［M］.北京：科学出版社，2002.

［6］刘新东，赫际平.连续介质力学［M］.北京：国防工业出版社，2011.

［7］Lubliner J，Oliver J，Oller S，et al.A plastic damage model for concrete［J］.International Journal of Solids and Structures，1989，25(3)：229-326.

［8］Lee J，Fenves G L.Plastic damage model for cyclic loading of concrete structures［J］.Journal of Engineering Mechanics，1998，124(8)：892-900.

［9］王金昌，陈页开.ABAQUS在土木工程中的应用［M］.杭州：浙江大学出版社，2006.

［10］庄茁，张帆，岑松，等.ABAQUS非线性有限元分析与实例［M］.北京：科学出版社，2005.

［11］徐亚丰，张丽，白首晏，等.ABAQUS工程实例模拟分析及详解［M］.沈阳：辽宁教育出版社，2013.