无线传感器网络拓扑边界辨识算法*

顾 德，王继帅

(1.江南大学 自动化研究所，轻工过程先进控制教育部重点实验室，江苏 无锡214122;2.中国科学院 苏州生物医学工程技术研究所，江苏 苏州215163)

0 引 言

无线传感器网络(wireless sensor networks，WSNs)由大量低值节点以自组织的方式组成网络，十分适合应用于无人值守的情景。一些早期的研究成果常常假设WSNs 部署区域是一个凸区域，但实际应用中，如果部署区域内含有障碍物，不满足上述假设，则会使这些算法的表现达不到预期。因此，了解部署区域几何形状有利于优化WSNs 工作表现，将处在WSNs 边界的节点识别出来则是描述部署区域几何形状的最直观的方法。此外，拓扑边界是在复杂形状的WSNs 中判断网络拓扑瓶颈的必备条件［1］，也是进行近凸分块的必备条件［2，3］。

文献中有以下几类WSNs 边界辨识方法:

1)基于统计的方法:Fekete S 认为如果某个节点的邻节点数量显著少于其他节点，那么该节点就在边界位置［4］。但是此方法要求部署的密度达100 左右时，才能有合理的结果［5］。

2)基于拓扑的方法:Funke S 提出了一种在WSNs 中构造等距离线并通过判断等距离线的中断点来判断WSNs 边界的方法［6］。Wang Y［5］提出的方法在含有孔洞的WSNs内寻找到一部分边界后，将边界上的节点连接起来，以降低漏认率。Simek M［7］提出的方法也属此类，并且漏认率较低。但是以上方法都存在较高的误认率。

3)基于空间位置的方法:Fang Q 提出一种在WSNs 中沿某个确定的方向发送数据包，通过观察数据包最终停留的节点来判断边界［8，9］。但此方法要求节点具有位置感知能力。

本文认为，在辨识WSNs 边界时，应当优先抑制误认率，少数误认的边界就将影响对WSNs 的整体判断，而漏认少数边界节点并不影响大局，剩余的边界节点足以勾勒出WSNs 的分布范围。本文将在以下假设和限制下讨论完成WSNs 边界辨识的方法:1)本算法不依赖WSNs 节点位置感知能力;2)WSNs 节点均匀随机部署;3)短时间内，网络节点是静态的。

1 算法思想

在连续的标量场中，等值线的断开处必然在物体的边界上。例如:可以观察到在任何一个时刻，某国气象信息中的任意一条等温线，要么是闭合的曲线，要么是一条连接其国界线上两点的曲线段。所以，如果能在一个平面区域中构造一个连续的标量场，那么，寻找一个平面区域的边界的问题就可以转化为寻找曲线段的端点的问题。

1.1 构造连续标量场

在平面区域中构造连续标量场并不困难。例如:加热一个固体薄片的某几个点一段时间，这个固体中就会出现一个温度场。此后观察等温线，将等温线的端点标记出来，就可以获得该固体薄片的边界。

根据傅里叶定律，可以推导出该固体中任何一点的温度变化情况

其中，∂T/∂t 为该点温度随时间的变化率，λ，c，ρ 分别为热传导系数、热容、密度，Q 为单位时间内该点从系统外获得的热量。当该点为被加热点时，Q 为正值常数;否则，Q=0。

根据上述公式，可以用数学的方式推演热传导的过程，构造连续的标量场。

1.2 辨识等值线的端点

曲线的端点具有明显的特征，可根据以下条件判断:以曲线上一点为圆心，r 为半径作圆，当r→0 时，若圆与曲线只有一个交点，则圆心为曲线的端点。

这样，在构造连续标量场并判断出等值线的端点后，平面区域的边界就辨识出来了。

受到这种算法思想的启发，开发了一种新的辨识WSNs 边界的方法。

2 WSNs 边界辨识算法

2.1 热传导规律的离散化

将均匀随机部署的WSNs 节点视为构成固体的子块。如图1，若节点i 与n 个其他节点相邻，则视固体中的子块gi与n 个其他子块相邻。

将公式(1)从空间上离散化，可得

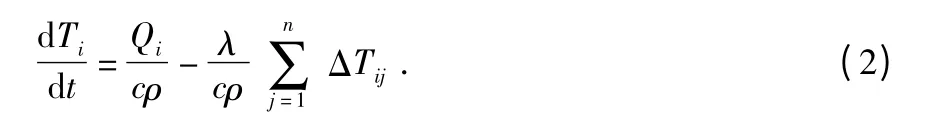
其中，ΔTij为gi与gj的温差。继续将公式(2)在时间上离散化，可得

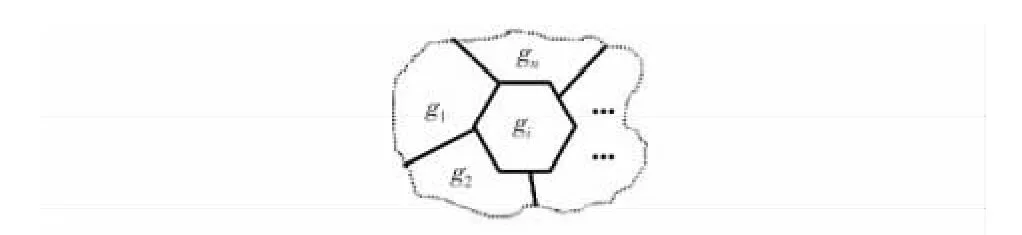
图1 gi 与n 个其他子块相邻Fig 1 gi surrounded by n other blocks

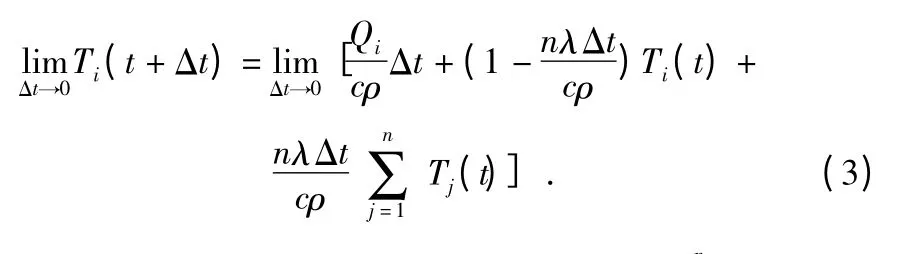
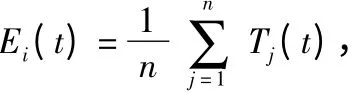
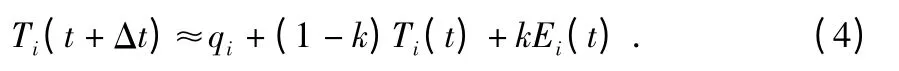
2.2 在WSNs 中构建虚拟温度场

在WSNs 中，随机地挑选若干个节点作为热源，赋予其一个正值的qi，然后按照式(4)描述的规律，在WSNs 中模拟热传导现象，反复进行一段时间之后，WSNs 中就构建起了虚拟的温度场。

2.3 建立虚拟等温线

在模拟热传导现象结束后，每个节点与其相邻节点交换虚拟温度值，选择虚拟温度值与其本身最为接近的若干节点作为自身的候选近似等温点，如果双方互相将对方选择为候选近似等温点，则确认该两个节点近似等温。在本文中选择候选节点的数量为其邻节点数量的30%。

在WSNs 整个网络的各个节点之间完成近似等温点的确认之后，网络中就建立了虚拟等温线，如图2 所示。图中，五角星表示被选为热源的节点，连线表示确认的近似等温线，线条表示了不同的温度值。

图2 虚拟等温线Fig 2 Virtual isotherm

2.4 确定等温线的端点

经过上一节的步骤，平面边界的辨识问题转换成了折线端点辨识问题。此时节点i 可以数出其等温邻节点数Ni，然后通过一次邻域内的广播，节点i 可以了解到处在同一条等温线上的相邻的其他节点的等温邻节点数，取其最小值，记为min Nneighbor。如果Ni≪min Nneighbor(在下文的仿真中，判断标准是Ni＜0.5min Nneighbor)，那么认为节点i 为等温线的端点，亦即WSNs 的边界节点，如图3 所示。从辨识结果看，等温线的端点基本上能够勾勒出整个区域的轮廓，并且很少有远离边界的误认点。

图3 等温线端点Fig 3 Endpoints of isotherm

3 仿真算例

图4 是几组仿真算例，将一些网络图案经二值化，以白色区域作为WSNs 的部署区域，边界形式包括圆弧、直线段、不规则曲线。有的算例是单连通的，有些算例是含有内部空洞。仿真结果表明:本算法能够适应各种不同的形状。

图4 仿真算例Fig 4 Simulated example

在以上算例中节点平均密度(平均每个节点拥有的邻节点数量)均在12 ～14 之间，在仿真测试中发现，降低节点密度会对本文提出的算法构成一定挑战，图5、图6 分别表现了当平均节点密度下降为10.9，8.9 时的辨识效果。

以上结果表明:本算法能适应的最低密度约为11 左右。

图5 平均密度为10.9Fig 5 Average density at 10.9

图6 平均密度为8.9Fig 6 Average density is 8.9

4 结 论

本文提出的算法是一种不依赖地理位置信息的分布式算法，具有较为广泛的应用价值。其方法上借鉴了自然现象中的规律，对于解决同类问题具有一定的参考价值。

本文所提出的方法也有一定的不足:从原理上来讲，加热一个固体，有可能出现等温线与物体的边界恰好完全重合，这种可能性是无法排除的。当出现某种特殊的情形时，可能会出现全局失效。因此，的确也存在虚拟等温线恰好与WSNs 边界完全重合的可能。目前尚无法排除这一可能，只能说，出现这种特殊情形出现的概率极低。

［1］ Gu D，Song C，Song Z.Bottleneck recognition by virtual temperature field in wireless sensor networks［J］.Ad－Hoc and Networks Wireless Sensor，2012，15(2－4):127－150.

［2］ Zhu X J，Sarkar R，Gao J.Segmenting a sensor field:Algorithms and applications in network design［J］.ACM Transactions on Sensor Networks(TOSN)，2009，5(2):1－32.

［3］ Gu D，Song Z.Segment and organize irregular shaped sensor networks by importing a virtual scalar field［C］∥IET International Conference on Wireless Sensor Networks，2010 IET－WSNs，2010:227－232.

［4］ Fekete S，Kröller A，Pfisterer D，et al.Algorithmic aspects of wireless sensor networks［M］.Berlin/Heidelberg:Springer，2004:123－136.

［5］ Wang Y，Gao J，Mitchell J S B.Boundary recognition in sensor networks by topological methods［C］∥Proceedings of the 12th Annual International Conference on Mobile Computing and Networking，2006:122－133.

［6］ Funke S.Topological hole detection in wireless sensor networks and its applications［C］∥Proceedings of the 2005 Joint Workshop on foundations of Mobile Computing(DIALM－POMC)，2005:44－53.

［7］ Simek M，Bocek J，Moravek P.Optimization of boundary recognition algorithms for wireless sensor networks applications［C］∥34th International Conference on Telecommunications and Signal Processing(TSP)，2011:189－194.

［8］ Fang Q，Gao J，Guibas L J.Locating and bypassing routing holes in sensor networks［C］∥23rd Annual Joint Conference of the IEEE Computer and Communications Societies(INFOCOM)，2004:2458－2468.

［9］ Fang Q，Gao J，Guibas L.Locating and bypassing holes in sensor networks［J］.Mobile Networks and Applications，2006，11(2):187－200.